Нелинейная регрессия

Регрессионный анализ

Подробности смотрите в кинетике Михаэлиса–Ментена.

В статистике нелинейная регрессия — это форма регрессионного анализа , в которой данные наблюдений моделируются функцией, которая является нелинейной комбинацией параметров модели и зависит от одной или нескольких независимых переменных. Данные подгоняются методом последовательных приближений (итераций).

Общий

В нелинейной регрессии статистическая модель вида:

${\displaystyle \mathbf {y} \sim f(\mathbf {x} ,{\boldsymbol {\beta }})}$

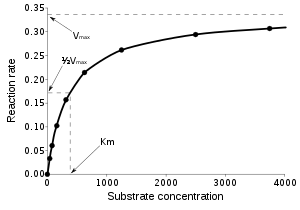
связывает вектор независимых переменных , , и его ассоциированные наблюдаемые зависимые переменные , . Функция нелинейна по компонентам вектора параметров , но в остальном произвольна. Например, модель Михаэлиса–Ментен для кинетики ферментов имеет два параметра и одну независимую переменную, связанные соотношением : ^[a] ${\displaystyle \mathbf {x} }$ ${\displaystyle \mathbf {y} }$ ${\displaystyle f}$ ${\displaystyle \beta }$ ${\displaystyle f}$

${\displaystyle f(x,{\boldsymbol {\beta }})={\frac {\beta _{1}x}{\beta _{2}+x}}}$

Эта функция, представляющая собой прямоугольную гиперболу, является нелинейной , поскольку ее нельзя выразить как линейную комбинацию двух s. ${\displaystyle \beta }$

Систематическая ошибка может присутствовать в независимых переменных, но ее обработка выходит за рамки регрессионного анализа. Если независимые переменные не свободны от ошибок, это модель с ошибками в переменных , также выходящая за рамки этого анализа.

Другие примеры нелинейных функций включают показательные функции , логарифмические функции , тригонометрические функции , степенные функции , гауссовы функции и распределения Лоренца . Некоторые функции, такие как показательные или логарифмические функции, можно преобразовать так, чтобы они стали линейными. При таком преобразовании можно выполнить стандартную линейную регрессию, но применять ее следует с осторожностью. Подробнее см. в разделе Линеаризация§Преобразование ниже.

В общем случае не существует замкнутого выражения для наиболее подходящих параметров, как в линейной регрессии . Обычно для определения наиболее подходящих параметров применяются алгоритмы численной оптимизации . Опять же, в отличие от линейной регрессии, может быть много локальных минимумов оптимизируемой функции, и даже глобальный минимум может давать смещенную оценку. На практике оценочные значения параметров используются в сочетании с алгоритмом оптимизации, чтобы попытаться найти глобальный минимум суммы квадратов.

Подробную информацию о нелинейном моделировании данных см. в разделах наименьшие квадраты и нелинейные наименьшие квадраты .

Статистика регрессии

Предположение, лежащее в основе этой процедуры, заключается в том, что модель может быть аппроксимирована линейной функцией, а именно рядом Тейлора первого порядка :

${\displaystyle f(x_{i},{\boldsymbol {\beta }})\approx f(x_{i},0)+\sum _{j}J_{ij}\beta _{j}}$

где — элементы матрицы Якоби. Из этого следует, что оценки наименьших квадратов определяются как ${\displaystyle J_{ij}={\frac {\partial f(x_{i},{\boldsymbol {\beta }})}{\partial \beta _{j}}}}$

${\displaystyle {\hat {\boldsymbol {\beta }}}\approx \mathbf {(J^{T}J)^{-1}J^{T}y} ,}$

сравнить обобщенные наименьшие квадраты с ковариационной матрицей, пропорциональной единичной матрице. Статистика нелинейной регрессии вычисляется и используется так же, как и в статистике линейной регрессии, но с использованием J вместо X в формулах.

Когда сама функция неизвестна аналитически, но ее необходимо линейно аппроксимировать с помощью или более известных значений (где — число оценщиков), наилучшая оценка получается непосредственно из линейной подгонки шаблона как ^[1] ​​(см. также линейный метод наименьших квадратов ). ${\displaystyle f(x_{i},{\boldsymbol {\beta }})}$ ${\displaystyle n+1}$ ${\displaystyle n}$ $${\displaystyle {\hat {\boldsymbol {\beta }}}=((\mathbf {Y{\tilde {M}}} )^{\mathsf {T}}{\boldsymbol {\Omega }}^{-1}\mathbf {Y{\tilde {M}}} )^{-1}(\mathbf {Y{\tilde {M}}} )^{\mathsf {T}}{\boldsymbol {\Omega }}^{-1}(\mathbf {d} -\mathbf {Y{\bar {m}})} }$$

Линейное приближение вносит смещение в статистику. Поэтому при интерпретации статистики, полученной из нелинейной модели, требуется большая осторожность, чем обычно.

Обычный и взвешенный метод наименьших квадратов

Часто предполагается, что наилучшая кривая — это та, которая минимизирует сумму квадратов остатков . Это подход обычных наименьших квадратов (OLS). Однако в случаях, когда зависимая переменная не имеет постоянной дисперсии или есть некоторые выбросы, сумма взвешенных квадратов остатков может быть минимизирована; см. взвешенные наименьшие квадраты . Каждый вес в идеале должен быть равен обратной величине дисперсии наблюдения или обратной величине зависимой переменной в некоторой степени в случае выброса ^[2] , но веса могут быть пересчитаны на каждой итерации в алгоритме итеративно взвешенных наименьших квадратов.

Линеаризация

Трансформация

Некоторые задачи нелинейной регрессии можно перенести в линейную область путем соответствующего преобразования формулировки модели.

Например, рассмотрим задачу нелинейной регрессии

${\displaystyle y=ae^{bx}U\,\!}$

с параметрами a и b и с мультипликативным членом ошибки U. Если мы возьмем логарифм обеих сторон, это станет

${\displaystyle \ln {(y)}=\ln {(a)}+bx+u,\,\!}$

где u = ln( U ), что предполагает оценку неизвестных параметров с помощью линейной регрессии ln( y ) на x , вычисление, которое не требует итеративной оптимизации. Однако использование нелинейного преобразования требует осторожности. Влияние значений данных изменится, как и структура ошибок модели и интерпретация любых выводимых результатов. Это могут быть нежелательные эффекты. С другой стороны, в зависимости от того, что является наибольшим источником ошибок, нелинейное преобразование может распределить ошибки по гауссову закону, поэтому выбор выполнения нелинейного преобразования должен быть обоснован соображениями моделирования.

Для кинетики Михаэлиса–Ментена линейный график Лайнуивера–Берка

${\displaystyle {\frac {1}{v}}={\frac {1}{V_{\max }}}+{\frac {K_{m}}{V_{\max }[S]}}}$

1/ v против 1/[ S ] часто использовался. Однако, поскольку он очень чувствителен к ошибкам в данных и сильно смещен в сторону подгонки данных в определенном диапазоне независимой переменной [ S ], его использование настоятельно не рекомендуется.

Для распределений ошибок, принадлежащих к экспоненциальному семейству , можно использовать функцию связи для преобразования параметров в рамках обобщенной линейной модели .

Сегментация

Урожайность горчицы и засоление почвы

Независимая или объясняющая переменная (например, X) может быть разделена на классы или сегменты, и линейная регрессия может быть выполнена для каждого сегмента. Сегментированная регрессия с анализом достоверности может дать результат, что зависимая или ответная переменная (например, Y) ведет себя по-разному в различных сегментах. ^[3]

На рисунке показано, что засоление почвы (X) изначально не оказывает никакого влияния на урожайность (Y) горчицы, пока не наступит критическое или пороговое значение ( точка разрыва ), после которого урожайность начинает ухудшаться. ^[4]

Смотрите также

• Математический портал

• Нелинейный метод наименьших квадратов
• Подгонка кривой
• Обобщенная линейная модель
• Локальная регрессия
• Методология моделирования реакции
• Генетическое программирование
• Программирование с несколькими выражениями
• Линейная или квадратичная подгонка шаблона

Ссылки

1. Britzger, Daniel (2022). "The Linear Template Fit". Eur. Phys. J. C. 82 ( 8): 731. arXiv : 2112.01548 . Bibcode : 2022EPJC...82..731B. doi : 10.1140/epjc/s10052-022-10581-w.
2. Motulsky, HJ; Ransnas, LA (1987). «Подгонка кривых к данным с использованием нелинейной регрессии: практический и нематематический обзор». Журнал FASEB . 1 (5): 365–374. doi : 10.1096/fasebj.1.5.3315805 . PMID  3315805.
3. RJOosterbaan, 1994, Анализ частоты и регрессии. В: HPRitzema (ред.), Принципы и применение дренажа, Опубл. 16, стр. 175-224, Международный институт мелиорации и улучшения земель (ILRI), Вагенинген, Нидерланды. ISBN 90-70754-33-9 . Скачать в формате PDF : [1] 
4. RJOosterbaan, 2002. Исследование дренажа на фермерских полях: анализ данных. Часть проекта «Liquid Gold» Международного института мелиорации и улучшения земель (ILRI), Вагенинген, Нидерланды. Загрузить в формате PDF: [2]. Рисунок был создан с помощью программы SegReg , которую можно бесплатно загрузить с [3]

Примечания

1. Эту модель можно также выразить в общепринятой биологической нотации:

   ${\displaystyle v={\frac {V_{\max }\ [{\mbox{S}}]}{K_{m}+[{\mbox{S}}]}}}$

Дальнейшее чтение

• Бетеа, Р.М.; Дюран, Б.С.; Бульон, Т.Л. (1985). Статистические методы для инженеров и ученых . Нью-Йорк: Марсель Деккер. ISBN 0-8247-7227-X.
• Мид, Н.; Ислам, Т. (1995). «Интервалы прогнозирования для прогнозов кривой роста». Журнал прогнозирования . 14 (5): 413–430. doi :10.1002/for.3980140502.
• Шитковски, К. (2002). Подгонка данных в динамических системах . Бостон: Клювер. ISBN 1402010796.
• Seber, GAF; Wild, CJ (1989). Нелинейная регрессия . Нью-Йорк: John Wiley and Sons. ISBN 0471617601.