Стандартная оценка

Сколько стандартных отклонений от среднего значения имеют наблюдаемые данные?

Сравнение различных методов оценки в нормальном распределении , включая: стандартные отклонения , кумулятивные проценты, процентильные эквиваленты, z-показатели, T-показатели.

В статистике стандартная оценка — это количество стандартных отклонений , на которые значение исходной оценки (т. е. наблюдаемое значение или точка данных) выше или ниже среднего значения того, что наблюдается или измеряется. Необработанные баллы выше среднего имеют положительные стандартные баллы, а те, которые ниже среднего, имеют отрицательные стандартные баллы.

Он рассчитывается путем вычитания среднего значения совокупности из индивидуального исходного балла и последующего деления разницы на стандартное отклонение совокупности . Этот процесс преобразования исходной оценки в стандартную оценку называется стандартизацией или нормализацией (однако «нормализация» может относиться ко многим типам отношений; дополнительную информацию см. в разделе «Нормализация» ).

Стандартные оценки чаще всего называются z -показателями ; эти два термина могут использоваться как взаимозаменяемые, как и в этой статье. Другие эквивалентные термины, используемые в физике высоких энергий, включают z-значение , z-статистику , нормальную оценку , стандартизированную переменную и притяжение . ^{[1] [2]}

Для расчета z-показателя требуется знание среднего и стандартного отклонения всей совокупности, к которой принадлежит точка данных; если у вас есть только выборка наблюдений из совокупности, то аналогичное вычисление с использованием выборочного среднего и выборочного стандартного отклонения дает t -статистику .

Расчет

Если известно среднее значение генеральной совокупности и стандартное отклонение генеральной совокупности, необработанный балл x преобразуется в стандартный балл с помощью ^[3]

${\displaystyle z={x-\mu \over \sigma }}$

где:

μ — среднее значение генеральной совокупности,

σ — стандартное отклонение генеральной совокупности.

Абсолютное значение z представляет собой расстояние между этим исходным показателем x и средним значением генеральной совокупности в единицах стандартного отклонения. z является отрицательным, когда исходный балл ниже среднего, и положительным, когда выше среднего.

Для расчета z с использованием этой формулы необходимо использовать среднее значение генеральной совокупности и стандартное отклонение генеральной совокупности, а не выборочное среднее или выборочное отклонение. Однако знание истинного среднего значения и стандартного отклонения популяции часто является нереалистичным ожиданием, за исключением таких случаев, как стандартизированное тестирование , когда измеряется вся совокупность.

Когда среднее значение генеральной совокупности и стандартное отклонение генеральной совокупности неизвестны, стандартный балл можно оценить, используя выборочное среднее значение и стандартное отклонение выборки в качестве оценок значений генеральной совокупности. ^{[4] [5] [6] [7]}

В этих случаях z -показатель определяется выражением

${\displaystyle z={x-{\bar {x}} \over S}}$

где:

${\displaystyle {\bar {x}}}$среднее значение выборки ,

S — стандартное отклонение выборки.

Хотя это всегда следует констатировать, различие между использованием статистики генеральной совокупности и выборочной статистики часто не проводится. В любом случае числитель и знаменатель уравнений имеют одинаковые единицы измерения, так что единицы сокращаются при делении, а z остается безразмерной величиной .

Приложения

Z-тест

Z-показатель часто используется в z-тесте стандартизированного тестирования – аналоге t-критерия Стьюдента для популяции, параметры которой известны, а не оцениваются. Поскольку знание всей совокупности очень необычно, t-критерий используется гораздо более широко.

Интервалы прогнозирования

Стандартную оценку можно использовать при расчете интервалов прогнозирования . Интервал прогнозирования [ L , U ], состоящий из нижней конечной точки, обозначенной L , и верхней конечной точки, обозначенной U , представляет собой интервал, в котором будущее наблюдение X будет лежать в интервале с высокой вероятностью , т.е. ${\displaystyle \gamma }$

${\displaystyle P(L<X<U)=\gamma ,}$

Для стандартной оценки Z из X это дает: ^[8]

${\displaystyle P\left({\frac {L-\mu }{\sigma }}<Z<{\frac {U-\mu }{\sigma }}\right)=\gamma .}$

Определив квантиль z такой, что

${\displaystyle P\left(-z<Z<z\right)=\gamma }$

следует:

${\displaystyle L=\mu -z\sigma ,\ U=\mu +z\sigma }$

Контроль над процессом

В приложениях управления процессами значение Z дает оценку степени отклонения процесса от запланированного.

Сравнение баллов, полученных по разным шкалам: ACT и SAT.

Показатель z для Студента А составил 1, что означает, что Студент А был на 1 стандартное отклонение выше среднего. Таким образом, студент А показал результаты SAT на уровне 84,13.

Когда баллы измеряются по разным шкалам, их можно преобразовать в z-показатели, чтобы облегчить сравнение. Дитц и др. ^[9] приводят следующий пример, сравнивая результаты учащихся по (старым) школьным тестам SAT и ACT . В таблице показано среднее и стандартное отклонение общего количества баллов по SAT и ACT. Предположим, что студент А набрал 1800 баллов по SAT, а студент Б — 24 балла по ACT. Какой студент показал лучшие результаты по сравнению с другими участниками теста?

Показатель z для студента Б составил 0,6, что означает, что стандартное отклонение студента Б было на 0,6 выше среднего. Таким образом, студент Б показал результаты SAT на уровне 72,57.

Z-показатель для студента А равен ${\displaystyle z={x-\mu \over \sigma }={1800-1500 \over 300}=1}$

Z-показатель для студента Б равен ${\displaystyle z={x-\mu \over \sigma }={24-21 \over 5}=0.6}$

Поскольку у студента А более высокий z-показатель, чем у студента Б, студент А показал лучшие результаты по сравнению с другими участниками теста, чем студент Б.

Процент наблюдений ниже z-показателя

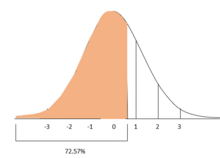
Продолжая пример с баллами ACT и SAT, если можно предположить, что баллы как ACT, так и SAT нормально распределены (что приблизительно верно), тогда z-показатели можно использовать для расчета процента тестируемых, получивших более низкую оценку. баллы, чем у студентов А и Б.

Кластерный анализ и многомерное масштабирование

«Для некоторых многомерных методов, таких как многомерное масштабирование и кластерный анализ, концепция расстояния между единицами данных часто представляет значительный интерес и важность… Когда переменные в многомерном наборе данных находятся в разных масштабах, имеет больше смысла рассчитывать расстояния после некоторой формы стандартизации». ^[10]

Анализ основных компонентов

При анализе главных компонентов «переменные, измеренные в разных масштабах или в общей шкале с сильно различающимися диапазонами, часто стандартизируются». ^[11]

Относительная важность переменных в множественной регрессии: стандартизированные коэффициенты регрессии

Стандартизация переменных перед множественным регрессионным анализом иногда используется в качестве вспомогательного средства для интерпретации. ^[12] (стр. 95) утверждают следующее.

«Наклон стандартизированной регрессии — это наклон уравнения регрессии, если X и Y стандартизированы… Стандартизация X и Y осуществляется путем вычитания соответствующих средних значений из каждого набора наблюдений и деления на соответствующие стандартные отклонения… В множественной регрессии, когда несколько Используются переменные X, стандартизированные коэффициенты регрессии количественно определяют относительный вклад каждой переменной X».

Однако Катнер и др. ^[13] (стр. 278) делают следующее предостережение: «…нужно с осторожностью интерпретировать любые коэффициенты регрессии, стандартизированные или нет. Причина в том, что, когда переменные-предикторы коррелируют между собой,… на коэффициенты регрессии влияют другие переменные-предикторы в модели... На величины стандартизированных коэффициентов регрессии влияет не только наличие корреляций между переменными-предикторами, но и интервалы наблюдений по каждой из этих переменных. Иногда эти интервалы могут быть совершенно произвольными. Следовательно, , обычно неразумно интерпретировать величины стандартизированных коэффициентов регрессии как отражающие сравнительную важность переменных-предикторов».

Стандартизация в математической статистике

В математической статистике случайная величина X стандартизируется путем вычитания ее ожидаемого значения и деления разницы на ее стандартное отклонение . ${\displaystyle \operatorname {E} [X]}$ ${\displaystyle \sigma (X)={\sqrt {\operatorname {Var} (X)}}:}$

${\displaystyle Z={X-\operatorname {E} [X] \over \sigma (X)}}$

Если рассматриваемая случайная величина является выборочным средним случайной выборки X : ${\displaystyle \ X_{1},\dots ,X_{n}}$

${\displaystyle {\bar {X}}={1 \over n}\sum _{i=1}^{n}X_{i}}$

тогда стандартизированная версия

${\displaystyle Z={\frac {{\bar {X}}-\operatorname {E} [{\bar {X}}]}{\sigma (X)/{\sqrt {n}}}}}$

При этом дисперсия стандартизированного выборочного среднего рассчитывалась следующим образом:

${\displaystyle {\begin{array}{l}\operatorname {Var} \left(\sum x_{i}\right)=\sum \operatorname {Var} (x_{i})=n\operatorname {Var} (x_{i})=n\sigma ^{2}\\\operatorname {Var} ({\overline {X}})=\operatorname {Var} \left({\frac {\sum x_{i}}{n}}\right)={\frac {1}{n^{2}}}\operatorname {Var} \left(\sum x_{i}\right)={\frac {n\sigma ^{2}}{n^{2}}}={\frac {\sigma ^{2}}{n}}\end{array}}}$

Т-оценка

В оценке образования T-показатель представляет собой стандартный балл Z, сдвинутый и масштабированный так, чтобы его среднее значение составляло 50, а стандартное отклонение - 10. ^{[14] [15] [16]} На японском языке он также известен как хенсати , где эта концепция гораздо более широко известен и используется при поступлении в среднюю школу и университет.

При измерении плотности костей Т-показатель представляет собой стандартный балл измерения по сравнению с популяцией здоровых 30-летних взрослых и имеет обычное среднее значение 0 и стандартное отклонение 1. ^[17]

Смотрите также

• Нормализация (статистика)
• соотношение омега
• Стандартное нормальное отклонение
• Расстояние Махаланобис
• Функция ошибки
• Стьюдентизированный остаток

Рекомендации

1. Малдерс, Мартин; Зандериги, Джулия, ред. (2017). Европейская школа физики высоких энергий 2015: Банско, Болгария, 2–15 сентября 2015 г. Желтые отчеты ЦЕРН: Материалы школы. Женева: ЦЕРН. ISBN 978-92-9083-472-4.
2. Гросс, Эйлам (06 ноября 2017 г.). «Практическая статистика по физике высоких энергий». Желтые отчеты ЦЕРН: Школьные материалы . 4/2017: 165–186. doi : 10.23730/CYRSP-2017-004.165.
3. Э. Крейциг (1979). Высшая инженерная математика (Четвертое изд.). Уайли. п. 880, экв. 5. ISBN 0-471-02140-7.
4. Шпигель, Мюррей Р.; Стивенс, Ларри Дж. (2008), Статистика очертаний Шаума (Четвертое изд.), McGraw Hill, ISBN 978-0-07-148584-5
5. Менденхолл, Уильям; Синчич, Терри (2007), Статистика техники и наук (Пятое изд.), Пирсон / Прентис Холл, ISBN 978-0131877061
6. Гланц, Стэнтон А.; Слинкер, Брайан К.; Нейландс, Торстен Б. (2016), Учебник по прикладной регрессии и дисперсионному анализу (Третье изд.), McGraw Hill, ISBN 978-0071824118
7. Ахо, Кен А. (2014), Фундаментальная и прикладная статистика для биологов (первое издание), Chapman & Hall / CRC Press, ISBN 978-1439873380
8. Э. Крейциг (1979). Высшая инженерная математика (Четвертое изд.). Уайли. п. 880, экв. 6. ISBN 0-471-02140-7.
9. Диц, Дэвид; Барр, Кристофер; Четинкая-Рундель, Моя (2012), Статистика OpenIntro (второе изд.), openintro.org
10. Эверитт, Брайан; Хотхорн, Торстен Дж. (2011), Введение в прикладной многомерный анализ с помощью R , Springer, ISBN 978-1441996497
11. Джонсон, Ричард; Wichern, Wichern (2007), Прикладной многомерный статистический анализ , Пирсон / Прентис Холл
12. Афифи, Абдельмонем; Мэй, Сюзанна К.; Кларк, Вирджиния А. (2012), Практический многомерный анализ (пятое изд.), Chapman & Hall/CRC, ISBN 978-1439816806
13. Катнер, Майкл; Нахтсхайм, Кристофер; Нетер, Джон (204), Прикладные модели линейной регрессии (Четвертое изд.), McGraw Hill, ISBN 978-0073014661
14. Джон Сальвия; Джеймс Исселдайк; Сара Уитмер (29 января 2009 г.). Оценка: в специальном и инклюзивном образовании. Cengage Обучение. стр. 43–. ISBN 978-0-547-13437-6.
15. Эдвард С. Нойкруг; Р. Чарльз Фосетт (1 января 2014 г.). Основы тестирования и оценки: практическое руководство для консультантов, социальных работников и психологов. Cengage Обучение. стр. 133–. ISBN 978-1-305-16183-2.
16. Рэнди В. Кампхаус (16 августа 2005 г.). Клиническая оценка интеллекта детей и подростков. Спрингер. стр. 123–. ISBN 978-0-387-26299-4.
17. «Измерение костной массы: что означают цифры» . Национальный ресурсный центр NIH по остеопорозу и связанным с ним заболеваниям костей . Национальный институт здоровья . Проверено 5 августа 2017 г.

дальнейшее чтение

• Кэрролл, Сьюзен Ровецци; Кэрролл, Дэвид Дж. (2002). Статистика стала простой для руководителей школ (иллюстрированное издание). Роуман и Литтлфилд. ISBN 978-0-8108-4322-6. Проверено 7 июня 2009 г.
• Ларсен, Ричард Дж.; Маркс, Моррис Л. (2000). Введение в математическую статистику и ее приложения (Третье изд.). п. 282. ИСБН 0-13-922303-7.

Внешние ссылки

• калькулятор z-оценки