
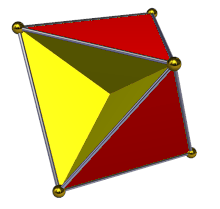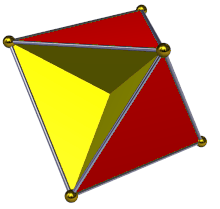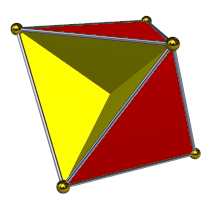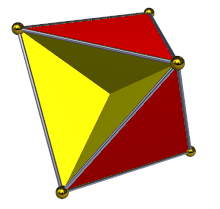
В геометрии тетрагемигексаэдр или полукубооктаэдр представляет собой однородный звездчатый многогранник , обозначаемый как U 4 . У него 7 граней (4 треугольника и 3 квадрата ), 12 ребер и 6 вершин. [1] Его вершина представляет собой перекрещенный четырехугольник . Его диаграмма Кокстера – Дынкина :![]()
![]()
![]()
![]()
![]()
![]()
![]() (хотя это двойное накрытие тетрагемишестиэдра).
(хотя это двойное накрытие тетрагемишестиэдра).
Тетрагемишестигранник — единственный непризматический однородный многогранник с нечетным числом граней. Его символ Витгофа — 3/2 3 | 2 , но представляет собой двойное покрытие тетраполушестигексаэдра восемью треугольниками и шестью квадратами, спаренными и совпадающими в пространстве. (Более интуитивно его можно рассматривать как два совпадающих тетрагемигексаэдра.)
Тетрагемишестиэдр является полуполиэдром . Часть имени «полугрань» означает, что некоторые грани образуют группу с вдвое меньшим количеством членов, чем у некоторого правильного многогранника — здесь три квадратных грани образуют группу с вдвое меньшим количеством граней, чем у правильного шестигранника, более известного как куб — отсюда полушестигранник . Грани полуграней также ориентированы в том же направлении, что и грани правильного многогранника. Три квадратных грани тетрагемишестиэдра, как и три грани куба, взаимно перпендикулярны .
Характеристика «вполовину меньше» также означает, что полуграни должны проходить через центр многогранника, где все они пересекаются друг с другом. Визуально каждый квадрат разделен на четыре прямоугольных треугольника , по два с каждой стороны.
Тетрагемигексаэдр — неориентируемая поверхность. Он уникален, поскольку является единственным однородным многогранником с эйлеровой характеристикой 1 и, следовательно, является проективным многогранником , что дает представление реальной проективной плоскости [2], очень похожее на римскую поверхность .
Тетрагемишестиэдр имеет те же вершины и ребра, что и правильный октаэдр . Он также разделяет 4 из 8 треугольных граней октаэдра, но имеет три дополнительных квадратных грани, проходящих через центр многогранника.
Двойственная фигура тетрагемишестиэдра — тетрагемигексакрон .
Тетраполушестигексаэдр 2-покрыт кубооктаэдром , [2] который соответственно имеет такую же абстрактную вершинную фигуру (2 треугольника и два квадрата: 3.4.3.4) и вдвое больше вершин, ребер и граней . Он имеет ту же топологию, что и абстрактный многогранник полукубооктаэдр .
Тетрагемигексаэдр также может быть построен в виде скрещенного треугольного куплоида . Все куплоиды и их двойники являются топологически проективными плоскостями. [3]
Тетрагемигексакрон — двойник тетрагемигексаэдра и один из девяти двойственных полуполиэдров .
Поскольку полумногогранники имеют грани, проходящие через центр, двойственные фигуры имеют соответствующие вершины в бесконечности; собственно, на реальной проективной плоскости на бесконечности. [4] В « Двойных моделях» Магнуса Веннингера они представлены в виде пересекающихся призм , каждая из которых простирается в обоих направлениях до одной и той же вершины на бесконечности, чтобы сохранить симметрию. На практике призмы модели обрезаются в определенном месте, удобном для производителя. Веннингер предположил, что эти фигуры являются членами нового класса звездчатых фигур, называемых звездчатыми до бесконечности . Однако он также предположил, что, строго говоря, они не являются многогранниками, поскольку их конструкция не соответствует обычным определениям.
Топологически считается, что тетрагемигексакрон содержит семь вершин. Три вершины, рассматриваемые на бесконечности ( действительная проективная плоскость на бесконечности), соответствуют по направлению трем вершинам полуоктаэдра , абстрактного многогранника. Остальные четыре вершины находятся в чередующихся углах центрального куба (полукуба , в данном случае тетраэдра ).