Призма (геометрия)

Твердое тело с двумя параллельными n-угольными основаниями, соединенными n параллелограммами.

В геометрии призма — это многогранник , состоящий из n -стороннего многоугольника в основании , второго основания, представляющего собой транслированную копию (жестко перемещаемую без вращения) первой, и n других граней , обязательно все параллелограммы , соединяющие соответствующие стороны двух оснований. . Все сечения, параллельные основаниям, являются трансляциями оснований. Призмы называются по основаниям, например, призма с пятиугольным основанием называется пятиугольной призмой. Призмы — подкласс призматоидов . ^[2]

Как и многие основные геометрические термины, слово « призма» (от греческого πρίσμα (призма)  «что-то распиленное») впервые было использовано в « Началах» Евклида . Евклид определил этот термин в книге XI как «твёрдую фигуру, состоящую из двух противоположных, равных и параллельных плоскостей, а остальные являются параллелограммами». Однако это определение подвергалось критике за недостаточную конкретность в отношении природы оснований (что вызывает некоторую путаницу среди поколений более поздних авторов геометрии). ^{[3] [4]}

Косой против правого

Косая призма — это призма, у которой соединяемые ребра и грани не перпендикулярны основным граням.

Пример: параллелепипед — это наклонная призма, основанием которой является параллелограмм или, что то же самое, многогранник с шестью гранями параллелограмма.

Правая призма

Правильная призма — это призма, у которой соединяемые ребра и грани перпендикулярны основным граням. ^[5] Это применимо тогда и только тогда, когда все соединяемые грани прямоугольные .

Двойственной прямой n - призме является правая n - бипирамида .

Правая призма (с прямоугольными сторонами) с правильными n -угольными основаниями имеет символ Шлефли { }×{ n }. Он приближается к цилиндру , когда n приближается к бесконечности . ^[6]

Особые случаи

• Прямую прямоугольную призму (с прямоугольным основанием) еще называют кубоидом или неофициально прямоугольным ящиком . Прямоугольная призма имеет символ Шлефли { }×{ }×{ }.
• Прямоугольную призму (с квадратным основанием) также называют квадратным кубоидом или неофициально квадратной коробкой .

Примечание. В некоторых текстах термин «прямоугольная призма» или «квадратная призма» может применяться как к прямой призме с прямоугольным основанием, так и к призме с прямым квадратным основанием.

Правильная призма

Правильная призма – это призма с правильными основаниями.

Равномерная призма

Однородная призма или полуправильная призма — это прямая призма с правильными основаниями и всеми ребрами одинаковой длины.

Таким образом, все боковые грани однородной призмы являются квадратами .

Таким образом, все грани однородной призмы являются правильными многоугольниками. Кроме того, такие призмы изогональны ; таким образом, они являются однородными многогранниками . Они образуют одну из двух бесконечных серий полуправильных многогранников , другую серию образуют антипризмы .

Равномерная n -угольная призма имеет символ Шлефли t{2, n }.

Объем

Объем призмы — это произведение площади основания на высоту, т . е. расстояние между двумя гранями основания (в случае непрямой призмы обратите внимание, что это означает расстояние по перпендикуляру).

Таким образом, объем составляет:

${\displaystyle V=Bh,}$

где B — площадь основания, а h — высота.

Следовательно, объем призмы, основанием которой является n -сторонний правильный многоугольник со стороной s, равен:

$${\displaystyle V={\frac {n}{4}}hs^{2}\cot {\frac {\pi }{n}}.}$$

Площадь поверхности

Площадь поверхности прямой призмы равна:

${\displaystyle 2B+Ph,}$

где B — площадь основания, h — высота, P — периметр основания .

Следовательно, площадь поверхности прямой призмы, основанием которой является правильный n -сторонний многоугольник с длиной стороны s и высотой h , равна:

${\displaystyle A={\frac {n}{2}}s^{2}\cot {\frac {\pi }{n}}+nsh.}$

Диаграммы Шлегеля

Симметрия

Группа симметрии правосторонней n -сторонней призмы с правильным основанием равна D n _{h порядка} 4 n , за исключением куба, который имеет большую группу симметрии Oh порядка 48, которая имеет три версии D _4h как подгруппы . Группа вращения — это D _n порядка 2 n , за исключением куба, который имеет большую группу симметрии O порядка 24, которая имеет три версии D ₄ в качестве подгрупп.

Группа симметрии D _{n h} содержит инверсию тогда и только тогда, когда n четно .

Осоэдры и диэдры также обладают двугранной симметрией, и n -угольная призма может быть построена путем геометрического усечения n - угольного осоэдра, а также путем сгибания или расширения n - угольного диэдра.

Усеченная призма

Пример усеченной треугольной призмы. Его верхняя грань усечена под косым углом, но это не косая призма.

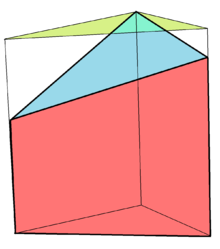
Усеченная призма образуется , когда призму разрезают плоскостью, не параллельной ее основаниям. У усеченной призмы основания не равны , а ее стороны не являются параллелограммами. ^[7]

Витая призма

Скрученная призма — это невыпуклый многогранник, построенный из однородной n -призмы, каждая боковая грань которой разделена пополам по диагонали квадрата, путем скручивания вершины, обычно наπ/нрадианы (180/нградусов) в одном и том же направлении, в результате чего стороны становятся вогнутыми. ^{[8] [9]}

Скрученную призму невозможно разрезать на тетраэдры без добавления новых вершин. Наименьший случай: треугольная форма, называется многогранником Шенхардта .

n - угольная скрученная призма топологически идентична n -угольной однородной антипризме , но имеет половину группы симметрии : D _n , [ n ,2] ⁺ , порядка 2 n . Его можно рассматривать как невыпуклую антипризму с удаленными тетраэдрами между парами треугольников.

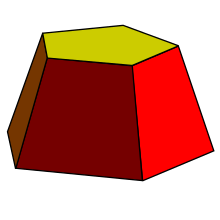
Усеченный конус

Усеченная пирамида — это конструкция, похожая на призму, с трапециевидными боковыми гранями и верхними и нижними многоугольниками разного размера.

Пример пятиугольной усеченной пирамиды

Звездная призма

Звездная призма — это невыпуклый многогранник, построенный из двух одинаковых граней звездчатого многоугольника сверху и снизу, параллельных, смещенных на расстояние и соединенных прямоугольными гранями. Однородная звездная призма будет иметь символ Шлефли { p / q } × { }, с p прямоугольниками и 2 гранями { p / q } . Топологически она идентична p -угольной призме.

Перекрещенная призма

Скрещенная призма — невыпуклый многогранник, построенный из призмы, вершины одного основания которой перевернуты вокруг центра этого основания (или повернуты на 180°). Это преобразует боковые прямоугольные грани в скрещенные прямоугольники . Основание правильного многоугольника имеет вид n -угольных песочных часов . Все косые ребра проходят через один центр тела. Примечание: в центре тела нет вершин. Скрещенная призма топологически идентична n -угольной призме.

Тороидальная призма

Тороидальная призма — это невыпуклый многогранник, подобный скрещенной призме , но без нижней и верхней граней основания, а также с простыми прямоугольными боковыми гранями, замыкающими многогранник. Это можно сделать только для односторонних базовых многоугольников. Это топологические торы с нулевой эйлеровой характеристикой . Топологическую многогранную сеть можно вырезать из двух рядов квадратной мозаики (с конфигурацией вершин 4.4.4.4 ): полосы из n квадратов, каждый из которых прикреплен к скрещенному прямоугольнику . n -угольная тороидальная призма имеет 2 n вершин, 2 n граней: n квадратов и n скрещенных прямоугольников, а также 4 n ребер. Оно топологически самодвойственно .

Призматический многогранник

Призматический многогранник — это многомерное обобщение призмы. n -мерный призматический многогранник состоит из двух ( n - 1 )-мерных многогранников, переведенных в следующее измерение.

Призматические элементы n -многогранника удваиваются из элементов ( n - 1 )-многогранника, а затем создаются новые элементы из следующего нижнего элемента.

Возьмем n -многогранник с элементами F _i i -грани ( i = 0, ..., n ). Его ( n + 1 )-многогранная призма будет иметь 2 F _i + F _{i −1} i -гранных элемента. (При F ₋₁ = 0 , F _n = 1. )

По размеру:

• Возьмем многоугольник с n вершинами и n ребрами. Его призма имеет 2 n вершин, 3 n ребер и 2 + n граней.
• Возьмем многогранник с вершинами V , ребрами E и гранями F. Его призма имеет 2 вершины V , 2 ребра E + V , 2 грани F + E и 2 + F ячеек.
• Возьмем полихорон с V вершинами, E ребрами, F гранями и C ячейками. Его призма имеет 2 вершины V , 2 ребра E + V , 2 грани F + E , 2 ячейки C + F и 2 + C гиперячейки.

Однородный призматический многогранник

Правильный n -многогранник, представленный символом Шлефли { p , q ,..., t }, может образовывать равномерный призматический ( n + 1 )-многогранник, представленный декартовым произведением двух символов Шлефли : { p , q ,... , т }×{ }.

По размеру:

• 0-многогранная призма — это отрезок прямой , представленный пустым символом Шлефли { }.

  

• 1-многогранная призма — это прямоугольник , составленный из двух сдвинутых отрезков прямой. Он представлен как произведение символа Шлефли { }×{ }. Если это квадрат , симметрию можно уменьшить: { }×{ } = {4}.

  Пример:, Квадрат, { }×{ }, два параллельных отрезка, соединенных двумя сторонами отрезка .

• Многоугольная призма — это трехмерная призма, состоящая из двух сдвинутых многоугольников, соединенных прямоугольниками . Правильный многоугольник { p } может составить равномерную n -угольную призму, представленную произведением { p }×{ }. Если p = 4 , с симметрией квадратных сторон он становится кубом : {4}×{ } = {4,3}.

  Пример:, Пятиугольная призма , {5}×{ }, два параллельных пятиугольника , соединенных 5 прямоугольными сторонами .

• Многогранная призма — это четырехмерная призма, состоящая из двух сдвинутых многогранников, соединенных трехмерными призматическими ячейками. Правильный многогранник { p , q } может построить равномерную полихорическую призму, представленную произведением { p , q }×{ }. Если многогранник и стороны являются кубами, он становится тессерактом : { 4,3}×{ } = {4,3,3}.

  Пример:, Додекаэдрическая призма , {5,3}×{ }, два параллельных додекаэдра , соединенных 12 сторонами пятиугольной призмы .

• ...

Дуопризма {23}×{29} , края которой видны в стереографической проекции . Квадраты образуют плоский тор с сеткой 23×29 .

Призматические многогранники более высокого порядка также существуют как декартово произведение любых двух или более многогранников. Размерность многогранника-произведения равна сумме размерностей его элементов. Первые их примеры существуют в 4-мерном пространстве; они называются дуопризмами как произведение двух многоугольников в 4-х измерениях.

Правильные дуопризмы представлены как { p }×{ q }, с pq вершинами, 2 pq ребрами, pq квадратными гранями, p q -угольными гранями, q p -угольными гранями и ограничены p q -угольными призмами и q p -угольными гранями . призмы.

Например, {4}×{4}, дуопризма 4–4 , является формой более низкой симметрии тессеракта , как и {4,3}×{ }, кубическая призма . {4}×{4}×{ } (призма дуопризмы 4-4), {4,3}×{4} (дуопризма куба-4) и {4,3,3}×{ } (тессерактическая призма) расположены ниже формы симметрии 5-куба .

Смотрите также

• Апейрогональная призма
• Выпрямленная призма
• Призманес
• Список фигур

Рекомендации

1. Джонсон, Северо-Запад (2018). «Глава 11: Конечные группы симметрии». Геометрии и преобразования. ISBN 978-1-107-10340-5.См. 11.3 Пирамиды, призмы и антипризмы, рисунок 11.3b.
2. Грюнбаум, Бранко (1997). «Изогональные призматоиды». Дискретная и вычислительная геометрия . 18 :13–52. дои : 10.1007/PL00009307 .
3. Мальтон, Томас (1774). Королевская дорога к геометрии: или простое и знакомое введение в математику. автор, и продал. п. 360.
4. Эллиот, Джеймс (1845). Ключ к полному трактату по практической геометрии и измерениям: содержащий полную демонстрацию правил. Лонгман, Браун, Грин и Лонгманс. п. 3.
5. Керн, Уильям Ф.; Бланд, Джеймс Р. (1938). Твердые измерения с доказательствами . п. 28.
6. Геретшлагер, Роберт (2020). Привлечение молодежи к занятиям математикой через олимпиады: мировые перспективы и практика. Том. 1. Всемирный научный . п. 39. ИСБН 978-981-120-582-8.
7. Керн и Бланд (1938), стр. 81.
8. Горини, Кэтрин А. (2003). Факты в деле: Справочник по геометрии. п. 172. ИСБН 0-8160-4875-4.
9. «Изображения искривленных призм».

• Энтони Пью (1976). Многогранники: визуальный подход . Калифорния: Издательство Калифорнийского университета в Беркли. ISBN 0-520-03056-7.Глава 2: Архимедовы многогранники, призмы и антипризмы

Внешние ссылки

• Вайсштейн, Эрик В. «Призма». Математический мир .
• Бумажные модели призм и антипризм Бесплатные сетки призм и антипризм
• Бумажные модели призм и антипризм с использованием сеток, созданных Стеллой.