stringtranslate.com

Черное тело

Физическое приближение модели излучателя черного тела состоит из нагреваемой пирографитовой камеры и периферийных устройств, обеспечивающих стабильность температуры.
Излучатель черного тела, используемый в лаборатории CARLO в Польше. Это приближение модели, описываемой законом Планка , используемой в качестве стандарта спектральной освещенности .

По мере снижения температуры черного тела интенсивность его излучения также уменьшается, а его пик смещается в сторону более длинных волн. Для сравнения показан классический закон Рэлея-Джинса и его ультрафиолетовая катастрофа .

Черное тело или черное тело — это идеализированное физическое тело , которое поглощает все падающее электромагнитное излучение , независимо от частоты или угла падения . Излучение, испускаемое черным телом в тепловом равновесии с окружающей средой, называется излучением черного тела . Название «черное тело» дано потому, что оно поглощает все цвета света. Напротив, белое тело — это тело с «шероховатой поверхностью, которая отражает все падающие лучи полностью и равномерно во всех направлениях». [1]

Черное тело в тепловом равновесии (то есть при постоянной температуре) испускает электромагнитное излучение черного тела. Излучение испускается в соответствии с законом Планка , что означает, что его спектр определяется только температурой (см. рисунок справа), а не формой или составом тела.

Идеальное черное тело в тепловом равновесии имеет два основных свойства: [2]

  1. Это идеальный излучатель: на каждой частоте он излучает столько же или больше тепловой лучистой энергии, чем любое другое тело при той же температуре.
  2. Это диффузный излучатель: энергия, измеренная на единицу площади, перпендикулярной направлению, излучается изотропно , независимо от направления.

Реальные материалы излучают энергию на уровне доли — называемой излучательной способностью — уровней энергии черного тела. По определению, черное тело в тепловом равновесии имеет излучательную способность ε = 1. Источник с более низкой излучательной способностью, независимо от частоты, часто называют серым телом. [3] [4] Создание черных тел с излучательной способностью, максимально близкой к 1, остается актуальной темой. [5]

В астрономии излучение звезд и планет иногда характеризуется эффективной температурой — температурой черного тела, которое излучало бы такой же полный поток электромагнитной энергии.

Определение

Идея абсолютно черного тела была первоначально введена Густавом Кирхгофом в 1860 году следующим образом:

...предположение, что можно представить себе тела, которые при бесконечно малой толщине полностью поглощают все падающие лучи и не отражают и не пропускают ни одного. Я буду называть такие тела совершенно черными , или, короче, черными телами . [6]

Более современное определение исключает ссылку на «бесконечно малые толщины»: [7]

Теперь определено идеальное тело, называемое черным телом . Черное тело позволяет всему падающему излучению проходить в него (без отраженной энергии) и внутренне поглощает все падающее излучение (энергия не проходит через тело). Это справедливо для излучения всех длин волн и для всех углов падения. Следовательно, черное тело является идеальным поглотителем всего падающего излучения. [8]

Идеализации

В этом разделе описываются некоторые концепции, разработанные в связи с черными телами.

Приблизительная реализация черного тела в виде крошечного отверстия в изолированном корпусе.

Полость с отверстием

Широко используемая модель черной поверхности — это небольшое отверстие в полости со стенками, непрозрачными для излучения. [8] Излучение, падающее на отверстие, пройдет в полость и вряд ли будет переизлучено, если полость большая. Отсутствие переизлучения означает, что отверстие ведет себя как идеально черная поверхность. Отверстие не совсем идеально черная поверхность — в частности, если длина волны падающего излучения больше диаметра отверстия, часть будет отражаться. Аналогично, даже в идеальном тепловом равновесии излучение внутри полости конечного размера не будет иметь идеальный планковский спектр для длин волн, сопоставимых или больших, чем размер полости. [9]

Предположим, что полость поддерживается при фиксированной температуре T , а излучение, запертое внутри оболочки, находится в тепловом равновесии с оболочкой. Отверстие в оболочке позволит некоторой части излучения выходить. Если отверстие небольшое, излучение, входящее и выходящее из отверстия, оказывает незначительное влияние на равновесие излучения внутри полости. Это выходящее излучение будет приближаться к излучению черного тела , которое демонстрирует распределение энергии, характерное для температуры T , и не зависит от свойств полости или отверстия, по крайней мере для длин волн, меньших размера отверстия. [9] См. рисунок во Введении для спектра как функции частоты излучения , которая связана с энергией излучения уравнением E = hf , где E = энергия, h = постоянная Планка , f = частота.

В любой момент времени излучение в полости может не находиться в тепловом равновесии, но второй закон термодинамики гласит, что если его не трогать, оно в конечном итоге достигнет равновесия, [10] хотя время, необходимое для этого, может быть очень большим. [11] Обычно равновесие достигается путем постоянного поглощения и испускания излучения материалом в полости или ее стенками. [12] [13] [14] [15] Излучение, попадающее в полость, будет « термализоваться » этим механизмом: энергия будет перераспределяться до тех пор, пока ансамбль фотонов не достигнет распределения Планка . Время, необходимое для термализации, намного меньше в присутствии конденсированного вещества, чем в разреженном веществе, таком как разреженный газ. При температурах ниже миллиардов Кельвинов прямые взаимодействия фотонов [16] обычно незначительны по сравнению с взаимодействиями с веществом. [17] Фотоны являются примером взаимодействующего бозонного газа, [18] и, как описано в H-теореме , [19] при очень общих условиях любой взаимодействующий бозонный газ будет приближаться к тепловому равновесию.

Передача, поглощение и отражение

Поведение тела по отношению к тепловому излучению характеризуется его пропусканием τ , поглощением α и отражением ρ .

Граница тела образует интерфейс с его окружением, и этот интерфейс может быть шероховатым или гладким. Неотражающий интерфейс, разделяющий области с разными показателями преломления, должен быть шероховатым, поскольку законы отражения и преломления, управляемые уравнениями Френеля для гладкого интерфейса, требуют отраженного луча, когда показатели преломления материала и его окружения различаются. [20] Нескольким идеализированным типам поведения даны особые названия:

Непрозрачное тело — это тело, которое не пропускает ни одного из достигающих его излучений, хотя часть его может отражаться. [21] [22] То есть τ = 0 и α + ρ = 1.

Прозрачное тело — это тело, которое пропускает все достигающее его излучение. То есть τ = 1 и α = ρ = 0.

Серым телом называется тело, у которого α , ρ и τ постоянны для всех длин волн; этот термин также используется для обозначения тела, у которого α не зависит от температуры и длины волны.

Белое тело — это тело, для которого все падающее излучение отражается равномерно во всех направлениях: τ = 0, α = 0 и ρ = 1.

Для черного тела τ = 0, α = 1 и ρ = 0. Планк предлагает теоретическую модель для абсолютно черных тел, которые, как он отметил, не существуют в природе: помимо их непрозрачной внутренней части, они имеют интерфейсы, которые идеально пропускают и не отражают свет. [23]

Идеально черные тела Кирхгофа

Кирхгоф в 1860 году ввел теоретическую концепцию абсолютно черного тела с полностью поглощающим поверхностным слоем бесконечно малой толщины, но Планк отметил некоторые серьезные ограничения этой идеи. Планк отметил три требования к абсолютно черному телу: тело должно (i) позволять излучению проникать внутрь, но не отражать его; (ii) обладать минимальной толщиной, достаточной для поглощения падающего излучения и предотвращения его повторного излучения; (iii) удовлетворять серьезным ограничениям по рассеянию , чтобы предотвратить проникновение излучения и его отражение обратно. Как следствие, абсолютно черные тела Кирхгофа, поглощающие все падающее на них излучение, не могут быть реализованы в бесконечно тонком поверхностном слое и налагают условия на рассеяние света внутри черного тела, которые трудно удовлетворить. [24] [25]

Реализации

Реализация черного тела относится к реальному миру, физическому воплощению. Вот несколько .

Полость с отверстием

В 1898 году Отто Луммер и Фердинанд Курльбаум опубликовали отчет о своем источнике излучения в виде полости. [26] Их конструкция используется в основном без изменений для измерений излучения по сей день. Это было отверстие в стенке платиновой коробки, разделенное диафрагмами, с его внутренней частью, зачерненной оксидом железа. Это был важный ингредиент для постепенно улучшающихся измерений, которые привели к открытию закона Планка. [27] [28] Версия, описанная в 1901 году, имела внутреннюю часть, зачерненную смесью оксидов хрома, никеля и кобальта. [29] См. также Hohlraum .

Почти черные материалы

Существует интерес к материалам, подобным черному телу, для камуфляжа и материалам, поглощающим радиолокационные сигналы, для невидимости радаров. [30] [31] Они также применяются в качестве коллекторов солнечной энергии и инфракрасных тепловых детекторов. Как идеальный излучатель излучения, горячий материал с поведением черного тела создал бы эффективный инфракрасный нагреватель, особенно в космосе или в вакууме, где конвективный нагрев недоступен. [32] Они также полезны в телескопах и камерах в качестве антибликовых поверхностей для уменьшения рассеянного света и для сбора информации об объектах в высококонтрастных областях (например, наблюдение за планетами на орбите вокруг своих звезд), где материалы, подобные черному телу, поглощают свет, который исходит от неправильных источников.

Давно известно, что покрытие из ламповой сажи делает тело почти черным. Улучшение ламповой сажи обнаружено в изготовленных углеродных нанотрубках . Нанопористые материалы могут достигать показателей преломления, близких к показателям вакуума, в одном случае достигая среднего коэффициента отражения 0,045%. [5] [33] В 2009 году группа японских ученых создала материал под названием nanoblack, который близок к идеальному черному телу, на основе вертикально выровненных однослойных углеродных нанотрубок . Он поглощает от 98% до 99% входящего света в спектральном диапазоне от ультрафиолетового до дальнего инфракрасного диапазона. [32]

Другими примерами почти идеально черных материалов являются суперчерный , полученный путем химического травления сплава никеля и фосфора [34] , вертикально выровненные массивы углеродных нанотрубок (например, Vantablack ) и цветочные углеродные наноструктуры; [35] все они поглощают 99,9% света или более.

Звезды и планеты

Диаграмма, сравнивающая кривые реакции рецепторов красного, зеленого и синего света в глазах человека с приблизительными кривыми черного тела ряда звезд: Антарес ( красный сверхгигант ), Солнце ( желтый карлик ), Сириус ( белая звезда главной последовательности ), Спика (голубая звезда) и Гамма Парусов .

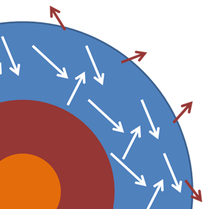
Звезда или планета часто моделируется как черное тело, а электромагнитное излучение, испускаемое этими телами, как излучение черного тела . На рисунке показано очень схематичное поперечное сечение для иллюстрации идеи. Фотосфера звезды, где генерируется испускаемый свет, идеализируется как слой, внутри которого фотоны света взаимодействуют с материалом в фотосфере и достигают общей температуры T , которая поддерживается в течение длительного периода времени. Некоторые фотоны вылетают и испускаются в космос, но энергия, которую они уносят, заменяется энергией изнутри звезды, так что температура фотосферы почти постоянна. Изменения в ядре приводят к изменениям в подаче энергии в фотосферу, но такие изменения медленны в рассматриваемом здесь временном масштабе. Если предположить, что эти обстоятельства могут быть реализованы, внешний слой звезды в некоторой степени аналогичен примеру оболочки с небольшим отверстием в нем, причем отверстие заменено ограниченным пропусканием в космос снаружи фотосферы. При всех этих предположениях звезда испускает излучение черного тела при температуре фотосферы. [36]

Идеализированный вид поперечного сечения звезды. Фотосфера содержит фотоны света, находящиеся почти в тепловом равновесии, и некоторые из них выходят в космос в виде излучения почти черного тела.

Используя эту модель, оценивается эффективная температура звезд, определяемая как температура черного тела, которое дает тот же поверхностный поток энергии, что и звезда. Если бы звезда была черным телом, та же эффективная температура была бы получена из любой области спектра. Например, сравнение в диапазоне B (синий) или V (видимый) приводит к так называемому индексу цвета BV , который увеличивается, чем краснее звезда, [37] при этом у Солнца индекс составляет +0,648 ± 0,006. [38] Объединение индексов U (ультрафиолетовый) и B приводит к индексу UB , который становится более отрицательным, чем горячее звезда и чем больше УФ-излучение. Предполагая, что Солнце является звездой типа G2 V, его индекс UB равен +0,12. [39] Два индекса для двух типов наиболее распространенных последовательностей звезд сравниваются на рисунке (диаграмма) с эффективной температурой поверхности звезд, если бы они были абсолютно черными телами. Существует грубая корреляция. Например, для данного измерения индекса BV кривые обеих наиболее распространенных последовательностей звезд (главной последовательности и сверхгигантов) лежат ниже соответствующего индекса UB черного тела , который включает ультрафиолетовый спектр, показывая, что обе группы звезд излучают меньше ультрафиолетового света, чем черное тело с тем же индексом BV . Возможно, удивительно, что они так хорошо соответствуют кривой черного тела, учитывая, что звезды имеют сильно различающиеся температуры на разных глубинах. [40] Например, Солнце имеет эффективную температуру 5780 К, [41] что можно сравнить с температурой его фотосферы (области, генерирующей свет), которая колеблется от примерно 5000 К на ее внешней границе с хромосферой до примерно 9500 К на ее внутренней границе с конвективной зоной глубиной примерно 500 км (310 миль). [42]

Эффективная температура черного тела в сравнении с показателями цвета BV и UB звезд главной последовательности и сверхгигантов на так называемой диаграмме цвет-цвет . [43]

Черные дыры

Черная дыра — это область пространства-времени, из которой ничто не ускользает. Вокруг черной дыры есть математически определенная поверхность, называемая горизонтом событий , которая отмечает точку невозврата . Она называется «черной», потому что поглощает весь свет, который попадает на горизонт, ничего не отражая, что делает ее почти идеальным черным телом [44] (излучение с длиной волны, равной или большей диаметра дыры, может не поглощаться, поэтому черные дыры не являются идеально черными телами). [45] Физики считают, что для внешнего наблюдателя черные дыры имеют ненулевую температуру и испускают излучение черного тела , излучение с почти идеальным спектром черного тела, в конечном итоге испаряясь . [46] Механизм этого излучения связан с вакуумными флуктуациями , в которых виртуальная пара частиц разделяется гравитацией дыры, один член всасывается в дыру, а другой испускается. [47] Распределение энергии излучения описывается законом Планка с температурой T :

где c — скорость света , ℏ — приведенная постоянная Планка , k B — постоянная Больцмана , G — гравитационная постоянная , а M — масса черной дыры. [48] Эти предсказания еще не были проверены ни наблюдательно, ни экспериментально. [49]

Космическое микроволновое фоновое излучение

Теория Большого взрыва основана на космологическом принципе , который гласит, что в больших масштабах Вселенная однородна и изотропна. Согласно теории, Вселенная примерно через секунду после своего образования была почти идеальным черным телом в тепловом равновесии при температуре выше 10 10 К. Температура уменьшалась по мере расширения Вселенной, а материя и излучение в ней охлаждались. Наблюдаемое сегодня космическое микроволновое фоновое излучение является «самым совершенным черным телом, когда-либо измеренным в природе». [50] Оно имеет почти идеальный спектр Планка при температуре около 2,7 К. Оно отличается от идеальной изотропии истинного излучения черного тела наблюдаемой анизотропией, которая меняется с углом на небе только примерно на одну часть из 100 000.

Радиационное охлаждение

Логарифмические графики зависимости пиковой длины волны излучения и светимости от температуры черного тела – красные стрелки показывают, что черные тела с температурой 5780 К имеют пиковую длину волны 501 нм и светимость 63,3 МВт/ м2 ; светимость

Интеграция закона Планка по всем частотам дает полную энергию за единицу времени на единицу площади поверхности, излучаемую черным телом, поддерживаемым при температуре T , и известна как закон Стефана-Больцмана :

где σ — постоянная Стефана–Больцмана , σ  ≈ 5,67 × 10−8  Вт⋅м −2 ⋅К −4 ‍ [ 51 ] Чтобы оставаться в тепловом равновесии при постоянной температуре T , черное тело должно поглощать или внутренне генерировать это количество мощности P на заданной площади A.

Охлаждение тела за счет теплового излучения часто аппроксимируется с помощью закона Стефана–Больцмана, дополненного излучательной способностью «серого тела» ε ≤ 1 ( P / A = εσT 4 ). Скорость снижения температуры излучающего тела можно оценить по излучаемой мощности и теплоемкости тела . [52] Этот подход является упрощением, которое игнорирует детали механизмов, лежащих в основе перераспределения тепла (которые могут включать изменение состава, фазовые переходы или перестройку тела), которые происходят внутри тела при его охлаждении, и предполагает, что в каждый момент времени тело характеризуется одной температурой. Он также игнорирует другие возможные осложнения, такие как изменение излучательной способности с температурой, [53] [54] и роль других сопутствующих форм излучения энергии, например, излучение частиц, таких как нейтрино. [55]

Если предполагается, что горячее излучающее тело подчиняется закону Стефана-Больцмана, а его мощность излучения P и температура T известны, этот закон можно использовать для оценки размеров излучающего объекта, поскольку общая излучаемая мощность пропорциональна площади излучающей поверхности. Таким образом, было обнаружено, что рентгеновские всплески, наблюдаемые астрономами, возникли в нейтронных звездах с радиусом около 10 км, а не в черных дырах, как предполагалось изначально. [56] Точная оценка размера требует некоторых знаний об излучательной способности, в частности, ее спектральной и угловой зависимости. [57]

Смотрите также

Ссылки

Цитаты

  1. ↑ Планк 1914, стр. 9–10.
  2. ^ Махмуд Массуд (2005). "§2.1 Излучение черного тела". Инженерные терможидкости: термодинамика, механика жидкости и теплопередача . Springer. стр. 568. ISBN 978-3-540-22292-7.
  3. ^ Излучательная способность поверхности в принципе зависит от частоты, угла зрения и температуры. Однако, по определению, излучение серого тела просто пропорционально излучению черного тела при той же температуре, поэтому его излучательная способность не зависит от частоты (или, что эквивалентно, длины волны). См. Massoud Kaviany (2002). "Рисунок 4.3(b): Поведение серой (без зависимости от длины волны), диффузной (без направленной зависимости) и непрозрачной (без пропускания) поверхности". Принципы теплопередачи . Wiley-IEEE. стр. 381. ISBN 978-0-471-43463-4.и Рональд Г. Дриггерс (2003). Энциклопедия оптической инженерии, том 3. CRC Press. стр. 2303. ISBN 978-0-8247-4252-2.
  4. ^ Некоторые авторы описывают источники инфракрасного излучения с излучательной способностью более примерно 0,99 как черное тело. См. «Что такое черное тело и инфракрасное излучение?». Вкладка «Образование/Справочник» . Electro Optical Industries, Inc. 2008. Архивировано из оригинала 7 марта 2016 г. Получено 10 июня 2019 г.
  5. ^ ab Chun, Ai Lin (2008). "Чернее черного". Nature Nanotechnology . doi : 10.1038/nnano.2008.29 .
  6. ↑ Перевод Ф. Гатри из Annalen der Physik : 109 , 275-301 (1860): Г. Кирхгоф (июль 1860). «О соотношении между излучательной и поглощающей способностью различных тел для света и тепла». Лондонский, Эдинбургский и Дублинский философский журнал и научный журнал . 20 (130).
  7. ^ Понятие бесконечно тонкого слоя было отброшено Планком. См. Планк 1914, стр. 10, сноска 2.
  8. ^ ab Siegel, Robert; Howell, John R. (2002). Теплопередача посредством теплового излучения; Том 1 (4-е изд.). Taylor & Francis. стр. 7. ISBN 978-1-56032-839-1.
  9. ^ ab Поправки к спектру возникают в связи с граничными условиями на стенках, кривизной и топологией, особенно для длин волн, сопоставимых с размерами полости; см. Roger Dale Van Zee; J. Patrick Looney (2002). Cavity-enhanced spectroscopies. Academic Press. стр. 202. ISBN 978-0-12-475987-9.
  10. ^ Клемент Джон Адкинс (1983). "§4.1 Функция второго закона". Равновесная термодинамика (3-е изд.). Cambridge University Press. стр. 50. ISBN 978-0-521-27456-2.
  11. ^ В простых случаях приближение к равновесию регулируется временем релаксации . В других случаях система может «зависнуть» в метастабильном состоянии , как утверждает Адкинс (1983) на стр. 10. Другой пример см. Мишель Ле Беллак; Фабрис Мортессань; Гассан Джордж Батруни (2004). Равновесная и неравновесная статистическая термодинамика. Cambridge University Press. стр. 8. ISBN 978-0521821438.
  12. ^ Приближение к тепловому равновесию излучения в полости может быть катализировано добавлением небольшого кусочка вещества, способного излучать и поглощать на всех частотах. См. Питер Теодор Ландсберг (1990). Термодинамика и статистическая механика (Переиздание Oxford University Press 1978 ed.). Courier Dover Publications. стр. 209. ISBN 978-0-486-66493-4.
  13. ^ Планк 1914, стр. 44, §52
  14. ^ Лаудон 2000, Глава 1
  15. ^ Мандель и Вольф 1995, Глава 13
  16. ^ Роберт Карплус* и Морис Нойман, «Рассеяние света светом», Phys. Rev. 83, 776–784 (1951)
  17. ^ Людвиг Бергманн; Клеменс Шефер; Хайнц Нидриг (1999). Оптика волн и частиц. Вальтер де Грюйтер. п. 595. ИСБН 978-3-11-014318-8Поскольку взаимодействие фотонов друг с другом пренебрежимо мало, для установления термодинамического равновесия теплового излучения необходимо небольшое количество вещества.
  18. ^ Фундаментальные бозоны — это фотон , векторные бозоны слабого взаимодействия , глюон и гравитон . См. Аллан Гриффин; Д. В. Сноук ; С. Стрингари (1996). Бозе-Эйнштейновская конденсация. Cambridge University Press. стр. 4. ISBN 978-0-521-58990-1.
  19. ^ Ричард Чейс Толман (2010). "§103: Изменение H со временем в результате столкновений". Принципы статистической механики (Переиздание 1938 Oxford University Press ed.). Dover Publications. стр. 455 и далее . ISBN 978-0-486-63896-6... мы можем определить подходящую величину H для характеристики состояния газа, которое [будет проявлять] тенденцию к уменьшению со временем в результате столкновений, если только распределение молекул [уже не является] равновесным. (стр. 458)
  20. ^ Пол А. Типлер (1999). "Относительная интенсивность отраженного и прошедшего света". Физика для ученых и инженеров, части 1-35; часть 39 (4-е изд.). Macmillan. стр. 1044. ISBN 978-0-7167-3821-3.
  21. ^ Массуд Кавьяни (2002). "Рисунок 4.3(b) Свойства излучения непрозрачной поверхности". Принципы теплопередачи . Wiley-IEEE. стр. 381. ISBN 978-0-471-43463-4.
  22. ^ BA Venkanna (2010). "§10.3.4 Поглощающая способность, отражательная способность и пропускаемость". Основы тепло- и массопереноса . PHI Learning Pvt. Ltd. стр. 385–386. ISBN 978-81-203-4031-2.
  23. ^ Планк 1914, стр. 10
  24. ↑ Планк 1914, стр. 9–10, §10
  25. ^ Кирхгоф 1860c
  26. ^ Люммер и Курлбаум 1898
  27. ^ Обширное историческое обсуждение можно найти в Mehra, Jagdish ; Rechenberg, Helmut (2000). Историческое развитие квантовой теории. Springer. стр. 39 и далее . ISBN 978-0-387-95174-4.
  28. ^ Кангро 1976, стр. 159
  29. ^ Люммер и Курлбаум 1901
  30. ^ CF Lewis (июнь 1988). «Материалы сохраняют сдержанность» (PDF) . Mech. Eng. : 37–41.[ постоянная мертвая ссылка ]
  31. ^ Брэдли Куинн (2010). Текстильное будущее. Берг. стр. 68. ISBN 978-1-84520-807-3.
  32. ^ ab K. Mizuno; et al. (2009). "Поглотитель черного тела из вертикально выровненных однослойных углеродных нанотрубок". Труды Национальной академии наук . 106 (15): 6044–6077. Bibcode : 2009PNAS..106.6044M. doi : 10.1073/pnas.0900155106 . PMC 2669394. PMID  19339498 . 
  33. ^ Цзу-По Янг ​​и др. (2008). «Экспериментальное наблюдение чрезвычайно темного материала, созданного массивом нанотрубок низкой плотности». Nano Letters . 8 (2): 446–451. Bibcode : 2008NanoL...8..446Y. doi : 10.1021/nl072369t. PMID  18181658. S2CID  7412160.
  34. ^ См. описание работы Ричарда Брауна и его коллег из Национальной физической лаборатории Великобритании: Мик Хамер (6 февраля 2003 г.). «Мини-кратеры — ключ к „самому черному из когда-либо существовавших“». New Scientist .
  35. ^ Гай, Виней; Сингх, Харприт; Агнихотри, Прабхат К. (2019). «Углеродные нанотрубки, похожие на одуванчики, для почти идеальных черных поверхностей». ACS Applied Nano Materials . 2 (12): 7951–7956. doi :10.1021/acsanm.9b01950. S2CID  213017898.
  36. ^ Саймон Ф. Грин; Марк Х. Джонс; С. Джоселин Бернелл (2004). Введение в солнце и звезды. Cambridge University Press. С. 21–22, 53. ISBN 978-0-521-54622-5Источник, в котором фотоны с гораздо большей вероятностью будут взаимодействовать с материалом внутри источника, чем выходить из него, является условием для формирования спектра черного тела .
  37. ^ Дэвид Х. Келли; Юджин Ф. Милон; Энтони Ф. (FRW) Авени (2011). Исследование древних небес: обзор древней и культурной астрономии (2-е изд.). Springer. стр. 52. ISBN 978-1-4419-7623-9.
  38. ↑ Дэвид Ф. Грей (февраль 1995 г.). «Сравнение Солнца с другими звездами по температурной координате». Публикации Астрономического общества Тихого океана . 107 : 120–123. Bibcode : 1995PASP..107..120G. doi : 10.1086/133525 .
  39. ^ M Golay (1974). "Таблица IX: Индексы UB". Введение в астрономическую фотометрию . Springer. стр. 82. ISBN 978-90-277-0428-3.
  40. ^ Лоуренс Хью Аллер (1991). Атомы, звезды и туманности (3-е изд.). Cambridge University Press. стр. 61. ISBN 978-0-521-31040-6.
  41. ^ Кеннет Р. Лэнг (2006). Астрофизические формулы, Том 1 (3-е изд.). Биркхойзер. стр. 23. ISBN 978-3-540-29692-8.
  42. ^ Б. Бертотти; Паоло Фаринелла; Дэвид Вокроухлицкий (2003). "Рисунок 9.2: Температурный профиль в солнечной атмосфере". Новые виды Солнечной системы . Springer. стр. 248. ISBN 978-1-4020-1428-4.
  43. ^ Рисунок смоделирован по Э. Бём-Витенсе (1989). "Рисунок 4.9". Введение в звездную астрофизику: основные звездные наблюдения и данные . Cambridge University Press. стр. 26. ISBN 978-0-521-34869-0.
  44. ^ Шутц, Бернард (2004). Гравитация от Group Up: Вводное руководство по гравитации и общей теории относительности (1-е изд.). Cambridge University Press. стр. 304. ISBN 978-0-521-45506-0.
  45. ^ PCW Davies (1978). "Термодинамика черных дыр" (PDF) . Rep Prog Phys . 41 (8): 1313–1355. Bibcode :1978RPPh...41.1313D. doi :10.1088/0034-4885/41/8/004. S2CID  250916407. Архивировано из оригинала (PDF) 10 мая 2013 г.
  46. ^ Роберт М. Вальд (2005). «Термодинамика черных дыр». В Андрес Гомберофф; Дональд Марольф (ред.). Лекции по квантовой гравитации . Springer Science & Business Media . стр. 1–38. ISBN 978-0-387-23995-8.
  47. ^ Бернард Дж. Карр и Стивен Б. Гиддингс (2008). "Глава 6: Квантовые черные дыры". Beyond Extreme Physics: Передовая наука. Rosen Publishing Group, Scientific American (COR). стр. 30. ISBN 978-1-4042-1402-6.
  48. ^ Валерий П. Фролов; Андрей Зельников (2011). "Уравнение 9.7.1". Введение в физику черных дыр . Oxford University Press. стр. 321. ISBN 978-0-19-969229-3.
  49. ^ Роберт М. Вальд (2005). "Термодинамика черных дыр (стр. 1–38)". В Андрес Гомберофф; Дональд Марольф (ред.). Лекции по квантовой гравитации . Springer Science & Business Media . стр. 28. ISBN 978-0-387-23995-8... никакие результаты термодинамики черных дыр не подвергались экспериментальным или наблюдательным проверкам...
  50. ^ Уайт, М. (1999). "Анизотропия в реликтовом излучении" (PDF) . Труды конференции в Лос-Анджелесе, DPF 99. Калифорнийский университет в Лос-Анджелесе .См. также arXive.org.
  51. ^ "2022 CODATA Value: Stefan–Boltzmann constant". Справочник NIST по константам, единицам и неопределенности . NIST . Май 2024. Получено 18 мая 2024 .
  52. ^ Простой пример приводит Шривастава МК (2011). «Охлаждение излучением». Руководство по объективной физике для IIT-JEE . Pearson Education India. стр. 610. ISBN 978-81-317-5513-6.
  53. ^ M Vollmer; KP Mõllmann (2011). "Рисунок 1.38: Некоторые примеры температурной зависимости излучательной способности для различных материалов". Инфракрасное тепловидение: основы, исследования и применение . John Wiley & Sons. стр. 45. ISBN 978-3-527-63087-5.
  54. ^ Роберт Осиандер; М. Энн Гаррисон Даррин; Джон Чемпион (2006). MEMS и микроструктуры в аэрокосмических приложениях. CRC Press. стр. 187. ISBN 978-0-8247-2637-9.
  55. ^ Кришна Раджагопал; Фрэнк Вильчек (2001). "6.2 Окисление нейтринными излучениями (стр. 2135-2136) – Физика конденсированных сред КХД". В Михаил А. Шифман (ред.). На переднем крае физики элементарных частиц: Справочник по КХД (по случаю 75-летия профессора Бориса Иоффе) . Том 3. Сингапур: World Scientific . стр. 2061–2151. arXiv : hep-ph/0011333v2 . CiteSeerX 10.1.1.344.2269 . doi :10.1142/9789812810458_0043. ISBN  978-981-02-4969-4. S2CID  13606600. В течение первых 10 5–6 лет своей жизни охлаждение нейтронной звезды регулируется балансом между теплоемкостью и потерей тепла за счет испускания нейтрино. ... Как удельная теплоемкость C V , так и скорость испускания нейтрино L ν определяются физикой в ​​пределах T поверхности Ферми. ... Звезда будет быстро остывать до тех пор, пока ее внутренняя температура не станет T  <  T c  ~ ∆ , после чего ядро ​​кварковой материи станет инертным, а дальнейшая история охлаждения будет определяться испусканием нейтрино из ядерной фракции материи звезды.
  56. ^ Уолтер Левин; Уоррен Голдштейн (2011). "Рентгеновские всплески!". Из любви к физике. Саймон и Шустер. С. 251 и далее. ISBN 978-1-4391-0827-7.
  57. ^ TE Strohmayer (2006). "Структура нейтронной звезды и фундаментальная физика". В John W. Mason (ред.). Astrophysics update, Volume 2. Birkhäuser. стр. 41. ISBN 978-3-540-30312-1.

Библиография

Внешние ссылки