Нарушение симметрии

Физический процесс, переводящий систему из симметричного состояния в более упорядоченное состояние.

Мяч изначально находится на вершине центрального холма (C). Это положение является неустойчивым равновесием: очень небольшое возмущение заставит его упасть в одну из двух устойчивых ям слева (L) или справа (R). Даже если холм симметричен и нет причин для падения мяча на какую-либо сторону, наблюдаемое конечное состояние не является симметричным.

В физике нарушение симметрии — это явление, при котором неупорядоченное , но симметричное состояние коллапсирует в упорядоченное, но менее симметричное состояние. ^[1] Этот коллапс часто является одной из многих возможных бифуркаций , которые может предпринять частица при приближении к более низкому энергетическому состоянию. Из-за множества возможностей наблюдатель может предположить, что результат коллапса будет произвольным. Это явление является фундаментальным для квантовой теории поля (КТП) и, кроме того, для современного понимания физики . ^[2] В частности, оно играет центральную роль в модели Глэшоу–Вайнберга–Салама , которая является частью Стандартной модели, моделирующей электрослабый сектор.

(Черная) частица всегда стремится к самой низкой энергии. В предлагаемой -симметричной системе она имеет два возможных (фиолетовых) состояния. Когда она спонтанно нарушает симметрию, она коллапсирует в одно из двух состояний. Это явление известно как спонтанное нарушение симметрии. ${\displaystyle \mathbb {Z} _{2}}$

Трехмерное изображение частицы в симметричной системе ( механизм Хиггса ) до перехода в состояние с более низкой энергией.

В бесконечной системе ( пространство-время Минковского ) происходит нарушение симметрии, однако в конечной системе (то есть любой реальной сверхконденсированной системе) система менее предсказуема, но во многих случаях происходит квантовое туннелирование . ^{[2] [3]} Нарушение симметрии и туннелирование связаны через коллапс частицы в несимметричное состояние, когда она стремится к более низкой энергии. ^[4]

Нарушение симметрии можно разделить на два типа: явное и спонтанное . Они характеризуются тем, что уравнения движения не являются инвариантными, или основное состояние не является инвариантным.

Нетехническое описание

В этом разделе описывается спонтанное нарушение симметрии. Это идея о том, что для физической системы конфигурация с самой низкой энергией ( вакуумное состояние ) не является самой симметричной конфигурацией системы. Грубо говоря, существует три типа симметрии, которые могут быть нарушены: дискретная, непрерывная и калибровочная, упорядоченные по возрастанию технической сложности.

Пример системы с дискретной симметрией представлен на рисунке с красным графиком: рассмотрим частицу, движущуюся по этому графику под действием силы тяжести . Похожий график может быть задан функцией . Эта система симметрична относительно отражения относительно оси y. Для частицы существует три возможных стационарных состояния: вершина холма в точке или дно в точке . Когда частица находится наверху, конфигурация соблюдает симметрию отражения: частица остается на том же месте при отражении. Однако конфигурации с самой низкой энергией — это конфигурации в точке . Когда частица находится в любой из этих конфигураций, она больше не фиксирована относительно отражения относительно оси y: отражение меняет местами два вакуумных состояния. ${\displaystyle f(x)=(x^{2}-a^{2})^{2}}$ ${\displaystyle x=0}$ ${\displaystyle x=\pm a}$ ${\displaystyle x=\pm a}$

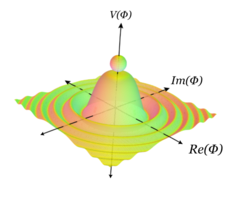
Пример с непрерывной симметрией дается трехмерным аналогом предыдущего примера, из вращения графика вокруг оси, проходящей через вершину холма, или эквивалентно заданного графиком . Это по сути график потенциала мексиканской шляпы . Он имеет непрерывную симметрию, заданную вращением вокруг оси, проходящей через вершину холма (а также дискретную симметрию путем отражения через любую радиальную плоскость). Опять же, если частица находится на вершине холма, она зафиксирована при вращениях, но имеет более высокую гравитационную энергию наверху. Внизу она больше не инвариантна при вращениях, но минимизирует свою гравитационную потенциальную энергию. Кроме того, вращения перемещают частицу из одной конфигурации, минимизирующей энергию, в другую. Здесь есть новизна, не замеченная в предыдущем примере: из любого из вакуумных состояний можно получить доступ к любому другому вакуумному состоянию с небольшим количеством энергии, двигаясь вокруг желоба у подножия холма, тогда как в предыдущем примере, чтобы получить доступ к другому вакууму, частице пришлось бы пересечь холм, что потребовало бы большого количества энергии. ${\displaystyle f(x,y)=(x^{2}+y^{2}-a^{2})^{2}}$

Нарушение калибровочной симметрии является наиболее тонким, но имеет важные физические последствия. Грубо говоря, для целей этого раздела калибровочная симметрия — это назначение систем с непрерывной симметрией каждой точке пространства-времени . Калибровочная симметрия запрещает генерацию массы для калибровочных полей , однако были обнаружены массивные калибровочные поля ( W- и Z-бозоны ). Спонтанное нарушение симметрии было разработано для разрешения этого несоответствия. Идея состоит в том, что на ранней стадии развития Вселенной она находилась в состоянии высокой энергии, аналогичном состоянию частицы на вершине холма, и поэтому имела полную калибровочную симметрию, а все калибровочные поля были безмассовыми. По мере охлаждения она перешла в выбор вакуума, таким образом спонтанно нарушив симметрию, тем самым удалив калибровочную симметрию и позволив этим калибровочным полям генерацию массы. Полное объяснение является весьма техническим: см. электрослабое взаимодействие .

Спонтанное нарушение симметрии

При спонтанном нарушении симметрии (СНС) уравнения движения системы инвариантны, но любое состояние вакуума (состояние с наименьшей энергией) — нет.

Для примера с двойной симметрией, если есть некоторый атом, который имеет два вакуумных состояния, занятие любого из этих состояний нарушает двойную симметрию. Этот акт выбора одного из состояний, когда система достигает более низкой энергии, называется SSB. Когда это происходит, атом больше не является симметричным (отражательно симметричным) и коллапсирует в состояние с более низкой энергией. ${\displaystyle \mathbb {Z} _{2}}$

Такое нарушение симметрии параметризуется параметром порядка . Частным случаем этого типа нарушения симметрии является динамическое нарушение симметрии .

В лагранжевом контексте квантовой теории поля (КТП) лагранжиан является функционалом квантовых полей, который инвариантен относительно действия группы симметрии . Однако вакуумное ожидание , образованное при коллапсе частицы до более низкой энергии, может не быть инвариантным относительно . В этом случае он частично нарушит симметрию , в подгруппу . Это спонтанное нарушение симметрии. ${\displaystyle L}$ ${\displaystyle G}$ ${\displaystyle G}$ ${\displaystyle G}$ ${\displaystyle H}$

Однако в контексте калибровочной симметрии SSB — это явление, посредством которого калибровочные поля «приобретают массу», несмотря на калибровочную инвариантность, которая требует, чтобы такие поля были безмассовыми. Это происходит потому, что SSB калибровочной симметрии нарушает калибровочную инвариантность, и такой разрыв допускает существование массивных калибровочных полей. Это важное исключение из теоремы Голдстоуна , где бозон Намбу-Голдстоуна может получить массу, становясь в процессе бозоном Хиггса . ^[5]

Кроме того, в этом контексте использование термина «нарушение симметрии», хотя и является стандартным, является неправильным, поскольку калибровочная «симметрия» на самом деле не является симметрией, а избыточностью в описании системы. Математически эта избыточность является выбором тривиализации , в некоторой степени аналогичной избыточности, возникающей из выбора базиса.

Спонтанное нарушение симметрии также связано с фазовыми переходами . Например, в модели Изинга , когда температура системы падает ниже критической температуры, симметрия вакуума нарушается, что приводит к фазовому переходу системы. ${\displaystyle \mathbb {Z} _{2}}$

Явное нарушение симметрии

Релятивистские поправки тонкой структуры (Дирак) к модели Бора атома водорода нарушают симметрии и расщепляют вырожденные уровни. Линия Лайман-альфа (испускаемая при переходе от n = 2 к n = 1) расщепляется на дублет.

При явном нарушении симметрии (ESB) уравнения движения , описывающие систему, являются вариантными при нарушенной симметрии. В гамильтоновой механике или лагранжевой механике это происходит, когда в гамильтониане (или лагранжиане) есть хотя бы один член, который явно нарушает заданную симметрию.

В гамильтоновой постановке это часто изучается, когда гамильтониан можно записать . ${\displaystyle H=H_{0}+H_{\text{int}}}$

Вот 'базовый гамильтониан', который имеет некоторую явную симметрию. Более явно, он симметричен относительно действия группы (Ли) . Часто это интегрируемый гамильтониан. ${\displaystyle H_{0}}$ ${\displaystyle G}$

Это гамильтониан возмущения или взаимодействия. Он не инвариантен относительно действия . Он часто пропорционален малому, пертурбативному параметру. ${\displaystyle H_{\text{int}}}$ ${\displaystyle G}$

Это по сути парадигма теории возмущений в квантовой механике. Примером ее использования является нахождение тонкой структуры атомных спектров.

Примеры

Нарушение симметрии может охватывать любой из следующих сценариев:

• Нарушение точной симметрии основных законов физики вследствие, по-видимому, случайного образования некоторой структуры;
• Ситуация в физике, в которой минимальное энергетическое состояние имеет меньшую симметрию, чем сама система;
• Ситуации, в которых фактическое состояние системы не отражает базовые симметрии динамики, поскольку явно симметричное состояние является нестабильным (стабильность достигается за счет локальной асимметрии);
• Ситуации, в которых уравнения теории могут иметь определенные симметрии, хотя их решения могут не иметь их (симметрии «скрыты»).

Один из первых случаев нарушенной симметрии , обсуждаемых в физической литературе, связан с формой, которую принимает равномерно вращающееся тело несжимаемой жидкости в гравитационном и гидростатическом равновесии . Якоби ^[6] и вскоре Лиувилль ^[7] в 1834 году обсуждали тот факт, что трехосный эллипсоид был равновесным решением для этой задачи, когда кинетическая энергия по сравнению с гравитационной энергией вращающегося тела превышала определенное критическое значение. Осевая симметрия, представленная сфероидами Маклорена, нарушается в этой точке бифуркации. Более того, выше этой точки бифуркации и для постоянного углового момента решения, которые минимизируют кинетическую энергию, являются неосесимметричными эллипсоидами Якоби вместо сфероидов Маклорена .

Смотрите также

• механизм Хиггса
• вакуум КХД
• 1964 PRL статьи о нарушении симметрии

Ссылки

1. Хейлиген, Фрэнсис (2023). «Запутывание, нарушение симметрии и коллапс: соответствия между квантовой и самоорганизующейся динамикой». Foundations of Science . 28. Брюссель, Бельгия: 85–107. doi :10.1007/s10699-021-09780-7. S2CID  4568832 – через SpringerLink.
2. Gross, David J. (1996-12-10). «Роль симметрии в фундаментальной физике». PNAS . 93 (25): 14256–14259. doi : 10.1073/pnas.93.25.14256 . PMC 34470 . PMID  11607718. 
3. Охира, Рютаро; Мукайяма, Такаши; Тоёда, Кэндзи (2020-02-01). «Нарушение вращательной симметрии в квантовом туннельном роторе с захваченными ионами». Physical Review A. 101 ( 2). Американское физическое общество : 022106. arXiv : 1907.07404 . Bibcode : 2020PhRvA.101b2106O. doi : 10.1103/PhysRevA.101.022106.
4. Кастеллани, Елена; Тех, Николас; Брэдинг, Кэтрин (14.12.2017). Эдвард, Залта (ред.). «Симметрия и нарушение симметрии». Стэнфордская энциклопедия философии (ред. осень 2021 г.). Исследовательская лаборатория метафизики, Стэнфордский университет.
5. Лоу, Джонатан; Ренни, Ричард (2009). "Теорема Голдстоуна". Словарь физики (6-е изд.). Oxford University Press . doi :10.1093/acref/9780199233991.001.0001. ISBN 9780199233991. Получено 2023-03-01 .
6. Якоби, CGJ (1834). «Über die figur des gleichgewichts». Аннален дер Физик и Химия . 109 (33): 229–238. Бибкод : 1834AnP...109..229J. дои : 10.1002/andp.18341090808.
7. Лиувилл, Дж. (1834). «Сюр ла фигура массовой жидкости однородна, в равновесии и в двойном движении вращения». Журнал Политехнической школы (14): 289–296.

Внешние ссылки

• Цитаты, связанные с нарушением симметрии в Wikiquote