Архимедова спираль

Спираль с постоянным расстоянием от себя

Три 360° петли одного плеча архимедовой спирали

Архимедова спираль (также известная как спираль Архимеда , арифметическая спираль ) — спираль, названная в честь греческого математика III века до н. э. Архимеда . Термин «архимедова спираль» иногда используется для обозначения более общего класса спиралей этого типа (см. ниже), в отличие от спирали Архимеда (конкретной арифметической спирали Архимеда). Это геометрическое место , соответствующее местоположению с течением времени точки, удаляющейся от фиксированной точки с постоянной скоростью вдоль линии, которая вращается с постоянной угловой скоростью . Эквивалентно, в полярных координатах ( r , θ ) она может быть описана уравнением с действительным числом b . Изменение параметра b управляет расстоянием между петлями. $${\displaystyle r=b\cdot \theta }$$

Таким образом, из приведенного выше уравнения можно заключить: положение частицы от точки старта пропорционально углу θ с течением времени.

Архимед описал такую ​​спираль в своей книге «О спиралях» . Конон Самосский был его другом, и Папп утверждает, что эта спираль была открыта Кононом. ^[1]

Вывод общего уравнения спирали

Ниже используется физический подход для понимания понятия архимедовых спиралей.

Предположим, что точечный объект движется в декартовой системе с постоянной скоростью v, направленной параллельно оси x , относительно плоскости xy . Пусть в момент времени t = 0 объект находился в произвольной точке ( c , 0, 0) . Если плоскость xy вращается с постоянной угловой скоростью ω вокруг оси z , то скорость точки относительно оси z можно записать как:

Плоскость xy поворачивается на угол ωt (против часовой стрелки) вокруг начала координат за время t . ( c , 0) — положение объекта в момент времени t = 0. P — положение объекта в момент времени t на расстоянии R = vt + c .

$${\displaystyle {\begin{aligned}|v_{0}|&={\sqrt {v^{2}+\omega ^{2}(vt+c)^{2}}}\\v_{x}&=v\cos \omega t-\omega (vt+c)\sin \omega t\\v_{y}&=v\sin \omega t+\omega (vt+c)\cos \omega t\end{aligned}}}$$

Как показано на рисунке рядом, vt + c представляет собой модуль радиус- вектора частицы в любой момент времени t , причем v _x и v _y являются компонентами скорости вдоль осей x и y соответственно.

$${\displaystyle {\begin{aligned}\int v_{x}\,dt&=x\\\int v_{y}\,dt&=y\end{aligned}}}$$

Приведенные выше уравнения можно интегрировать, применяя интегрирование по частям , что приводит к следующим параметрическим уравнениям:

$${\displaystyle {\begin{aligned}x&=(vt+c)\cos \omega t\\y&=(vt+c)\sin \omega t\end{aligned}}}$$

Возведение двух уравнений в квадрат и последующее сложение (и некоторые небольшие изменения) приводит к декартову уравнению (используя тот факт, что ωt = θ и θ = arctan ⁠ $${\displaystyle {\sqrt {x^{2}+y^{2}}}={\frac {v}{\omega }}\cdot \arctan {\frac {y}{x}}+c}$$у/х⁠ ) ​​или $${\displaystyle \tan \left(\left({\sqrt {x^{2}+y^{2}}}-c\right)\cdot {\frac {\omega }{v}}\right)={\frac {y}{x}}}$$

Его полярная форма - $${\displaystyle r={\frac {v}{\omega }}\cdot \theta +c.}$$

Длина и кривизна дуги

Соприкасающиеся окружности архимедовой спирали, касающиеся спирали и имеющие одинаковую кривизну в точке касания. Сама спираль не нарисована, но ее можно увидеть в точках, где окружности особенно близки друг к другу.

Учитывая параметризацию в декартовых координатах, длина дуги от θ ₁ до θ ₂ равна или, что эквивалентно: Общая длина от θ ₁ = 0 до θ ₂ = θ равна, следовательно, $${\displaystyle f\colon \theta \mapsto (r\,\cos \theta ,r\,\sin \theta )=(b\,\theta \,\cos \theta ,b\,\theta \,\sin \theta )}$$ $${\displaystyle {\frac {b}{2}}\left[\theta \,{\sqrt {1+\theta ^{2}}}+\ln \left(\theta +{\sqrt {1+\theta ^{2}}}\right)\right]_{\theta _{1}}^{\theta _{2}}}$$ $${\displaystyle {\frac {b}{2}}\left[\theta \,{\sqrt {1+\theta ^{2}}}+\operatorname {arsinh} \theta \right]_{\theta _{1}}^{\theta _{2}}.}$$ $${\displaystyle {\frac {b}{2}}\left[\theta \,{\sqrt {1+\theta ^{2}}}+\ln \left(\theta +{\sqrt {1+\theta ^{2}}}\right)\right].}$$

Кривизна определяется как $${\displaystyle \kappa ={\frac {\theta ^{2}+2}{b\left(\theta ^{2}+1\right)^{\frac {3}{2}}}}}$$

Характеристики

Архимедова спираль, представленная на полярном графике

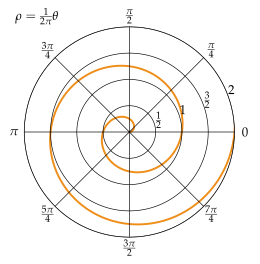
Архимедова спираль обладает тем свойством, что любой луч из начала координат пересекает последовательные повороты спирали в точках с постоянным разделительным расстоянием (равным 2πb , если θ измеряется в радианах ), отсюда и название «арифметическая спираль». В отличие от этого, в логарифмической спирали эти расстояния, а также расстояния точек пересечения, измеренные от начала координат, образуют геометрическую прогрессию .

Архимедова спираль имеет два рукава, один для θ > 0 и один для θ < 0. Два рукава плавно соединены в начале координат. На прилагаемом графике показан только один рукав. Зеркальное отображение этого рукава по оси y даст другой рукав.

При больших θ точка движется с хорошо аппроксимируемым равномерным ускорением по архимедовой спирали, в то время как спираль соответствует положениям во времени точки, удаляющейся от фиксированной точки с постоянной скоростью вдоль линии, которая вращается с постоянной угловой скоростью ^[2] (см. статью Михаила Гайченкова).

По мере роста архимедовой спирали ее эволюта асимптотически приближается к окружности с радиусом ⁠| в |/ω⁠ .

Общая архимедова спираль

Иногда термин «архимедова спираль» используется для более общей группы спиралей. $${\displaystyle r=a+b\cdot \theta ^{\frac {1}{c}}.}$$

Обычная архимедова спираль возникает при c = 1. Другие спирали, попадающие в эту группу, включают гиперболическую спираль ( c = −1 ), спираль Ферма ( c = 2 ) и литуус ( c = −2 ).

Приложения

Один из методов квадратуры круга , предложенный Архимедом, использует архимедову спираль. Архимед также показал, как спираль может быть использована для трисекции угла . Оба подхода смягчают традиционные ограничения на использование линейки и циркуля в древнегреческих геометрических доказательствах. ^[3]

Механизм спирального компрессора

Архимедова спираль имеет множество реальных применений. Спиральные компрессоры , используемые для сжатия газов, имеют роторы, которые могут быть сделаны из двух чередующихся архимедовых спиралей, эвольвент окружности одинакового размера, которые почти напоминают архимедовы спирали, ^[4] или гибридных кривых.

Архимедовы спирали можно найти в спиральной антенне , которая может работать в широком диапазоне частот.

Витки пружин баланса часов и канавки самых ранних граммофонных пластинок образуют архимедовы спирали, благодаря чему канавки располагаются равномерно (хотя позже был введен переменный интервал между дорожками, чтобы максимизировать объем музыки, которую можно было записать на пластинку). ^[5]

Попросив пациента нарисовать спираль Архимеда, можно количественно оценить тремор человека ; эта информация помогает в диагностике неврологических заболеваний.

Архимедовы спирали также используются в проекционных системах цифровой обработки света (DLP) для минимизации « эффекта радуги », создавая впечатление, что несколько цветов отображаются одновременно, тогда как на самом деле красный, зеленый и синий циклически сменяют друг друга чрезвычайно быстро. ^[6] Кроме того, Архимедовы спирали используются в пищевой микробиологии для количественной оценки концентрации бактерий с помощью спиральной пластины. ^[7]

Изображение LL Pegasi, полученное с помощью большой миллиметровой решетки в Атакаме

Они также используются для моделирования узора, который возникает в рулоне бумаги или ленте постоянной толщины, обернутой вокруг цилиндра. ^{[8] [9]}

Многие динамические спирали (такие как спираль Паркера солнечного ветра или узор, созданный колесом Кэтрин ) являются архимедовыми. Например, звезда LL Пегаса демонстрирует приблизительную архимедову спираль в окружающих ее пылевых облаках, которые, как полагают, являются выброшенной из звезды материей, которая была направлена ​​в спираль другой звездой-компаньоном как часть двойной звездной системы. ^[10]

Методы строительства

Архимедову спираль нельзя точно построить традиционными методами циркуля и линейки, поскольку арифметическая спираль требует, чтобы радиус кривой постоянно увеличивался по мере увеличения угла в начале координат. Но арифметическую спираль можно построить приблизительно, с разной степенью точности, различными методами ручного черчения. Один из таких методов использует циркуль и линейку; другой метод использует модифицированный струнный циркуль.

Традиционное построение использует циркуль и линейку для аппроксимации арифметической спирали. Сначала строится большой круг, и его окружность подразделяется 12 диаметрами на 12 дуг (по 30 градусов каждый; см. правильный додекагон ). Затем радиус этого круга сам подразделяется на 12 единичных сегментов (радиальных единиц), и строится ряд концентрических окружностей, каждая с радиусом, увеличенным на одну радиальную единицу. Начиная с горизонтального диаметра и самой внутренней концентрической окружности, отмечается точка, где ее радиус пересекает ее окружность; затем переходим к следующей концентрической окружности и к следующему диаметру (двигаясь вверх, чтобы построить спираль против часовой стрелки, или вниз, чтобы по часовой стрелке), чтобы отметить следующую точку. После того, как все точки отмечены, последовательные точки соединяются линией, аппроксимирующей арифметическую спираль (или плавной кривой некоторого вида; см. Французская кривая ). В зависимости от желаемой степени точности этот метод можно улучшить, увеличив размер большого внешнего круга, сделав больше подразделений как его окружности, так и радиуса, увеличив количество концентрических окружностей (см. Многоугольная спираль ). Аппроксимация спирали Архимеда этим методом, конечно, напоминает знаменитый метод Архимеда аппроксимации π путем удвоения сторон последовательных многоугольников (см. Многоугольное приближение π ).

Построение спирали Феодора с помощью циркуля и линейки — еще один простой метод аппроксимации спирали Архимеда.

Механический метод построения арифметической спирали использует модифицированный струнный циркуль, где струна оборачивается и наматывается (или разматывается/раскручивается) вокруг фиксированного центрального штифта (который не вращается), тем самым увеличивая (или уменьшая) длину радиуса (струны) по мере изменения угла (струна обматывается вокруг фиксированного штифта, который не вращается). Такой метод является простым способом создания арифметической спирали, возникающим естественным образом из-за использования струнного циркуля с намоточным штифтом (а не свободного шарнира обычного струнного циркуля). Инструмент для рисования струнного циркуля имеет различные модификации и конструкции, и этот метод построения напоминает струнные методы создания эллипсов (с двумя фиксированными штифтами).

Еще один механический метод является вариантом предыдущего метода струнного циркуля, обеспечивая большую точность и большую гибкость. Вместо центрального штифта и струны струнного циркуля, это устройство использует невращающийся вал (колонну) с винтовой резьбой (винт; см. винт Архимеда ), к которому прикреплены два прорезных рычага: один горизонтальный рычаг прикреплен (движется вверх) к винтовой резьбе вертикального вала на одном конце и удерживает чертежный инструмент на другом конце; другой наклонный рычаг прикреплен одним концом к верхней части винтового вала и соединен штифтом, свободно установленным в его пазу, с пазом горизонтального рычага. Два рычага вращаются вместе и работают в согласии, создавая арифметическую спираль: по мере того, как горизонтальный рычаг постепенно поднимается по винту, прорезное крепление этого рычага к наклонному рычагу постепенно сокращает радиус рисования. Угол наклонного рычага остается постоянным на всем протяжении (чертит конус ) , а установка другого угла изменяет шаг спирали. Это устройство обеспечивает высокую степень точности, в зависимости от точности, с которой устройство обработано (обработка точной винтовой резьбы является смежной задачей). И, конечно, использование винтового вала в этом механизме напоминает винт Архимеда .

Смотрите также

• Математический портал

• Архимедов винт  – Механизм перекачивания воды ^[11]
• Спираль Ферма  – спираль, охватывающая одинаковую площадь за один оборот.
• Золотая спираль  – Самоподобная кривая, связанная с золотым сечением.
• Гиперболическая спираль  – Спираль, асимптотическая к прямой
• Список спиралей
• Логарифмическая спираль  – Самоподобная кривая роста
• Спираль Феодора  – многоугольная кривая, образованная прямоугольными треугольниками.
• Символ тройной спирали  – Различные символы с тройной вращательной симметриейPages displaying short descriptions of redirect targets

Ссылки

1. Балмер-Томас, Айвор . «Конон Самосский». Словарь научной биографии . Т. 3. С. 391.
2. Sloane, N. J. A. (ред.). "Последовательность A091154". Онлайновая энциклопедия целочисленных последовательностей . Фонд OEIS.
3. Бойер, Карл Б. (1968). История математики . Принстон, Нью-Джерси: Princeton University Press. стр. 140–142. ISBN 0-691-02391-3.
4. Саката, Хироцугу; Окуда, Масаюки. "Устройство для сжатия жидкости с коаксиальными спиральными элементами" . Получено 25.11.2006 .
5. Пенндорф, Рон. "Раннее развитие LP". Архивировано из оригинала 5 ноября 2005 г. Получено 25 ноября 2005 г.. См. отрывок о переменной канавке .
6. Баллу, Глен (2008), Справочник для звукорежиссеров, CRC Press, стр. 1586, ISBN 9780240809694
7. Gilchrist, JE; Campbell, JE; Donnelly, CB; Peeler, JT; Delaney, JM (1973). «Метод спиральной пластины для определения бактерий». Applied Microbiology . 25 (2): 244–52. doi :10.1128/AEM.25.2.244-252.1973. PMC 380780. PMID  4632851 . 
8. Перессини, Тони (3 февраля 2009 г.). "Проблема рулона бумаги Джоан" (PDF) . Архивировано из оригинала (PDF) 3 ноября 2013 г. . Получено 2014-10-06 .
9. Вальсер, Х.; Хилтон, П.; Педерсен, Дж. (2000). Симметрия . Математическая ассоциация Америки. стр. 27. ISBN 9780883855324. Получено 2014-10-06 .
10. Ким, Хёсун; Трехо, Альфонсо; Лю, Шэн-Юань; Сахай, Рагвендра; Таам, Рональд Э.; Моррис, Марк Р.; Хирано, Наоми; Хси, И-Та (март 2017 г.). "Крупномасштабная небулярная структура двойного суперветра на эксцентричной орбите". Nature Astronomy . 1 (3): 0060. arXiv : 1704.00449 . Bibcode :2017NatAs...1E..60K. doi :10.1038/s41550-017-0060. S2CID  119433782.

Внешние ссылки

• Джонатан Мэтт делает спираль Архимеда интересной - Видео: Удивительная красота математики - TedX Talks , Green Farms
• Вайсштейн, Эрик В. «Спираль Архимеда». Математический мир .
• Архимедова спираль на PlanetMath .
• Страница с Java-приложением для интерактивного изучения архимедовой спирали и связанных с ней кривых
• Онлайн-исследование с использованием JSXGraph (JavaScript)
• Архимедова спираль в "mathcurve"