
Джон Нейпир из Мерчистона ( / ˈ n eɪ p i ər / NAY -pee-ər ; [1] латинизировано как Иоанн Непер ; 1 февраля 1550 — 4 апреля 1617), по прозвищу Чудесный Мерчистон , был шотландским землевладельцем, известным как математик , физик и астроном . Он был 8-м лэрдом Мерчистона .
Джон Непер наиболее известен как первооткрыватель логарифмов . Он также изобрел так называемые « косточки Непера » и сделал общепринятым использование десятичной точки в арифметике и математике.
Место рождения Нейпира, башня Мерчистон в Эдинбурге , теперь является частью объектов Эдинбургского университета Нейпира . В церкви Св. Катберта на западной стороне Эдинбурга есть памятник ему . [2]
Отцом Нейпира был сэр Арчибальд Нейпир из замка Мерчистон, а матерью — Джанет Ботвелл, дочь политика и судьи Фрэнсиса Ботвелла [3] и сестра Адама Ботвелла , который стал епископом Оркнейских островов . Арчибальду Нейпиру было 16 лет, когда родился Джон Нейпир [3] .

Нет никаких записей о раннем обучении Нейпира, но многие полагают, что в раннем детстве он занимался с частным репетитором. В возрасте 13 лет он был зачислен в колледж Святого Сальватора в Сент-Эндрюсе . Ко времени его поступления качество образования, предоставляемого университетом, было низким, отчасти из-за того, что Реформация вызвала раздор между сторонниками старой веры и растущим числом протестантов. Нет никаких записей, подтверждающих, что Джон Нейпир закончил свое образование в Сент-Эндрюсе. [4] Считается, что он покинул Шотландию, чтобы продолжить свое образование в континентальной Европе, следуя совету, данному его дядей Адамом Ботвеллом в письме, написанном отцу Джона Нейпира 5 декабря 1560 года, в котором говорилось: «Я прошу вас, сэр, отправить Джона в школы либо во Францию , либо во Фландрию , поскольку дома он не сможет научиться ничему хорошему». [5] Неизвестно, какой университет в Европе посещал Нейпир, но когда он вернулся в Шотландию в 1571 году, он свободно говорил на греческом языке, который в то время не преподавался в европейских университетах. Также нет записей, подтверждающих его зачисление в ведущие университеты Парижа или Женевы в то время. [6] [4]
В 1571 году Нейпир, которому было 21 год, вернулся в Шотландию и купил замок в Гартнессе в 1574 году. После смерти отца в 1608 году Нейпир и его семья переехали в замок Мерчистон в Эдинбурге, где он прожил остаток своей жизни. У него также была собственность в Эдинбурге на Бортвик-Клоуз у Королевской Мили . [7]

7 июня 1596 года Нейпир написал статью « Секретные изобретения, выгодные и необходимые в наши дни для обороны этого острова ». Он описывает два вида зажигательного зеркала для использования против кораблей на расстоянии, особый вид артиллерийского выстрела и металлическую колесницу, защищенную от мушкетов. [8]
Нейпир умер от подагры дома в замке Мерчистон в возрасте 67 лет. Он был похоронен на кладбище церкви Святого Джайлза в Эдинбурге. После того, как кладбище церкви Святого Джайлза было утрачено из-за строительства здания парламента , его останки были перенесены в подземное хранилище на северной стороне приходской церкви Святого Кутберта в западной части Эдинбурга. [2] Также в церкви Святого Кутберта есть настенный памятник Нейпиру. [2]
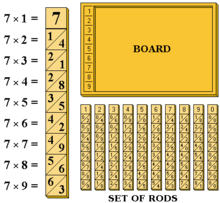
Многие математики того времени остро осознавали проблемы вычислений и стремились избавить практиков от бремени вычислений. Нейпир был известен своими устройствами, помогавшими с этими проблемами вычислений. Он изобрел известный математический артефакт, гениальные нумерационные стержни, более известные как «кости Нейпира», [9] , которые предлагали механические средства для облегчения вычислений.
Кроме того, Нейпир осознал потенциал последних достижений в математике, особенно в области простаферезиса , десятичных дробей и символической индексной арифметики, для решения проблемы сокращения вычислений. Он понимал, что в большинстве случаев практикующие специалисты, которым приходилось выполнять трудоемкие вычисления, обычно делали их в контексте тригонометрии. Поэтому, помимо разработки логарифмического соотношения, Нейпир поместил его в тригонометрический контекст, чтобы оно стало еще более релевантным.
Его работа Mirifici Logarithmorum Canonis Descriptio (1614) содержала пятьдесят семь страниц пояснительного материала и девяносто страниц таблиц, перечисляющих натуральные логарифмы тригонометрических функций . [10] : Гл. III В книге также обсуждается теорема сферической тригонометрии , обычно известная как «Правила Непера для круговых частей».
Современные английские переводы обеих книг Непера о логарифмах и их описания можно найти в Интернете, как и обсуждение костей Непера и Promptuary (еще одного раннего вычислительного устройства). [11]
Его изобретение логарифмов было быстро подхвачено в колледже Грешема , и выдающийся английский математик Генри Бриггс посетил Непера в 1615 году. Среди вопросов, которые они обсуждали, был вопрос о перемасштабировании логарифмов Непера, в котором наличие математической константы, теперь известной как e (точнее, e , умноженное на большую степень 10, округленную до целого числа), представляло практическую трудность. Ни Непер, ни Бриггс на самом деле не открыли константу e ; это открытие было сделано десятилетия спустя Якобом Бернулли .
Нейпир делегировал Бриггсу вычисление пересмотренной таблицы. Вычислительный прогресс, доступный посредством логарифмов, инверсии степенных чисел или экспоненциальной записи , был таков, что он делал вычисления вручную намного быстрее. [12] Путь был открыт для последующих научных достижений в астрономии , динамике и других областях физики .
Непер внес дальнейший вклад. Он улучшил десятичную запись Саймона Стевина , введя точку (.) в качестве разделителя дробной части. [13] : стр. 8, архив стр. 32) Решеточное умножение , используемое Фибоначчи , стало более удобным благодаря введению им костей Непера — инструмента умножения, использующего набор пронумерованных стержней.
Нейпир, возможно, работал в значительной степени в изоляции, но он контактировал с Тихо Браге , который переписывался с его другом Джоном Крейгом . Крейг, несомненно, объявил об открытии логарифмов Браге в 1590-х годах (само название появилось позже); есть история от Энтони а Вуда , возможно, не очень обоснованная, что Нейпир получил намек от Крейга, что Лонгомонтанус , последователь Браге, работал в похожем направлении. У Крейга были заметки о методе Пауля Виттиха , который использовал тригонометрические тождества для сведения формулы умножения для синусоидальной функции к сложениям. [14]

Когда один из углов, скажем C , сферического треугольника равен π /2, различные тождества, приведенные выше, значительно упрощаются. Существует десять тождеств, связывающих три элемента, выбранных из множества a , b , c , A , B .
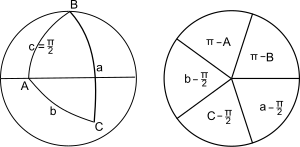
Нейпир [15] предоставил элегантную мнемоническую схему для десяти независимых уравнений: эта мнемоника называется кругом Нейпира или пятиугольником Нейпира (когда круг на рисунке выше, справа, заменен пятиугольником).
Сначала запишите шесть частей треугольника (три угла вершины, три угла дуги для сторон) в том порядке, в котором они встречаются вокруг любой цепи треугольника: для треугольника, показанного выше слева, движение по часовой стрелке, начиная с a, дает aCbAcB . Затем замените части, которые не примыкают к C (то есть A, c, B ), их дополнениями, а затем удалите угол C из списка. Оставшиеся части затем можно нарисовать как пять упорядоченных, равных частей пентаграммы или круга, как показано на рисунке выше (справа). Для любого выбора из трех смежных частей одна ( средняя часть) будет примыкать к двум частям и находиться напротив двух других частей. Десять правил Непера задаются как
Ключ к запоминанию того, какая тригонометрическая функция соответствует какой части, заключается в том, чтобы посмотреть на первую гласную вида части: средние части берут синус, соседние части берут тангенс, а противоположные части берут косинус. Например, начиная с сектора, содержащего , мы имеем:
Полный набор правил для прямоугольного сферического треугольника (Тодхантер, [16] Статья 62)
Квадрантный сферический треугольник определяется как сферический треугольник, в котором одна из сторон стягивает угол π /2 радиан в центре сферы: на единичной сфере сторона имеет длину π /2. В случае, когда сторона c имеет длину π /2 на единичной сфере, уравнения, управляющие оставшимися сторонами и углами, могут быть получены путем применения правил для прямоугольного сферического треугольника из предыдущего раздела к полярному треугольнику A'B'C' со сторонами a',b',c' такими, что A' = π − a , a' = π − A и т. д. Результаты таковы:
Логарифм
Дано положительное действительное число b, такое что b ≠ 1, логарифм положительного действительного числа x по основанию b — это показатель степени, в которую нужно возвести b, чтобы получить x . Другими словами, логарифм x по основанию b — это уникальное действительное число y, такое что b y = x .
Логарифм обозначается как «log b x » (произносится как «логарифм x по основанию b », « логарифм x по основанию b » или, чаще всего, «логарифм x по основанию b »).
Эквивалентное и более краткое определение состоит в том, что функция является обратной функцией к функции


Нейпир интересовался Книгой Откровения со студенческих лет в колледже Святого Сальватора в Сент-Эндрюсе . Под влиянием проповедей Кристофера Гудмена он развил резко антипапское чтение, доходя до того, что в некоторых своих трудах утверждал, что Папа был Антихристом. [12] [17]
Нейпир считал «A Plaine Discovery of the Whole Revelation of St. John» (1593) своей самой важной работой. Она была написана на английском языке, в отличие от других его публикаций, чтобы охватить как можно более широкую аудиторию и чтобы, по словам Нейпира, «простые этого острова могли быть наставлены». [17] «A Plaine Discovery» использовал математический анализ Книги Откровения , чтобы попытаться предсказать дату Апокалипсиса . Нейпир определил события в хронологическом порядке, которые, по его мнению, были параллелями с событиями, описанными в Книге Откровения, полагая, что структура Откровения подразумевает, что пророчества будут исполняться постепенно. [17] В этой работе Нейпир датировал седьмую трубу 1541 годом и предсказал, что конец света наступит либо в 1688, либо в 1700 году. Нейпир не верил, что люди могут знать истинную дату Апокалипсиса, но утверждал, что поскольку Библия содержит так много подсказок о конце, Бог хотел, чтобы Церковь знала, когда наступит конец. [17]
В своем посвящении Plaine Discovery Якову VI , датированном 29 января 1594 года, [18] Нейпир призвал короля увидеть, «чтобы справедливость восторжествовала против врагов Божьей церкви», и посоветовал королю «исправить всеобщие чудовищности его страны, и в первую очередь начать с его собственного дома, семьи и двора». Том включает девять страниц английских стихов Нейпира. Он имел успех на родине и за рубежом. В 1600 году Мишель Паннель сделал голландский перевод, и он вышел во втором издании в 1607 году. В 1602 году работа появилась в Ла-Рошели во французской версии Жоржа Томсона, пересмотренной Нейпиром, и также выдержавшей несколько изданий (1603, 1605 и 1607). Новое издание английского оригинала потребовалось в 1611 году, когда оно было пересмотрено и исправлено автором, и расширено добавлением With a resolution of certain doubts, moved by some well affected brothers. ; [19] оно появилось одновременно в Эдинбурге и Лондоне. Автор заявил, что он все еще намеревался опубликовать латинское издание, но оно так и не появилось. Немецкий перевод первой части работы Непера, выполненный Лео де Дромной, появился в Гере в 1611 году, а всего произведения — Вольфгангом Мейером во Франкфурте-на-Майне в 1615 году. [12] Среди последователей Непера был Мэтью Коттьер ( Matthieu Cottière ). [20]
В дополнение к своим математическим и религиозным интересам, Нейпир часто воспринимался как маг, и, как полагают, он занимался алхимией и некромантией . Говорили, что он путешествовал с черным пауком в маленькой коробке, и что его черный петух был его духом-помощником . [21] [22] [23]
Некоторые из соседей Нейпира обвиняли его в том, что он колдун и в сговоре с дьяволом, полагая, что все время, которое он проводил в своем кабинете, использовалось для изучения черного искусства. Эти слухи были подогреты, когда Нейпир использовал своего черного петуха, чтобы поймать вора. Нейпир приказал своим слугам пойти в темную комнату и погладить петуха, утверждая, что птица закукарекает, если они будут теми, кто украдет его имущество. Нейпир не знал, что слуги покрыли птицу сажей, и когда слуги вышли из комнаты, Нейпир осмотрел их руки, чтобы найти того, кто был слишком напуган, чтобы прикоснуться к петуху. [24]
Еще один поступок, который, как сообщается, совершил Нейпир, который мог показаться мистическим местным жителям, был, когда Нейпир удалил голубей из своего поместья, поскольку они ели его зерно. Нейпир поймал голубей, разбросав зерно, смешанное с алкоголем, по всему полю, а затем поймал голубей, когда они были слишком пьяны, чтобы улететь. [25]
До сих пор существует контракт на поиск сокровищ , заключенный между Нейпиром и Робертом Логаном из Ресталрига . Нейпир должен был обыскать замок Фаст-Касл в поисках сокровищ, якобы спрятанных там, в котором говорилось, что Нейпир должен «приложить все усилия для поиска и изыскания, и всеми силами и средствами обнаружить то же самое или убедиться, что ничего подобного там не было». [12] [26] Этот контракт Нейпир так и не выполнил, и никакого золота не было найдено, когда Эдинбургское археологическое полевое общество проводило раскопки замка между 1971 и 1986 годами. [26]
Среди ранних последователей Непера были производители инструментов Эдмунд Гюнтер и Джон Шпейделл . [27] [28] [29] Развитие логарифмов считается крупнейшим фактором в общем принятии десятичной арифметики . [30] « Триссотетры » (1645) Томаса Уркухарта основаны на работах Непера по тригонометрии . [31]
Генри Бриггс был одним из первых, кто принял логарифм Непера. Позже он вычислил новую таблицу логарифмов по основанию 10 с точностью до 14 знаков после запятой. [32]
Альтернативная единица измерения децибела, используемая в электротехнике , непер , названа в честь Нейпира, как и Эдинбургский университет Нейпира в Эдинбурге, Шотландия.
В его честь назван кратер Непер на Луне. [33]
На французском, испанском и португальском языках натуральный логарифм назван в его честь (соответственно, Logarithme Népérien и Logaritmos Neperianos на испанском и португальском языках). На финском и итальянском языках математическая константа e названа в его честь ( Neperin luku и Numero di Nepero ).
В 1572 году Нейпир женился на 16-летней Элизабет, дочери Джеймса Стерлинга, 4-го лэрда Кейра и Кэддера . [34] У них было двое детей. Элизабет умерла в 1579 году, и Нейпир затем женился на Агнес Чисхолм, с которой у него было еще десять детей.
Тесть Нейпира, сэр Джеймс Чисхолм из Кромликса, был одним из многих, отлученных Генеральной Ассамблеей пресвитерианской партии после испанского заговора с пустыми ящиками . Нейпир заседал в Генеральной Ассамблее, которая отлучила заговорщиков, и подал прошение королю Якову VI и I о наказании заговорщиков, но в конечном итоге его прошение было проигнорировано, поскольку король считал, что министры действовали жестоко, и выступал за проведение политики большего умиротворения. [17] [35]
Его единокровным братом (от повторного брака отца) был Александр Нейпир, лорд Лористон .
{{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка ) CS1 maint: числовые имена: список авторов ( ссылка ){{cite book}}: CS1 maint: местоположение отсутствует издатель ( ссылка ) CS1 maint: несколько имен: список авторов ( ссылка ) CS1 maint: числовые имена: список авторов ( ссылка )В числах, различаемых таким образом точкой в середине, все, что написано после точки, является дробью, знаменатель которой – единица со столькими цифрами после нее, сколько цифр после точки.
{{cite book}}: CS1 maint: местоположение отсутствует издатель ( ссылка ) CS1 maint: несколько имен: список авторов ( ссылка ) CS1 maint: числовые имена: список авторов ( ссылка ){{cite book}}: CS1 maint: местоположение отсутствует издатель ( ссылка ) CS1 maint: несколько имен: список авторов ( ссылка ) CS1 maint: числовые имена: список авторов ( ссылка )Атрибуция