Функция Кантора

Непрерывная функция, которая не является абсолютно непрерывной

График функции Кантора на единичном интервале

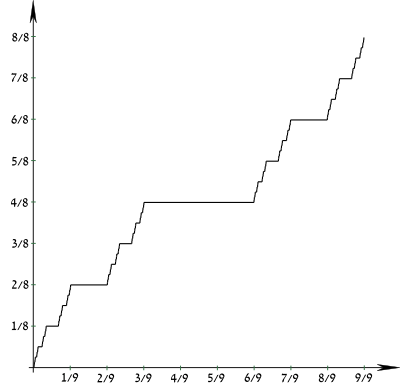
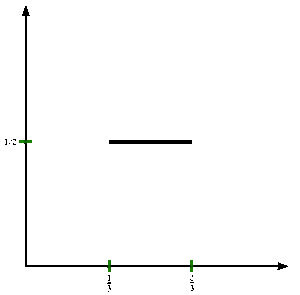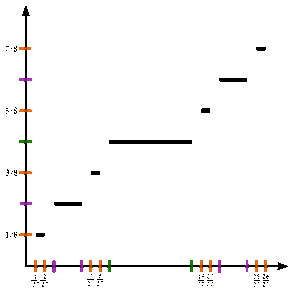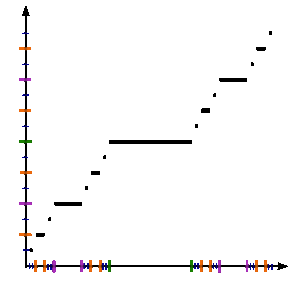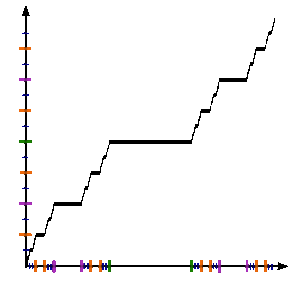
В математике функция Кантора является примером функции , которая является непрерывной , но не абсолютно непрерывной . Это печально известный контрпример в анализе, потому что он бросает вызов наивным интуициям о непрерывности, производной и мере . Хотя она непрерывна везде и имеет нулевую производную почти везде, ее значение все еще меняется от 0 до 1, когда ее аргумент достигает значения от 0 до 1. Таким образом, в одном смысле функция кажется очень похожей на константу, которая не может расти, а в другом — она действительно монотонно растет.

Её также называют тернарной функцией Кантора , функцией Лебега , ^[1] сингулярной функцией Лебега , функцией Кантора–Витали , дьявольской лестницей , ^[2] функцией лестницы Кантора , [ ^3] и функцией Кантора–Лебега . ^[4] Георг Кантор  (1884) ввёл функцию Кантора и упомянул, что Шеффер указал на то, что она является контрпримером к расширению фундаментальной теоремы исчисления, заявленной Гарнаком . Функция Кантора обсуждалась и популяризировалась Шеффером (1884), Лебегом (1904) и Витали (1905).

Определение

Итеративное построение функции Кантора

Чтобы определить функцию Кантора , пусть будет любым числом из и получим, выполнив следующие шаги: ${\displaystyle c:[0,1]\to [0,1]}$ ${\displaystyle x}$ ${\displaystyle [0,1]}$ ${\displaystyle c(x)}$

1. Выразите в системе счисления с основанием 3, используя цифры 0, 1, 2. ${\displaystyle x}$
2. Если представление числа в системе с основанием 3 содержит 1, замените каждую цифру строго после первой 1 на 0. ${\displaystyle x}$
3. Замените оставшиеся двойки единицами.
4. Интерпретировать результат как двоичное число. Результат: . ${\displaystyle c(x)}$

Например:

• ${\displaystyle {\tfrac {1}{4}}}$имеет троичное представление 0,02020202... Единиц нет, поэтому следующим этапом по-прежнему будет 0,02020202... Это переписывается как 0,01010101... Это двоичное представление , поэтому . ${\displaystyle {\tfrac {1}{3}}}$ ${\displaystyle c({\tfrac {1}{4}})={\tfrac {1}{3}}}$
• ${\displaystyle {\tfrac {1}{5}}}$имеет троичное представление 0,01210121... Цифры после первой 1 заменяются нулями, чтобы получить 0,01000000... Это не переписывается, поскольку в нем нет двоек. Это двоичное представление , поэтому . ${\displaystyle {\tfrac {1}{4}}}$ ${\displaystyle c({\tfrac {1}{5}})={\tfrac {1}{4}}}$
• ${\displaystyle {\tfrac {200}{243}}}$имеет троичное представление 0,21102 (или 0,211012222...). Цифры после первой 1 заменяются нулями, чтобы получить 0,21. Это переписывается как 0,11. Это двоичное представление , поэтому . ${\displaystyle {\tfrac {3}{4}}}$ ${\displaystyle c({\tfrac {200}{243}})={\tfrac {3}{4}}}$

Эквивалентно, если — множество Кантора на [0,1], то функцию Кантора можно определить как ${\displaystyle {\mathcal {C}}}$ ${\displaystyle c:[0,1]\to [0,1]}$

${\displaystyle c(x)={\begin{cases}\sum _{n=1}^{\infty }{\frac {a_{n}}{2^{n}}},&x=\sum _{n=1}^{\infty }{\frac {2a_{n}}{3^{n}}}\in {\mathcal {C}}\ \mathrm {for} \ a_{n}\in \{0,1\};\\\sup _{y\leq x,\,y\in {\mathcal {C}}}c(y),&x\in [0,1]\smallsetminus {\mathcal {C}}.\end{cases}}}$

Эта формула хорошо определена, поскольку каждый член множества Кантора имеет уникальное представление с основанием 3, которое содержит только цифры 0 или 2. (Для некоторых членов троичное разложение повторяется с конечными 2, и существует альтернативное неповторяющееся разложение, заканчивающееся на 1. Например, = 0,1 ₃ = 0,02222... ₃ является членом множества Кантора). Поскольку и , и монотонно на , ясно, что также справедливо для всех . ${\displaystyle {\mathcal {C}}}$ ${\displaystyle {\tfrac {1}{3}}}$ ${\displaystyle c(0)=0}$ ${\displaystyle c(1)=1}$ ${\displaystyle c}$ ${\displaystyle {\mathcal {C}}}$ ${\displaystyle 0\leq c(x)\leq 1}$ ${\displaystyle x\in [0,1]\smallsetminus {\mathcal {C}}}$

Характеристики

Функция Кантора бросает вызов наивным интуициям о непрерывности и мере ; хотя она непрерывна всюду и имеет нулевую производную почти всюду , изменяется от 0 до 1 при изменении от 0 до 1 и принимает все значения между ними. Функция Кантора является наиболее часто цитируемым примером действительной функции, которая равномерно непрерывна (точнее, она непрерывна по Гёльдеру с показателем α  = log 2/log 3), но не абсолютно непрерывна . Она постоянна на интервалах вида (0. x ₁ x ₂ x ₃ ... x _n 022222..., 0. x ₁ x ₂ x ₃ ... x _n 200000...), и каждая точка, не входящая в множество Кантора, находится в одном из этих интервалов, поэтому ее производная равна 0 вне множества Кантора. С другой стороны, она не имеет производной ни в одной точке несчетного подмножества множества Кантора, содержащего конечные точки интервала, описанные выше. ${\textstyle c(x)}$ ${\textstyle x}$

Функцию Кантора можно также рассматривать как кумулятивную функцию распределения вероятностей меры Бернулли 1/2-1/2 μ, поддерживаемую на множестве Кантора: . Это распределение вероятностей, называемое распределением Кантора , не имеет дискретной части. То есть соответствующая мера является безатомной . Вот почему в функции нет скачков непрерывности; любой такой скачок будет соответствовать атому в мере. ${\textstyle c(x)=\mu ([0,x])}$

Однако никакая непостоянная часть функции Кантора не может быть представлена ​​как интеграл функции плотности вероятности ; интегрирование любой предполагаемой функции плотности вероятности , которая не равна нулю почти везде, по любому интервалу даст положительную вероятность для некоторого интервала, которому это распределение присваивает вероятность ноль. В частности, как указал Витали (1905), функция не является интегралом своей производной, хотя производная существует почти везде.

Функция Кантора является стандартным примером сингулярной функции .

Функция Кантора также является стандартным примером функции с ограниченной вариацией , но, как упоминалось выше, не является абсолютно непрерывной. Однако каждая абсолютно непрерывная функция является непрерывной с ограниченной вариацией.

Функция Кантора не убывает, и поэтому, в частности, ее график определяет спрямляемую кривую . Шеффер (1884) показал, что длина дуги ее графика равна 2. Обратите внимание, что график любой неубывающей функции такой, что и имеет длину, не превышающую 2. В этом смысле функция Кантора экстремальна. ${\displaystyle f(0)=0}$ ${\displaystyle f(1)=1}$

Отсутствие абсолютной преемственности

Поскольку мера Лебега несчетно бесконечного множества Кантора равна 0, для любых положительных ε  < 1 и δ существует конечная последовательность попарно непересекающихся подынтервалов с общей длиной <  δ , на которых функция Кантора кумулятивно возрастает более чем на  ε .

На самом деле, для любого δ  > 0 существует конечное число попарно непересекающихся интервалов ( x _k , y _k ) (1 ≤  k  ≤  M ) с и . ${\displaystyle \sum \limits _{k=1}^{M}(y_{k}-x_{k})<\delta }$ ${\displaystyle \sum \limits _{k=1}^{M}(c(y_{k})-c(x_{k}))=1}$

Альтернативные определения

Итеративное строительство

Ниже мы определяем последовательность { f _n } функций на единичном интервале, которая сходится к функции Кантора.

Пусть f0 ( _x ) = x .

Тогда для каждого целого числа n ≥ 0 следующая функция f _{n +1} ( x ) будет определяться через f _n ( x ) следующим образом:

Пусть f _{n +1} ( x ) = 1/2 × f _n (3 x ) , когда 0 ≤ x ≤ 1/3  ;

Пусть f _{n +1} ( x ) = 1/2, когда 1/3 ≤ x ≤ 2/3  ;

Пусть f _{n +1} ( x ) = 1/2 + 1/2 × f _n (3  x − 2) , где 2/3 ≤ x ≤ 1 .

Три определения совместимы в конечных точках 1/3 и 2/3, поскольку f _n (0) = 0 и f _n (1) = 1 для каждого  n , по индукции. Можно проверить, что f _n сходится поточечно к функции Кантора, определенной выше. Более того, сходимость равномерна. Действительно, разделяя на три случая, согласно определению f _{n +1} , можно увидеть, что

${\displaystyle \max _{x\in [0,1]}|f_{n+1}(x)-f_{n}(x)|\leq {\frac {1}{2}}\,\max _{x\in [0,1]}|f_{n}(x)-f_{n-1}(x)|,\quad n\geq 1.}$

Если f обозначает предельную функцию, то для любого n  ≥ 0

${\displaystyle \max _{x\in [0,1]}|f(x)-f_{n}(x)|\leq 2^{-n+1}\,\max _{x\in [0,1]}|f_{1}(x)-f_{0}(x)|.}$

Фрактальный объем

Функция Кантора тесно связана с множеством Кантора . Множество Кантора C можно определить как множество тех чисел в интервале [0, 1], которые не содержат цифру 1 в своем разложении по основанию 3 (триадическом) , за исключением случаев, когда за 1 следуют только нули (в этом случае хвост 1000 можно заменить на 0222, чтобы избавиться от любой 1). Оказывается, что множество Кантора является фракталом с (несчетно) бесконечным числом точек (нульмерный объем), но нулевой длиной (одномерный объем). Только D -мерный объем (в смысле меры Хаусдорфа ) принимает конечное значение, где — фрактальная размерность C. Мы можем определить функцию Кантора альтернативно как D -мерный объем сечений множества Кантора ${\displaystyle \ldots }$ ${\displaystyle \ldots }$ ${\displaystyle H_{D}}$ ${\displaystyle D=\log(2)/\log(3)}$

${\displaystyle f(x)=H_{D}(C\cap (0,x)).}$

Самоподобие

Функция Кантора обладает несколькими симметриями . Для существует симметрия отражения ${\displaystyle 0\leq x\leq 1}$

${\displaystyle c(x)=1-c(1-x)}$

и пара увеличений, одно слева и одно справа:

${\displaystyle c\left({\frac {x}{3}}\right)={\frac {c(x)}{2}}}$

и

${\displaystyle c\left({\frac {x+2}{3}}\right)={\frac {1+c(x)}{2}}}$

Увеличения могут быть каскадными; они генерируют диадический моноид . Это демонстрируется путем определения нескольких вспомогательных функций. Определим отражение как

${\displaystyle r(x)=1-x}$

Первую самосимметрию можно выразить как

${\displaystyle r\circ c=c\circ r}$

где символ обозначает композицию функций. То есть, и аналогично для других случаев. Для левого и правого увеличения запишите левые отображения ${\displaystyle \circ }$ ${\displaystyle (r\circ c)(x)=r(c(x))=1-c(x)}$

${\displaystyle L_{D}(x)={\frac {x}{2}}}$и ${\displaystyle L_{C}(x)={\frac {x}{3}}}$

Тогда функция Кантора подчиняется

${\displaystyle L_{D}\circ c=c\circ L_{C}}$

Аналогично, определите правильные отображения как

${\displaystyle R_{D}(x)={\frac {1+x}{2}}}$и ${\displaystyle R_{C}(x)={\frac {2+x}{3}}}$

Затем, аналогично,

${\displaystyle R_{D}\circ c=c\circ R_{C}}$

Две стороны можно зеркально отразить друг на друга, т.е.

${\displaystyle L_{D}\circ r=r\circ R_{D}}$

и также,

${\displaystyle L_{C}\circ r=r\circ R_{C}}$

Эти операции могут быть сложены произвольно. Рассмотрим, например, последовательность движений влево-вправо. Добавляя индексы C и D и, для ясности, опуская оператор композиции во всех местах, кроме нескольких, получаем: ${\displaystyle LRLLR.}$ ${\displaystyle \circ }$

${\displaystyle L_{D}R_{D}L_{D}L_{D}R_{D}\circ c=c\circ L_{C}R_{C}L_{C}L_{C}R_{C}}$

Произвольные строки конечной длины в буквах L и R соответствуют двоично-рациональным числам , в том смысле, что каждое двоично-рациональное число может быть записано как для целых n и m , так и в виде конечной длины бит с Таким образом, каждое двоично-рациональное число находится во взаимно-однозначном соответствии с некоторой самосимметрией функции Кантора. ${\displaystyle y=n/2^{m}}$ ${\displaystyle y=0.b_{1}b_{2}b_{3}\cdots b_{m}}$ ${\displaystyle b_{k}\in \{0,1\}.}$

Некоторые перестановки обозначений могут сделать вышеизложенное немного более простым для выражения. Пусть и обозначают L и R. Композиция функций расширяет это до моноида , в том смысле, что можно записать и в общем случае для некоторых двоичных строк цифр A , B , где AB — это просто обычная конкатенация таких строк. Тогда диадический моноид M является моноидом всех таких конечной длины лево-правых движений. Записывая как общий элемент моноида, имеем соответствующую самосимметрию функции Кантора: ${\displaystyle g_{0}}$ ${\displaystyle g_{1}}$ ${\displaystyle g_{010}=g_{0}g_{1}g_{0}}$ ${\displaystyle g_{A}g_{B}=g_{AB}}$ ${\displaystyle \gamma \in M}$

${\displaystyle \gamma _{D}\circ c=c\circ \gamma _{C}}$

Сам диадический моноид обладает несколькими интересными свойствами. Его можно рассматривать как конечное число перемещений влево-вправо по бесконечному бинарному дереву ; бесконечно удаленные «листья» на дереве соответствуют точкам на множестве Кантора, и, таким образом, моноид также представляет собой самосимметрии множества Кантора. Фактически, большой класс часто встречающихся фракталов описывается диадическим моноидом; дополнительные примеры можно найти в статье о кривых де Рама . Другие фракталы, обладающие самоподобием, описываются другими видами моноидов. Диадический моноид сам по себе является подмоноидом модулярной группы ${\displaystyle SL(2,\mathbb {Z} ).}$

Обратите внимание, что функция Кантора имеет более чем мимолетное сходство с функцией вопросительного знака Минковского . В частности, она подчиняется тем же самым соотношениям симметрии, хотя и в измененной форме.

Обобщения

Позволять

${\displaystyle y=\sum _{k=1}^{\infty }b_{k}2^{-k}}$

— двоичное (двоичное) разложение действительного числа 0 ≤ y ≤ 1 по двоичным цифрам b _k ∈ {0,1}. Это разложение более подробно обсуждается в статье о двоичном преобразовании . Затем рассмотрим функцию

${\displaystyle C_{z}(y)=\sum _{k=1}^{\infty }b_{k}z^{k}.}$

Для z  = 1/3 обратная функция x = 2  C _1/3 ( y ) является функцией Кантора. То есть, y  =  y ( x ) является функцией Кантора. В общем случае для любого z  < 1/2 C _z ( y ) выглядит как функция Кантора, повернутая на бок, причем ширина ступеней становится шире по мере того, как z приближается к нулю.

Как упоминалось выше, функция Кантора также является кумулятивной функцией распределения меры на множестве Кантора. Различные функции Кантора, или Дьявольские лестницы, могут быть получены путем рассмотрения различных безатомных вероятностных мер, поддерживаемых множеством Кантора или другими фракталами. Хотя функция Кантора имеет производную 0 почти везде, текущие исследования сосредоточены на вопросе о размере множества точек, где верхняя правая производная отличается от нижней правой производной, в результате чего производная не существует. Этот анализ дифференцируемости обычно дается в терминах фрактальной размерности , причем размерность Хаусдорфа является наиболее популярным выбором. Это направление исследований было начато в 1990-х годах Дарстом ^[5], который показал, что размерность Хаусдорфа множества недифференцируемости функции Кантора является квадратом размерности множества Кантора, . Впоследствии Фалконер ^[6] показал, что это квадратное соотношение справедливо для всех регулярных сингулярных мер Альфорса, т.е. Позже Трошейт ^[7] получил более полную картину множества, где производная не существует для более общих нормализованных мер Гиббса, поддерживаемых на самоконформных и самоподобных множествах . ${\displaystyle (\log 2/\log 3)^{2}}$ $${\displaystyle \dim _{H}\left\{x:f'(x)=\lim _{h\to 0^{+}}{\frac {\mu ([x,x+h])}{h}}{\text{ does not exist}}\right\}=\left(\dim _{H}\operatorname {supp} (\mu )\right)^{2}}$$

Функция вопросительного знака Германа Минковского визуально отдаленно напоминает функцию Кантора, представляя собой ее «сглаженную» форму; ее можно построить, перейдя от разложения в непрерывную дробь к двоичному разложению, точно так же, как функцию Кантора можно построить, перейдя от троичного разложения к двоичному. Функция вопросительного знака обладает интересным свойством иметь нулевые производные при всех рациональных числах.

Смотрите также

• Диадическая трансформация
• Функция Вейерштрасса — функция, которая непрерывна всюду, но нигде не дифференцируема.

Примечания

1. Веструп 2003, Раздел 4.6.
2. Томсон, Брукнер и Брукнер 2008, стр. 252.
3. «Функция лестницы Кантора».
4. Басс 2013, стр. 28.
5. Дарст, Ричард (1993-09-01). "Размерность Хаусдорфа множества недифференцируемости функции Кантора равна [ln(2)/ln(3)]2". Труды Американского математического общества . 119 (1): 105–108. doi :10.2307/2159830. JSTOR  2159830.
6. Фальконер, Кеннет Дж. (2004-01-01). «Односторонний мультифрактальный анализ и точки недифференцируемости дьявольских лестниц». Математические труды Кембриджского философского общества . 136 (1): 167–174. Bibcode : 2004MPCPS.136..167F. doi : 10.1017/S0305004103006960 (неактивен 1 ноября 2024 г.). ISSN  1469-8064. S2CID  122381614.{{cite journal}}: CS1 maint: DOI inactive as of November 2024 (link)
7. Трошейт, Саша (2014-03-01). "Гёльдеровская дифференцируемость самоконформных дьявольских лестниц". Математические труды Кембриджского философского общества . 156 (2): 295–311. arXiv : 1301.1286 . Bibcode : 2014MPCPS.156..295T. doi : 10.1017/S0305004113000698. ISSN  1469-8064. S2CID  56402751.

Ссылки

• Басс, Ричард Франклин (2013) [2011]. Реальный анализ для аспирантов (Второе издание). Createspace Independent Publishing. ISBN 978-1-4818-6914-0.
• Кантор, Г. (1884). «De la puissance dessembles parfaits de point: Extrait d'une lettre adressée à l'éditeur» [Сила идеальных наборов точек: отрывок из письма, адресованного редактору]. Акта Математика . 4 . Международная пресса Бостона: 381–392. дои : 10.1007/bf02418423 . ISSN  0001-5962.Перепечатано в: Э. Цермело (ред.), Gesammelte Abhandlungen Mathematischen und Philosophischen Inhalts, Springer, Нью-Йорк, 1980.
• Дарст, Ричард Б.; Палагалло, Джудит А.; Прайс, Томас Э. (2010), Curious curves , Хакенсак, Нью-Джерси: World Scientific Publishing Co. Pte. Ltd., ISBN 978-981-4291-28-6, г-н  2681574
• Довгошей, О.; Мартио, О.; Рязанов В.; Вуоринен, М. (2006). «Функция Кантора». Экспозиции Mathematicae . 24 (1). Эльзевир Б.В.: 1–37. doi :10.1016/j.exmath.2005.05.002. ISSN  0723-0869. МР  2195181.
• Флерон, Джулиан Ф. (1994-04-01). «Заметка об истории множества Кантора и функции Кантора». Журнал «Математика» . 67 (2). Informa UK Limited: 136–140. doi : 10.2307/2690689. ISSN  0025-570X. JSTOR  2690689.
• Лебег, Х. (1904), Leçons sur l'intégration et la recherche des fonctions primes [ Уроки интегрирования и поиска примитивных функций ], Париж: Готье-Виллар
• Леони, Джованни (2017). Первый курс по пространствам Соболева. Том 181 (2-е изд.). Провиденс, Род-Айленд: Американское математическое общество. стр. 734. ISBN 978-1-4704-2921-8. OCLC  976406106.
• Шеффер, Людвиг (1884). «Allgemeine Untersuchungen über Rectification der Curven» [Общие исследования по исправлению кривых]. Акта Математика . 5 . Международная пресса Бостона: 49–82. дои : 10.1007/bf02421552 . ISSN  0001-5962.
• Томсон, Брайан С.; Брукнер, Джудит Б.; Брукнер, Эндрю М. (2008) [2001]. Элементарный вещественный анализ (Второе изд.). ClassicalRealAnalysis.com. ISBN 978-1-4348-4367-8.
• Веструп, Э. М. (2003). Теория мер и интегрирования . Ряды Уайли в теории вероятностей и статистике. John Wiley & sons. ISBN 978-0471249771.
• Витали, А. (1905), «Sulle funzioni Integrali» [Об целочисленных функциях], Atti Accad. наук. Турин Кл. наук. Фис. Мат. Природа. , 40 : 1021–1034

Внешние ссылки

• Троичная функция Кантора в Encyclopaedia of Mathematics
• Функция Кантора Дугласа Риверса, Демонстрационный проект Вольфрама .
• Вайсштейн, Эрик В. "Функция Кантора". MathWorld .