Подтверждая вытекающее

Тип ошибочного аргумента (логическая ошибка)

В пропозициональной логике утверждение следствия , иногда называемое ошибкой обратного утверждения , ошибкой обратного утверждения или путаницей необходимости и достаточности , является формальной ошибкой принятия истинного условного утверждения (например, «если бы лампа была разбита, то в комнате было бы темно») при определенных предположениях (в комнате нет других источников света, сейчас ночь и окна закрыты), и недействительным выводом его обратного («в комнате темно, поэтому лампа должна быть разбита»), даже если это утверждение может быть не истинным при тех же предположениях. Это возникает, когда следствие («в комнате было бы темно») имеет другие возможные антецеденты (например, «лампа находится в рабочем состоянии, но выключена» или «в комнате нет лампы»). ^[1]

Обратные ошибки распространены в повседневном мышлении и общении и могут быть результатом, среди прочего, проблем с общением, неправильных представлений о логике и неспособности учитывать другие причины. ^[2]

Противоположное утверждение, отрицающее следствие , называется modus tollens и является допустимой формой аргументации. ^[3]

Формальное описание

Существует четыре возможных формы смешанных гипотетических силлогизмов , две из которых являются действительными, а две — недействительными. Рассмотрение очень простого примера может помочь вам понять, почему эти формы являются действительными или недействительными. Если «p» представляет «Кандиру — рыба», а «q» представляет «Кандиру умеет плавать», попробуйте убедить себя, заменив эти утверждения на p и q в приведенной выше таблице. ^[4]

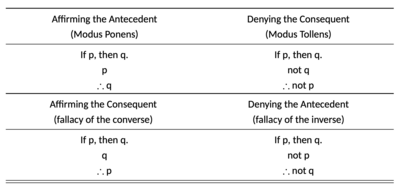
Утверждение консеквента — это действие, в ходе которого принимается истинное утверждение и делается недействительное заключение об обратном . Название «утверждение консеквента» происходит от использования консеквента Q для заключения антецедента P. Эту ошибку можно формально сформулировать как или, в качестве альтернативы, . ^[5] Коренной причиной такой логической ошибки иногда является неспособность понять, что просто потому, что P является возможным условием для Q , P может быть не единственным условием для Q , т. е. Q может следовать и из другого условия. ^{[6] [7]} ${\displaystyle P\to Q}$ ${\displaystyle Q\to P}$ ${\displaystyle P\to Q}$ ${\displaystyle (P\to Q,Q)\to P}$ ${\displaystyle {\frac {P\to Q,Q}{\therefore P}}}$

Утверждение следствия может также быть результатом чрезмерного обобщения опыта многих утверждений, имеющих истинные обратные. Если P и Q являются «эквивалентными» утверждениями, т. е . , то можно вывести P при условии Q . Например, утверждения «Сегодня 13 августа, поэтому у меня день рождения» и «Сегодня мой день рождения, поэтому у меня 13 августа» эквивалентны и оба являются истинными следствиями утверждения «13 августа — мой день рождения» (сокращенная форма ). ${\displaystyle P\leftrightarrow Q}$ ${\displaystyle P\to Q}$ ${\displaystyle Q\to P}$ ${\displaystyle P\leftrightarrow Q}$

Из возможных форм «смешанных гипотетических силлогизмов » две являются действительными, а две — недействительными. Утверждение антецедента ( modus ponens ) и отрицание консеквента ( modus tollens ) являются действительными. Утверждение консеквента и отрицание антецедента являются недействительными. ^[8]

Дополнительные примеры

Пример 1

Один из способов продемонстрировать несостоятельность этой формы аргумента — контрпример с истинными посылками, но очевидно ложным выводом. Например:

Если кто-то живет в Сан-Диего , значит, он живет в Калифорнии .

Джо живет в Калифорнии.

Следовательно, Джо живет в Сан-Диего.

В Калифорнии есть много мест, где можно жить, помимо Сан-Диего. С другой стороны, можно с уверенностью утверждать, что «если кто-то не живет в Калифорнии» ( не-Q ), то «этот человек не живет в Сан-Диего» ( не-P ). Это контрапозитив первого утверждения, и оно должно быть истинным, если и только если исходное утверждение истинно.

Пример 2

Если животное — собака, то у него четыре ноги.

У моего кота четыре ноги.

Следовательно, мой кот — собака.

Здесь сразу становится очевидным, что любое количество других антецедентов («Если животное — олень...», «Если животное — слон...», «Если животное — лось...» и т. д. ) может привести к следствию («тогда у него четыре ноги»), и что нелепо предполагать, что наличие четырех ног должно подразумевать, что животное — собака и ничего больше. Это полезно в качестве обучающего примера, поскольку большинство людей могут сразу понять, что достигнутый вывод должен быть неверным (интуитивно кошка не может быть собакой), и что метод, с помощью которого он был достигнут, должен быть ошибочным.

Пример 3

В Catch-22 [ ^9] капеллан допрашивается за то, что он якобы "Вашингтон Ирвинг"/"Ирвинг Вашингтон", который блокировал большие части писем солдат домой. Полковник нашел такое письмо, но с подписью капеллана.

«Но вы ведь умеете читать, не так ли?» — саркастически продолжал полковник. «Автор подписался».

«Там меня так зовут».

"Тогда ты это написал. QED "

В данном случае P — это «Капеллан подписывает свое имя», а Q — «Имя капеллана написано». Имя капеллана может быть написано, но он не обязательно его написал, как ложно заключает полковник. ^[9]

Смотрите также

• Абдуктивное рассуждение
• Апелляция к последствиям
• Путаница обратного
• Отрицание предшествующего
• Заблуждения о незаконном переносе
• Заблуждение о единственной причине
• Заблуждение нераспределенной середины
• Модус поненс
• Модус Толленс
• Необходимость и достаточность
• Post hoc ergo propter hoc

Ссылки

1. Розен, Кеннет Х. (2019). Дискретная математика и ее приложения: Кеннет Х. Розен . McGraw-Hill. ISBN 978-1260091991.
2. Лэй, Стивен (2014). Введение в анализ с доказательством, 5-е издание . Пирсон. ISBN 978-0321747471.
3. Херли, Патрик Дж. (2012). Краткое введение в логику (11-е изд.). Бостон, Массачусетс: Cengage Learning. стр. 362. ISBN 9781111346232. OCLC  711774631.
4. Кашеф, Арман (2023), В поисках универсальной логики: краткий обзор эволюции формальной логики, doi : 10.13140/RG.2.2.24043.82724/1
5. Херли, Патрик Дж. (2010), Краткое введение в логику (11-е издание). Wadsworth Cengage Learning, стр. 362–63.
6. "Утверждая следствие". Файлы заблуждений . Получено 9 мая 2013 г.
7. Дамер, Т. Эдвард (2001). «Спутывание необходимого с достаточным условием». Нападение на ошибочное рассуждение (4-е изд.). Уодсворт. стр. 150. ISBN 0-534-60516-8.
8. Келли, Дэвид (1998), Искусство рассуждения (3-е издание). Нортон, стр. 290–94.
9. Heller, Joseph (1994). Catch-22 . Винтаж. стр. 438, 8. ISBN 0-09-947731-9.