Сверхкороткий импульс

Лазерный импульс длительностью пикосекунда (10^-12 с) или меньше

В оптике сверхкороткий импульс , также известный как сверхбыстрое событие , представляет собой электромагнитный импульс , длительность которого составляет порядка пикосекунды (10−12 ^{секунды} ) или меньше. Такие импульсы имеют широкополосный оптический спектр и могут быть созданы генераторами с синхронизацией мод . Усиление сверхкоротких импульсов почти всегда требует техники усиления чирпированных импульсов , чтобы избежать повреждения усиливающей среды усилителя.

Они характеризуются высокой пиковой интенсивностью (или, правильнее сказать, облученностью ), что обычно приводит к нелинейным взаимодействиям в различных материалах, включая воздух. Эти процессы изучаются в области нелинейной оптики .

В специализированной литературе термин «ультракороткий» относится к фемтосекундному (фс) и пикосекундному (пс) диапазону, хотя такие импульсы больше не удерживают рекорд самых коротких импульсов, искусственно созданных. Действительно, сообщалось о рентгеновских импульсах с длительностью в аттосекундной шкале времени.

Нобелевская премия по химии 1999 года была присуждена Ахмеду Х. Зевайлу за использование сверхкоротких импульсов для наблюдения за химическими реакциями в масштабах времени, в которых они происходят, ^[1] открыв область фемтохимии . Еще одна Нобелевская премия, Нобелевская премия по физике 2023 года , также была присуждена за сверхкороткие импульсы. Эта премия была присуждена Пьеру Агостини , Ференцу Краусу и Анне Л'Юйе за разработку аттосекундных импульсов и их способность исследовать динамику электронов. ^[2]

Определение

Положительно чирпированный ультракороткий импульс света во временной области.

Стандартного определения ультракороткого импульса не существует. Обычно атрибут «ультракороткий» применяется к импульсам длительностью в несколько десятков фемтосекунд, но в более широком смысле любой импульс, который длится менее нескольких пикосекунд, можно считать ультракоротким. Различие между «ультракоротким» и «ультрабыстрым» необходимо, поскольку скорость, с которой распространяется импульс, является функцией показателя преломления среды, через которую он проходит, тогда как «ультракороткий» относится к временной ширине волнового пакета импульса . ^[3]

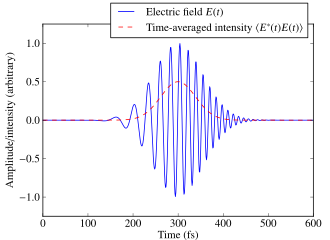
Типичным примером является чирпированный гауссов импульс, волна , амплитуда поля которой следует гауссовой огибающей , а мгновенная фаза имеет частотную развертку .

Фон

Реальное электрическое поле, соответствующее сверхкороткому импульсу, колеблется с угловой частотой ω _{0 ,} соответствующей центральной длине волны импульса. Для облегчения вычислений определяется комплексное поле E ( t ). Формально оно определяется как аналитический сигнал, соответствующий реальному полю.

Центральная угловая частота ω ₀ обычно явно записывается в комплексном поле, которое может быть разделено как временная функция интенсивности I ( t ) и временная фазовая функция ψ ( t ):

${\displaystyle E(t)={\sqrt {I(t)}}e^{i\omega _{0}t}e^{i\psi (t)}}$

Выражение комплексного электрического поля в частотной области получается из преобразования Фурье E ( t ):

${\displaystyle E(\omega )={\mathcal {F}}(E(t))}$

Из-за присутствия этого члена E ( ω ) центрируется вокруг ω ₀ , и общепринятой практикой является обозначение E ( ω - ω ₀ ) путем записи просто E ( ω ), что мы и будем делать в оставшейся части этой статьи. ${\displaystyle e^{i\omega _{0}t}}$

Так же, как и во временной области, интенсивность и фазовую функцию можно определить в частотной области:

${\displaystyle E(\omega )={\sqrt {S(\omega )}}e^{i\phi (\omega )}}$

Величина представляет собой спектральную плотность мощности (или просто спектр ) импульса, а представляет собой фазовую спектральную плотность (или просто спектральную фазу ). Примером спектральных фазовых функций является случай, когда является константой, в этом случае импульс называется импульсом с ограниченной полосой пропускания , или когда является квадратичной функцией, в этом случае импульс называется чирпированным импульсом из-за наличия мгновенной развертки частоты. Такой чирп может быть получен, когда импульс распространяется через материалы (например, стекло) и обусловлен их дисперсией . Это приводит к временному уширению импульса. ${\displaystyle S(\omega )}$ ${\displaystyle \phi (\omega )}$ ${\displaystyle \phi (\omega )}$ ${\displaystyle \phi (\omega )}$

Функции интенсивности — временная и спектральная — определяют длительность и ширину спектра импульса. Как утверждает принцип неопределенности , их произведение (иногда называемое произведением времени и ширины полосы) имеет нижнюю границу. Это минимальное значение зависит от определения, используемого для длительности, и от формы импульса. Для заданного спектра минимальное произведение времени и ширины полосы, а следовательно, и самый короткий импульс, получается с помощью импульса, ограниченного преобразованием, т. е. для постоянной спектральной фазы . Высокие значения произведения времени и ширины полосы, с другой стороны, указывают на более сложный импульс. ${\displaystyle I(t)}$ ${\displaystyle S(\omega )}$ ${\displaystyle \phi (\omega )}$

Управление формой импульса

Хотя оптические устройства, также используемые для непрерывного света, такие как расширители пучка и пространственные фильтры, могут использоваться для сверхкоротких импульсов, несколько оптических устройств были специально разработаны для сверхкоротких импульсов. Одним из них является компрессор импульсов ^[4] , устройство, которое может использоваться для управления спектральной фазой сверхкоротких импульсов. Он состоит из последовательности призм или решеток. При правильной настройке он может изменять спектральную фазу φ ( ω ) входного импульса так, что выходной импульс представляет собой импульс с ограниченной полосой пропускания и максимально короткой длительностью. Формирователь импульсов может использоваться для внесения более сложных изменений как в фазу, так и в амплитуду сверхкоротких импульсов.

Для точного управления импульсом необходима полная характеристика спектральной фазы импульса, чтобы получить определенную спектральную фазу импульса (например, ограниченную преобразованием ). Затем можно использовать пространственный модулятор света в плоскости 4f для управления импульсом. Многофотонное внутриимпульсное интерференционное фазовое сканирование (MIIPS) — это метод, основанный на этой концепции. С помощью фазового сканирования пространственного модулятора света MIIPS может не только характеризовать, но и манипулировать сверхкоротким импульсом, чтобы получить необходимую форму импульса в целевой точке (например, ограниченный преобразованием импульс для оптимизированной пиковой мощности и другие специфические формы импульса). Если формирователь импульса полностью откалиброван, этот метод позволяет контролировать спектральную фазу сверхкоротких импульсов с помощью простой оптической установки без движущихся частей. Однако точность MIIPS несколько ограничена по сравнению с другими методами, такими как оптическое стробирование с частотным разрешением (FROG). ^[5]

Методы измерения

Для измерения сверхкоротких оптических импульсов существует несколько методов.

Автокорреляция интенсивности определяет ширину импульса, если предполагается определенная форма импульса.

Спектральная интерферометрия (SI) — это линейный метод, который можно использовать, когда доступен предварительно охарактеризованный опорный импульс. Он дает интенсивность и фазу. Алгоритм, который извлекает интенсивность и фазу из сигнала SI, является прямым. Спектральная фазовая интерферометрия для прямой реконструкции электрического поля (SPIDER) — это нелинейный метод самореферирования, основанный на спектральной сдвиговой интерферометрии. Метод похож на SI, за исключением того, что опорный импульс является спектрально смещенной копией самого себя, что позволяет получить спектральную интенсивность и фазу зондирующего импульса с помощью процедуры прямой фильтрации FFT, аналогичной SI, но которая требует интеграции фазы, извлеченной из интерферограммы, для получения фазы зондирующего импульса.

Частотно-разрешенное оптическое стробирование (FROG) — это нелинейный метод, который позволяет получить интенсивность и фазу импульса. Это спектрально разрешенная автокорреляция. Алгоритм, который извлекает интенсивность и фазу из следа FROG, является итеративным. Решетчатое наблюдение сверхбыстрых падающих лазерных световых электронных полей ( GRENOUILLE ) — это упрощенная версия FROG. ( Grenouille по-французски означает « лягушка ».)

Chirp-сканирование — это метод, аналогичный MIIPS , который измеряет спектральную фазу импульса, применяя наклон квадратичных спектральных фаз и измеряя спектры второй гармоники. Что касается MIIPS, который требует много итераций для измерения спектральной фазы, для получения как амплитуды, так и фазы импульса требуется всего два chirp-сканирования. ^[6]

Многофотонное внутриимпульсное интерференционное фазовое сканирование (MIIPS) — это метод характеризации и управления сверхкороткими импульсами.

Распространение волновых пакетов в неизотропных средах

Частично повторяя вышеизложенное обсуждение, можно сказать, что приближение медленно меняющейся огибающей (SVEA) электрического поля волны с центральным волновым вектором и центральной частотой импульса определяется выражением: ${\displaystyle {\textbf {K}}_{0}}$ ${\displaystyle \omega _{0}}$

${\displaystyle {\textbf {E}}({\textbf {x}},t)={\textbf {A}}({\textbf {x}},t)\exp(i{\textbf {K}}_{0}{\textbf {x}}-i\omega _{0}t)}$

Мы рассматриваем распространение SVEA электрического поля в однородной дисперсионной неизотропной среде. Предполагая, что импульс распространяется в направлении оси z, можно показать, что огибающая для одного из наиболее общих случаев, а именно двуосного кристалла, управляется PDE : [ ^7] ${\displaystyle {\textbf {A}}}$

${\displaystyle {\frac {\partial {\textbf {A}}}{\partial z}}=~-~\beta _{1}{\frac {\partial {\textbf {A}}}{\partial t}}~-~{\frac {i}{2}}\beta _{2}{\frac {\partial ^{2}{\textbf {A}}}{\partial t^{2}}}~+~{\frac {1}{6}}\beta _{3}{\frac {\partial ^{3}{\textbf {A}}}{\partial t^{3}}}~+~\gamma _{x}{\frac {\partial {\textbf {A}}}{\partial x}}~+~\gamma _{y}{\frac {\partial {\textbf {A}}}{\partial y}}}$

${\displaystyle ~~~~~~~~~~~~+~i\gamma _{tx}{\frac {\partial ^{2}{\textbf {A}}}{\partial t\partial x}}~+~i\gamma _{ty}{\frac {\partial ^{2}{\textbf {A}}}{\partial t\partial y}}~-~{\frac {i}{2}}\gamma _{xx}{\frac {\partial ^{2}{\textbf {A}}}{\partial x^{2}}}~-~{\frac {i}{2}}\gamma _{yy}{\frac {\partial ^{2}{\textbf {A}}}{\partial y^{2}}}~+~i\gamma _{xy}{\frac {\partial ^{2}{\textbf {A}}}{\partial x\partial y}}+\cdots }$

где коэффициенты содержат эффекты дифракции и дисперсии, которые были определены аналитически с помощью компьютерной алгебры и проверены численно с точностью до третьего порядка как для изотропных, так и для неизотропных сред, действительных в ближнем и дальнем поле. — обратная величина проекции групповой скорости. Член в — дисперсия групповой скорости (GVD) или дисперсия второго порядка; он увеличивает длительность импульса и чирпит импульс по мере его распространения через среду. Член в — дисперсионный член третьего порядка, который может дополнительно увеличить длительность импульса, даже если обращается в нуль. Члены в и описывают снос импульса; коэффициент — это отношение компонента групповой скорости к единичному вектору в направлении распространения импульса (ось z). Члены в и описывают дифракцию оптического волнового пакета в направлениях, перпендикулярных оси распространения. Члены в и , содержащие смешанные производные по времени и пространству, вращают волновой пакет вокруг осей и , соответственно, увеличивают временную ширину волнового пакета (в дополнение к увеличению из-за GVD), увеличивают дисперсию в направлениях и , соответственно, и увеличивают чирп (в дополнение к тому, что из-за ), когда последний и/или и не обращаются в нуль. Член вращает волновой пакет в плоскости. Как ни странно, из-за ранее неполных расширений это вращение импульса не было реализовано до конца 1990-х годов, но оно было экспериментально подтверждено. ^[8] В третьем порядке обнаружено, что правая часть приведенного выше уравнения имеет следующие дополнительные члены для случая одноосного кристалла: ^[9] ${\displaystyle \beta _{1}}$ ${\displaystyle \beta _{2}}$ ${\displaystyle \beta _{3}}$ ${\displaystyle \beta _{2}}$ ${\displaystyle \gamma _{x}}$ ${\displaystyle \gamma _{y}}$ ${\displaystyle \gamma _{x}~(\gamma _{y})}$ ${\displaystyle x~(y)}$ ${\displaystyle \gamma _{xx}}$ ${\displaystyle \gamma _{yy}}$ ${\displaystyle \gamma _{tx}}$ ${\displaystyle \gamma _{ty}}$ ${\displaystyle y}$ ${\displaystyle x}$ ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle \beta _{2}}$ ${\displaystyle \gamma _{xx}}$ ${\displaystyle \gamma _{yy}}$ ${\displaystyle \gamma _{xy}}$ ${\displaystyle x-y}$

${\displaystyle \cdots ~+~{\frac {1}{3}}\gamma _{txx}{\frac {\partial ^{3}{\textbf {A}}}{\partial x^{2}\partial t}}~+~{\frac {1}{3}}\gamma _{tyy}{\frac {\partial ^{3}{\textbf {A}}}{\partial y^{2}\partial t}}~+~{\frac {1}{3}}\gamma _{ttx}{\frac {\partial ^{3}{\textbf {A}}}{\partial t^{2}\partial x}}+\cdots }$

Первый и второй члены отвечают за кривизну распространяющегося фронта импульса. Эти члены, включая член в , присутствуют в изотропной среде и учитывают сферическую поверхность распространяющегося фронта, исходящего из точечного источника. Член может быть выражен через показатель преломления, частоту и ее производные, и член также искажает импульс, но таким образом, что меняет роли и (см. ссылку на Trippenbach, Scott и Band для получения подробной информации). До сих пор трактовка здесь линейна, но нелинейные дисперсионные члены повсеместны в природе. Исследования, включающие дополнительный нелинейный член, показали, что такие члены оказывают глубокое влияние на волновой пакет, включая, среди прочего, самообострение волнового пакета. ^[10] Нелинейные аспекты в конечном итоге приводят к оптическим солитонам . ${\displaystyle \beta _{3}}$ ${\displaystyle \gamma _{txx}}$ ${\displaystyle \omega }$ ${\displaystyle \gamma _{ttx}}$ ${\displaystyle t}$ ${\displaystyle x}$ ${\displaystyle \gamma _{nl}|A|^{2}A}$

Несмотря на то, что SVEA довольно распространен, он не требуется для формулировки простого волнового уравнения, описывающего распространение оптических импульсов. Фактически, как показано в ^[11], даже очень общая форма электромагнитного волнового уравнения второго порядка может быть разложена на направленные компоненты, обеспечивая доступ к единому волновому уравнению первого порядка для самого поля, а не для огибающей. Для этого требуется только предположение, что эволюция поля медленная в масштабе длины волны и вообще не ограничивает полосу пропускания импульса, что наглядно продемонстрировано в [ ^{12] .}

Высокие гармоники

Высокоэнергетические сверхкороткие импульсы могут быть получены посредством генерации высоких гармоник в нелинейной среде . Высокоинтенсивный сверхкороткий импульс будет генерировать массив гармоник в среде; затем с помощью монохроматора выбирается конкретная интересующая гармоника . Эта техника использовалась для получения сверхкоротких импульсов в режимах экстремального ультрафиолета и мягкого рентгеновского излучения из импульсов лазера Ti-сапфир в ближнем инфракрасном диапазоне .

Приложения

Современная 3D-микро-/нанообработка материалов

Способность фемтосекундных лазеров эффективно изготавливать сложные структуры и устройства для широкого спектра применений была тщательно изучена в течение последнего десятилетия. Современные методы лазерной обработки с ультракороткими световыми импульсами могут быть использованы для структурирования материалов с субмикрометровым разрешением. Прямая лазерная запись (DLW) подходящих фоторезистов и других прозрачных сред может создавать сложные трехмерные фотонные кристаллы (PhC), микрооптические компоненты, решетки, каркасы тканевой инженерии (TE) и оптические волноводы. Такие структуры потенциально полезны для расширения возможностей приложений следующего поколения в телекоммуникациях и биоинженерии, которые полагаются на создание все более сложных миниатюрных деталей. Точность, скорость изготовления и универсальность сверхбыстрой лазерной обработки делают ее вполне подходящей для того, чтобы стать жизненно важным промышленным инструментом для производства. ^[13]

Микрообработка

Среди применений фемтосекундного лазера микротекстурирование поверхностей имплантатов было опробовано для улучшения формирования кости вокруг циркониевых зубных имплантатов. Метод продемонстрировал точность с очень низким термическим повреждением и уменьшением поверхностных загрязнений. Исследования на животных показали, что увеличение кислородного слоя и микро- и наночастиц, созданных микротекстурированием с помощью фемтосекундного лазера, привело к более высоким показателям формирования кости, более высокой плотности кости и улучшенной механической стабильности. ^{[14] [15] [16]}

Многофотонная полимеризация

Многофотонная полимеризация (MPP) выделяется своей способностью изготавливать микро- и наномасштабные структуры с исключительной точностью. Этот процесс использует концентрированную мощность фемтосекундных лазеров для инициирования высококонтролируемых реакций фотополимеризации, создавая подробные трехмерные конструкции. ^[17] Эти возможности делают MPP необходимым для создания сложных геометрий для биомедицинских приложений, включая тканевую инженерию и изготовление микроустройств, подчеркивая универсальность и точность сверхкоротких импульсных лазеров в передовых производственных процессах.

Смотрите также

• Аттосекундная хроноскопия
• Импульс с ограниченной полосой пропускания
• Фемтохимия
• Частотная гребенка
• Медицинская визуализация : сверхкороткие лазерные импульсы используются в многофотонных флуоресцентных микроскопах.
• Оптическая связь (ультракороткие импульсы). Фильтрация и формирование импульсов.
• Генерация и обнаружение терагерцового (Т-излучения) излучения.
• Сверхбыстрая лазерная спектроскопия
• Лазер сверхкоротких импульсов
• Волновой пакет

Ссылки

1. "Нобелевская премия по химии 1999 года". NobelPrize.org . Получено 18 октября 2023 г. .
2. "Нобелевская премия по физике 2023 года". NobelPrize.org . Получено 18 октября 2023 г. .
3. Пашотта, Рюдигер. «Энциклопедия лазерной физики и техники — сверхкороткие импульсы, фемтосекунды, лазеры». www.rp-photonics.com .
4. JC Diels, Фемтосекундные лазеры на красителях, в Dye Laser Principles , FJ Duarte и LW Hillman (ред.) (Academic, Нью-Йорк, 1990) Глава 3.
5. Комин, Альберто; Родес, Мишель; Цесельски, Ричард; Требино, Рик; Хартшу, Ахим (2015). «Характеристика импульсов в сверхбыстрой микроскопии: сравнение FROG, MIIPS и G-MIIPS». Cleo: 2015. стр. SW1H.5. doi :10.1364/CLEO_SI.2015.SW1H.5. ISBN 978-1-55752-968-8. S2CID  23655339.
6. Лорио, Винсент; Гитцингер, Грегори; Форже, Николас (2013). «Самостоятельная характеристика фемтосекундных лазерных импульсов с помощью сканирования с чирпом». Optics Express . 21 (21): 24879–93. Bibcode : 2013OExpr..2124879L. doi : 10.1364/OE.21.024879 . ISSN  1094-4087. PMID  24150331.
7. Band, YB; Trippenbach, Marek (1996). «Распространение оптических волновых пакетов в неизотропных средах». Physical Review Letters . 76 (9): 1457–1460. Bibcode : 1996PhRvL..76.1457B. doi : 10.1103/PhysRevLett.76.1457. PMID  10061728.
8. Radzewicz, C.; Krasinski, JS; La Grone, MJ; Trippenbach, M.; Band, YB (1997). "Интерферометрическое измерение наклона фемтосекундного волнового пакета в кристалле рутила". Журнал оптического общества Америки B. 14 ( 2): 420. Bibcode : 1997JOSAB..14..420R. doi : 10.1364/JOSAB.14.000420.
9. Trippenbach, Marek; Scott, TC; Band, YB (1997). «Распространение пучков и импульсов в ближнем и дальнем поле в дисперсионных средах» (PDF) . Optics Letters . 22 (9): 579–81. Bibcode :1997OptL...22..579T. doi :10.1364/OL.22.000579. PMID  18185596.
10. Trippenbach, Marek; Band, YB (1997). "Динамика расщепления коротких импульсов в дисперсионных нелинейных средах". Physical Review A. 56 ( 5): 4242–4253. Bibcode : 1997PhRvA..56.4242T. doi : 10.1103/PhysRevA.56.4242.
11. Кинслер, Пол (2010). «Распространение оптических импульсов с минимальными приближениями». Physical Review A. 81 ( 1): 013819. arXiv : 0810.5689 . Bibcode : 2010PhRvA..81a3819K. doi : 10.1103/PhysRevA.81.013819. ISSN  1050-2947.
12. Genty, G.; Kinsler, P.; Kibler, B.; Dudley, JM (2007). "Моделирование нелинейного уравнения огибающей динамики субцикла и генерации гармоник в нелинейных волноводах". Optics Express . 15 (9): 5382–7. Bibcode : 2007OExpr..15.5382G. doi : 10.1364/OE.15.005382 . ISSN  1094-4087. PMID  19532792.
13. Малинаускас, Мангирдас; Жукаускас, Альбертас; Хасэгава, Сатоши; Хаясаки, Ёсио; Мизейкис, Вигантас; Буйвидас, Ричардас; Юодказис, Саулюс (2016). «Сверхбыстрая лазерная обработка материалов: от науки к промышленности». Свет: наука и приложения . 5 (8): e16133. Бибкод : 2016LSA.....5E6133M. дои : 10.1038/lsa.2016.133. ISSN  2047-7538. ПМЦ 5987357 . ПМИД  30167182. 
14. Дельгадо-Руис, РА; Кальво-Гирадо, JL; Морено, П.; Гуардиа, Дж.; Гомес-Морено, Г.; Мате-Санчес, JE; Рамирес-Фернандес, П.; Чива, Ф. (2011). «Фемтосекундное лазерное микроструктурирование циркониевых дентальных имплантатов». Журнал исследований биомедицинских материалов. Часть B: Прикладные биоматериалы . 96Б (1): 91–100. дои : 10.1002/jbm.b.31743. ISSN  1552-4973. ПМИД  21061361.
15. Кальво Гирадо и др., 2013 и 2014 гг.
16. Дельгадо-Руис и др., 2014)
17. "Многофотонная полимеризация". www.litilit.com . Получено 2024-04-02 .

Дальнейшее чтение

• Hirlimann, C. (2004). "Импульсная оптика". В Rullière, Claude (ред.). Femtosecond Laser Pulses: Principles and Experiments (2-е изд.). New York: Springer. ISBN 0-387-01769-0.
• Эндрю М. Вайнер (2009). Ultrafast Optics. Хобокен, Нью-Джерси: Wiley. ISBN 978-0-471-41539-8.
• JC Diels и W. Rudolph (2006). Явления сверхкоротких лазерных импульсов . Нью-Йорк, Academic. ISBN 978-0-12-215493-5.

Внешние ссылки

• Виртуальная фемтосекундная лаборатория Lab2
• Анимация распространения коротких импульсов в случайной среде (YouTube)
• Сверхбыстрые лазеры: анимированное руководство по работе лазеров и усилителей на основе титан-сапфира.