Теорема Кондорсе о жюри

Теорема политологии

График кумулятивных вероятностей успеха (ось Y) для нескольких биномиальных распределений с заданными индивидуальными шансами на успех (ось X) и числом «присяжных» (цвет).

Теорема присяжных Кондорсе — это теорема политической науки об относительной вероятности принятия данной группой лиц правильного решения. Теорема была впервые высказана маркизом де Кондорсе в его работе 1785 года «Опыт о применении анализа к вероятности решений большинства» . ^[1]

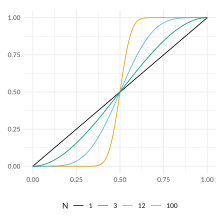
Предположения теоремы таковы, что группа желает принять решение большинством голосов . Один из двух результатов голосования является правильным , и каждый избиратель имеет независимую вероятность p проголосовать за правильное решение. Теорема спрашивает, сколько избирателей мы должны включить в группу. Результат зависит от того, больше или меньше p 1/2:

• Если p больше 1/2 (каждый избиратель с большей вероятностью проголосует правильно), то добавление большего количества избирателей увеличивает вероятность того, что решение большинства будет правильным. В пределе вероятность того, что большинство проголосует правильно, приближается к 1 по мере увеличения числа избирателей.
• С другой стороны, если p меньше 1/2 (каждый избиратель с большей вероятностью проголосует неправильно), то добавление большего количества избирателей ухудшает ситуацию: оптимальное жюри состоит из одного избирателя.

После Кондорсе многие другие исследователи доказали различные другие теоремы присяжных , ослабив некоторые или все предположения Кондорсе.

Доказательства

Доказательство 1: Расчет вероятности того, что два дополнительных избирателя изменят результат

Чтобы избежать необходимости в правиле разрешения ничьей, мы предполагаем, что n нечетное. По сути, тот же аргумент работает для четного n , если ничья разрешается добавлением одного избирателя.

Теперь предположим, что мы начинаем с n избирателей, и пусть m из этих избирателей проголосуют правильно.

Рассмотрим, что произойдет, если мы добавим еще двух избирателей (чтобы общее число оставалось нечетным). Большинство голосов изменится только в двух случаях:

• m было на один голос меньше, чем нужно, чтобы получить большинство из n голосов, но оба новых избирателя проголосовали правильно.
• m как раз равнялось большинству из n голосов, но оба новых избирателя проголосовали неправильно.

В остальное время новые голоса либо отменяют, либо только увеличивают разрыв, либо не оказывают существенного влияния. Поэтому нас волнует только то, что происходит, когда один голос (среди первых n ) отделяет правильное большинство от неправильного.

Ограничивая наше внимание этим случаем, мы можем представить, что первые n -1 голосов аннулируются и что решающий голос отдается n -ным избирателем. В этом случае вероятность получения правильного большинства равна просто p . Теперь предположим, что мы отправляем двух дополнительных избирателей. Вероятность того, что они изменят неправильное большинство на правильное, равна (1- p ) p ² , в то время как вероятность того, что они изменят правильное большинство на неправильное, равна p (1- p ) ² . Первая из этих вероятностей больше второй тогда и только тогда, когда p > 1/2, что доказывает теорему.

Доказательство 2: Расчет вероятности того, что решение верно

Это доказательство прямое; оно просто суммирует вероятности большинства. Каждый член суммы умножает количество комбинаций большинства на вероятность этого большинства. Каждое большинство подсчитывается с использованием комбинации , n элементов, взятых по k за раз, где n — размер жюри, а k — размер большинства. Вероятности варьируются от 0 (= голос всегда неправильный) до 1 (= всегда правильный). Каждый человек принимает решение независимо, поэтому вероятности их решений перемножаются. Вероятность каждого правильного решения равна p . Вероятность неправильного решения, q , противоположна p , то есть 1 − p . Запись мощности, ie, является сокращением для x умножений p . ${\displaystyle p^{x}}$

Точность решений комитета или жюри можно легко оценить, используя этот подход в компьютерных таблицах или программах.

В качестве примера возьмем простейший случай n = 3, p = 0,8. Нам нужно показать, что 3 человека имеют шанс быть правыми выше 0,8. Действительно:

0,8×0,8×0,8 + 0,8×0,8×0,2 + 0,8×0,2×0,8 + 0,2×0,8×0,8 = 0,896.

Асимптотика

Асимптотика — это «исчисление приближений». Оно используется для решения сложных задач, которые не могут быть решены точно, и для предоставления более простых форм сложных результатов, от ранних результатов, таких как формулы Тейлора и Стирлинга, до теоремы о простых числах. Важной темой в изучении асимптотики является асимптотическое распределение, которое является распределением вероятностей, которое в некотором смысле является «предельным» распределением последовательности распределений. Вероятность правильного решения большинства P ( n ,  p ), когда индивидуальная вероятность p близка к 1/2, растет линейно в терминах p − 1/2. Для n избирателей, каждый из которых имеет вероятность p принять правильное решение, и для нечетного n (где нет возможных ничьих):

${\displaystyle P(n,p)=1/2+c_{1}(p-1/2)+c_{3}(p-1/2)^{3}+O\left((p-1/2)^{5}\right),}$

где

${\displaystyle c_{1}={n \choose {\lfloor n/2\rfloor }}{\frac {\lfloor n/2\rfloor +1}{4^{\lfloor n/2\rfloor }}}={\sqrt {\frac {2n+1}{\pi }}}\left(1+{\frac {1}{16n^{2}}}+O(n^{-3})\right),}$

и асимптотическое приближение в терминах n очень точное. Разложение происходит только в нечетных степенях и . Проще говоря, это означает, что когда решение трудное ( p близко к 1/2), выигрыш от наличия n избирателей растет пропорционально . ^[2] ${\displaystyle c_{3}<0}$ ${\displaystyle {\sqrt {n}}}$

Теорема в других дисциплинах

Теорема жюри Кондорсе недавно использовалась для концептуализации интеграции оценок, когда несколько врачей-читателей (рентгенологов, эндоскопистов и т. д.) независимо оценивают изображения на предмет активности заболевания. Эта задача возникает при центральном считывании, выполняемом во время клинических испытаний, и имеет сходство с голосованием. По мнению авторов, применение теоремы может перевести индивидуальные оценки читателей в окончательную оценку способом, который является как математически обоснованным (избегая усреднения порядковых данных), так и математически поддающимся дальнейшему анализу, и способом, который соответствует текущей задаче оценки (основанной на решениях о наличии или отсутствии признаков, субъективная задача классификации) ^[3].

Теорема жюри Кондорсе также используется в ансамблевом обучении в области машинного обучения . ^[4] Ансамблевой метод объединяет предсказания многих отдельных классификаторов путем голосования большинства. Предполагая, что каждый из отдельных классификаторов предсказывает с точностью чуть больше 50% и их предсказания независимы, тогда ансамбль их предсказаний будет намного больше, чем их индивидуальные предсказательные оценки.

Применимость к демократическим процессам

Многие политические теоретики и философы используют теорему Кондорсе о жюри (CJT) для защиты демократии, см. Бреннан ^[5] и ссылки в ней. Тем не менее, это эмпирический вопрос, выполняется ли теорема в реальной жизни или нет. Обратите внимание, что CJT — это палка о двух концах : она может либо доказать, что правило большинства является (почти) идеальным механизмом для агрегации информации, когда , либо (почти) идеальной катастрофой, когда . Катастрофа будет означать, что систематически выбирается неправильный вариант. Некоторые авторы утверждают, что мы находимся в последнем сценарии. Например, Брайан Каплан подробно доказывал , что знания избирателей систематически смещены в сторону (вероятно) неправильных вариантов. В установке CJT это можно было бы интерпретировать как доказательство . ${\displaystyle p>1/2}$ ${\displaystyle p<1/2}$ ${\displaystyle p<1/2}$

Недавно был принят другой подход к изучению применимости CJT. ^[6] Вместо рассмотрения однородного случая каждому избирателю разрешается иметь вероятность , возможно, отличную от других избирателей. Этот случай ранее изучали Дэниел Беренд и Джейкоб Пароуш ^[7] и включает классическую теорему Кондорсе (когда ) и другие результаты, такие как Чудо агрегации (когда для большинства избирателей и для небольшой их части). Затем, следуя байесовскому подходу, оценивается априорная вероятность (в данном случае априори ) тезиса, предсказанного теоремой. То есть, если мы выберем произвольную последовательность избирателей (т. е. последовательность ), будет ли тезис CJT верен? Ответ — нет. Точнее, если случайная последовательность берется после несмещенного распределения, которое не благоприятствует компетентности, , или некомпетентности, , то тезис, предсказанный теоремой, не будет верен почти наверняка . С этим новым подходом сторонники CJT должны представить веские доказательства компетентности, чтобы преодолеть низкую априорную вероятность. То есть, дело не только в том, что есть доказательства против компетентности (апостериорная вероятность), но и в том, что мы не можем ожидать, что CJT будет работать при отсутствии каких-либо доказательств (априорная вероятность). ${\displaystyle p_{i}\in [0,1]}$ ${\displaystyle p_{i}=p~~\forall ~i\in \mathbb {N} }$ ${\displaystyle p_{i}=1/2}$ ${\displaystyle p_{i}=1}$ ${\displaystyle (p_{i})_{i\in \mathbb {N} }}$ ${\displaystyle p_{i}}$ ${\displaystyle p_{i}>1/2}$ ${\displaystyle p_{i}<1/2}$

Дальнейшее чтение

• Метод Кондорсе
• Парадокс Кондорсе
• Теорема присяжных
• Закон больших чисел
• Мудрость толпы

Примечания

1. Маркиз де Кондорсе (1785). Essai sur l'application de l'analyse à la probilité des decisions rendues à la множественности голосов (PNG) (на французском языке) . Проверено 10 марта 2008 г.
2. Макленнан, Эндрю (1998). «Последствия теоремы Кондорсе о жюри для выгодного агрегирования информации рациональными агентами». The American Political Science Review . 92 (2): 413–418. doi :10.2307/2585673. ISSN  0003-0554. JSTOR  2585673.
3. Готтлиб, Клаус; Хуссейн, Фес (2015-02-19). «Голосование за оценку и подсчет изображений (VISA) — теория и применение алгоритма считывания 2 + 1 для повышения точности конечных точек визуализации в клинических испытаниях». BMC Medical Imaging . 15 : 6. doi : 10.1186/s12880-015-0049-0 . ISSN  1471-2342. PMC 4349725 . PMID  25880066. 
4. "Случайный лес". mlu-explain.github.io . Получено 2022-05-24 .
5. Бреннан, Джейсон (2011). «Теорема Кондорсе о жюри и оптимальное число избирателей». Политика . 31 (2): 55–62. doi :10.1111/j.1467-9256.2011.01403.x. ISSN  0263-3957. S2CID  152938266.
6. Романьега Санчо, Альваро (2022). «О вероятности теоремы Кондорсе о Жюри или о чуде агрегации». Математические общественные науки . 119 : 41–55. arXiv : 2108.00733 . doi :10.1016/j.mathsocsci.2022.06.002. S2CID  249921504.
7. Беренд, Дэниел; Паруш, Джейкоб (1998). «Когда теорема Кондорсе о жюри верна?». Социальный выбор и благосостояние . 15 (4): 481–488. doi :10.1007/s003550050118. ISSN  0176-1714. JSTOR  41106274. S2CID  120012958.