Теория солнечных элементов

Теория солнечных элементов объясняет процесс, посредством которого энергия света в фотонах преобразуется в электрический ток, когда фотоны попадают в подходящий полупроводниковый прибор . Теоретические исследования имеют практическое применение, поскольку они предсказывают фундаментальные ограничения солнечного элемента и дают указания относительно явлений, которые способствуют потерям и эффективности солнечного элемента .

Зонная диаграмма солнечного элемента, соответствующая очень низкому току (горизонтальный уровень Ферми ), очень низкому напряжению (валентные зоны металла на одной высоте) и, следовательно, очень низкой освещенности

Рабочее объяснение

1. Фотоны солнечного света попадают на солнечную панель и поглощаются полупроводниковыми материалами.
2. Электроны (отрицательно заряженные) выбиваются из своих атомов, когда они возбуждаются. Из-за их особой структуры и материалов в солнечных элементах, электронам разрешено двигаться только в одном направлении. Электронная структура материалов очень важна для работы процесса, и часто кремний, включающий небольшие количества бора или фосфора, используется в разных слоях.
3. Массив солнечных элементов преобразует солнечную энергию в полезное количество электроэнергии постоянного тока .

Фотогенерация носителей заряда

Когда фотон попадает в полупроводник, может произойти одно из трех:

1. Фотон может проходить напрямую через полупроводник — это (обычно) происходит с фотонами с более низкой энергией.
2. Фотон может отражаться от поверхности.
3. Фотон может быть поглощен полупроводником, если энергия фотона превышает ширину запрещенной зоны . Это приводит к образованию пары электрон-дырка и иногда к выделению тепла в зависимости от структуры зоны.

Зонная диаграмма кремниевого солнечного элемента, соответствующая очень низкому току (горизонтальный уровень Ферми ), очень низкому напряжению (валентные зоны металла на одной высоте) и, следовательно, очень низкой освещенности.

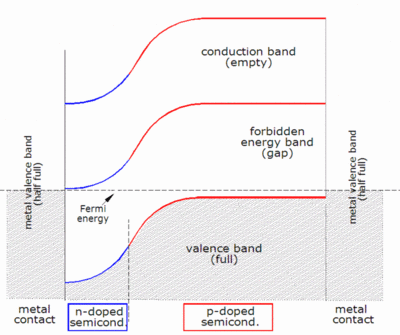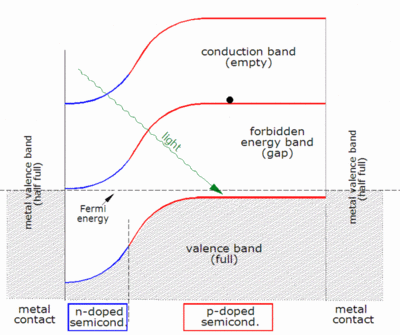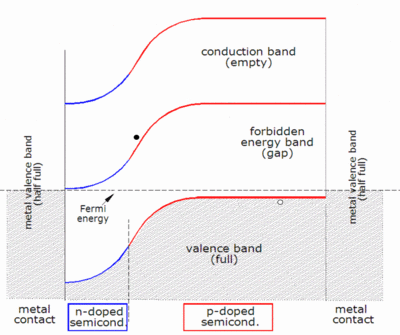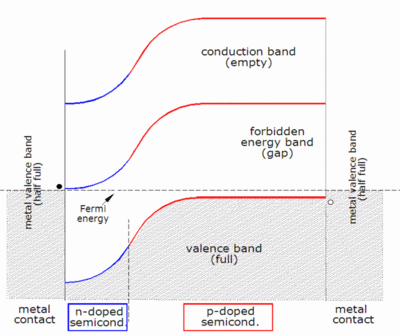
Когда фотон поглощается, его энергия передается электрону в кристаллической решетке. Обычно этот электрон находится в валентной зоне . Энергия, переданная электрону фотоном, «возбуждает» его в зону проводимости , где он может свободно перемещаться внутри полупроводника. Сеть ковалентных связей, частью которой ранее был электрон, теперь имеет на один электрон меньше. Это известно как дырка, и она имеет положительный заряд. Наличие отсутствующей ковалентной связи позволяет связанным электронам соседних атомов перемещаться в «дырку», оставляя позади другую дырку, таким образом распространяя дырки по всей решетке в направлении, противоположном движению отрицательно заряженных электронов. Можно сказать, что фотоны, поглощенные в полупроводнике, создают пары электрон-дырка.

Фотону достаточно иметь энергию, превышающую ширину запрещенной зоны, чтобы возбудить электрон из валентной зоны в зону проводимости. Однако спектр солнечных частот приближается к спектру черного тела при температуре около 5800 К, ^[1] и, таким образом, большая часть солнечного излучения, достигающего Земли, состоит из фотонов с энергией, превышающей ширину запрещенной зоны кремния (1,12 эВ), что близко к идеальному значению для земного солнечного элемента (1,4 эВ). Эти фотоны с более высокой энергией будут поглощаться кремниевым солнечным элементом, но разница в энергии между этими фотонами и шириной запрещенной зоны кремния преобразуется в тепло (через колебания решетки — называемые фононами ), а не в полезную электрическую энергию.

P–n-переход

Наиболее известный солнечный элемент сконфигурирован как p–n-переход большой площади , изготовленный из кремния. В качестве упрощения можно представить себе приведение слоя кремния n-типа в прямой контакт со слоем кремния p-типа. Легирование n-типа производит подвижные электроны (оставляя положительно заряженные доноры), в то время как легирование p-типа производит подвижные дырки (и отрицательно заряженные акцепторы). На практике p–n-переходы кремниевых солнечных элементов изготавливаются не таким образом, а путем диффузии легирующей примеси n-типа в одну сторону пластины p-типа (или наоборот).

Если кусок кремния p-типа поместить в тесный контакт с куском кремния n-типа, то произойдет диффузия электронов из области высокой концентрации электронов (сторона n-типа перехода) в область низкой концентрации электронов (сторона p-типа перехода). Когда электроны диффундируют в сторону p-типа, каждый из них уничтожает дырку, делая эту сторону отрицательно заряженной (потому что теперь количество подвижных положительных дырок теперь меньше количества отрицательных акцепторов). Аналогично, дырки, диффундирующие в сторону n-типа, делают ее более положительно заряженной. Однако (при отсутствии внешней цепи) этот диффузионный ток носителей не продолжается бесконечно, потому что накопление заряда по обе стороны перехода создает электрическое поле , которое препятствует дальнейшей диффузии большего количества зарядов. В конце концов, достигается равновесие, при котором чистый ток равен нулю, оставляя область по обе стороны перехода, где электроны и дырки диффундировали через переход и уничтожили друг друга, называемую областью обеднения, потому что она практически не содержит подвижных носителей заряда. Ее также называют областью пространственного заряда , хотя пространственный заряд распространяется немного дальше в обоих направлениях, чем область обеднения.

После установления равновесия пары электронов и дырок, образующиеся в обедненной области, разделяются электрическим полем, при этом электрон притягивается к положительной стороне n-типа, а дырки — к отрицательной стороне p-типа, что уменьшает заряд (и электрическое поле), созданный только что описанной диффузией. Если устройство не подключено (или внешняя нагрузка очень велика), то диффузионный ток в конечном итоге восстановит равновесный заряд, перенеся электрон и дырку обратно через соединение, но если подключенная нагрузка достаточно мала, электроны предпочитают двигаться по внешней цепи в попытке восстановить равновесие, выполняя полезную работу по пути.

Разделение носителей заряда

Существуют две причины движения и разделения носителей заряда в солнечном элементе:

1. дрейф носителей, вызванный электрическим полем, при котором электроны выталкиваются в одну сторону, а дырки — в другую
2. диффузия носителей из зон с более высокой концентрацией носителей в зоны с более низкой концентрацией носителей (вследствие градиента химического потенциала).

Эти две «силы» могут работать друг против друга в любой заданной точке ячейки. Например, электрон, движущийся через соединение из p-области в n-область (как на схеме в начале этой статьи), подталкивается электрическим полем против градиента концентрации. То же самое касается дырки, движущейся в противоположном направлении.

Проще всего понять, как генерируется ток, если рассматривать пары электрон-дырка, которые создаются в обедненной зоне, где есть сильное электрическое поле. Электрон подталкивается этим полем к стороне n, а дырка — к стороне p. (Это противоположно направлению тока в прямосмещенном диоде, таком как работающий светодиод .) Когда пара создается вне зоны пространственного заряда, где электрическое поле меньше, диффузия также действует на перемещение носителей, но соединение все еще играет роль, выметая любые электроны, которые достигают его, со стороны p на сторону n и выметая любые дырки, которые достигают его, со стороны n на сторону p, тем самым создавая градиент концентрации вне зоны пространственного заряда.

В толстых солнечных элементах очень мало электрического поля в активной области за пределами зоны пространственного заряда, поэтому доминирующим режимом разделения носителей заряда является диффузия. В этих элементах длина диффузии неосновных носителей (длина, которую могут пройти фотогенерированные носители до того, как они рекомбинируют) должна быть большой по сравнению с толщиной элемента. В тонкопленочных элементах (таких как аморфный кремний) длина диффузии неосновных носителей обычно очень коротка из-за наличия дефектов, и поэтому доминирующим разделением заряда является дрейф, обусловленный электростатическим полем перехода, который распространяется на всю толщину элемента. ^[2]

Как только неосновной носитель попадает в область дрейфа, он «проносится» через переход и, на другой стороне перехода, становится основным носителем. Этот обратный ток является током генерации, питаемым как термически, так и (если присутствует) поглощением света. С другой стороны, основные носители перемещаются в область дрейфа посредством диффузии (в результате градиента концентрации), что приводит к прямому току; только основные носители с самыми высокими энергиями (в так называемом хвосте Больцмана; ср. статистику Максвелла–Больцмана ) могут полностью пересечь область дрейфа. Следовательно, распределение носителей во всем устройстве регулируется динамическим равновесием между обратным током и прямым током.

Подключение к внешней нагрузке

Омические контакты металл -полупроводник выполнены как на стороне n-типа, так и на стороне p-типа солнечного элемента, а электроды подключены к внешней нагрузке. Электроны, которые созданы на стороне n-типа или созданы на стороне p-типа, «собранные» переходом и перенесенные на сторону n-типа, могут перемещаться по проводу, питать нагрузку и продолжать движение по проводу, пока не достигнут контакта полупроводник-металл p-типа. Здесь они рекомбинируют с дыркой, которая была либо создана как пара электрон-дырка на стороне p-типа солнечного элемента, либо с дыркой, которая была перенесена через переход со стороны n-типа после того, как была создана там.

Измеренное напряжение равно разнице квазиуровней Ферми основных носителей заряда (электронов в n-части и дырок в p-части) на двух клеммах. ^[3]

Эквивалентная схема солнечного элемента

Эквивалентная схема солнечного элемента

Эквивалентная схема модели p–n-перехода идеального солнечного элемента использует идеальный источник тока (фотогенерированный ток которого увеличивается с интенсивностью света) параллельно с диодом (ток которого представляет собой рекомбинационные потери). Для учета резистивных потерь шунтирующее сопротивление и последовательное сопротивление добавляются как сосредоточенные элементы . ^[4] Результирующий выходной ток равен фотогенерированному току за вычетом токов через диод и шунтирующий резистор: ^{[5] [6]} ${\displaystyle I_{\text{L}}}$ ${\displaystyle I_{\text{D}}}$ ${\displaystyle R_{\text{SH}}}$ ${\displaystyle R_{\text{S}}}$ ${\displaystyle I_{\text{out}}}$

${\displaystyle I_{\text{out}}=I_{\text{L}}-I_{\text{D}}-I_{\text{SH}}}$

Напряжение перехода (как на диоде, так и на сопротивлении шунта) равно:

${\displaystyle V_{\text{j}}=V_{\text{out}}+I_{\text{out}}\,R_{\text{S}}}$

где - напряжение на выходных клеммах. Ток утечки через шунтирующий резистор пропорционален напряжению перехода , согласно закону Ома : ${\displaystyle V_{\text{out}}}$ ${\displaystyle I_{\text{SH}}}$ ${\displaystyle V_{\text{j}}}$

${\displaystyle I_{\text{SH}}={\frac {V_{\text{j}}}{R_{\text{SH}}}}}$

По уравнению диода Шокли ток, проходящий через диод, равен:

${\displaystyle I_{\text{D}}=I_{0}\left\{\exp \left[{\frac {V_{\text{j}}}{nV_{\text{T}}}}\right]-1\right\}}$^[7]

где

• I ₀ , обратный ток насыщения
• n , коэффициент идеальности диода (1 для идеального диода)
• q , элементарный заряд
• k , постоянная Больцмана
• T , абсолютная температура
• ${\displaystyle V_{\text{T}}=kT/q,}$тепловое напряжение . При 25 °C, вольт. ${\displaystyle V_{\text{T}}\approx 0.0259}$

Подставляя их в первое уравнение, получаем характеристическое уравнение солнечного элемента, которое связывает параметры солнечного элемента с выходным током и напряжением:

${\displaystyle I_{\text{out}}=I_{\text{L}}-I_{0}\left\{\exp \left[{\frac {V_{\text{out}}+I_{\text{out}}R_{\text{S}}}{nV_{\text{T}}}}\right]-1\right\}-{\frac {V_{\text{out}}+I_{\text{out}}R_{\text{S}}}{R_{\text{SH}}}}.}$

Альтернативный вывод дает уравнение, похожее по виду, но с левой стороны. Две альтернативы являются тождествами ; то есть они дают совершенно одинаковые результаты. ${\displaystyle V_{\text{out}}}$

Поскольку параметры I ₀ , n , RS и R _SH невозможно измерить напрямую, наиболее распространенным применением характеристического уравнения является нелинейная регрессия _для извлечения значений этих параметров на основе их совместного влияния на поведение солнечного элемента.

Если R _S не равно нулю, то приведенное выше уравнение не дает прямого результата, но его можно решить с помощью функции Ламберта W : ${\displaystyle I_{\text{out}}}$

${\displaystyle I_{\text{out}}={\frac {(I_{\text{L}}+I_{0})-V_{\text{out}}/R_{\text{SH}}}{1+R_{\text{S}}/R_{\text{SH}}}}-{\frac {nV_{\text{T}}}{R_{\text{S}}}}W\left({\frac {I_{0}R_{\text{S}}}{nV_{\text{T}}(1+R_{\text{S}}/R_{\text{SH}})}}\exp \left({\frac {V_{\text{out}}}{nV_{\text{T}}}}\left(1-{\frac {R_{\text{S}}}{R_{\text{S}}+R_{\text{SH}}}}\right)+{\frac {(I_{\text{L}}+I_{0})R_{\text{S}}}{nV_{\text{T}}(1+R_{\text{S}}/R_{\text{SH}})}}\right)\right)}$

При использовании внешней нагрузки с ячейкой ее сопротивление можно просто прибавить к R _S и установить равным нулю, чтобы найти ток. ${\displaystyle V_{\text{out}}}$

Когда мало, мы можем использовать приближение как для получения чего-то, с чем гораздо проще работать ${\displaystyle I_{0}R_{\text{S}}/nV_{\text{T}}}$ ${\displaystyle x^{-1}W\left(xy\right)\to y}$ ${\displaystyle x\to 0}$

${\displaystyle I_{\text{out}}={\frac {(I_{\text{L}}+I_{0})-V_{\text{out}}/R_{\text{SH}}}{1+R_{\text{S}}/R_{\text{SH}}}}-{\frac {I_{0}}{(1+R_{\text{S}}/R_{\text{SH}})}}\exp \left({\frac {V_{\text{out}}}{nV_{\text{T}}}}\left(1-{\frac {R_{\text{S}}}{R_{\text{S}}+R_{\text{SH}}}}\right)+{\frac {(I_{\text{L}}+I_{0})R_{\text{S}}}{nV_{\text{T}}(1+R_{\text{S}}/R_{\text{SH}})}}\right).}$

Теперь возможны еще несколько упрощений, например, когда что приводит к ${\displaystyle R_{\text{S}}\ll R_{\text{SH}}}$

${\displaystyle I_{\text{out}}=I_{\text{L}}+I_{0}-{\frac {V_{\text{out}}}{R_{\text{SH}}}}-I_{0}\exp \left({\frac {V_{\text{out}}+(I_{\text{L}}+I_{0})R_{\text{S}}}{nV_{\text{T}}}}\right).}$

Когда ток, генерируемый фотоэлектрическим модулем, велик по сравнению с током в шунте, т.е. (потому что сопротивление шунта велико), существует аналитическое решение для для любого меньшего, чем : ${\displaystyle I_{\text{L}}\gg V_{\text{out}}/R_{\text{SH}}}$ ${\displaystyle V_{\text{out}}}$ ${\displaystyle I_{\text{out}}}$ ${\displaystyle I_{\text{L}}+I_{0}}$

${\displaystyle V_{\text{out}}=nV_{\text{T}}\ln \left({\frac {I_{\text{L}}-I_{\text{out}}}{I_{0}}}+1\right)-(I_{\text{L}}+I_{0})R_{\text{S}}.}$

В противном случае можно решить задачу с помощью функции Ламберта W: ${\displaystyle V_{\text{out}}}$

${\displaystyle V=(I_{\text{L}}+I_{0})R_{\text{SH}}-I(R_{\text{S}}+R_{\text{SH}})-nV_{\text{T}}W\left({\frac {I_{0}R_{\text{SH}}}{nV_{\text{T}}}}\exp \left({\frac {(I_{\text{L}}+I_{0}-I)R_{\text{SH}}}{nV_{\text{T}}}}\right)\right)}$

Однако, когда R _SH велико, исходное уравнение лучше решить численно.

Общая форма решения представляет собой кривую с уменьшением по мере увеличения (см. графики ниже). Наклон при малых или отрицательных (где функция W близка к нулю) приближается к , тогда как наклон при больших приближается к . Поэтому для высокой оптимальной выходной мощности желательно иметь большой и должен быть маленьким. ${\displaystyle I_{\text{out}}}$ ${\displaystyle V_{\text{out}}}$ ${\displaystyle V_{\text{out}}}$ ${\displaystyle -1/(R_{\text{S}}+R_{\text{SH}})}$ ${\displaystyle V_{\text{out}}}$ ${\displaystyle -1/R_{\text{S}}}$ ${\displaystyle P_{\text{out}}=I_{\text{out}}V_{\text{out}}}$ ${\displaystyle R_{\text{SH}}}$ ${\displaystyle R_{\text{S}}}$

Напряжение холостого хода и ток короткого замыкания

Когда ячейка работает в режиме разомкнутой цепи , = 0 и напряжение на выходных клеммах определяется как напряжение разомкнутой цепи . Предполагая, что сопротивление шунта достаточно велико, чтобы пренебречь последним членом характеристического уравнения, напряжение разомкнутой цепи V _OC равно: ${\displaystyle I_{\text{out}}}$

${\displaystyle V_{\text{OC}}\approx {\frac {nkT}{q}}\ln \left({\frac {I_{\text{L}}}{I_{0}}}+1\right).}$

Аналогично, когда ячейка работает при коротком замыкании , = 0 и ток через клеммы определяется как ток короткого замыкания . Можно показать, что для высококачественной солнечной ячейки (низкие R _S и I ₀ , и высокий R _SH ) ток короткого замыкания равен: ${\displaystyle V_{\text{out}}}$ ${\displaystyle I_{\text{SC}}}$

${\displaystyle I_{\text{SC}}\approx I_{\text{L}}.}$

Извлечение энергии из устройства невозможно при работе в условиях как разомкнутой цепи, так и короткого замыкания.

Влияние физического размера

Значения I _L , I ₀ , R _S и R _SH зависят от физического размера солнечного элемента. При сравнении в остальном идентичных элементов, элемент с площадью перехода в два раза больше другого, в принципе, будет иметь в два раза больше I _L и I _{0 ,} поскольку он имеет в два раза большую площадь, где генерируется фототок и через которую может протекать ток диода. По тому же аргументу он также будет иметь половину R _S последовательного сопротивления, связанного с вертикальным током; однако для кремниевых солнечных элементов большой площади масштабирование последовательного сопротивления, встречающегося при боковом токе, нелегко предсказать, поскольку оно будет зависеть в решающей степени от конструкции сетки (неясно, что означает «в остальном идентичный» в этом отношении). В зависимости от типа шунта, более крупный элемент может также иметь половину R _{SH ,} поскольку он имеет в два раза большую площадь, где могут возникать шунты; с другой стороны, если шунты возникают в основном по периметру, то R _SH будет уменьшаться в соответствии с изменением окружности, а не площади.

Поскольку изменения токов являются доминирующими и уравновешивают друг друга, напряжение холостого хода практически одинаково; V _OC начинает зависеть от размера ячейки только в том случае, если R _SH становится слишком низким. Для учета доминирования токов характеристическое уравнение часто записывается в терминах плотности тока , или тока, произведенного на единицу площади ячейки:

${\displaystyle J=J_{\text{L}}-J_{0}\left\{\exp \left[{\frac {q(V_{\text{out}}+Jr_{\text{S}})}{nkT}}\right]-1\right\}-{\frac {V_{\text{out}}+Jr_{\text{S}}}{r_{\text{SH}}}}}$

где

• J , плотность тока (ампер/см ² )
• J _L , плотность фотогенерированного тока (ампер/см ² )
• J ₀ , обратная плотность тока насыщения (ампер/см ² )
• r _S , удельное последовательное сопротивление (Ом·см ² )
• r _SH — удельное сопротивление шунта (Ом·см ² ).

Эта формулировка имеет несколько преимуществ. Одно из них заключается в том, что поскольку характеристики ячеек привязаны к общей площади поперечного сечения, их можно сравнивать для ячеек с разными физическими размерами. Хотя это имеет ограниченное преимущество в производственных условиях, где все ячейки, как правило, имеют одинаковый размер, это полезно в исследованиях и при сравнении ячеек между производителями. Другое преимущество заключается в том, что уравнение плотности естественным образом масштабирует значения параметров до схожих порядков величины, что может сделать численное извлечение проще и точнее даже при использовании наивных методов решения.

Существуют практические ограничения этой формулировки. Например, некоторые паразитические эффекты становятся более важными по мере уменьшения размеров клеток и могут влиять на извлеченные значения параметров. Рекомбинация и загрязнение соединения, как правило, наиболее выражены по периметру клетки, поэтому очень маленькие клетки могут демонстрировать более высокие значения J ₀ или более низкие значения R _SH, чем более крупные клетки, которые в остальном идентичны. В таких случаях сравнения между клетками следует проводить осторожно и с учетом этих эффектов.

Этот подход следует использовать только для сравнения солнечных элементов с сопоставимой компоновкой. Например, сравнение между в первую очередь квадратными солнечными элементами, такими как типичные кристаллические кремниевые солнечные элементы, и узкими, но длинными солнечными элементами, такими как типичные тонкопленочные солнечные элементы, может привести к неправильным предположениям, вызванным различными видами путей тока и, следовательно, влиянием, например, распределенного последовательного сопротивления, вносящего вклад в r _S . ^{[8] [9]} Макроархитектура солнечных элементов может привести к тому, что различные площади поверхности будут размещены в любом фиксированном объеме - особенно для тонкопленочных солнечных элементов и гибких солнечных элементов, которые могут допускать сильно извилистые складчатые структуры. Если объем является связывающим ограничением, то плотность эффективности, основанная на площади поверхности, может иметь меньшее значение.

Прозрачные проводящие электроды

Схема сбора заряда электродами солнечной ячейки. Свет проходит через прозрачный проводящий электрод, создавая пары электрон-дырка, которые собираются обоими электродами. ^[10]

Прозрачные проводящие электроды являются важнейшими компонентами солнечных элементов. Это либо непрерывная пленка оксида индия-олова , либо проводящая проволочная сеть, в которой провода являются коллекторами заряда, а пустоты между проводами прозрачны для света. Оптимальная плотность проволочной сети имеет важное значение для максимальной производительности солнечного элемента, поскольку более высокая плотность проводов блокирует пропускание света, а более низкая плотность проводов приводит к высоким потерям на рекомбинацию из-за большего расстояния, проходимого носителями заряда. ^[10]

Температура ячейки

Влияние температуры на вольт-амперные характеристики солнечного элемента

Температура влияет на характеристическое уравнение двумя способами: напрямую, через T в экспоненциальном члене, и косвенно, через свое влияние на I ₀ (строго говоря, температура влияет на все члены, но эти два гораздо значительнее, чем другие). В то время как увеличение T уменьшает величину экспоненты в характеристическом уравнении, значение I ₀ экспоненциально увеличивается с T . Чистый эффект заключается в линейном уменьшении V _OC (напряжения холостого хода) с ростом температуры. Величина этого уменьшения обратно пропорциональна V _OC ; то есть ячейки с более высокими значениями V _OC испытывают меньшее снижение напряжения с ростом температуры. Для большинства кристаллических кремниевых солнечных ячеек изменение V _OC с температурой составляет около −0,50%/°C, хотя скорость для кристаллических кремниевых ячеек с самой высокой эффективностью составляет около −0,35%/°C. Для сравнения, этот показатель для солнечных элементов на основе аморфного кремния составляет от -0,20 до -0,30%/°C в зависимости от способа изготовления элемента.

Количество фотогенерированного тока I _L немного увеличивается с ростом температуры из-за увеличения числа термически генерируемых носителей в ячейке. Однако этот эффект незначителен: около 0,065%/°C для ячеек из кристаллического кремния и 0,09% для ячеек из аморфного кремния.

Общее влияние температуры на эффективность ячейки можно вычислить, используя эти факторы в сочетании с характеристическим уравнением. Однако, поскольку изменение напряжения намного сильнее изменения тока, общее влияние на эффективность, как правило, аналогично влиянию напряжения. Большинство кристаллических кремниевых солнечных ячеек снижают эффективность на 0,50%/°C, а большинство аморфных ячеек снижают на 0,15−0,25%/°C. На рисунке выше показаны кривые IV, которые обычно можно увидеть для кристаллического кремниевого солнечного элемента при различных температурах.

Последовательное сопротивление

Влияние последовательного сопротивления на вольт-амперные характеристики солнечного элемента

По мере увеличения последовательного сопротивления падение напряжения между напряжением перехода и напряжением на клеммах становится больше для того же тока. В результате контролируемая током часть кривой IV начинает провисать к началу координат, вызывая значительное уменьшение и небольшое уменьшение I _SC , тока короткого замыкания. Очень высокие значения R _S также приведут к значительному уменьшению I _SC ; в этих режимах доминирует последовательное сопротивление, и поведение солнечного элемента напоминает поведение резистора. Эти эффекты показаны для кристаллических кремниевых солнечных элементов на кривых IV, показанных на рисунке справа. ${\displaystyle V_{\text{out}}}$

Мощность, теряемая через последовательное сопротивление, составляет . При освещении, когда и малы по сравнению с фототоком , потери мощности также увеличиваются квадратично с . Поэтому потери через последовательное сопротивление наиболее важны при высоких интенсивностях освещения. ${\displaystyle I_{\text{out}}^{2}R_{\text{S}}}$ ${\displaystyle I_{\text{D}}}$ ${\displaystyle I_{\text{SH}}}$ ${\displaystyle I_{\text{L}}}$ ${\displaystyle I_{\text{L}}}$

Сопротивление шунта

Влияние сопротивления шунта на вольт-амперные характеристики солнечного элемента

По мере уменьшения сопротивления шунта ток, отводимый через резистор шунта, увеличивается для заданного уровня напряжения перехода. В результате часть кривой IV, контролируемая напряжением, начинает провисать далеко от начала координат, что приводит к значительному уменьшению и небольшому уменьшению V _OC . Очень низкие значения R _SH приведут к значительному уменьшению V _OC . Как и в случае высокого последовательного сопротивления, плохо шунтированный солнечный элемент будет иметь рабочие характеристики, аналогичные характеристикам резистора. Эти эффекты показаны для солнечных элементов из кристаллического кремния на кривых IV, показанных на рисунке справа. ${\displaystyle I_{\text{out}}}$

Обратный ток насыщения

Влияние обратного тока насыщения на вольт-амперные характеристики солнечного элемента

Если предположить бесконечное сопротивление шунта, то характеристическое уравнение можно решить относительно V _OC :

${\displaystyle V_{\text{OC}}={\frac {kT}{q}}\ln \left({\frac {I_{\text{SC}}}{I_{0}}}+1\right).}$

Таким образом, увеличение I ₀ приводит к уменьшению V _OC пропорционально обратной величине логарифма увеличения. Это математически объясняет причину уменьшения V _OC , которое сопровождает увеличение температуры, описанное выше. Влияние обратного тока насыщения на кривую IV кристаллического кремниевого солнечного элемента показано на рисунке справа. Физически обратный ток насыщения является мерой «утечки» носителей через p–n-переход при обратном смещении. Эта утечка является результатом рекомбинации носителей в нейтральных областях по обе стороны от перехода.

Фактор идеальности

Влияние фактора идеальности на вольт-амперные характеристики солнечного элемента

Фактор идеальности (также называемый фактором излучения) — это подгоночный параметр, который описывает, насколько близко поведение диода соответствует предсказанному теорией, которая предполагает, что p–n-переход диода представляет собой бесконечную плоскость и в области пространственного заряда не происходит рекомбинации. Идеальное соответствие теории наблюдается при n = 1. Однако, когда рекомбинация в области пространственного заряда доминирует над другими рекомбинациями, n = 2. Эффект изменения фактора идеальности независимо от всех других параметров показан для кристаллического кремниевого солнечного элемента на кривых IV, показанных на рисунке справа.

Большинство солнечных элементов, которые довольно велики по сравнению с обычными диодами, хорошо приближаются к бесконечной плоскости и обычно демонстрируют почти идеальное поведение при стандартных условиях испытаний ( n ≈ 1 ). Однако при определенных условиях эксплуатации работа устройства может доминировать за счет рекомбинации в области пространственного заряда. Это характеризуется значительным увеличением I ₀ , а также увеличением фактора идеальности до n ≈ 2 . Последнее имеет тенденцию увеличивать выходное напряжение солнечного элемента, в то время как первое действует на его разрушение. Таким образом, чистый эффект представляет собой комбинацию увеличения напряжения, показанного для увеличения n на рисунке справа, и уменьшения напряжения, показанного для увеличения I ₀ на рисунке выше. Обычно I ₀ является более значимым фактором, и результатом является снижение напряжения.

Иногда наблюдается фактор идеальности, превышающий 2, что обычно объясняется наличием диода Шоттки или гетероперехода в солнечном элементе. ^[11] Наличие смещения гетероперехода снижает эффективность сбора солнечного элемента и может способствовать низкому фактору заполнения.

Другие модели

Хотя вышеприведенная модель является наиболее распространенной, были предложены и другие модели, такие как дискретная модель d1MxP. ^[12]

Смотрите также

• Электродвижущая сила § Солнечный элемент

Ссылки

1. NASA Solar System Exploration - Солнце: Факты и цифры Архивировано 2015-07-03 на Wayback Machine , получено 27 апреля 2011 г. "Эффективная температура ... 5777 К"
2. Карлсон, Д., Вронски, К. (1985). "Аморфные кремниевые солнечные элементы". Темы в прикладной физике: Аморфные полупроводники: Аморфные кремниевые солнечные элементы . Том 36. Springer Berlin / Heidelberg. стр. 287–329. doi :10.1007/3-540-16008-6_164. ISBN 978-3-540-16008-3.{{cite book}}: CS1 maint: multiple names: authors list (link) ISBN  9783540160083 , 9783540707516 .
3. "Солнечная ячейка под освещением". PV Lighthouse . Архивировано из оригинала 15 февраля 2016 г.
4. Эдуардо Лоренцо (1994). Солнечное электричество: проектирование фотоэлектрических систем. Progensa. ISBN 84-86505-55-0.
5. Антонио Луке и Стивен Хегедус (2003). Справочник по фотоэлектрической науке и технике. John Wiley and Sons. ISBN 0-471-49196-9.
6. Дженни Нельсон (2003). Физика солнечных элементов. Imperial College Press. ISBN 978-1-86094-340-9. Архивировано из оригинала 2009-12-31 . Получено 2010-10-13 .
7. exp представляет экспоненциальную функцию
8. AG Aberle и SR Wenham и MA Green, «Новый метод точных измерений сосредоточенного последовательного сопротивления солнечных элементов», Труды 23-й конференции специалистов IEEE по фотоэлектричеству, стр. 113-139, 1993.
9. Нильсен, Л.Д., Эффекты распределенного последовательного сопротивления в солнечных элементах, IEEE Transactions on Electron Devices, том 29, выпуск 5, стр. 821–827, 1982.
10. Kumar, Ankush (2017). «Прогнозирование эффективности солнечных элементов на основе прозрачных проводящих электродов». Журнал прикладной физики . 121 (1): 014502. Bibcode : 2017JAP...121a4502K. doi : 10.1063/1.4973117. ISSN  0021-8979.
11. Chavali, RVK; Wilcox, JR; Ray, B.; Gray, JL; Alam, MA (2014-05-01). "Коррелированные неидеальные эффекты темных и световых характеристик I #x2013;V в гетеропереходных солнечных элементах a-Si/c-Si". IEEE Journal of Photovoltaics . 4 (3): 763–771. doi :10.1109/JPHOTOV.2014.2307171. ISSN  2156-3381. S2CID  13449892.
12. Маркес Ламейриньяс, Рикардо А.; П. Коррейя В. Бернардо, Катарина; Н. Торрес, Жоау Паулу; Вейга, Хелена Изабель; Мендонса душ Сантуш, Педро (2023). «Моделирование влияния дефектов и трещин на работоспособность солнечных элементов с использованием дискретной модели d1MxP». Научные отчеты . 13 (1): 12490. doi : 10.1038/s41598-023-39769-0. ПМЦ 10393959 . ПМИД  37528136. 

Внешние ссылки

• Калькулятор эквивалентной схемы для фотоэлектрического маяка
• Объяснение химии — Солнечные элементы от chemistryexplained.com