Бикасательные квартики

Кривая Тротта и семь ее касательных. Остальные симметричны относительно поворотов на 90° вокруг начала координат.

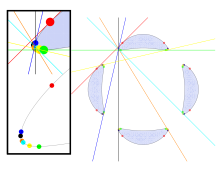
В теории алгебраических плоских кривых общая кривая четвертой степени имеет 28 бикасательных прямых, которые касаются кривой в двух местах. Эти прямые существуют в комплексной проективной плоскости , но можно определить кривые четвертой степени, для которых все 28 этих прямых имеют действительные числа в качестве своих координат и, следовательно, принадлежат евклидовой плоскости .

Явная квартика с двадцатью восемью действительными касательными к двум точкам была впервые дана Плюккером (1839) ^[1] Как показал Плюккер, число действительных касательных к двум точкам любой квартики должно быть равно 28, 16 или числу меньше 9. Другая квартика с 28 действительными касательными к двум точкам может быть образована геометрическим местом центров эллипсов с фиксированными длинами осей, касательными к двум непараллельным прямым. ^[2] Сиода (1995) дал другую конструкцию квартики с двадцатью восемью касательными к двум точкам, образованной путем проецирования кубической поверхности ; двадцать семь касательных к кривой Сиоды являются действительными, а двадцать восьмая является прямой на бесконечности в проективной плоскости.

Пример

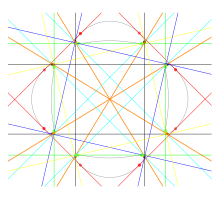
Кривая Тротта , еще одна кривая с 28 действительными бикасательными, представляет собой множество точек ( x , y ), удовлетворяющих полиномиальному уравнению четвертой степени

\displaystyle 144(x^{4}+y^{4})-225(x^{2}+y^{2})+350x^{2}y^{2}+81=0.

Эти точки образуют неособую кривую четвертого порядка, которая имеет род три и двадцать восемь действительных касательных к двум точкам . ^[3]

Как и в примерах Плюккера и Блюма и Гинанда, кривая Тротта имеет четыре разделенных овала, максимальное число для кривой степени четыре, и, следовательно, является М-кривой . Четыре овала можно сгруппировать в шесть различных пар овалов; для каждой пары овалов есть четыре касательных, касающихся обоих овалов в паре, две, которые разделяют два овала, и две, которые этого не делают. Кроме того, каждый овал ограничивает невыпуклую область плоскости и имеет одну касательную, охватывающую невыпуклую часть его границы.

Соединения с другими структурами

Двойственная кривая к кривой четвертого порядка имеет 28 действительных обыкновенных двойных точек, двойственных 28 бикасательным прямой кривой.

28 бикасательных квартики также можно поставить в соответствие с символами вида

{\begin{bmatrix}a&b&c\\d&e&f\\\end{bmatrix}}

где $a, b, c, d, e, f$ — все это ноль или единица и где

ad+be+cf=1\ (\operatorname {mod} \ 2).

^[4]

Существует 64 варианта выбора для $a, b, c, d, e, f$ , но только 28 из этих вариантов дают нечетную сумму. Можно также интерпретировать $a, b, c$ как однородные координаты точки плоскости Фано , а $d, e, f$ как координаты прямой в той же конечной проективной плоскости; условие нечетности суммы эквивалентно требованию, чтобы точка и прямая не касались друг друга, и существует 28 различных пар точки и прямой, которые не касаются друг друга.

Точки и линии плоскости Фано, которые не пересекаются с неинцидентной парой точка-линия, образуют треугольник, а бикасательные квартики рассматриваются как соответствующие 28 треугольникам плоскости Фано. ^[5] Граф Леви плоскости Фано — это граф Хивуда , в котором треугольники плоскости Фано представлены 6-циклами. 28 6-циклов графа Хивуда, в свою очередь, соответствуют 28 вершинам графа Коксетера . [ ^6]

28 бикасательных квартики также соответствуют парам из 56 прямых на поверхности дель Пеццо степени 2 [ 5 ^] и 28 нечетным тета-характеристикам .

27 прямых на кубической кривой и 28 бикасательных на квартике вместе со 120 трикасательными плоскостями канонической секстической кривой рода 4 образуют « троицу » в смысле Владимира Арнольда , в частности, форму соответствия Маккея ^[7]^[8]^[9], и могут быть связаны со многими другими объектами, включая E7 _и E8 _, как обсуждалось в троицах .

Примечания

^ См., например, Грей (1982).
^ Блюм и Гуинанд (1964).
^ Тротт (1997).
^ Риман (1876); Кейли (1879).
^ ab Manivel (2006).
^ Дейтер, Итало Дж. (2011), «От графа Коксетера к графу Клейна», Журнал теории графов , 70 : 1–9, arXiv : 1002.1960 , doi : 10.1002/jgt.20597, S2CID 754481.
^ le Bruyn, Lieven (17 июня 2008 г.), Троицы Арнольда, архивировано из оригинала 2011-04-11
^ Арнольд 1997, стр. 13 – Арнольд, Владимир, 1997, Торонтские лекции, Лекция 2: Симплектизация, комплексификация и математические троицы, июнь 1997 (последнее обновление август 1998). TeX, PostScript, PDF
^ (Маккей и Себбар 2007, стр. 11)

Ссылки

Блюм, Р.; Гуинанд, А.П. (1964). «Квартика с 28 действительными касательными к двум». Канадский математический вестник . 7 (3): 399–404. doi :10.4153/cmb-1964-038-6.
Кейли, Артур (1879), «О касательных к двум четвертого порядка», Salmon's Higher Plane Curves , стр. 387–389, В сборнике математических работ Артура Кейли , под ред. Эндрю Рассела Форсайта, The University Press, 1896, т. 11, стр. 221–223.
Грей, Джереми (1982), «Из истории простой группы», The Mathematical Intelligencer , 4 (2): 59–67, CiteSeerX 10.1.1.163.2944 , doi :10.1007/BF03023483, MR 0672918, S2CID 14602496. Перепечатано в Levy, Silvio, ed. (1999), The Eightfold Way , MSRI Publications, т. 35, Cambridge University Press, стр. 115–131, ISBN 0-521-66066-1, г-н 1722415.
Манивел, Л. (2006), «Конфигурации линий и модели алгебр Ли», Журнал алгебры , 304 (1): 457–486, arXiv : math/0507118 , doi : 10.1016/j.jalgebra.2006.04.029 , S2CID 17374533.
Маккей, Джон; Себбар, Абделла (2007). «Повторяемые функции: Введение». Frontiers in Number Theory, Physics, and Geometry II . стр. 373–386. doi :10.1007/978-3-540-30308-4_10. ISBN 978-3-540-30307-7.
Плюкер, Дж. (1839), Теория алгебраической кривой: gegrundet auf eine neue Behandlungsweise der analytischen Geometrie , Берлин: Адольф Маркус.
Риман, GFB (1876), "Zur Theorie der Abel'schen Funktionen für den Fall p = 3", Ges. Верке , Лейпциг, стр. 456–472.{{citation}}: CS1 maint: отсутствует местоположение издателя ( ссылка ). Как цитирует Кейли.
Сиода, Тецудзи (1995), «Преобразования Вейерштрасса и кубические поверхности» (PDF) , Commentarii Mathematici Universitatis Sancti Pauli , 44 (1): 109–128, MR 1336422
Тротт, Майкл (1997), «Применение базиса Грёбнера к трём задачам геометрии», Mathematica в образовании и исследованиях , 6 (1): 15–28.