В конечной геометрии плоскость Фано (названная в честь Джино Фано ) — это конечная проективная плоскость с наименьшим возможным числом точек и прямых: 7 точек и 7 прямых, с 3 точками на каждой прямой и 3 прямыми, проходящими через каждую точку. Эти точки и прямые не могут существовать с такой схемой инцидентности в евклидовой геометрии , но им можно задать координаты с помощью конечного поля с двумя элементами. Стандартное обозначение для этой плоскости, как члена семейства проективных пространств , — PG(2, 2) . Здесь PG означает « проективная геометрия », первый параметр — геометрическая размерность (это плоскость размерности 2), а второй параметр — порядок (количество точек на прямой, минус один).
Плоскость Фано является примером конечной структуры инцидентности , поэтому многие ее свойства могут быть установлены с помощью комбинаторных методов и других инструментов, используемых при изучении геометрий инцидентности . Поскольку это проективное пространство, алгебраические методы также могут быть эффективными инструментами при ее изучении.
В другом использовании плоскость Фано — это проективная плоскость, которая никогда не удовлетворяет аксиоме Фано ; другими словами, диагональные точки полного четырехугольника всегда коллинеарны. [1] «Плоскость» Фано из 7 точек и прямых — это «плоскость» Фано.
Плоскость Фано может быть построена с помощью линейной алгебры как проективная плоскость над конечным полем с двумя элементами. Аналогично можно построить проективные плоскости над любым другим конечным полем, причем плоскость Фано будет наименьшей.
Используя стандартную конструкцию проективных пространств через однородные координаты , семь точек плоскости Фано могут быть помечены семью ненулевыми упорядоченными тройками двоичных цифр 001, 010, 011, 100, 101, 110 и 111. Это можно сделать таким образом, что для каждых двух точек p и q третья точка на прямой pq будет иметь метку, образованную сложением меток p и q по модулю 2 цифра за цифрой (например, 010 и 111 дают 101). Другими словами, точки плоскости Фано соответствуют ненулевым точкам конечного векторного пространства размерности 3 над конечным полем порядка 2.
Благодаря такому построению плоскость Фано считается плоскостью Дезарга , даже несмотря на то, что плоскость слишком мала, чтобы содержать невырожденную конфигурацию Дезарга (для которой требуется 10 точек и 10 прямых).
Прямым плоскости Фано также можно задать однородные координаты, снова используя ненулевые тройки двоичных цифр. В этой системе координат точка инцидентна прямой, если координата для точки и координата для прямой имеют четное число позиций, в которых они обе имеют ненулевые биты: например, точка 101 принадлежит прямой 111, потому что они имеют ненулевые биты в двух общих позициях. В терминах базовой линейной алгебры точка принадлежит прямой, если внутреннее произведение векторов, представляющих точку и прямую, равно нулю.
Линии можно разделить на три типа.
Альтернативно, 7 точек плоскости соответствуют 7 нетождественным элементам группы ( Z 2 ) 3 = Z 2 × Z 2 × Z 2 . Прямые плоскости соответствуют подгруппам порядка 4, изоморфным Z 2 × Z 2 . Группа автоморфизмов GL(3, 2) группы (Z 2 ) 3 является группой автоморфизмов плоскости Фано и имеет порядок 168.
Как и любая структура инцидентности, граф Леви плоскости Фано является двудольным графом , вершины одной части представляют точки, а другой — линии, с двумя вершинами, соединенными, если соответствующая точка и линия инцидентны . Этот конкретный граф является связным кубическим графом (регулярным степени 3), имеет обхват 6 , и каждая часть содержит 7 вершин. Это граф Хивуда , уникальная 6-клетка . [2]
Коллинеация , автоморфизм или симметрия плоскости Фано — это перестановка 7 точек, которая сохраняет коллинеарность: то есть, она переводит коллинеарные точки (на одной прямой) в коллинеарные точки. Согласно Фундаментальной теореме проективной геометрии , полная группа коллинеаций (или группа автоморфизмов , или группа симметрии ) — это проективная линейная группа PGL(3, 2) , [a] Hirschfeld 1979, стр. 131 [3]
Это хорошо известная группа порядка 168 = 2 3 ·3 ·7, следующая неабелева простая группа после A 5 порядка 60 (упорядоченная по размеру).
Как группа перестановок, действующая на 7 точек плоскости, группа коллинеаций является дважды транзитивной , что означает, что любая упорядоченная пара точек может быть отображена по крайней мере одной коллинеацией в любую другую упорядоченную пару точек. [4] (См. ниже.)
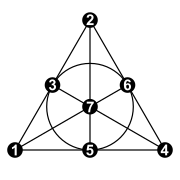
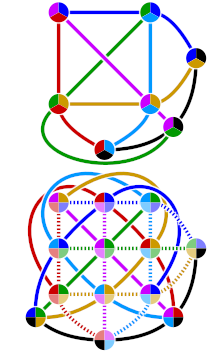
Коллинеации также можно рассматривать как сохраняющие цвет автоморфизмы графа Хивуда (см. рисунок).
F 8 является расширением поля степени три для F 2 , поэтому точки плоскости Фано можно отождествить с F 8 ∖ {0} . Группа симметрии может быть записана как PGL(3, 2) = Aut( P 2 F 2 ) . Аналогично, PSL(2, 7) = Aut( P 1 F 7 ) . Существует связь между базовыми объектами, P 2 F 2 и P 1 F 7 , называемая картой «колыбель для кошки». Раскрасьте семь линий плоскости Фано ROYGBIV, поместите пальцы в двумерное проективное пространство в окружающем 3-пространстве и вытяните их, как в детской игре «колыбель для кошки». Вы получите полный граф на семи вершинах с семью цветными треугольниками (проективными линиями). Отсутствующее начало координат F 8 будет в центре внутреннего семиугольника. Теперь обозначьте эту точку как ∞ и потяните ее назад к началу координат. Можно записать биекцию из F 7 ∪ {∞} в F 8 . Положим x ∞ = 0 и отправим наклон k ↦ x ∞ + x k ∈ F 8 ≅ F 2 [ x ] / ( x 3 + x + 1) , где теперь x k помечает вершины K 7 с помощью раскраски ребер , отметив, что F×
8— циклическая группа порядка 7. Симметрии P 1 F 7 — это преобразования Мёбиуса , а основные преобразования — это отражения (порядок 2, k ↦ −1/ k ), переносы (порядок 7, k ↦ k + 1 ) и удвоение (порядок 3, поскольку 2 3 = 1 , k ↦ 2 k ). Соответствующие симметрии на плоскости Фано — это соответственно перестановка вершин, поворот графа и поворот треугольников.
Биекция между множеством точек и множеством линий, сохраняющая инцидентность, называется двойственностью , а двойственность второго порядка называется полярностью . [ 5]
Дуальности можно рассматривать в контексте графа Хивуда как автоморфизмы, меняющие цвет. Пример полярности дается отражением относительно вертикальной линии, которая делит пополам представление графа Хивуда, приведенное справа. [6] Существование этой полярности показывает, что плоскость Фано является самодуальной . Это также является непосредственным следствием симметрии между точками и линиями в определении отношения инцидентности в терминах однородных координат, как подробно описано в предыдущем разделе.
Группа перестановок из 7 точек имеет 6 классов сопряженности .
Каждая из этих четырех структур цикла определяет один класс сопряженности:
Перестановка идентичности
21 перестановка с двумя 2-циклами
42 перестановки с 4-циклом и 2-циклом
56 перестановок с двумя 3-циклами48 перестановок с полным 7-циклом образуют два различных класса сопряженности с 24 элементами:
A отображается в B , B в C , C в D. Тогда D находится на той же прямой, что и A и B.
A отображается в B , B в C , C в D. Тогда D находится на той же прямой, что и A и C.(Полный список см. здесь.)
Число неэквивалентных раскрасок плоскости Фано цветами можно вычислить, подставив число структур циклов в теорему о перечислении Полиа . Это число раскрасок равно (последовательность A241929 в OEIS ).
В любой проективной плоскости набор из четырех точек, никакие три из которых не лежат на одной прямой, и шесть прямых, соединяющих пары этих точек, образуют конфигурацию, известную как полный четырехугольник . Прямые называются сторонами , а пары сторон, которые не пересекаются ни в одной из четырех точек, называются противоположными сторонами . Точки, в которых пересекаются противоположные стороны, называются диагональными точками , и их три. [7]
Если эта конфигурация лежит в проективной плоскости и три диагональные точки коллинеарны, то семь точек и семь прямых расширенной конфигурации образуют подплоскость проективной плоскости, которая изоморфна плоскости Фано и называется подплоскостью Фано .
Известный результат, полученный Эндрю М. Глисоном, гласит, что если каждый полный четырехугольник в конечной проективной плоскости продолжается до подплоскости Фано (то есть имеет коллинеарные диагональные точки), то плоскость является дезарговой. [8] Глисон назвал любую проективную плоскость, удовлетворяющую этому условию, плоскостью Фано, тем самым создав некоторую путаницу с современной терминологией. Чтобы усугубить путаницу, аксиома Фано утверждает, что диагональные точки полного четырехугольника никогда не являются коллинеарными, условие, которое выполняется в евклидовых и действительных проективных плоскостях. Таким образом, то, что Глисон назвал плоскостями Фано, не удовлетворяет аксиоме Фано. [9]
Плоскость Фано содержит следующее количество конфигураций точек и линий разных типов. Для каждого типа конфигурации количество копий конфигурации, умноженное на количество симметрий плоскости, которые сохраняют конфигурацию неизменной, равно 168, размеру всей группы коллинеаций, при условии, что каждая копия может быть отображена в любую другую копию (см. теорему о стабилизаторе орбиты ). Поскольку плоскость Фано является самодвойственной, эти конфигурации поступают в двойственных парах, и можно показать, что количество коллинеаций, фиксирующих конфигурацию, равно количеству коллинеаций, фиксирующих ее двойственную конфигурацию.
Плоскость Фано является примером ( n 3 ) -конфигурации, то есть набора из n точек и n прямых с тремя точками на каждой прямой и тремя прямыми, проходящими через каждую точку. Плоскость Фано, (7 3 )-конфигурация, является уникальной и является наименьшей такой конфигурацией. [11] Согласно теореме Штейница [12] конфигурации этого типа могут быть реализованы в евклидовой плоскости, имеющей не более одной кривой линии (все остальные линии лежат на евклидовых прямых). [13]
Плоскость Фано — это небольшая симметричная блочная конструкция , а именно 2-(7, 3, 1) -конструкция. Точки конструкции — это точки плоскости, а блоки конструкции — это линии плоскости. [14] Таким образом, это ценный пример в теории (блочной) конструкции.
С точками, помеченными 0, 1, 2, ..., 6, линии (как наборы точек) являются переносами плоскостного разностного множества (7, 3, 1) , заданного {0, 1, 3} в группе Z / 7 Z . [14] С линиями, помеченными ℓ 0 , ..., ℓ 6 , матрица инцидентности (таблица) задается следующим образом:
Плоскость Фано, как блочная конструкция, является системой троек Штейнера . [15] Как таковая, она может быть задана структурой квазигруппы . Эта квазигруппа совпадает с мультипликативной структурой, определяемой единичными октонионами e1, e2, ..., e7 ( опуская 1 ) , если знаки произведений октонионов игнорируются (Baez 2002) .
Матроид Фано F 7 формируется путем взятия точек плоскости Фано в качестве базового множества и трехэлементных неколлинеарных подмножеств в качестве базисов.
Плоскость Фано является одним из важных примеров в теории структур матроидов . Исключение плоскости Фано как минора матроида необходимо для характеристики нескольких важных классов матроидов, таких как регулярные , графические и кографические.
Если разбить одну линию на три двухточечные линии, то получится «не-Фановская конфигурация», которая может быть вложена в действительную плоскость. Это еще один важный пример в теории матроидов, поскольку он должен быть исключен для выполнения многих теорем.
Плоскость Фано может быть расширена в третьем измерении, чтобы сформировать трехмерное проективное пространство, обозначаемое PG(3, 2) . Оно имеет 15 точек, 35 прямых и 15 плоскостей и является наименьшим трехмерным проективным пространством . [16] Оно также обладает следующими свойствами: [17]
