Формальный язык

Последовательность слов, образованная по определенным правилам

Структура синтаксически правильного, хотя и бессмысленного, английского предложения «Бесцветные зеленые идеи яростно спят» ( исторический пример из Хомского , 1957).

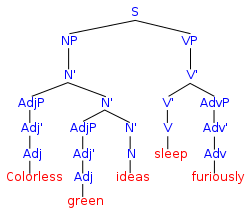
В логике , математике , информатике и лингвистике формальный язык состоит из слов , буквы которых взяты из алфавита и правильно сформированы в соответствии с определенным набором правил, называемых формальной грамматикой .

Алфавит формального языка состоит из символов, букв или токенов , которые объединяются в строки, называемые словами. ^[1] Слова, принадлежащие к определенному формальному языку, иногда называют правильно сформированными словами или правильно сформированными формулами . Формальный язык часто определяется посредством формальной грамматики , такой как регулярная грамматика или контекстно-свободная грамматика , которая состоит из правил формирования .

В информатике формальные языки используются, среди прочего, в качестве основы для определения грамматики языков программирования и формализованных версий подмножеств естественных языков, в которых слова языка представляют понятия, связанные со значениями или семантикой . В теории сложности вычислений проблемы принятия решений обычно определяются как формальные языки, а классы сложности определяются как наборы формальных языков, которые могут анализироваться машинами с ограниченной вычислительной мощностью. В логике и основах математики формальные языки используются для представления синтаксиса аксиоматических систем , а математический формализм — это философия, согласно которой вся математика может быть сведена к синтаксическому манипулированию формальными языками таким образом.

Область формальной теории языка изучает прежде всего чисто синтаксические аспекты таких языков, то есть их внутренние структурные закономерности. Формальная теория языка возникла из лингвистики как способ понимания синтаксических закономерностей естественных языков .

История

В 17 веке Готфрид Лейбниц придумал и описал «characterica Universalis» , универсальный и формальный язык, в котором использовались пиктограммы . Позже Карл Фридрих Гаусс исследовал проблему кодов Гаусса . ^[2]

Готтлоб Фреге попытался реализовать идеи Лейбница с помощью системы обозначений, впервые изложенной в Begriffsschrift (1879) и более полно развитой в его двухтомном Grundgesetze der Arithmetik (1893/1903). ^[3] Это описывало «формальный язык чистого языка». ^[4]

В первой половине 20 века произошло несколько событий, касающихся формальных языков. В период с 1906 по 1914 год Аксель Туэ опубликовал четыре статьи, посвященные словам и языку. Последняя из них представила то, что Эмиль Пост позже назвал «системами Туэ», и дала ранний пример неразрешимой проблемы . ^[5] Позже Пост использовал эту статью как основу для доказательства в 1947 году, «что проблема слов для полугрупп рекурсивно неразрешима», ^[6] и позже разработал каноническую систему для создания формальных языков.

В 1907 году в Вене Леонардо Торрес Кеведо ввёл формальный язык описания механических чертежей (механических устройств) . Он опубликовал «Sobre un sistema de notaciones y símbolos destinados a facilitar la descripción de las máquinas» («О системе обозначений и символов, предназначенных для облегчения описания машин»). ^[7] Хайнц Земанек оценил его как эквивалент языка программирования для числового программного управления станками. ^[8]

Ноам Хомский разработал абстрактное представление формальных и естественных языков, известное как иерархия Хомского . ^[9] В 1959 году Джон Бэкус разработал форму Бэкуса-Наура для описания синтаксиса языка программирования высокого уровня, следуя своей работе по созданию FORTRAN . ^[10] Питер Наур был секретарем/редактором отчета ALGOL60, в котором он использовал форму Бэкуса-Наура для описания формальной части ALGOL60.

Слова над алфавитом

Алфавитом в контексте формальных языков может быть любой набор ; его элементы называются буквами . Алфавит может содержать бесконечное количество элементов; ^{[примечание 1]} однако большинство определений в теории формального языка определяют алфавиты с конечным числом элементов, и многие результаты применимы только к ним. Часто имеет смысл использовать алфавит в обычном смысле этого слова или, в более общем смысле, любую конечную кодировку символов , такую ​​как ASCII или Unicode .

Словом в алфавите может быть любая конечная последовательность (т. е. строка ) букв. Множество всех слов в алфавите Σ обычно обозначается Σ ^* (с использованием звезды Клини ). Длина слова – это количество букв, из которых оно состоит. В любом алфавите существует только одно слово длины 0, пустое слово , которое часто обозначается e, ε, λ или даже Λ. Путем конкатенации можно объединить два слова в новое слово, длина которого равна сумме длин исходных слов. Результатом объединения слова с пустым словом является исходное слово.

В некоторых приложениях, особенно в логике , алфавит также известен как словарь , а слова известны как формулы или предложения ; это разрушает метафору буквы/слова и заменяет ее метафорой слова/предложения.

Определение

Формальный язык L над алфавитом Σ — это подмножество Σ ^* , то есть набор слов над этим алфавитом. Иногда наборы слов группируются в выражения, тогда как правила и ограничения могут быть сформулированы для создания «правильно сформированных выражений».

В информатике и математике, которые обычно не имеют дело с естественными языками , прилагательное «формальный» часто опускается как избыточное.

Хотя теория формального языка обычно занимается формальными языками, которые описываются некоторыми синтаксическими правилами, фактическое определение понятия «формальный язык» такое же, как указано выше: набор (возможно, бесконечный) набор строк конечной длины, составленный из заданного алфавита. не больше и не меньше. На практике существует множество языков, которые можно описать правилами, например обычные языки или контекстно-свободные языки . Понятие формальной грамматики может быть ближе к интуитивному понятию «языка», описываемому синтаксическими правилами. Злоупотребляя этим определением, часто думают, что конкретный формальный язык оснащен формальной грамматикой, которая его описывает.

Примеры

Следующие правила описывают формальный язык  L над алфавитом Σ = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, +, =}:

• Каждая непустая строка, которая не содержит «+» или «=" и не начинается с «0», находится в  L .
• Строка «0» находится в  L .
• Строка, содержащая "=", находится в  L тогда и только тогда, когда существует ровно один "=", и она разделяет две допустимые строки  L .
• Строка, содержащая "+", но не "=", находится в  L тогда и только тогда, когда каждый "+" в строке разделяет две допустимые строки  L .
• В L нет строк,  отличных от тех, которые подразумеваются предыдущими правилами.

Согласно этим правилам, строка «23+4=555» находится в  L , а строка «=234=+» — нет. Этот формальный язык выражает натуральные числа , правильное сложение и правильное сложение равенств, но выражает только то, как они выглядят (их синтаксис ), а не то, что они означают ( семантика ). Например, нигде в этих правилах нет указания на то, что «0» означает число ноль, «+» означает сложение, «23+4=555» является ложным и т. д.

Конструкции

Для конечных языков можно явно перечислить все правильно построенные слова. Например, мы можем описать язык  L просто как L  = {a, b, ab, cba}. Вырожденный случай этой конструкции — пустой язык , вообще не содержащий слов ( L  =  ∅ ).

Однако даже в конечном (непустом) алфавите, таком как Σ = {a, b}, существует бесконечное количество слов конечной длины, которые потенциально могут быть выражены: «a», «abb», «ababba», « aaababbbbaab", .... Следовательно, формальные языки обычно бесконечны, и описать бесконечный формальный язык не так просто, как написать L  = {a, b, ab, cba}. Вот несколько примеров формальных языков:

• L = Σ ^* — множество всех слов над Σ;
• L = {a} ^* = {a ⁿ }, где n пробегает натуральные числа и «a ⁿ » означает «a», повторенное n раз (это набор слов, состоящий только из символа «a»);
• набор синтаксически правильных программ на данном языке программирования (синтаксис которых обычно определяется контекстно-свободной грамматикой );
• набор входных данных, на которых останавливается определенная машина Тьюринга ; или
• набор максимальных строк буквенно-цифровых символов ASCII в этой строке, т. е.
  набор {the, set, of, Maximum, strings, алфавитно-цифровые, ASCII, символы, on, this, line, i, e}.

Формализмы спецификации языка

Формальные языки используются в качестве инструментов во многих дисциплинах. Однако формальная теория языка редко занимается конкретными языками (за исключением примеров), а в основном занимается изучением различных типов формализмов для описания языков. Например, язык может быть задан как

• эти строки, порожденные некоторой формальной грамматикой ;
• те строки, которые описаны или соответствуют определенному регулярному выражению ;
• эти строки принимаются некоторым автоматом , например машиной Тьюринга или конечным автоматом ;
• те строки, для которых некоторая процедура принятия решения ( алгоритм , задающий последовательность связанных вопросов ДА/НЕТ) дает ответ ДА.

Типичные вопросы, задаваемые по поводу таких формализмов, включают:

• Какова их выразительная сила? (Может ли формализм X описать каждый язык, который может описать формализм Y ? Может ли он описать другие языки?)
• Какова их узнаваемость? (Насколько сложно решить, принадлежит ли данное слово языку, описываемому формализмом X ?)
• В чем их сопоставимость? (Насколько сложно решить, являются ли два языка, один из которых описан в формализме X , другой в формализме Y или снова в X , на самом деле одним и тем же языком?).

На удивление часто ответом на эти проблемы принятия решения является «это вообще невозможно сделать» или «это чрезвычайно дорого» (с характеристикой того, насколько дорого). Таким образом, теория формального языка является основной областью применения теории вычислимости и теории сложности . Формальные языки могут быть классифицированы в иерархии Хомского на основе выразительной силы их порождающей грамматики, а также сложности их распознающего автомата . Контекстно-свободные грамматики и регулярные грамматики обеспечивают хороший компромисс между выразительностью и простотой синтаксического анализа и широко используются в практических приложениях.

Операции над языками

Некоторые операции над языками являются общими. Сюда входят стандартные операции над множествами, такие как объединение, пересечение и дополнение. Другой класс операций — это поэлементное применение строковых операций.

Примеры: предположим, что и — это языки, основанные на некотором общем алфавите . ${\displaystyle L_{1}}$ ${\displaystyle L_{2}}$ ${\displaystyle \Sigma }$

• Конкатенация состоит из всех строк вида где — строка из и — строка из . ${\displaystyle L_{1}\cdot L_{2}}$ ${\displaystyle vw}$ ${\displaystyle v}$ ${\displaystyle L_{1}}$ ${\displaystyle w}$ ${\displaystyle L_{2}}$
• Пересечение и состоит из всех строк, содержащихся в обоих языках . ${\displaystyle L_{1}\cap L_{2}}$ ${\displaystyle L_{1}}$ ${\displaystyle L_{2}}$
• Дополнение по отношению к состоит из всех строк , которых нет в . ${\displaystyle \neg L_{1}}$ ${\displaystyle L_{1}}$ ${\displaystyle \Sigma }$ ${\displaystyle \Sigma }$ ${\displaystyle L_{1}}$
• Звезда Клини : язык, состоящий из всех слов, представляющих собой конкатенацию нуля или более слов исходного языка;
• Реверс :
  • Пусть ε — пустое слово, тогда , и ${\displaystyle \varepsilon ^{R}=\varepsilon }$
  • для каждого непустого слова (где элементы некоторого алфавита) пусть , ${\displaystyle w=\sigma _{1}\cdots \sigma _{n}}$ ${\displaystyle \sigma _{1},\ldots ,\sigma _{n}}$ ${\displaystyle w^{R}=\sigma _{n}\cdots \sigma _{1}}$
  • тогда для формального языка . ${\displaystyle L}$ ${\displaystyle L^{R}=\{w^{R}\mid w\in L\}}$
• Струнный гомоморфизм

Такие строковые операции используются для исследования свойств замыкания классов языков. Класс языков закрывается при определенной операции, когда операция, примененная к языкам в этом классе, всегда снова создает язык того же класса. Например, известно, что контекстно-свободные языки замкнуты при объединении, конкатенации и пересечении с обычными языками , но не закрыты при пересечении или дополнении. Теория трио и абстрактных семей языков самостоятельно изучает наиболее распространенные свойства замыкания языковых семей. ^[11]

Приложения

Языки программирования

Компилятор обычно состоит из двух отдельных компонентов. Лексический анализатор , иногда создаваемый таким инструментом, как lex, идентифицирует токены грамматики языка программирования, например, идентификаторы или ключевые слова , числовые и строковые литералы, знаки пунктуации и символы операторов, которые сами задаются более простым формальным языком, обычно с помощью обычных выражения . На самом базовом концептуальном уровне синтаксический анализатор , иногда создаваемый генератором синтаксического анализатора , например yacc, пытается решить, является ли исходная программа синтаксически допустимой, то есть правильно ли она сформирована по отношению к грамматике языка программирования, для которого был создан компилятор.

Конечно, компиляторы делают больше, чем просто анализируют исходный код — они обычно переводят его в некоторый исполняемый формат. Из-за этого синтаксический анализатор обычно выводит больше, чем ответ «да/нет», обычно это абстрактное синтаксическое дерево . Это используется последующими этапами компилятора для создания исполняемого файла , содержащего машинный код , который выполняется непосредственно на оборудовании, или некоторый промежуточный код , для выполнения которого требуется виртуальная машина .

Формальные теории, системы и доказательства

Эта диаграмма показывает синтаксические подразделения внутри формальной системы . Строки символов можно условно разделить на бессмысленные и правильно построенные формулы . Множество корректных формул делится на теоремы и нетеоремы.

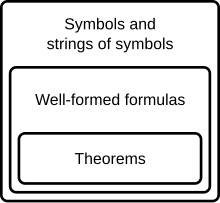
В математической логике формальная теория — это набор предложений , выраженных на формальном языке.

Формальная система (также называемая логическим исчислением или логической системой ) состоит из формального языка вместе с дедуктивным аппаратом (также называемым дедуктивной системой ). Дедуктивный аппарат может состоять из набора правил преобразования , которые можно интерпретировать как действительные правила вывода, или набора аксиом , или иметь и то, и другое. Формальная система используется для получения одного выражения из одного или нескольких других выражений. Хотя формальный язык можно идентифицировать по его формулам, формальную систему нельзя также идентифицировать по ее теоремам. Две формальные системы , и все они могут иметь одни и те же теоремы, но при этом отличаться каким-то существенным теоретико-доказательным образом (например, формула A может быть синтаксическим следствием формулы B в одной, но не в другой). ${\displaystyle {\mathcal {FS}}}$ ${\displaystyle {\mathcal {FS'}}}$

Формальное доказательство или вывод — это конечная последовательность правильно построенных формул (которые можно интерпретировать как предложения или суждения ), каждая из которых является аксиомой или следует из предыдущих формул последовательности по правилу вывода . Последнее предложение в последовательности представляет собой теорему формальной системы. Формальные доказательства полезны, потому что их теоремы можно интерпретировать как истинные предложения.

Интерпретации и модели

Формальные языки полностью синтаксичны по своей природе, но им может быть придана семантика , придающая значение элементам языка. Например, в математической логике набор возможных формул конкретной логики представляет собой формальный язык, и интерпретация присваивает каждой формуле значение — обычно значение истинности .

Изучение интерпретаций формальных языков называется формальной семантикой . В математической логике это часто делается с точки зрения теории моделей . В теории моделей термины, которые встречаются в формуле, интерпретируются как объекты внутри математических структур , а фиксированные правила композиционной интерпретации определяют, как значение истинности формулы может быть получено из интерпретации ее членов; Модель формулы — это интерпретация терминов, при которой формула становится истинной .

Смотрите также

• Комбинаторика по словам
• Формальный метод
• Бесплатный моноид
• Грамматическая основа
• Математические обозначения
• Строка (информатика)

Примечания

1. Например, логика первого порядка часто выражается с использованием алфавита, который, помимо таких символов, как ∧, ¬, ∀ и круглых скобок, содержит бесконечное количество элементов x ₀ ,  x ₁ ,  x ₂ ,… которые играют роль переменных.

Рекомендации

Цитаты

1. См., например , Регицци, Стефано Креспи (2009). Формальные языки и компиляция. Тексты по информатике. Спрингер. п. 8. Бибкод : 2009flc..книга.....C. ISBN 9781848820500. Алфавит – это конечное множество
2. «В предыстории формальной теории языка: языки Гаусса». Январь 1992 года . Проверено 30 апреля 2021 г.
3. "Готтлоб Фреге". 5 декабря 2019 года . Проверено 30 апреля 2021 г.
4. Мартин Дэвис (1995). «Влияние математической логики на информатику». В Рольфе Херкене (ред.). Универсальная машина Тьюринга: обзор за полвека . Спрингер. п. 290. ИСБН 978-3-211-82637-9.
5. «Документ Туэ 1914 года: перевод» (PDF) . 28 августа 2013 г. Архивировано (PDF) из оригинала 30 апреля 2021 г. . Проверено 30 апреля 2021 г.
6. "Эмиль Леон Пост". Сентябрь 2001 года . Проверено 30 апреля 2021 г.
7. Торрес Кеведо, Леонардо. Sobre un sistema de notaciones y símbolos destinados a facilitar la descripción de las máquinas, (pdf), стр. 25–30, Revista de Obras Públicas, 17 января 1907 г.
8. Брюдерер, Герберт (2021). «Глобальная эволюция компьютерных технологий». Вехи в аналоговых и цифровых вычислениях . Спрингер. п. 1212. ИСБН 978-3030409739.
9. Ягер, Герхард; Роджерс, Джеймс (19 июля 2012 г.). «Теория формального языка: уточнение иерархии Хомского». Философские труды Королевского общества Б. 367 (1598): 1956–1970. дои : 10.1098/rstb.2012.0077. ПМЦ 3367686 . ПМИД  22688632. 
10. "Джон Уорнер Бэкус". Февраль 2016 года . Проверено 30 апреля 2021 г.
11. Хопкрофт и Ульман (1979), Глава 11: Свойства замыкания семейств языков.

Источники

Цитируемые работы

• Хопкрофт, Джон Э .; Уллман, Джеффри Д. (1979). Введение в теорию автоматов, языки и вычисления . Ридинг, Массачусетс: Издательство Addison-Wesley. ISBN 81-7808-347-7.

Общие ссылки

• А. Г. Гамильтон, Логика для математиков , издательство Кембриджского университета , 1978, ISBN 0-521-21838-1 . 
• Сеймур Гинзбург , Алгебраические и теоретико-автоматные свойства формальных языков , Северная Голландия, 1975, ISBN 0-7204-2506-9 . 
• Майкл А. Харрисон , Введение в теорию формального языка , Аддисон-Уэсли, 1978.
• Раутенберг, Вольфганг (2010). Краткое введение в математическую логику (3-е изд.). Нью-Йорк: Springer Science + Business Media . дои : 10.1007/978-1-4419-1221-3. ISBN 978-1-4419-1220-6.
• Гжегож Розенберг , Арто Саломаа , Справочник по формальным языкам: Том I-III , Springer, 1997, ISBN 3-540-61486-9 . 
• Патрик Суппес, Введение в логику , Д. Ван Ностранд, 1957, ISBN 0-442-08072-7 . 

Внешние ссылки

• «Формальный язык», Математическая энциклопедия , EMS Press , 2001 [1994]
• Университет Мэриленда , Формальные определения языка
• Джеймс Пауэр, «Заметки по теории формального языка и синтаксическому анализу». Архивировано 21 ноября 2007 г. в Wayback Machine , 29 ноября 2002 г.
• Черновики некоторых глав «Справочника по теории формального языка», Vol. 1–3, Г. Розенберг и А. Саломаа (ред.), Springer Verlag , (1997):
  • Александру Матееску и Арто Саломаа, «Предисловие» в томе 1, стр. v – viii, и «Формальные языки: введение и краткий обзор», глава 1 в томе. 1, стр. 1–39.
  • Шэн Юй, «Обычные языки», глава 2 в томе. 1
  • Жан-Мишель Отебер, Жан Берстель, Люк Боассон, «Контекстно-свободные языки и автоматы с выталкиванием вниз», глава 3 в томе. 1
  • Кристиан Чоффрут и Юхани Кархумяки, «Комбинаторика слов», глава 6 в томе. 1
  • Теро Харью и Юхани Кархумяки, «Морфизмы», глава 7 в томе. 1, стр. 439–510.
  • Жан-Эрик Пин, «Синтаксические полугруппы», глава 10 в томе. 1, стр. 679–746.
  • М. Крочемор и К. Ханкарт, «Автоматы для сопоставления шаблонов», глава 9 в томе. 2
  • Дора Джаммаррези, Антонио Рестиво, «Двумерные языки», глава 4 в томе. 3, стр. 215–267.