Доказательства малой теоремы Ферма

В этой статье собраны различные доказательства малой теоремы Ферма , которая утверждает, что

${\displaystyle a^{p}\equiv a{\pmod {p}}}$

для каждого простого числа p и каждого целого числа a (см. модульную арифметику ).

Упрощения

Некоторые из приведенных ниже доказательств малой теоремы Ферма основаны на двух упрощениях.

Первое — мы можем предположить, что a находится в диапазоне 0 ≤ a ≤ p − 1. Это простое следствие законов модульной арифметики ; мы просто говорим, что сначала можем уменьшить a по модулю  p . Это согласуется с уменьшением по модулю  p , как можно проверить. ${\displaystyle a^{p}}$

Во-вторых, достаточно доказать, что

${\displaystyle a^{p-1}\equiv 1{\pmod {p}}}$

для a в диапазоне 1 ≤ a ≤ p − 1. Действительно, если предыдущее утверждение верно для такого a , умножение обеих сторон на a дает исходную форму теоремы,

${\displaystyle a^{p}\equiv a{\pmod {p}}}$

С другой стороны, если a = 0 или a = 1 , теорема тривиально выполняется.

Комбинаторные доказательства

Доказательство путем подсчета ожерелий

Это, пожалуй, самое простое известное доказательство, требующее наименьшего математического бэкграунда. Это привлекательный пример комбинаторного доказательства ( доказательства, которое включает подсчет набора объектов двумя разными способами ).

Приведенное здесь доказательство является адаптацией доказательства Голомба . ^[1]

Для простоты предположим, что a — положительное целое число . Рассмотрим все возможные строки из p символов, используя алфавит с a различными символами. Общее количество таких строк равно a ^p , поскольку для каждой из p позиций существует a возможностей (см. правило произведения ).

Например, если p  = 5 и a = 2 , то мы можем использовать алфавит с двумя символами (скажем, A и B ), и тогда будет 2 ⁵  = 32 строки длины 5:

ААААА , ААААБ , АААБА , АААББ , ААБАА , ААБАБ , ААББА , ААБББ ,

АБААА , АБААБ , АБАБА , АБАБ , АББА , АББАБ , АББА , АББББ ,

БАААА , БАААБ , БААБА , БААББ , БАБАА , БАБАБ , БАББА , БАБББ ,

ББААА , ББААБ , ББАБА , ББАББ , БББАА , БББАБ , ББББА , БББББ .

Ниже мы покажем, что если удалить из списка строки, состоящие из одного символа (в нашем примере AAAAA и BBBBB ), то оставшиеся a ^p − a строк можно организовать в группы, каждая из которых содержит ровно p строк. Из этого следует, что a ^p − a делится на  p .

Ожерелья

Ожерелье, представляющее семь различных строк ( ABCBAAC , BCBAACA , CBAACAB , BAACABC , AACABCB , ACABCBA , CABCBAA )

Ожерелье, представляющее собой только одну нить ( AAAAAAA )

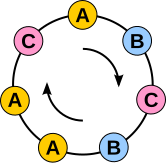
Давайте представим, что каждая такая строка представляет собой ожерелье . То есть, мы соединяем два конца строки вместе и рассматриваем две строки как одно и то же ожерелье, если мы можем повернуть одну строку, чтобы получить вторую строку; в этом случае мы скажем, что две строки являются друзьями . В нашем примере следующие строки все являются друзьями:

ААААБ , АААБА , ААБАА , АБААА , БАААА .

В целом каждая строка следующего списка соответствует одному ожерелью, а весь список охватывает все 32 строки.

ААААБ , АААБА , ААБАА , АБААА , БАААА ,

АААББ , ААББА , АББАА , ББААА , БАААБ ,

ААБАБ , АБАБА , БАБАА , АБААБ , БААБА ,

ААБББ , АБББА , БББАА , ББААБ , БААББ ,

АБАББ , БАББА , АББАБ , ББАБА , БАБАБ ,

АББББ , ББББА , БББАБ , БАБББ ,​​

ААААА ,

БББББ .

Обратите внимание, что в приведенном выше списке каждое ожерелье с более чем одним символом представлено 5 различными строками, а количество ожерелий, представленных только одной строкой, равно 2, т.е. является количеством различных символов. Таким образом, список очень ясно показывает, почему 32 − 2 делится на 5 .

Чтобы определить, сколько друзей у заданной строки S, можно использовать следующее правило :

Если S состоит из нескольких копий строки T , и T сама по себе не может быть разбита на повторяющиеся строки, то число друзей S (включая саму S ) равно длине T.

Например, предположим, что мы начинаем со строки S  =  ​​ABBABBABBABB , которая состоит из нескольких копий более короткой строки T  =  ABB . Если мы вращаем ее по одному символу за раз, мы получаем следующие 3 строки:

АББАББАББАБ ,

БАБАБАБАБАББА ,

БАБАБАБАБАБАБ .

Других нет, поскольку ABB состоит ровно из 3 символов и не может быть разбита на дальнейшие повторяющиеся строки.

Завершение доказательства

Используя приведенное выше правило, мы можем довольно легко завершить доказательство малой теоремы Ферма следующим образом. Наш начальный пул строк ^p можно разделить на две категории:

• Некоторые строки содержат p одинаковых символов. Их ровно a , по одному на каждый символ в алфавите. (В нашем примере это строки AAAAA и BBBBB .)
• Остальные строки используют по крайней мере два различных символа из алфавита. Если мы можем разбить S на повторяющиеся копии некоторой строки T , длина T должна делить длину S . Но поскольку длина S является простым числом p , единственно возможной длиной для T также является p . Следовательно, приведенное выше правило говорит нам, что у S есть ровно p друзей (включая саму S ).

Вторая категория содержит строки p ⁻ a , и они могут быть организованы в группы по p строк, по одной группе на каждое ожерелье. Следовательно, p − ^a должно делиться на p , как и было обещано.

Доказательство с использованием динамических систем

Это доказательство использует некоторые основные концепции динамических систем . ^[2]

Начнем с рассмотрения семейства функций T _n ( x ), где n ≥ 2 — целое число , отображающее интервал [0, 1] на себя по формуле

${\displaystyle T_{n}(x)={\begin{cases}\{nx\}&0\leq x<1,\\1&x=1,\end{cases}}}$

где { y } обозначает дробную часть y . Например , функция T ₃ ( x ) проиллюстрирована ниже:

Пример функции T _n

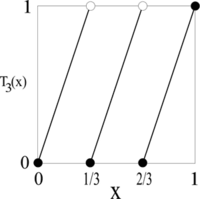
Число x ₀ называется неподвижной точкой функции f ( x ), если f ( x ₀ ) = x ₀ ; другими словами, если f оставляет x ₀ неподвижным. Неподвижные точки функции можно легко найти графически: это просто координаты x точек, где график f ( x ) пересекает график прямой y = x . Например, неподвижные точки функции T 3 ₍ x ) — это 0, 1/2 и 1; они отмечены черными кружками на следующей диаграмме:

Неподвижные точки функции T _n

Нам потребуются следующие две леммы.

Лемма 1. Для любого n ≥ 2 функция T _n ( x ) имеет ровно n неподвижных точек.

Доказательство. На рисунке выше есть 3 неподвижные точки, и тот же самый геометрический аргумент применим для любого n ≥ 2.

Лемма 2. Для любых положительных целых чисел n и m и любого 0 ≤ x ≤ 1,

${\displaystyle T_{m}(T_{n}(x))=T_{mn}(x).}$

Другими словами, T _mn ( x ) представляет собой композицию T n ₍ x ) и T _m ( x ).

Доказательство. Доказательство этой леммы несложно, но нам нужно быть немного осторожнее с конечной точкой x = 1. Для этой точки лемма, очевидно, верна, поскольку

${\displaystyle T_{m}(T_{n}(1))=T_{m}(1)=1=T_{mn}(1).}$

Итак, предположим, что 0 ≤ x < 1. В этом случае,

${\displaystyle T_{n}(x)=\{nx\}<1,}$

поэтому T _m ( T _n ( x )) определяется как

${\displaystyle T_{m}(T_{n}(x))=\{m\{nx\}\}.}$

Поэтому нам действительно нужно показать, что

${\displaystyle \{m\{nx\}\}=\{mnx\}.}$

Для этого заметим, что { nx } = nx − k , где k — целая часть nx ; тогда

${\displaystyle \{m\{nx\}\}=\{mnx-mk\}=\{mnx\},}$

поскольку mk — целое число.

Теперь давайте начнем доказательство малой теоремы Ферма, изучая функцию T _{a ^p} ( x ). Предположим, что a ≥ 2. Из леммы 1 мы знаем, что она имеет a ^p неподвижных точек. Из леммы 2 мы знаем, что

${\displaystyle T_{a^{p}}(x)=\underbrace {T_{a}(T_{a}(\cdots T_{a}(x)\cdots ))} _{p{\text{ times}}},}$

поэтому любая фиксированная точка T _a ( x ) автоматически является фиксированной точкой T _{a ^p} ( x ).

Нас интересуют неподвижные точки T _{a ^p} ( x ), которые не являются неподвижными точками T _a ( x ). Назовем множество таких точек S . В S имеется p − ^a точек , поскольку по лемме 1 снова T _a ( x ) имеет ровно a неподвижных точек. Следующая диаграмма иллюстрирует ситуацию для a = 3 и p = 2. Черные кружки — это точки S , которых 3 ² − 3 = 6.

Неподвижные точки в множестве S

Основная идея доказательства теперь состоит в том, чтобы разбить множество S на его орбиты относительно T _a . Это означает, что мы выбираем точку x ₀ в S и многократно применяем к ней T _a (x), чтобы получить последовательность точек

${\displaystyle x_{0},T_{a}(x_{0}),T_{a}(T_{a}(x_{0})),T_{a}(T_{a}(T_{a}(x_{0}))),\ldots .}$

Эта последовательность называется орбитой x ₀ при T _a . По лемме 2 эта последовательность может быть переписана как

${\displaystyle x_{0},T_{a}(x_{0}),T_{a^{2}}(x_{0}),T_{a^{3}}(x_{0}),\ldots .}$

_{Поскольку мы} предполагаем, что _x0 является фиксированной точкой Tap ( _x ) , после ^_p шагов мы достигаем ^_Tap ( x0 ₎ = x0 , и с этого момента последовательность повторяется.

Однако последовательность не может начать повторяться раньше этого. Если бы это произошло, длина повторяющейся секции должна была бы быть делителем p , поэтому она должна была бы быть 1 (так как p — простое число). Но это противоречит нашему предположению, что x ₀ не является неподвижной точкой T _a .

Другими словами, орбита содержит ровно p различных точек. Это справедливо для каждой орбиты S. Следовательно, множество S , которое содержит a ^p  −  a точек, можно разбить на орбиты, каждая из которых содержит p точек, поэтому a ^p  −  a делится на p .

(Это доказательство по сути то же самое, что и доказательство с подсчетом ожерелий, приведенное выше, просто рассматриваемое через другую призму: можно представить интервал [0, 1] как заданный последовательностями цифр в основании a (наше различие между 0 и 1 соответствует знакомому различию между представлением целых чисел, заканчивающихся на «.0000...» и «.9999...»). T _{a ⁿ} равнозначно сдвигу такой последовательности на n цифр. Неподвижные точки этого будут последовательностями, которые являются циклическими с периодом, делящим n . В частности, неподвижные точки T _{a ^p} можно рассматривать как ожерелья длины p , причем T _{a ⁿ} соответствует повороту таких ожерелий на n точек.

Это доказательство можно было бы представить и без различения 0 и 1, просто используя полуоткрытый интервал [0, 1); тогда T _n имел бы только n − 1 неподвижную точку, но T _{a ^p} − T _a все равно приводил бы к a ^p − a , как и требовалось.)

Многочленные доказательства

Доказательства с использованием биномиальной теоремы

Доказательство 1

Это доказательство, принадлежащее Эйлеру ^[3], использует индукцию для доказательства теоремы для всех целых чисел a  ≥ 0 .

Базовый шаг, что 0 ^p  ≡ 0 (mod  p ) , тривиален. Далее, мы должны показать, что если теорема верна для a  =  k , то она также верна для a  =  k  + 1 . Для этого индуктивного шага нам понадобится следующая лемма.

Лемма . Для любых целых чисел x и y и любого простого числа p , ( x  +  y ) ^p  ≡  x ^p  +  y ^p  (mod  p ) .

Лемма — случай мечты первокурсника . Оставив доказательство на потом, приступим к индукции.

Доказательство . Предположим, что k ^p ≡ k (mod p ), и рассмотрим ( k +1) ^p . По лемме имеем

${\displaystyle (k+1)^{p}\equiv k^{p}+1^{p}{\pmod {p}}.}$

Используя гипотезу индукции, мы имеем, что k ^p ≡ k (mod p ); и, тривиально, 1 ^p = 1. Таким образом,

${\displaystyle (k+1)^{p}\equiv k+1{\pmod {p}},}$

что является утверждением теоремы для a = k +1. ∎

Чтобы доказать лемму, мы должны ввести биномиальную теорему , которая утверждает, что для любого положительного целого числа n ,

${\displaystyle (x+y)^{n}=\sum _{i=0}^{n}{n \choose i}x^{n-i}y^{i},}$

где коэффициенты являются биномиальными коэффициентами ,

${\displaystyle {n \choose i}={\frac {n!}{i!(n-i)!}},}$

описанная в терминах факториальной функции, n ! = 1×2×3×⋯× n .

Доказательство леммы. Рассмотрим биномиальный коэффициент, когда показатель степени — простое число p :

${\displaystyle {p \choose i}={\frac {p!}{i!(p-i)!}}}$

Биномиальные коэффициенты все целые числа. Числитель содержит множитель p по определению факториала. Когда 0 < i < p , ни один из членов в знаменателе не включает множитель p (полагаясь на простоту p ), оставляя сам коэффициент иметь простой множитель p из числителя, подразумевая, что

${\displaystyle {p \choose i}\equiv 0{\pmod {p}},\qquad 0<i<p.}$

По модулю p это исключает все, кроме первого и последнего членов суммы в правой части биномиальной теоремы для простого числа p . ∎

Простота числа p существенна для леммы; в противном случае мы имеем примеры вроде

${\displaystyle {4 \choose 2}=6,}$

которое не делится на 4.

Доказательство 2

Используя лемму, имеем:

${\displaystyle k^{p}\equiv ((k-1)+1)^{p}\equiv (k-1)^{p}+1\equiv ((k-2)+1)^{p}+1\equiv (k-2)^{p}+2\equiv \dots \equiv k{\pmod {p}}}$.

Доказательство с использованием полиномиального разложения

Доказательство, впервые обнаруженное Лейбницем (который его не опубликовал) ^[4] и позднее переоткрытое Эйлером ^[3] , представляет собой очень простое применение теоремы о многочленах , которая гласит:

${\displaystyle (x_{1}+x_{2}+\cdots +x_{m})^{n}=\sum _{k_{1},k_{2},\dots ,k_{m} \atop k_{1}+k_{2}+\dots +k_{m}=n}{n \choose k_{1},k_{2},\ldots ,k_{m}}x_{1}^{k_{1}}x_{2}^{k_{2}}\cdots x_{m}^{k_{m}}}$

где

${\displaystyle {n \choose k_{1},k_{2},\ldots ,k_{m}}={\frac {n!}{k_{1}!k_{2}!\dots k_{m}!}}}$

и суммирование берется по всем последовательностям неотрицательных целых индексов k ₁ , k ₂ , ..., k _m таким образом, что сумма всех k _i равна n .

Таким образом, если мы выразим a как сумму единиц, то получим

${\displaystyle a^{p}=(1+1+...+1)^{p}=\sum _{k_{1},k_{2},\dots ,k_{a} \atop k_{1}+k_{2}+\dots +k_{a}=p}{p \choose k_{1},k_{2},\ldots ,k_{a}}}$

Очевидно, если p — простое число и если k _j не равно p ни для какого j , то мы имеем

${\displaystyle {p \choose k_{1},k_{2},\ldots ,k_{a}}\equiv 0{\pmod {p}},}$

и если k _j равно p для некоторого j, то

${\displaystyle {p \choose k_{1},k_{2},\ldots ,k_{a}}=1.}$

Поскольку существует ровно a элементов, таких что k _j  =  p для некоторого j , то теорема следует.

(Это доказательство по сути является более грубым вариантом доказательства с подсчетом ожерелий, приведенного ранее; коэффициенты полиномов подсчитывают количество способов, которыми строка может быть переставлена ​​в произвольные анаграммы, в то время как аргумент с ожерельем подсчитывает количество способов, которыми строка может быть повернута в циклические анаграммы. То есть тот факт, что нетривиальные коэффициенты полиномов здесь делятся на p, можно рассматривать как следствие того факта, что каждое нетривиальное ожерелье длины p может быть развернуто в строку p многими способами.

Это многочленное разложение, конечно, по сути, лежит в основе приведенного выше доказательства, основанного на биномиальной теореме.)

Доказательство с использованием расширений продукта мощности

Аддитивно-комбинаторное доказательство, основанное на формальных степенных разложениях, было дано Гедрюсом Алкаускасом. ^[5] Это доказательство не использует ни алгоритм Евклида , ни биномиальную теорему , а вместо этого использует формальные степенные ряды с рациональными коэффициентами.

Доказательство как частный случай теоремы Эйлера

Это доказательство ^{[3] [6],} открытое Джеймсом Айвори ^[7] и переоткрытое Дирихле ^[8] , требует некоторых знаний в области модульной арифметики .

Предположим, что a положительно и не делится на p .

Идея состоит в том, что если мы запишем последовательность чисел

и сократить каждый из них по модулю p , то полученная последовательность оказывается перестановкой

Следовательно, если мы перемножим числа в каждой последовательности, результаты должны быть идентичны по модулю p :

${\displaystyle a\times 2a\times 3a\times \cdots \times (p-1)a\equiv 1\times 2\times 3\times \cdots \times (p-1){\pmod {p}}.}$

Собирая вместе члены a, получаем

${\displaystyle a^{p-1}(p-1)!\equiv (p-1)!{\pmod {p}}.}$

Наконец, мы можем «сократить» числа 1, 2, ..., p − 1 с обеих сторон этого уравнения, получив

${\displaystyle a^{p-1}\equiv 1{\pmod {p}}.}$

В приведенном выше доказательстве есть два шага, которые нам необходимо обосновать:

• Почему элементы последовательности ( A ), приведенные по модулю p , являются перестановкой ( B ), и
• Почему допустимо «отменять» в условиях модульной арифметики.

Мы докажем это ниже; давайте сначала рассмотрим пример этого доказательства в действии.

Пример

Если a  = 3 и p  = 7 , то рассматриваемая последовательность имеет вид

${\displaystyle 3,6,9,12,15,18;}$

сокращение по модулю 7 дает

${\displaystyle 3,6,2,5,1,4,}$

который является просто перестановкой

${\displaystyle 1,2,3,4,5,6.}$

Умножение их вместе дает

${\displaystyle 3\times 6\times 9\times 12\times 15\times 18\equiv 3\times 6\times 2\times 5\times 1\times 4\equiv 1\times 2\times 3\times 4\times 5\times 6{\pmod {7}};}$

то есть,

${\displaystyle 3^{6}(1\times 2\times 3\times 4\times 5\times 6)\equiv (1\times 2\times 3\times 4\times 5\times 6){\pmod {7}}.}$

Сокращая 1 × 2 × 3 × 4 × 5 × 6, получаем

${\displaystyle 3^{6}\equiv 1{\pmod {7}},}$

что является малой теоремой Ферма для случая a  = 3 и  p  = 7 .

Закон об отмене

Давайте сначала объясним, почему в определенных ситуациях допустимо «отменять». Точное утверждение выглядит следующим образом. Если u , x , и  y являются целыми числами, и u не делится на простое число p , и если

тогда мы можем «отменить» u , чтобы получить

Наше использование этого закона сокращения в приведенном выше доказательстве малой теоремы Ферма было обоснованным, поскольку числа 1 , 2, ..., p  − 1 определенно не делятся на p (на самом деле они меньше p ).

Мы можем легко доказать закон сокращения, используя лемму Евклида , которая в общем случае гласит, что если простое число p делит произведение ab (где a и b — целые числа), то p должно делить a или b . Действительно, утверждение ( C ) просто означает, что p делит ux − uy = u ( x − y ) . Поскольку p — простое число, которое не делит u , лемма Евклида говорит нам, что оно должно делить x  −  y ; то есть выполняется ( D ).

Обратите внимание, что условия, при которых выполняется закон сокращения, довольно строгие, и это объясняет, почему малая теорема Ферма требует, чтобы p было простым числом. Например, 2×2 ≡ 2×5 (mod 6) , но неверно, что 2 ≡ 5 (mod 6) . Однако выполняется следующее обобщение закона сокращения: если u , x , y , и z являются целыми числами, если u и z являются взаимно простыми , и если

${\displaystyle ux\equiv uy{\pmod {z}},}$

тогда мы можем «отменить» u , чтобы получить

${\displaystyle x\equiv y{\pmod {z}}.}$

Это следует из обобщения леммы Евклида .

Свойство перегруппировки

Наконец, мы должны объяснить, почему последовательность

${\displaystyle a,2a,3a,\ldots ,(p-1)a,}$

при уменьшении по модулю p становится перестановкой последовательности

${\displaystyle 1,2,3,\ldots ,p-1.}$

Начнем с того, что ни один из членов a , 2 a , ..., ( p  − 1) a не может быть сравним с нулем по модулю p , поскольку если k — одно из чисел 1, 2, ...,  p  − 1 , то k взаимно просто с p , как и a , поэтому лемма Евклида гласит, что ka не имеет общих множителей с p . Поэтому, по крайней мере, мы знаем, что числа a , 2 a , ..., ( p  − 1) a , приведенные по модулю p , должны быть найдены среди чисел 1, 2, 3, ...,  p  − 1 .

Более того, числа a , 2 a , ..., ( p  − 1) a должны быть различны после приведения их к модулю p , потому что если

${\displaystyle ka\equiv ma{\pmod {p}},}$

где k и m — одно из чисел 1, 2, ...,  p  − 1 , то закон сокращения говорит нам, что

${\displaystyle k\equiv m{\pmod {p}}.}$

Так как и k, и m находятся между 1 и p  − 1 , они должны быть равны. Следовательно, члены a , 2 a , ..., ( p  − 1) a при сокращении по модулю p должны быть различны. Подводя итог: когда мы сокращаем p  − 1 чисел a , 2 a , ..., ( p  − 1) a по модулю p , мы получаем различные члены последовательности 1 ,  2 , ...,  p  − 1. Так как их ровно p  − 1 , единственная возможность состоит в том, что первые являются перестановкой последних.

Приложения к теореме Эйлера

Этот метод также может быть использован для доказательства теоремы Эйлера с небольшим изменением, заключающимся в том, что числа от 1 до p − 1 заменяются числами, меньшими и взаимно простыми с некоторым числом m (не обязательно простым). Как свойство перестановки, так и закон сокращения (в обобщенной форме, упомянутой выше) по-прежнему выполняются и могут быть использованы.

Например, если m = 10 , то числа, меньшие  m и взаимно простые с m, — это 1 , 3 , 7 и 9. Таким образом, имеем:

${\displaystyle a\times 3a\times 7a\times 9a\equiv 1\times 3\times 7\times 9{\pmod {10}}.}$

Поэтому,

${\displaystyle {a^{\varphi (10)}}\equiv 1{\pmod {10}}.}$

Доказательство как следствие критерия Эйлера

Доказательства с использованием теории групп

Стандартная проверка

Это доказательство ^[9] требует самых основных элементов теории групп .

Идея состоит в том, чтобы признать, что множество G  = {1, 2, ..., p − 1 }, с операцией умножения (взятой по модулю p ), образует группу . Единственная аксиома группы, для проверки которой требуются некоторые усилия, заключается в том, что каждый элемент G обратим. Приняв это на веру на данный момент, предположим, что a находится в диапазоне 1 ≤ a ≤ p − 1 , то есть a является элементом G . Пусть k будет порядком a , то есть k является наименьшим положительным целым числом, таким что a ^k  ≡ 1 (mod  p ) . Тогда числа 1, a , a ² , ..., a ^{k  −1 ,} приведенные по модулю  p , образуют подгруппу G  , порядок которой равен  k , и поэтому по теореме Лагранжа k делит порядок G , который равен p  − 1 . Таким образом, p  − 1 =  km для некоторого положительного целого числа m , и тогда

${\displaystyle a^{p-1}\equiv a^{km}\equiv (a^{k})^{m}\equiv 1^{m}\equiv 1{\pmod {p}}.}$

Чтобы доказать, что каждый элемент b из G обратим, мы можем действовать следующим образом. Во-первых, b взаимно прост с p . Таким образом, тождество Безу гарантирует нам, что существуют целые числа x и y, такие что bx  +  py  = 1. Читая это равенство по модулю p , мы видим, что x является обратным для b , поскольку bx  ≡ 1 (mod  p ) . Следовательно, каждый элемент G обратим. Итак, как было отмечено ранее, G является группой.

Например, когда p = 11 , обратные значения каждого элемента задаются следующим образом:

Доказательство Эйлера

Если мы возьмем предыдущее доказательство и, вместо использования теоремы Лагранжа, попытаемся доказать его в этой конкретной ситуации, то получим третье доказательство Эйлера, которое он счел более естественным. ^{[10] [11]} Пусть A — множество, элементами которого являются числа 1, a , a ² , ..., a ^{k  − 1 ,} приведенные по модулю  p . Если A  =  G , то k  =  p  − 1 и, следовательно, k делит p  −1 . В противном случае существует некоторое b ₁  ∈  G \ A .

Пусть A ₁ — множество, элементами которого являются числа b ₁ , ab ₁ , a ² b ₁ , ..., a ^{k − 1} b _{1 ,} приведенные к модулю  p . Тогда A ₁ имеет k различных элементов, поскольку в противном случае существовало бы два различных числа m , n  ∈ {0, 1, ..., k − 1 ^} , таких что a ^m b ₁ ≡ an ^b ₁ (mod p ) , что невозможно, поскольку отсюда следовало бы, что a ^m ≡ an (mod p ) . С другой стороны, никакой элемент A ₁ не может быть элементом A , потому ^что в противном случае существовали бы числа m , n  ∈ {0, 1, ..., k  − 1 ^{} такие} , что a ^m b ₁ ≡ an (mod p ) , и тогда b ₁ ≡ an a ^{k − m} ≡ an ^{+ k − m} (mod p ) , что невозможно, так как b ₁ ∉ A .

Итак, множество A ∪ A ₁ имеет 2 k элементов. Если оно окажется равным  G , то 2 k  =  p  −1 и, следовательно, k делит p  −1 . В противном случае найдется некоторое b ₂  ∈  G \( A ∪ A ₁ ) , и мы можем начать все заново, определив A ₂ как множество, элементами которого являются числа b ₂ , ab ₂ , a ² b ₂ , ..., a ^{k  − 1} b _{2 ,} приведенные по модулю  p . Поскольку G конечно, этот процесс должен остановиться в какой-то момент, и это доказывает, что k делит p  − 1 .

Например, если a = 5 и p = 13 , то, поскольку

• 5 ²  = 25 ≡ 12 (мод 13) ,
• 5 ³  = 125 ≡ 8 (мод 13) ,
• 5 ⁴  = 625 ≡ 1 (мод 13) ,

мы имеем k  = 4 и A  = {1, 5, 8, 12 }. Очевидно, A  ≠  G  = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 }. Пусть b ₁ будет элементом G \ A ; например, возьмем b ₁  = 2 . Тогда, поскольку

• 2×1 = 2 ,
• 2×5 = 10 ,
• 2×8 = 16 ≡ 3 (мод 13) ,
• 2×12 = 24 ≡ 11 (мод 13) ,

имеем A ₁  = {2, 3, 10, 11 }. Очевидно, A ∪ A ₁ ≠ G . Пусть b ₂ — элемент G \( A ∪ A ₁ ) ; например, возьмем b ₂ = 4 . Тогда, поскольку

• 4×1 = 4 ,
• 4×5 = 20 ≡ 7 (мод 13) ,
• 4×8 = 32 ≡ 6 (мод 13) ,
• 4×12 = 48 ≡ 9 (мод 13) ,

имеем A ₂  = {4, 6, 7, 9 }. И теперь G  =  A ∪ A ₁ ∪ A ₂ .

Обратите внимание, что множества A , A ₁ и т. д . на самом деле являются смежными классами A в G.

Примечания

1. Голомб, Соломон В. (1956), «Комбинаторное доказательство «малой» теоремы Ферма» (PDF) , American Mathematical Monthly , 63 (10): 718, doi :10.2307/2309563, JSTOR  2309563
2. Ига, Кевин (2003), «Доказательство малой теоремы Ферма с помощью динамических систем», Mathematics Magazine , 76 (1): 48–51, doi :10.2307/3219132, JSTOR  3219132
3. Диксон, Леонард Юджин (2005) [1919], "Теоремы Ферма и Вильсона, обобщения и обратные им; симметричные функции от 1, 2, ..., p  − 1 по модулю p ", История теории чисел , т. I, Дувр , ISBN 978-0-486-44232-7, ЗБЛ  1214.11001
4. Вакка, Джованни (1894), «Intorno alla prima dimostrazione di un teorema di Fermat», Bibliotheca Mathematica , 2-я серия (на итальянском языке), 8 (2): 46–48
5. Алкаускас, Гиедрюс (2009), «Любопытное доказательство малой теоремы Ферма», American Mathematical Monthly , 116 (4): 362–364, arXiv : 0801.0805 , doi : 10.4169/193009709x470236, JSTOR  40391097
6. Харди, Г. Х .; Райт, Э. М. (2008), «Теорема Ферма и ее следствия», Введение в теорию чисел (6-е изд.), Oxford University Press , ISBN 978-0-19-921986-5
7. Айвори, Джеймс (1806), «Демонстрация теоремы о простых числах», Математический репозиторий , Новая серия, 1 (II): 6–8
8. Лежен Дирихле, Питер Густав (1828), «Démonstrations nouvelles de quelques théorèmes relatifs aux nombres», Journal für die reine und angewandte Mathematik (на французском языке), 3 : 390–393
9. Вейль, Андре ; Розенлихт, Максвелл (1979), «§ VIII», Теория чисел для начинающих , Springer-Verlag , doi : 10.1007/978-1-4612-9957-8, ISBN 978-0-387-90381-1, ЗБЛ  0405.10001
10. Вайль, Андре (2007) [1984], "§ III.VI", Теория чисел: подход через историю; от Хаммурапи до Лежандра , Биркхойзер , ISBN 978-0-8176-4565-6, Збл  1149.01013
11. Эйлер, Леонард (1761), «Theoremata circa residua ex Divisione Potestatum Relicta» (PDF) , Novi Commentarii Academiae Scientiarum Petropolitanae (на латыни), 7 : 49–82