
В математике временной ряд — это ряд точек данных , проиндексированных (или перечисленных, или графически отображенных) во временном порядке. Чаще всего временной ряд — это последовательность , взятая в последовательных равноотстоящих точках времени. Таким образом, это последовательность дискретных временных данных. Примерами временных рядов являются высоты океанских приливов , количество солнечных пятен и дневное значение закрытия индекса Dow Jones Industrial Average .
Временной ряд очень часто изображается с помощью графика хода событий (который является временной линейной диаграммой ). Временные ряды используются в статистике , обработке сигналов , распознавании образов , эконометрике , математических финансах , прогнозировании погоды , предсказании землетрясений , электроэнцефалографии , технике управления , астрономии , технике связи и в значительной степени в любой области прикладной науки и техники , которая включает временные измерения.
Анализ временных рядов включает методы анализа данных временных рядов с целью извлечения значимых статистических данных и других характеристик данных. Прогнозирование временных рядов — это использование модели для прогнозирования будущих значений на основе ранее наблюдавшихся значений. Как правило, данные временных рядов моделируются как стохастический процесс . Хотя регрессионный анализ часто применяется таким образом, чтобы проверить взаимосвязи между одним или несколькими различными временными рядами, этот тип анализа обычно не называется «анализом временных рядов», который относится, в частности, к взаимосвязям между различными точками во времени в пределах одного ряда.
Данные временных рядов имеют естественный временной порядок. Это отличает анализ временных рядов от исследований поперечного сечения , в которых нет естественного порядка наблюдений (например, объяснение заработной платы людей ссылкой на их соответствующие уровни образования, где данные людей могут быть введены в любом порядке). Анализ временных рядов также отличается от анализа пространственных данных , где наблюдения обычно связаны с географическим положением (например, учет цен на жилье по местоположению, а также по внутренним характеристикам домов). Стохастическая модель для временных рядов, как правило, отражает тот факт, что наблюдения, близкие друг к другу во времени, будут более тесно связаны, чем наблюдения, более отдаленные друг от друга. Кроме того, модели временных рядов часто используют естественный односторонний порядок времени, так что значения для данного периода будут выражены как вытекающие каким-то образом из прошлых значений, а не из будущих значений (см. обратимость времени ).
Анализ временных рядов может применяться к действительным , непрерывным данным, дискретным числовым данным или дискретным символьным данным (т. е. последовательностям символов, таким как буквы и слова на английском языке [1] ).
Методы анализа временных рядов можно разделить на два класса: методы частотной области и методы временной области . Первые включают спектральный анализ и вейвлет-анализ ; вторые включают автокорреляционный и кросс-корреляционный анализ. Во временной области корреляция и анализ могут быть выполнены в фильтроподобной манере с использованием масштабированной корреляции , тем самым уменьшая необходимость работы в частотной области.
Кроме того, методы анализа временных рядов можно разделить на параметрические и непараметрические . Параметрические подходы предполагают, что базовый стационарный стохастический процесс имеет определенную структуру, которую можно описать с помощью небольшого числа параметров (например, с помощью модели авторегрессии или скользящего среднего ). В этих подходах задача состоит в оценке параметров модели, описывающей стохастический процесс. Напротив, непараметрические подходы явно оценивают ковариацию или спектр процесса, не предполагая, что процесс имеет какую-либо определенную структуру.
Методы анализа временных рядов также можно разделить на линейные и нелинейные , а также одномерные и многомерные .
Временной ряд — это один из типов панельных данных . Панельные данные — это общий класс, многомерный набор данных, тогда как набор данных временного ряда — это одномерная панель (как и набор данных поперечного сечения ). Набор данных может обладать характеристиками как панельных данных, так и данных временного ряда. Один из способов узнать — спросить, что делает одну запись данных уникальной по сравнению с другими записями. Если ответ — поле данных времени, то это кандидат на набор данных временного ряда. Если для определения уникальной записи требуется поле данных времени и дополнительный идентификатор, не связанный со временем (например, студенческий билет, биржевой символ, код страны), то это кандидат на панельные данные. Если различие заключается в невременном идентификаторе, то набор данных является кандидатом на набор данных поперечного сечения.
Для временных рядов доступно несколько типов мотивации и анализа данных, которые подходят для разных целей.
В контексте статистики , эконометрики , количественных финансов , сейсмологии , метеорологии и геофизики основной целью анализа временных рядов является прогнозирование . В контексте обработки сигналов , техники управления и техники связи он используется для обнаружения сигналов. Другие приложения находятся в добыче данных , распознавании образов и машинном обучении , где анализ временных рядов может использоваться для кластеризации , [2] [3] классификации , [4] запроса по содержанию, [5] обнаружения аномалий , а также прогнозирования . [6]

Простой способ изучить регулярный временной ряд — вручную с помощью линейной диаграммы . На графике данных показаны случаи смерти от туберкулеза в Соединенных Штатах [7] вместе с годовым изменением и процентным изменением из года в год. Общее число смертей снижалось каждый год до середины 1980-х годов, после чего время от времени наблюдались увеличения, часто пропорционально — но не абсолютно — довольно большие.
Исследование корпоративных аналитиков данных выявило две проблемы исследовательского анализа временных рядов: обнаружение формы интересных закономерностей и нахождение объяснения этих закономерностей. [8] Визуальные инструменты, представляющие данные временных рядов в виде матриц тепловых карт, могут помочь преодолеть эти проблемы.
Другие методы включают в себя:
Подгонка кривой [11] [12] — это процесс построения кривой или математической функции , которая наилучшим образом соответствует ряду точек данных , [13] возможно, с ограничениями. [14] [15] Подгонка кривой может включать либо интерполяцию , [16] [17] , где требуется точное соответствие данным, либо сглаживание , [18] [19], при котором строится «гладкая» функция, которая приблизительно соответствует данным. Связанная тема — регрессионный анализ , [20] [21], который больше фокусируется на вопросах статистического вывода, таких как степень неопределенности, присутствующая в кривой, которая соответствует данным, наблюдаемым со случайными ошибками. Подогнанных кривых можно использовать в качестве вспомогательного средства для визуализации данных, [22] [23] для вывода значений функции, когда данные отсутствуют, [24] и для суммирования взаимосвязей между двумя или более переменными. [25] Экстраполяция относится к использованию подобранной кривой за пределами диапазона наблюдаемых данных [26] и подвержена некоторой степени неопределенности [27], поскольку она может отражать метод, используемый для построения кривой, в той же степени, в какой она отражает наблюдаемые данные.
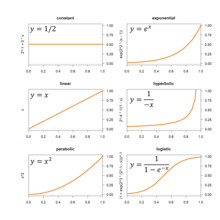
Для процессов, которые, как ожидается, будут в целом увеличиваться по величине, одну из кривых на графике (и многие другие) можно подогнать, оценив их параметры.
Построение экономических временных рядов включает оценку некоторых компонентов для некоторых дат путем интерполяции между значениями («эталонами») для более ранних и более поздних дат. Интерполяция — это оценка неизвестной величины между двумя известными величинами (историческими данными) или составление выводов об отсутствующей информации из имеющейся информации («чтение между строк»). [28] Интерполяция полезна, когда доступны данные, окружающие отсутствующие данные, и известны их тренд, сезонность и долгосрочные циклы. Это часто делается с использованием связанного ряда, известного для всех соответствующих дат. [29] В качестве альтернативы используется полиномиальная интерполяция или сплайн-интерполяция , когда кусочно- полиномиальные функции подгоняются во временные интервалы таким образом, что они плавно совпадают друг с другом. Другая проблема, которая тесно связана с интерполяцией, — это аппроксимация сложной функции простой функцией (также называемая регрессией ). Основное различие между регрессией и интерполяцией заключается в том, что полиномиальная регрессия дает один полином, который моделирует весь набор данных. Однако сплайн-интерполяция дает кусочно-непрерывную функцию, состоящую из множества полиномов, для моделирования набора данных.
Экстраполяция — это процесс оценки значения переменной за пределами исходного диапазона наблюдений на основе ее связи с другой переменной. Она похожа на интерполяцию , которая дает оценки между известными наблюдениями, но экстраполяция подвержена большей неопределенности и большему риску получения бессмысленных результатов.
В общем случае задача аппроксимации функции требует от нас выбора функции из хорошо определенного класса, которая близко соответствует («аппроксимирует») целевой функции в зависимости от задачи. Можно выделить два основных класса задач аппроксимации функции: во-первых, для известных целевых функций теория аппроксимации является разделом численного анализа , который исследует, как определенные известные функции (например, специальные функции ) могут быть аппроксимированы определенным классом функций (например, полиномами или рациональными функциями ), которые часто обладают желаемыми свойствами (недорогие вычисления, непрерывность, интегральные и предельные значения и т. д.).
Во-вторых, целевая функция, назовем ее g , может быть неизвестна; вместо явной формулы предоставляется только набор точек (временной ряд) вида ( x , g ( x )). В зависимости от структуры домена и кодомена g могут быть применимы несколько методов аппроксимации g . Например, если g является операцией над действительными числами , можно использовать методы интерполяции , экстраполяции , регрессионного анализа и подгонки кривой . Если кодомен (диапазон или целевой набор) g является конечным множеством, вместо этого мы имеем дело с проблемой классификации . Связанная проблема онлайн- аппроксимации временных рядов [30] заключается в суммировании данных за один проход и построении приближенного представления, которое может поддерживать различные запросы временных рядов с ограничениями на ошибку в худшем случае.
В некоторой степени различные проблемы ( регрессия , классификация , аппроксимация пригодности ) получили единую трактовку в статистической теории обучения , где они рассматриваются как проблемы контролируемого обучения .
В статистике прогнозирование является частью статистического вывода . Один из подходов к такому выводу известен как прогнозирующий вывод , но прогнозирование может быть выполнено в рамках любого из нескольких подходов к статистическому выводу. Действительно, одно из описаний статистики заключается в том, что она предоставляет средства передачи знаний о выборке населения всей популяции и другим связанным популяциям, что не обязательно то же самое, что прогнозирование с течением времени. Когда информация передается во времени, часто в определенные моменты времени, этот процесс известен как прогнозирование .
Отнесение шаблона временного ряда к определенной категории, например, определение слова на основе серии движений рук в языке жестов .
Этот подход основан на гармоническом анализе и фильтрации сигналов в частотной области с использованием преобразования Фурье и оценки спектральной плотности , развитие которой было значительно ускорено во время Второй мировой войны математиком Норбертом Винером , инженерами-электриками Рудольфом Э. Кальманом , Деннисом Габором и другими для фильтрации сигналов от шума и прогнозирования значений сигнала в определенный момент времени. См. Фильтр Калмана , Теория оценки и Цифровая обработка сигналов
Разделение временного ряда на последовательность сегментов. Часто бывает так, что временной ряд можно представить как последовательность отдельных сегментов, каждый из которых имеет свои собственные характерные свойства. Например, аудиосигнал от конференц-звонка можно разбить на части, соответствующие времени, в течение которого говорил каждый человек. При сегментации временного ряда цель состоит в том, чтобы определить граничные точки сегмента во временном ряду и охарактеризовать динамические свойства, связанные с каждым сегментом. Можно подойти к этой проблеме, используя обнаружение точек изменения или моделируя временной ряд как более сложную систему, такую как линейная система скачков Маркова.
Данные временных рядов могут быть сгруппированы, однако следует проявлять особую осторожность при рассмотрении кластеризации подпоследовательностей. [32] Кластеризация временных рядов может быть разделена на
Кластеризация временных рядов подпоследовательности привела к нестабильным (случайным) кластерам, вызванным извлечением признаков с использованием фрагментации со скользящими окнами. [33] Было обнаружено, что центры кластеров (среднее значение временного ряда в кластере - также временной ряд) следуют произвольно смещенному синусоидальному шаблону (независимо от набора данных, даже при реализациях случайного блуждания ). Это означает, что найденные центры кластеров не являются описательными для набора данных, поскольку центры кластеров всегда являются нерепрезентативными синусоидальными волнами.
Модели для данных временных рядов могут иметь множество форм и представлять различные стохастические процессы . При моделировании изменений на уровне процесса три широких класса, имеющих практическое значение, — это модели авторегрессии (AR), интегрированные (I) модели и модели скользящего среднего (MA). Эти три класса линейно зависят от предыдущих точек данных. [34] Комбинации этих идей создают модели авторегрессии скользящего среднего (ARMA) и авторегрессии интегрированного скользящего среднего (ARIMA). Модель авторегрессии дробно интегрированного скользящего среднего (ARFIMA) обобщает первые три. Расширения этих классов для работы с векторными данными доступны под заголовком многомерных моделей временных рядов, и иногда предшествующие аббревиатуры расширяются путем включения начальной «V» для «вектора», как в VAR для векторной авторегрессии . Дополнительный набор расширений этих моделей доступен для использования, когда наблюдаемый временной ряд управляется некоторым "вынуждающим" временным рядом (который может не иметь причинного эффекта на наблюдаемый ряд): отличие от многомерного случая заключается в том, что вынуждающий ряд может быть детерминированным или находиться под контролем экспериментатора. Для этих моделей аббревиатуры расширены с помощью конечного "X" для "экзогенного".
Нелинейная зависимость уровня ряда от предыдущих точек данных представляет интерес, отчасти из-за возможности создания хаотического временного ряда. Однако, что более важно, эмпирические исследования могут указать на преимущество использования прогнозов, полученных из нелинейных моделей, над прогнозами из линейных моделей, как, например, в нелинейных авторегрессионных экзогенных моделях . Дополнительные ссылки по нелинейному анализу временных рядов: (Kantz and Schreiber), [35] и (Abarbanel) [36]
Среди других типов нелинейных моделей временных рядов есть модели для представления изменений дисперсии с течением времени ( гетероскедастичность ). Эти модели представляют авторегрессионную условную гетероскедастичность (ARCH), и коллекция включает в себя широкий спектр представлений ( GARCH , TARCH, EGARCH, FIGARCH, CGARCH и т. д.). Здесь изменения в изменчивости связаны с недавними прошлыми значениями наблюдаемого ряда или предсказываются ими. Это контрастирует с другими возможными представлениями локально изменяющейся изменчивости, где изменчивость может быть смоделирована как обусловленная отдельным изменяющимся во времени процессом, как в дважды стохастической модели .
В недавних работах по анализам без моделей получили распространение методы, основанные на вейвлет-преобразовании (например, локально стационарные вейвлеты и нейронные сети, разложенные на вейвлеты). [37] Многомасштабные (часто называемые многоразрешающими) методы разлагают заданный временной ряд, пытаясь проиллюстрировать временную зависимость в нескольких масштабах. См. также методы мультифрактального переключения Маркова (MSMF) для моделирования эволюции волатильности.
Скрытая марковская модель (HMM) — это статистическая марковская модель, в которой предполагается, что моделируемая система является марковским процессом с ненаблюдаемыми (скрытыми) состояниями. HMM можно рассматривать как простейшую динамическую байесовскую сеть . Модели HMM широко используются в распознавании речи для перевода временного ряда произнесенных слов в текст.
Многие из этих моделей собраны в пакете Python sktime.
Для анализа временных рядов используется ряд различных обозначений. Общее обозначение, определяющее временной ряд X , который индексируется натуральными числами, записывается как
Другое распространенное обозначение —
где T — набор индексов .
Существует два набора условий, при которых строится большая часть теории:
Эргодичность подразумевает стационарность, но обратное не обязательно. Стационарность обычно классифицируется как строгая стационарность и стационарность в широком смысле или второго порядка . Как модели, так и приложения могут быть разработаны при каждом из этих условий, хотя модели в последнем случае можно считать лишь частично определенными.
Кроме того, анализ временных рядов может применяться там, где ряды сезонно стационарны или нестационарны. Ситуации, где амплитуды частотных компонентов изменяются со временем, могут рассматриваться в частотно-временном анализе , который использует частотно-временное представление временного ряда или сигнала. [38]
Инструменты для исследования данных временных рядов включают в себя:
Метрики или характеристики временных рядов , которые можно использовать для классификации временных рядов или регрессионного анализа : [41]
Временные ряды можно визуализировать с помощью двух категорий диаграмм: перекрывающиеся диаграммы и разделенные диаграммы. Перекрывающиеся диаграммы отображают все временные ряды на одном макете, тогда как разделенные диаграммы представляют их на разных макетах (но выровненных для сравнения) [45]
функции выполняются, если мы имеем хорошее или умеренное соответствие наблюдаемым данным.