Вязкоупругость

Свойства материалов, обладающих как вязкими, так и упругими характеристиками при деформации

В материаловедении и механике сплошных сред вязкоупругость — это свойство материалов , которые проявляют как вязкие , так и упругие характеристики при деформации . Вязкие материалы, такие как вода, сопротивляются сдвиговому потоку и линейно деформируются со временем при приложении напряжения . Эластичные материалы деформируются при растяжении и немедленно возвращаются в исходное состояние после снятия напряжения.

Вязкоупругие материалы обладают элементами обоих этих свойств и, как таковые, проявляют зависящую от времени деформацию. В то время как эластичность обычно является результатом растяжения связей вдоль кристаллографических плоскостей в упорядоченном твердом теле, вязкость является результатом диффузии атомов или молекул внутри аморфного материала. ^[1]

Фон

В девятнадцатом веке такие физики, как Джеймс Клерк Максвелл , Людвиг Больцман и лорд Кельвин , исследовали и экспериментировали с ползучестью и восстановлением стекол , металлов и резин . Вязкоупругость была дополнительно изучена в конце двадцатого века, когда были разработаны синтетические полимеры и использовались в различных приложениях. ^[2] Расчеты вязкоупругости сильно зависят от переменной вязкости , η . Обратная величина η также известна как текучесть , φ . Значение любой из них может быть получено как функция температуры или как заданное значение (например, для демпфера ). ^[1]

Различные типы реакций ( ) ${\displaystyle \sigma }$ на изменение скорости деформации ( ) ${\displaystyle d\varepsilon /dt}$

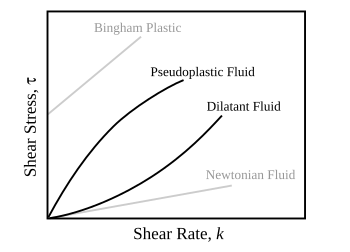
В зависимости от изменения скорости деформации в зависимости от напряжения внутри материала вязкость можно классифицировать как имеющую линейную, нелинейную или пластическую реакцию. Когда материал демонстрирует линейную реакцию, он классифицируется как ньютоновский материал . В этом случае напряжение линейно пропорционально скорости деформации. Если материал демонстрирует нелинейную реакцию на скорость деформации, он классифицируется как неньютоновская жидкость . Существует также интересный случай, когда вязкость уменьшается, поскольку скорость сдвига/деформации остается постоянной. Материал, который демонстрирует такой тип поведения, известен как тиксотропный . Кроме того, когда напряжение не зависит от этой скорости деформации, материал демонстрирует пластическую деформацию. ^[1] Многие вязкоупругие материалы демонстрируют поведение, подобное резине , которое объясняется термодинамической теорией полимерной эластичности.

Примерами вязкоупругих материалов являются аморфные полимеры, полукристаллические полимеры, биополимеры, металлы при очень высоких температурах и битумные материалы. Растрескивание происходит, когда деформация применяется быстро и за пределами предела упругости. Связки и сухожилия являются вязкоупругими, поэтому степень потенциального повреждения для них зависит как от скорости изменения их длины, так и от приложенной силы. ^{[ необходима цитата ]}

Вязкоупругий материал обладает следующими свойствами:

• Гистерезис виден на кривой напряжение-деформация
• происходит релаксация напряжения : ступенчатая постоянная деформация вызывает уменьшение напряжения
• происходит ползучесть : шаг постоянного напряжения вызывает увеличение деформации
• его жесткость зависит от скорости деформации ${\displaystyle {\dot {\varepsilon }}}$ или скорости напряжения ${\displaystyle {\dot {\sigma }}}$

Упругое и вязкоупругое поведение

Кривые напряжение-деформация для чисто упругого материала (a) и вязкоупругого материала (b). Красная область представляет собой петлю гистерезиса и показывает количество энергии, потерянной (в виде тепла) в цикле нагрузки и разгрузки. Она равна , где — напряжение, а — деформация. ^[1] ${\textstyle \oint \sigma \,d\varepsilon }$ ${\displaystyle \sigma }$ ${\displaystyle \varepsilon }$

В отличие от чисто упругих веществ, вязкоупругое вещество имеет упругий компонент и вязкий компонент. Вязкость вязкоупругого вещества придает веществу зависимость скорости деформации от времени. Чисто упругие материалы не рассеивают энергию (тепло), когда нагрузка прикладывается, а затем снимается. Однако вязкоупругое вещество рассеивает энергию, когда нагрузка прикладывается, а затем снимается. На кривой напряжение-деформация наблюдается гистерезис , при этом площадь петли равна энергии, потерянной во время цикла нагрузки. Поскольку вязкость является сопротивлением термически активированной пластической деформации, вязкий материал будет терять энергию в течение цикла нагрузки. Пластическая деформация приводит к потере энергии, что нехарактерно для реакции чисто упругого материала на цикл нагрузки. ^[1]

В частности, вязкоупругость — это молекулярная перестройка. Когда к вязкоупругому материалу, такому как полимер , прикладывается напряжение , части длинной полимерной цепи меняют положение. Это движение или перестройка называется ползучестью . Полимеры остаются твердым материалом, даже когда эти части их цепей перестраиваются, чтобы приспособиться к напряжению, и когда это происходит, в материале создается обратное напряжение. Когда обратное напряжение имеет ту же величину, что и приложенное напряжение, материал больше не ползет. Когда исходное напряжение снимается, накопленные обратные напряжения заставят полимер вернуться к своей первоначальной форме. Материал ползет, что дает префикс вязко-, и материал полностью восстанавливается, что дает суффикс -эластичность. ^[2]

Линейная вязкоупругость и нелинейная вязкоупругость

Линейная вязкоупругость имеет место, когда функция разделима как в реакции ползучести, так и в нагрузке. Все линейные вязкоупругие модели могут быть представлены уравнением Вольтерра, связывающим напряжение и деформацию : или где $${\displaystyle \varepsilon (t)={\frac {\sigma (t)}{E_{\text{inst,creep}}}}+\int _{0}^{t}K(t-t'){\dot {\sigma }}(t')dt'}$$ $${\displaystyle \sigma (t)=E_{\text{inst,relax}}\varepsilon (t)+\int _{0}^{t}F(t-t'){\dot {\varepsilon }}(t')dt'}$$

• t это время
• ${\displaystyle \sigma (t)}$это стресс
• ${\displaystyle \varepsilon (t)}$это напряжение
• ${\displaystyle E_{\text{inst,creep}}}$и являются мгновенными модулями упругости для ползучести и релаксации ${\displaystyle E_{\text{inst,relax}}}$
• K ( t ) —функция ползучести
• F ( t ) — функция релаксации

Линейная вязкоупругость обычно применима только для небольших деформаций .

Нелинейная вязкоупругость имеет место, когда функция неразделима. Обычно это происходит, когда деформации велики или если материал изменяет свои свойства при деформациях. Нелинейная вязкоупругость также объясняет наблюдаемые явления, такие как нормальные напряжения, истончение сдвига и утолщение растяжения в вязкоупругих жидкостях. ^[3]

Неэластичный материал является частным случаем вязкоупругого материала: неэластичный материал полностью восстанавливается до своего исходного состояния после снятия нагрузки .

При различении упругого, вязкого и вязкоупругого поведения полезно ссылаться на временную шкалу измерения относительно времени релаксации наблюдаемого материала, известную как число Деборы (De), где: ^[3] где $${\displaystyle De=\lambda /t}$$

• ${\displaystyle \lambda }$время релаксации материала
• ${\displaystyle t}$время пришло

Динамический модуль

Вязкоупругость изучается с помощью динамического механического анализа , прикладывая небольшое колебательное напряжение и измеряя результирующую деформацию.

• В чисто эластичных материалах напряжение и деформация совпадают по фазе, поэтому реакция одного на другое наступает немедленно.
• В чисто вязких материалах деформация отстает от напряжения на 90 градусов.
• Вязкоупругие материалы демонстрируют поведение, находящееся где-то посередине между этими двумя типами материалов, демонстрируя некоторое отставание в деформации.

Комплексный динамический модуль G можно использовать для представления соотношений между осциллирующим напряжением и деформацией: где ; — модуль накопления , а — модуль потерь , где и — амплитуды напряжения и деформации соответственно, а — фазовый сдвиг между ними. $${\displaystyle G=G'+iG''}$$ ${\displaystyle i^{2}=-1}$ ${\displaystyle G'}$ ${\displaystyle G''}$ $${\displaystyle G'={\frac {\sigma _{0}}{\varepsilon _{0}}}\cos \delta }$$ $${\displaystyle G''={\frac {\sigma _{0}}{\varepsilon _{0}}}\sin \delta }$$ ${\displaystyle \sigma _{0}}$ ${\displaystyle \varepsilon _{0}}$ ${\displaystyle \delta }$

Конститутивные модели линейной вязкоупругости

Сравнение ползучести и релаксации напряжений для трех- и четырехэлементных моделей

Вязкоупругие материалы, такие как аморфные полимеры, полукристаллические полимеры, биополимеры и даже живые ткани и клетки ^[4] , могут быть смоделированы для определения их напряжений и деформаций или силовых и смещенных взаимодействий, а также их временных зависимостей. Эти модели, которые включают модель Максвелла , модель Кельвина-Фойгта , стандартную линейную модель твердого тела и модель Бюргерса , используются для прогнозирования реакции материала при различных условиях нагрузки.

Вязкоупругое поведение имеет упругие и вязкие компоненты, смоделированные как линейные комбинации пружин и амортизаторов соответственно. Каждая модель отличается расположением этих элементов, и все эти вязкоупругие модели могут быть эквивалентно смоделированы как электрические цепи.

В эквивалентной электрической цепи напряжение представлено током, а скорость деформации — напряжением. Модуль упругости пружины аналогичен обратной величине индуктивности цепи (она накапливает энергию), а вязкость амортизатора — сопротивлению цепи (она рассеивает энергию).

Упругие компоненты, как упоминалось ранее, можно смоделировать как пружины с упругой постоянной E, учитывая формулу: где σ — напряжение, E — модуль упругости материала, а ε — деформация, возникающая при заданном напряжении, аналогично закону Гука . $${\displaystyle \sigma =E\varepsilon }$$

Вязкие компоненты можно смоделировать как амортизаторы, так что соотношение между напряжением и скоростью деформации можно задать следующим образом, где σ — напряжение, η — вязкость материала, а dε/dt — производная деформации по времени. $${\displaystyle \sigma =\eta {\frac {d\varepsilon }{dt}}}$$

Соотношение между напряжением и деформацией может быть упрощено для определенных скоростей напряжения или деформации. Для высоких скоростей напряжения или деформации/коротких периодов времени доминируют производные по времени компоненты соотношения напряжения и деформации. В этих условиях его можно аппроксимировать как жесткий стержень, способный выдерживать высокие нагрузки без деформации. Следовательно, демпфер можно считать «короткозамкнутым». ^{[5] [6]}

Наоборот, для состояний с низким напряжением/более длительных периодов времени компоненты производной по времени незначительны, и демпфер может быть эффективно удален из системы – «разомкнутая» цепь. ^[6] В результате, только пружина, подключенная параллельно демпферу, будет вносить вклад в общую деформацию в системе. ^[5]

модель Максвелла

модель Максвелла

Модель Максвелла может быть представлена ​​чисто вязким демпфером и чисто упругой пружиной, соединенными последовательно, как показано на схеме. Модель может быть представлена ​​следующим уравнением: $${\displaystyle \sigma +{\frac {\eta }{E}}{\dot {\sigma }}=\eta {\dot {\varepsilon }}}$$

Согласно этой модели, если материал подвергается постоянному напряжению, напряжения постепенно ослабевают . Когда материал подвергается постоянному напряжению, деформация имеет два компонента. Во-первых, упругий компонент возникает мгновенно, соответствующий пружине, и немедленно ослабевает после снятия напряжения. Второй — вязкий компонент, который растет со временем, пока прикладывается напряжение. Модель Максвелла предсказывает, что напряжение экспоненциально затухает со временем, что верно для большинства полимеров. Одним из ограничений этой модели является то, что она неточно предсказывает ползучесть. Модель Максвелла для условий ползучести или постоянного напряжения постулирует, что деформация будет линейно увеличиваться со временем. Однако полимеры в большинстве случаев показывают, что скорость деформации уменьшается со временем. ^[2]

Эту модель можно применять к мягким твердым телам: термопластичным полимерам при температуре, близкой к их температуре плавления, свежему бетону (без учета его старения) и многочисленным металлам при температуре, близкой к их температуре плавления.

Однако представленное здесь уравнение не имеет последовательного вывода из более микроскопической модели и не является независимым от наблюдателя. Верхнеконвективная модель Максвелла является его обоснованной формулировкой в ​​терминах тензора напряжений Коши и представляет собой простейшую тензорную конститутивную модель для вязкоупругости (см., например, ^[7] или ^[6] ).

Модель Кельвина–Фойгта

Схематическое изображение модели Кельвина–Фойгта

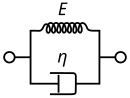
Модель Кельвина–Фойгта, также известная как модель Фойгта, состоит из ньютоновского демпфера и упругой пружины Гука, соединенных параллельно, как показано на рисунке. Она используется для объяснения поведения ползучести полимеров.

Определяющее соотношение выражается линейным дифференциальным уравнением первого порядка: $${\displaystyle \sigma =E\varepsilon +\eta {\dot {\varepsilon }}}$$

Эта модель представляет собой твердое тело, подвергающееся обратимой вязкоупругой деформации. При приложении постоянного напряжения материал деформируется с уменьшающейся скоростью, асимптотически приближаясь к стационарной деформации. Когда напряжение снимается, материал постепенно релаксирует до своего недеформированного состояния. При постоянном напряжении (ползучести) модель вполне реалистична, поскольку она предсказывает, что деформация стремится к σ/E по мере того, как время продолжается до бесконечности. Подобно модели Максвелла, модель Кельвина-Фойгта также имеет ограничения. Модель чрезвычайно хороша для моделирования ползучести материалов, но в отношении релаксации модель гораздо менее точна. ^[8]

Эту модель можно применять к органическим полимерам, резине и древесине, когда нагрузка не слишком высока.

Стандартная линейная твердотельная модель

Стандартная линейная модель твердого тела, также известная как модель Зенера, состоит из двух пружин и демпфера. Это самая простая модель, которая правильно описывает как поведение ползучести, так и релаксации напряжения вязкоупругого материала. Для этой модели определяющими определяющими соотношениями являются:

При постоянном напряжении моделируемый материал мгновенно деформируется до некоторой деформации, которая является мгновенной упругой частью деформации. После этого он продолжит деформироваться и асимптотически приблизится к стационарной деформации, которая является запаздывающей упругой частью деформации. Хотя стандартная линейная твердотельная модель точнее моделей Максвелла и Кельвина–Фойгта в прогнозировании реакций материала, математически она возвращает неточные результаты для деформации при определенных условиях нагрузки.

Модель Джеффриса

Модель Джеффриса, как и модель Зенера, является трехэлементной. Она состоит из двух демпферов и пружины. ^[9]

Модель Джеффриса

В 1929 году Гарольд Джеффрис предложил изучать мантию Земли . ^[10]

Модель бургеров

Модель Бюргерса состоит либо из двух компонентов Максвелла, соединенных параллельно, либо из компонента Кельвина–Фойгта, пружины и демпфера, соединенных последовательно. Для этой модели определяющими определяющими соотношениями являются:

Эта модель включает вязкое течение в стандартную линейную модель твердого тела, давая линейно возрастающую асимптоту для деформации в условиях фиксированной нагрузки.

Обобщенная модель Максвелла

Схема модели Максвелла-Вихерта

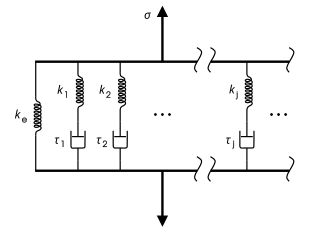
Обобщенная модель Максвелла, также известная как модель Вихерта, является наиболее общей формой линейной модели вязкоупругости. Она учитывает, что релаксация происходит не в один момент времени, а в распределении времен. Из-за молекулярных сегментов разной длины, причем более короткие вносят меньший вклад, чем более длинные, существует различное распределение времени. Модель Вихерта показывает это, имея столько пружинно-амортизационных элементов Максвелла, сколько необходимо для точного представления распределения. На рисунке справа показана обобщенная модель Вихерта. ^[11] Применения: металлы и сплавы при температурах ниже одной четверти их абсолютной температуры плавления (выраженной в К).

Конститутивные модели нелинейной вязкоупругости

Нелинейные вязкоупругие конститутивные уравнения необходимы для количественного учета явлений в жидкостях, таких как различия в нормальных напряжениях, истончение при сдвиге и утолщение при растяжении. ^[3] Обязательно, история, испытываемая материалом, необходима для учета поведения, зависящего от времени, и обычно включается в модели в качестве ядра истории K. ^[12 ]

Жидкость второго порядка

Жидкость второго порядка обычно считается простейшей нелинейной вязкоупругой моделью и обычно встречается в узкой области поведения материалов, возникающей при высоких амплитудах деформации и числе Дебора между ньютоновскими жидкостями и другими более сложными нелинейными вязкоупругими жидкостями. ^[3] Уравнение состояния жидкости второго порядка задается следующим образом:

$${\displaystyle \mathbf {T} =-p\mathbf {I} +2\eta _{0}\mathbf {D} -\psi _{1}\mathbf {D} ^{\triangledown }+4\psi _{2}\mathbf {D} \bullet \mathbf {D} }$$

где:

• ${\displaystyle \mathbf {I} }$является тензором идентичности
• ${\displaystyle \mathbf {D} }$это тензор деформации
• ${\displaystyle \eta _{0},\psi _{1},\psi _{2}}$обозначают вязкость, а также первый и второй коэффициенты нормального напряжения соответственно
• ${\displaystyle \mathbf {D} ^{\triangledown }}$обозначает верхнеконвективную производную тензора деформации, где и — материальная производная тензора деформации по времени. ^[3] $${\displaystyle \mathbf {D} ^{\triangledown }\equiv {\dot {\mathbf {D} }}-(\bigtriangledown \mathbf {v} )^{\mathbf {T} }\bullet \mathbf {D} -\mathbf {D} \bullet \bigtriangledown \mathbf {v} }$$ ${\displaystyle {\dot {\mathbf {D} }}\equiv {\frac {\partial }{\partial t}}\mathbf {D} +\mathbf {v} \bullet \bigtriangledown \mathbf {D} }$

Модель Максвелла с верхней конвекцией

Модель Максвелла с верхней конвекцией включает нелинейное поведение времени в вязкоупругую модель Максвелла, заданную следующим образом: ^[3]

$${\displaystyle \mathbf {\tau } +\lambda \mathbf {\tau } ^{\triangledown }=2\eta _{0}\mathbf {D} }$$где обозначает тензор напряжений. ${\displaystyle \mathbf {\tau } }$

Модель Oldroyd-B

Модель Oldroyd-B является расширением модели Upper Convected Maxwell и интерпретируется как растворитель, заполненный эластичными шариками и пружинными гантелями. Модель названа в честь ее создателя Джеймса Г. Олдройда . ^{[13] [14] [15]}

Модель можно записать как: где: $${\displaystyle \mathbf {T} +\lambda _{1}{\stackrel {\nabla }{\mathbf {T} }}=2\eta _{0}(\mathbf {D} +\lambda _{2}{\stackrel {\nabla }{\mathbf {D} }})}$$

• ${\displaystyle \mathbf {T} }$— тензор напряжений ;
• ${\displaystyle \lambda _{1}}$время релаксации;
• ${\displaystyle \lambda _{2}}$время замедления = ; ${\displaystyle {\frac {\eta _{s}}{\eta _{0}}}\lambda _{1}}$
• ${\displaystyle {\stackrel {\nabla }{\mathbf {T} }}}$— верхняя конвективная производная по времени тензора напряжений: $${\displaystyle {\stackrel {\nabla }{\mathbf {T} }}={\frac {\partial }{\partial t}}\mathbf {T} +\mathbf {v} \cdot \nabla \mathbf {T} -((\nabla \mathbf {v} )^{T}\cdot \mathbf {T} +\mathbf {T} \cdot (\nabla \mathbf {v} ));}$$
• ${\displaystyle \mathbf {v} }$скорость жидкости;
• ${\displaystyle \eta _{0}}$общая вязкость, состоящая из компонентов растворителя и полимера, ; ${\displaystyle \eta _{0}=\eta _{s}+\eta _{p}}$
• ${\displaystyle \mathbf {D} }$— тензор скорости деформации или тензор скорости деформации, . ${\displaystyle \mathbf {D} ={\frac {1}{2}}\left[{\boldsymbol {\nabla }}\mathbf {v} +({\boldsymbol {\nabla }}\mathbf {v} )^{T}\right]}$

Хотя модель дает хорошие приближения вязкоупругих жидкостей в сдвиговом потоке, она имеет нефизическую сингулярность в экстенсивном потоке, где гантели бесконечно растянуты. Это, однако, специфично для идеализированного потока; в случае геометрии крест-щели экстенсивный поток не идеален, поэтому напряжение, хотя и сингулярно, остается интегрируемым, хотя напряжение бесконечно в соответственно бесконечно малой области. ^[15]

Если вязкость растворителя равна нулю, модель Олдройда-Б становится верхней конвективной моделью Максвелла .

модель Вагнера

Модель Вагнера можно рассматривать как упрощенную практическую форму модели Бернстайна–Кирсли–Запаса. Модель была разработана немецким реологом Манфредом Вагнером .

Для изотермических условий модель можно записать в виде: $${\displaystyle \mathbf {\sigma } (t)=-p\mathbf {I} +\int _{-\infty }^{t}M(t-t')h(I_{1},I_{2})\mathbf {B} (t')\,dt'}$$

где:

• ${\displaystyle \mathbf {\sigma } (t)}$— тензор напряжений Коши как функция времени t ,
• p — давление
• ${\displaystyle \mathbf {I} }$это единичный тензор
• M — функция памяти, показывающая, обычно выражаемая в виде суммы экспоненциальных членов для каждого режима релаксации : где для каждого режима релаксации — модуль релаксации, а — время релаксации; $${\displaystyle M(x)=\sum _{k=1}^{m}{\frac {g_{i}}{\theta _{i}}}\exp \left({\frac {-x}{\theta _{i}}}\right),}$$ ${\displaystyle g_{i}}$ ${\displaystyle \theta _{i}}$
• ${\displaystyle h(I_{1},I_{2})}$— функция демпфирования деформации , зависящая от первого и второго инвариантов тензора Фингера . ${\displaystyle \mathbf {B} }$

Функцию деформационного упрочнения обычно записывают так: Если значение функции деформационного упрочнения равно единице, то деформация мала; если оно приближается к нулю, то деформации велики. ^{[16] [17]} $${\displaystyle h(I_{1},I_{2})=m^{*}\exp(-n_{1}{\sqrt {I_{1}-3}})+(1-m^{*})\exp(-n_{2}{\sqrt {I_{2}-3}})}$$

Серия Прони

В одномерном релаксационном тесте материал подвергается внезапной деформации, которая сохраняется постоянной в течение всего теста, а напряжение измеряется с течением времени. Начальное напряжение обусловлено упругой реакцией материала. Затем напряжение со временем ослабевает из-за вязких эффектов в материале. Обычно применяется либо растяжение, либо сжатие, либо объемное сжатие, либо сдвиговая деформация. Полученные данные о напряжении во времени можно подогнать под ряд уравнений, называемых моделями. Только обозначения меняются в зависимости от типа применяемой деформации: релаксация растяжения-сжатия обозначается , сдвиг обозначается , объем обозначается . Ряд Прони для релаксации сдвига имеет вид ${\displaystyle E}$ ${\displaystyle G}$ ${\displaystyle K}$

$${\displaystyle G(t)=G_{\infty }+\sum _{i=1}^{N}G_{i}\exp(-t/\tau _{i})}$$

где — долгосрочный модуль после того, как материал полностью расслабился, — времена релаксации (не путать с на диаграмме); чем выше их значения, тем больше времени требуется для релаксации напряжения. Данные подгоняются под уравнение с помощью алгоритма минимизации, который корректирует параметры ( ) для минимизации ошибки между прогнозируемыми и данными значениями. ^[18] ${\displaystyle G_{\infty }}$ ${\displaystyle \tau _{i}}$ ${\displaystyle \tau _{i}}$ ${\displaystyle G_{\infty },G_{i},\tau _{i}}$

Альтернативная форма получается, если учесть, что модуль упругости связан с долговременным модулем соотношением

$${\displaystyle G(t=0)=G_{0}=G_{\infty }+\sum _{i=1}^{N}G_{i}}$$

Поэтому,

$${\displaystyle G(t)=G_{0}-\sum _{i=1}^{N}G_{i}\left[1-e^{-t/\tau _{i}}\right]}$$

Эта форма удобна, когда модуль упругого сдвига получается из данных, независимых от данных релаксации, и/или для компьютерной реализации, когда желательно указать упругие свойства отдельно от вязких свойств, как в Simulia (2010). ^[19] ${\displaystyle G_{0}}$

Эксперимент по ползучести обычно проще выполнить, чем эксперимент по релаксации, поэтому большинство данных доступны в виде зависимости податливости (ползучести) от времени. ^[20] К сожалению, не существует известной замкнутой формы для податливости (ползучести) в терминах коэффициента ряда Прони. Поэтому, если у вас есть данные по ползучести, нелегко получить коэффициенты ряда Прони (релаксации), которые необходимы, например, в. ^[19] Целесообразный способ получения этих коэффициентов заключается в следующем. Во-первых, подгоните данные по ползучести к модели, которая имеет решения в замкнутой форме как по податливости, так и по релаксации; например, модель Максвелла-Кельвина (уравнение 7.18-7.19) в Barbero (2007) ^[21] или модель Standard Solid (уравнение 7.20-7.21) в Barbero (2007) ^[21] (раздел 7.1.3). После того, как параметры модели ползучести известны, создайте релаксационные псевдоданные с помощью сопряженной релаксационной модели для тех же времен исходных данных. Наконец, подгоните псевдоданные к рядам Прони.

Влияние температуры

Вторичные связи полимера постоянно разрываются и восстанавливаются из-за теплового движения. Приложение напряжения благоприятствует некоторым конформациям по сравнению с другими, поэтому молекулы полимера будут постепенно «перетекать» в предпочтительные конформации с течением времени. ^[22] Поскольку тепловое движение является одним из факторов, способствующих деформации полимеров, вязкоупругие свойства изменяются с повышением или понижением температуры. В большинстве случаев модуль ползучести, определяемый как отношение приложенного напряжения к зависящей от времени деформации, уменьшается с повышением температуры. Вообще говоря, повышение температуры коррелирует с логарифмическим уменьшением времени, необходимого для придания равной деформации при постоянном напряжении. Другими словами, требуется меньше работы, чтобы растянуть вязкоупругий материал на равное расстояние при более высокой температуре, чем при более низкой температуре.

Более подробное влияние температуры на вязкоупругое поведение полимера можно изобразить на графике, как показано на рисунке.

В типичные полимеры входят в основном пять областей (некоторые обозначаются как четыре, что объединяет IV и V вместе). ^[23]

• Область I: Стеклообразное состояние полимера представлено в этой области. Температура в этой области для данного полимера слишком низкая, чтобы обеспечить молекулярное движение. Следовательно, движение молекул заморожено в этой области. Механическое свойство твердое и хрупкое в этой области. ^[24]
• Область II: Полимер проходит температуру стеклования в этой области. За пределами Tg тепловой энергии, предоставляемой окружающей средой, достаточно, чтобы разморозить движение молекул. Молекулам разрешено иметь локальное движение в этой области, что приводит к резкому падению жесткости по сравнению с областью I.
• Область III: область резинового плато. Материалы, лежащие в этой области, будут существовать в дальнодействующей эластичности, обусловленной энтропией. Например, резиновая лента неупорядочена в исходном состоянии этой области. При растягивании резиновой ленты вы также выравниваете структуру, чтобы она была более упорядоченной. Поэтому при отпускании резиновой ленты она будет спонтанно стремиться к более высокому состоянию энтропии, следовательно, вернется в исходное состояние. Это то, что мы назвали восстановлением формы эластичности, обусловленной энтропией.
• Область IV: Поведение в области резиноподобного течения сильно зависит от времени. Полимеры в этой области должны использовать суперпозицию времени и температуры, чтобы получить более подробную информацию для осторожного решения о том, как использовать материалы. Например, если материал используется для решения задач с коротким временем взаимодействия, он может представлять собой «жесткий» материал. При использовании для задач с длительным временем взаимодействия он будет действовать как «мягкий» материал. ^[25]
• Область V: Вязкий полимер легко течет в этой области. Еще одно значительное падение жесткости.

Температурная зависимость модуля

Экстремально низкие температуры могут привести к тому, что вязкоупругие материалы перейдут в стеклообразное состояние и станут хрупкими . Например, воздействие экстремально низких температур ( сухой лед , замораживающий спрей и т. д.) на чувствительные к давлению клеи приводит к потере ими липкости, что приводит к отслоению.

Вязкоупругая ползучесть

а) Приложенное напряжение и б) вызванная деформация как функции времени в течение короткого периода для вязкоупругого материала.

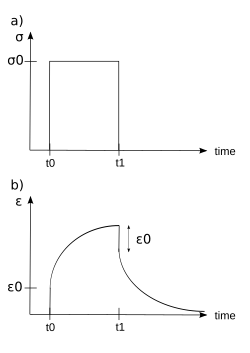
При воздействии ступенчатого постоянного напряжения вязкоупругие материалы испытывают зависящее от времени увеличение деформации. Это явление известно как вязкоупругая ползучесть.

В момент времени вязкоупругий материал нагружается постоянным напряжением, которое поддерживается в течение достаточно длительного периода времени. Материал реагирует на напряжение деформацией, которая увеличивается до тех пор, пока материал в конечном итоге не разрушится, если это вязкоупругая жидкость. Если же это вязкоупругое твердое тело, оно может разрушится или не разрушится в зависимости от приложенного напряжения по сравнению с предельным сопротивлением материала. Когда напряжение поддерживается в течение более короткого периода времени, материал испытывает начальную деформацию до момента времени , после чего деформация немедленно уменьшается (разрыв), а затем постепенно уменьшается временами до остаточной деформации. ${\displaystyle t_{0}}$ ${\displaystyle t_{1}}$ ${\displaystyle t>t_{1}}$

Данные о вязкоупругой ползучести можно представить, построив график модуля ползучести (постоянное приложенное напряжение, деленное на общую деформацию в определенное время) как функцию времени. ^[26] Ниже критического напряжения вязкоупругий модуль ползучести не зависит от приложенного напряжения. Семейство кривых, описывающих деформацию в зависимости от времени, ответ на различное приложенное напряжение, может быть представлено одной кривой вязкоупругого модуля ползучести в зависимости от времени, если приложенные напряжения ниже значения критического напряжения материала.

Вязкоупругая ползучесть важна при рассмотрении долгосрочного структурного проектирования. Учитывая условия нагрузки и температуры, проектировщики могут выбирать материалы, которые лучше всего подходят для срока службы компонентов.

Измерение

Реометрия сдвига

Сдвиговые реометры основаны на идее помещения измеряемого материала между двумя пластинами, одна или обе из которых движутся в направлении сдвига, чтобы вызвать напряжения и деформации в материале. Испытание может проводиться при постоянной скорости деформации, напряжении или колебательным образом (форма динамического механического анализа ). ^[27] Сдвиговые реометры обычно ограничены краевыми эффектами, когда материал может вытекать между двумя пластинами и проскальзывать на границе раздела материал/пластина.

Экстенсиональная реометрия

Реометры растяжения, также известные как экстензиометры, измеряют вязкоупругие свойства путем вытягивания вязкоупругой жидкости, как правило, одноосно. ^[28] Поскольку это обычно использует капиллярные силы и ограничивает жидкость узкой геометрией, этот метод часто ограничивается жидкостями с относительно низкой вязкостью, такими как разбавленные растворы полимеров или некоторые расплавленные полимеры. ^[28] Реометры растяжения также ограничены краевыми эффектами на концах экстензиометра и разницей давления внутри и снаружи капилляра. ^[3]

Несмотря на очевидные ограничения, упомянутые выше, реометрию растяжения можно также проводить на жидкостях с высокой вязкостью. Хотя для этого требуется использование различных инструментов, эти методы и аппараты позволяют изучать вязкоупругие свойства растяжения таких материалов, как расплавы полимеров. Три наиболее распространенных инструмента реометрии растяжения, разработанных за последние 50 лет, — это реометр Мейсснера, реометр растяжения нити (FiSER) и реометр растяжения Сентманата (SER).

Реометр типа Мейсснера, разработанный Мейсснером и Хостетлером в 1996 году, использует два набора вращающихся в противоположных направлениях роликов для одноосной деформации образца. ^[29] Этот метод использует постоянную длину образца на протяжении всего эксперимента и поддерживает образец между роликами с помощью воздушной подушки, чтобы исключить эффекты провисания образца. Он страдает от нескольких проблем — например, жидкость может проскальзывать на ремнях, что приводит к более низким скоростям деформации, чем можно было бы ожидать. Кроме того, это оборудование сложно в эксплуатации и дорого в приобретении и обслуживании.

Реометр FiSER просто содержит жидкость между двумя пластинами. Во время эксперимента верхняя пластина удерживается неподвижно, а к нижней пластине прикладывается сила, отодвигающая ее от верхней. ^[30] Скорость деформации измеряется скоростью изменения радиуса образца в его середине. Она рассчитывается с помощью следующего уравнения: где — значение среднего радиуса, а — скорость деформации. Затем вязкость образца рассчитывается с помощью следующего уравнения: где — вязкость образца, а — сила, приложенная к образцу для его разрыва. $${\displaystyle {\dot {\epsilon }}=-{\frac {2}{R}}{dR \over dt}}$$ ${\displaystyle R}$ ${\displaystyle {\dot {\epsilon }}}$ $${\displaystyle \eta ={\frac {F}{\pi R^{2}{\dot {\epsilon }}}}}$$ ${\displaystyle \eta }$ ${\displaystyle F}$

Подобно реометру типа Мейсснера, реометр SER использует набор из двух роликов для деформации образца с заданной скоростью. ^[31] Затем он вычисляет вязкость образца, используя хорошо известное уравнение: где — напряжение, — вязкость, — скорость деформации. Напряжение в этом случае определяется с помощью датчиков крутящего момента, имеющихся в приборе. Небольшой размер этого прибора упрощает его использование и исключает провисание образца между роликами. Схему, подробно описывающую работу экстенсионального реометра SER, можно найти справа. $${\displaystyle \sigma =\eta {\dot {\epsilon }}}$$ ${\displaystyle \sigma }$ ${\displaystyle \eta }$ ${\displaystyle {\dot {\epsilon }}}$

Схема реометра растяжения SER. Образец (коричневый) удерживается на двух цилиндрах (серых), которые затем вращаются в противоположных направлениях с различными скоростями деформации. Крутящий момент, необходимый для деформации образца с этими скоростями, рассчитывается с помощью набора датчиков крутящего момента, имеющихся в приборе. Затем эти значения крутящего момента преобразуются в значения напряжения, а напряжения и скорости деформации затем используются для определения вязкости образца.

Другие методы

Хотя существует множество инструментов, которые проверяют механический и вязкоупругий отклик материалов, широкополосная вязкоупругая спектроскопия (BVS) и резонансная ультразвуковая спектроскопия (RUS) чаще используются для проверки вязкоупругого поведения, поскольку их можно использовать выше и ниже температуры окружающей среды и они более специфичны для проверки вязкоупругости. Эти два инструмента используют механизм демпфирования на различных частотах и ​​временных диапазонах без обращения к суперпозиции времени и температуры . Использование BVS и RUS для изучения механических свойств материалов важно для понимания того, как будет вести себя материал, проявляющий вязкоупругость. ^[32]

Смотрите также

• пластик Бингама
• Биоматериал
• Биомеханика
• Вязкоупругость крови
• Эластичные жидкости с постоянной вязкостью
• Индекс деформации
• Стеклование
• Клей, чувствительный к давлению
• Реология
• Эластичность резины
• Глупая замазка
• Вязкоупругость кости
• Вязкопластичность
• Вязкоупругие струи

Ссылки

1. Мейерс и Чавла (1999): «Механическое поведение материалов», 98-103.
2. МакКрам, Бакли и Бакнелл (2003): «Принципы полимерной инженерии», 117-176.
3. Macosko, Christopher W. (1994). Реология: принципы, измерения и приложения. Нью-Йорк: VCH. ISBN 978-1-60119-575-3. OCLC  232602530.
4. Бисвас, Абхиджит; Маниваннан, М.; Шринивасан, Мандьям А. (2015). «Многомасштабная многослойная биомеханическая модель тельца Пачини». Труды IEEE по хаптике . 8 (1): 31–42. doi :10.1109/TOH.2014.2369416. PMID  25398182. S2CID  24658742.
5. Van Vliet, Krystyn J. (2006). "3.032 Механическое поведение материалов"
6. Cacopardo, Ludovica (январь 2019). «Инженерная вязкоупругость гидрогеля». Журнал механического поведения биомедицинских материалов . 89 : 162–167. doi : 10.1016/j.jmbbm.2018.09.031. hdl : 11568/930491 . PMID  30286375. S2CID  52918639 – через Elsevier. Ошибка цитирования: Именованная ссылка «:0» была определена несколько раз с различным содержанием (см. страницу справки ).
7. Ларсон, Рональд Г. (28 января 1999 г.). Структура и реология сложных жидкостей (темы химической инженерии): Ларсон, Рональд Г.: 9780195121971: Amazon.com: Книги . Oup USA. ISBN 019512197X.
8. Таннер, Роджер И. (1988). Инженерная реология . Oxford University Press. стр. 27. ISBN 0-19-856197-0.
9. Барнс, Говард А.; Хаттон, Джон Флетчер; Уолтерс, К. (1989). Введение в реологию. Elsevier. ISBN 978-0-444-87140-4.
10. Берд, Р. Байрон (1987-05-27). Динамика полимерных жидкостей, том 1: Механика жидкости. Wiley. ISBN 978-0-471-80245-7.
11. Ройланс, Дэвид (2001); «Инженерная вязкоупругость», 14–15
12. Драпака, CS; Сивалоганатан, S.; Тенти, G. (2007-10-01). «Нелинейные конститутивные законы в вязкоупругости». Математика и механика твердого тела . 12 (5): 475–501. doi :10.1177/1081286506062450. ISSN  1081-2865. S2CID  121260529.
13. Oldroyd, James (февраль 1950 г.). «О формулировке реологических уравнений состояния». Труды Лондонского королевского общества. Серия A, Математические и физические науки . 200 (1063): 523–541. Bibcode : 1950RSPSA.200..523O. doi : 10.1098/rspa.1950.0035. S2CID  123239889.
14. Оуэнс, RG; Филлипс, TN (2002). Вычислительная реология . Imperial College Press. ISBN 978-1-86094-186-3.
15. Poole, Rob (октябрь 2007 г.). "Чисто упругие асимметрии потока". Physical Review Letters . 99 (16): 164503. Bibcode :2007PhRvL..99p4503P. doi :10.1103/PhysRevLett.99.164503. hdl : 10400.6/634 . PMID  17995258.
16. Вагнер, Манфред (1976). «Анализ данных о нелинейном росте напряжения, зависящем от времени, для сдвигового и продольного течения расплава разветвленного полиэтилена низкой плотности». Rheologica Acta . 15 (2): 136–142. Bibcode : 1976AcRhe..15..136W. doi : 10.1007/BF01517505. S2CID  96165087.
17. Вагнер, Манфред (1977). «Прогнозирование разницы первичного нормального напряжения по данным сдвиговой вязкости с использованием одного интегрального уравнения состояния». Rheologica Acta . 16 (1977): 43–50. Bibcode : 1977AcRhe..16...43W. doi : 10.1007/BF01516928. S2CID  98599256.
18. EJ Barbero. «Принцип суперпозиции времени-температуры-возраста для прогнозирования долгосрочного отклика линейных вязкоупругих материалов», глава 2 в книге «Ползучесть и усталость в композитах с полимерной матрицей». Woodhead, 2011.
19. Simulia. Руководство пользователя Abaqus Analysis , 19.7.1 "Временная викоупругость", издание 6.10, 2010 г.
20. Компьютерный предварительный выбор материалов по единым стандартам
21. EJ Barbero. Конечно-элементный анализ композитных материалов. CRC Press, Бока-Ратон, Флорида, 2007.
22. SA Baeurle, A. Hotta, AA Гусев, Polymer 47 , 6243-6253 (2006).
23. Aklonis., JJ (1981). "Механические свойства полимеров". J Chem Educ . 58 (11): 892. Bibcode :1981JChEd..58..892A. doi :10.1021/ed058p892.
24. IM, Kalogeras (2012). «Природа стеклообразного состояния: структура и стеклование». Журнал материаловедения . 34 (3): 69.
25. Эмри, И. (2010). Зависимое от времени поведение твердых полимеров .
26. Розато и др. (2001): «Справочник по проектированию пластмасс», 63–64.
27. Magnin, A.; Piau, JM (1987-01-01). "Сдвиговая реометрия жидкостей с пределом текучести". Журнал неньютоновской механики жидкостей . 23 : 91–106. Bibcode :1987JNNFM..23...91M. doi :10.1016/0377-0257(87)80012-5. ISSN  0377-0257.
28. Dealy, JM (1978-01-01). "Extensional Rheometers for molten polymers; a review". Journal of Non-Newtonian Fluid Mechanics . 4 (1–2): 9–21. Bibcode :1978JNNFM...4....9D. doi :10.1016/0377-0257(78)85003-4. ISSN  0377-0257.
29. Мейсснер, Дж.; Хостеттлер, Дж. (1994-01-01). "Новый удлиняющий реометр для расплавов полимеров и других высоковязкоупругих жидкостей". Rheologica Acta . 33 (1): 1–21. Bibcode : 1994AcRhe..33....1M. doi : 10.1007/BF00453459. ISSN  1435-1528. S2CID  93395453.
30. Бах, Андерс; Расмуссен, Хенрик Коблиц; Хассагер, Оле (март 2003 г.). «Вязкость при растяжении для расплавов полимеров, измеренная в реометре для растяжения нитей». Журнал реологии . 47 (2): 429–441. Bibcode : 2003JRheo..47..429B. doi : 10.1122/1.1545072. ISSN  0148-6055. S2CID  44889615.
31. Сентманат, Мартин Л. (2004-12-01). «Миниатюрная универсальная испытательная платформа: от реологии расплава растяжения до поведения деформации твердого тела». Rheologica Acta . 43 (6): 657–669. Bibcode : 2004AcRhe..43..657S. doi : 10.1007/s00397-004-0405-4. ISSN  1435-1528. S2CID  73671672.
32. Род Лейкс (1998). Вязкоупругие твердые тела . CRC Press. ISBN 0-8493-9658-1.

• Силби и Альберти (2001): Физическая химия , 857. John Wiley & Sons, Inc.
• Алан С. Уайнман и К. Р. Раджагопал (2000): Механическая реакция полимеров: Введение
• Аллен и Томас (1999): Структура материалов , 51.
• Крэндал и др. (1999): Введение в механику твердого тела 348
• Ж. Лемэтр и Ж. Л. Шабош (1994) Механика твердых материалов
• Ю. Димитриенко (2011) Нелинейная механика сплошных сред и большие неупругие деформации , Springer, 772 стр.