Геометрическая серия

Сумма (бесконечной) геометрической прогрессии

Геометрический ряд 1/4 + 1/16 + 1/64 + 1/256 + ... показан в виде площадей фиолетовых квадратов. Каждый из фиолетовых квадратов имеет 1/4 площади следующего большего квадрата (1/2× 1/2 = 1/4, 1/4×1/4 = 1/16 и т. д.). Сумма площадей фиолетовых квадратов составляет одну треть площади большого квадрата.

Другой геометрический ряд (коэффициент a = 4/9 и общее отношение r = 1/9) показан в виде площадей фиолетовых квадратов. Общая площадь фиолетового цвета равна S = a /(1 – r ) = (4/9)/(1 – (1/9)) = 1/2, что можно подтвердить, заметив, что единичный квадрат разбит на бесконечное число количество L-образных областей, каждая из которых состоит из четырех фиолетовых квадратов и четырех желтых квадратов, которые наполовину фиолетовые.

В математике геометрическая прогрессия — это сумма бесконечного числа членов , имеющих постоянное соотношение между последовательными членами. Например, сериал

${\displaystyle {\frac {1}{2}}\,+\,{\frac {1}{4}}\,+\,{\frac {1}{8}}\,+\,{\frac {1}{16}}\,+\,\cdots }$

является геометрическим, поскольку каждый последующий член можно получить умножением предыдущего члена на . В общем случае геометрический ряд записывается как , где – коэффициент каждого члена, а – общее отношение между соседними членами. Геометрические ряды сыграли важную роль на раннем этапе развития исчисления , используются во всей математике и могут служить введением в часто используемые математические инструменты, такие как ряд Тейлора , ряд Фурье и матричная экспонента . ${\displaystyle 1/2}$ ${\displaystyle a+ar+ar^{2}+ar^{3}+...}$ ${\displaystyle a}$ ${\displaystyle r}$

Геометрическая серия имени указывает, что каждый термин представляет собой среднее геометрическое двух соседних с ним терминов, аналогично тому, как арифметическая серия имени указывает, что каждый термин является средним арифметическим двух соседних терминов.

Компоненты

Коэффициент а

Первые семь членов геометрической прогрессии 1 + r + r ² + r ³ ... нарисованы как функции в диапазоне | р | < 1. Замкнутая форма геометрической серии 1/(1 - r ) представляет собой черную пунктирную линию.

Геометрический ряд a + ar + ar ² + ar ³ + ... записывается в развернутом виде. ^[1] Все коэффициенты в геометрической прогрессии одинаковы. Напротив, степенной ряд , записанный как a ₀ + a ₁ r + a ₂ r ² + a ₃ r ³ + ... в развернутом виде, имеет коэффициенты a _i , которые могут меняться от члена к члену. Другими словами, геометрический ряд является частным случаем степенного ряда. Первый член геометрической прогрессии в развернутом виде — это коэффициент а этой геометрической прогрессии.

Помимо развернутой формы геометрической прогрессии, существует образующая форма ^[1] геометрической прогрессии, записываемая как

${\displaystyle \sum _{k=0}^{\infty }ar^{k}}$

и замкнутая форма геометрической прогрессии, записанная как

${\displaystyle {\frac {a}{1-r}}{\text{ for }}|r|<1.}$

Вывод закрытой формы из расширенной формы показан в разделе § Сумма этой статьи. Однако даже без этого вывода результат можно подтвердить делением в столбики : деление на (1 - r ) дает a + ar + ar ² + ar ³ + ... , что является расширенной формой геометрической прогрессии.

Часто в обозначениях удобно положить ряд равным сумме s и работать с геометрическим рядом

s = a + ar + ar ² + ar ³ + ar ⁴ + ... в нормированной форме

s / a = 1 + r + r ² + r ³ + r ⁴ + ... или в его нормализованной векторной форме

s / a = [1 1 1 1 1 ...][1 r r ² r ³ r ⁴ ...] ^T или в форме нормализованного частного ряда

s _n / a = 1 + r + r ² + r ³ + r ⁴ + ... + r ⁿ , где n — степень (или степень) последнего члена, входящего в частичную сумму s _n .

Изменение хотя бы одного из коэффициентов на нечто иное, чем коэффициент a , изменит результирующую сумму функций на некоторую функцию, отличную от a / (1 − r ), в пределах диапазона | р | < 1. Кроме того, особенно полезное изменение коэффициентов определяется рядом Тейлора , который описывает, как изменить коэффициенты так, чтобы сумма функций сходилась к любой выбранной пользователем достаточно гладкой функции в пределах диапазона.

Общее соотношение r

Сходимость геометрической прогрессии при r =1/2 и a =1/2

Сходимость геометрической прогрессии при r =1/2 и a =1

Крупный план накопленной суммы функций в диапазоне -1 < r < -0,5 при добавлении первых 11 членов геометрической прогрессии 1 + r + r ² + r ^{3 + ....} Геометрическая серия 1/(1 - r ) представляет собой красную пунктирную линию.

Сложный геометрический ряд (коэффициент a = 1 и общий коэффициент r = 0,5 e ^{iω ₀ t} ), сходящийся к окружности. В анимации каждый член геометрической прогрессии рисуется как вектор дважды : один раз в начале координат и второй раз в сумме векторов от начала до конца, которая сходится к кругу. Окружность пересекает действительную ось в точке 2 (= 1/(1-1/2), когда θ = 0) и в точке 2/3 (= 1/(1-(-1/2)) когда θ = 180 градусов).

Геометрический ряд a + ar + ar ² + ar ³ + ... представляет собой бесконечный ряд, определяемый всего двумя параметрами : коэффициентом a и общим отношением r . Общее отношение r — это отношение любого члена к предыдущему члену ряда. Или, что то же самое, общее отношение r — это множитель термина, используемый для вычисления следующего члена в ряду. В следующей таблице показаны несколько геометрических рядов:

Сходимость геометрического ряда зависит от значения общего отношения r :

• Если | р | < 1, члены ряда в пределе стремятся к нулю (становясь все меньшими по величине ), и ряд сходится к сумме a /(1 — r ).
• Если | р | = 1, ряд не сходится. Когда r = 1, все члены ряда одинаковы и ряд бесконечен. Когда r = −1, члены попеременно принимают два значения (например, 2, −2, 2, −2, 2,...). Сумма членов колеблется между двумя значениями (например, 2, 0, 2, 0, 2,...). Это другой тип расхождения. См., например , ряд Гранди : 1 - 1 + 1 - 1 + ···.
• Если | р | > 1 члены ряда становятся все больше и больше по величине. Сумма слагаемых также становится все больше и больше, и ряд не сходится к сумме. (Ряд расходится .)

Скорость сходимости также зависит от значения общего отношения r . В частности, скорость сходимости замедляется, когда r приближается к 1 или -1. Например, геометрическая прогрессия с a = 1 равна 1 + r + r ² + r ³ + ... и сходится к 1/(1 - r ), когда | р | < 1. Однако количество членов, необходимых для сходимости, приближается к бесконечности по мере того, как r приближается к 1, потому что a / (1 - r ) приближается к бесконечности, и каждый член ряда меньше или равен единице. Напротив, когда r приближается к −1, сумма первых нескольких членов геометрической прогрессии начинает сходиться к 1/2, но слегка меняется вверх или вниз в зависимости от того, имеет ли последний добавленный член четную или нечетную степень r . . Такое переворачивание вблизи r = −1 иллюстрируется на соседнем изображении, показывающем первые 11 членов геометрической прогрессии с a = 1 и | р | < 1.

Общее отношение r и коэффициент a также определяют геометрическую прогрессию , которая представляет собой список членов геометрической прогрессии, но без дополнений. Следовательно, геометрическая прогрессия a + ar + ar ² + ar ³ + ... имеет геометрическую прогрессию (также называемую геометрической последовательностью) a , ar , ar ² , ar ³ , ... Геометрическая прогрессия - настолько проста, насколько она проста. - моделирует удивительное количество природных явлений ,

• из некоторых крупнейших наблюдений, таких как расширение Вселенной , где общее отношение r определяется постоянной Хаббла ,
• до некоторых из мельчайших наблюдений, таких как распад радиоактивных атомов углерода-14, где общее соотношение r определяется периодом полураспада углерода-14 .

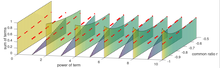
Кроме того, общее отношение r может быть комплексным числом, например | р |е ^{я θ} где | р | — величина вектора (или длина), θ — угол (или ориентация) вектора в комплексной плоскости , а i ² = -1. С общим соотношением | r |e ^{i θ} расширенная форма геометрической прогрессии равна a + a | р |е ^{я θ} + а | р | ² е ^{я2 θ} + а | р | ³ e ^{i3 θ} + ... Моделируя угол θ как линейно увеличивающийся во времени со скоростью некоторой угловой частоты ω ₀ (другими словами, делая замену θ = ω ₀ t ), расширенная форма геометрической прогрессии становится + а | р |е ^{я ω ₀ т} + а | р | ² е ^{я2 ω ₀ т} + а | р | ³ e ^{i3 ω ₀ t} + ... , где первый член — вектор длины a, вообще не вращающийся, а все остальные члены — векторы разной длины, вращающиеся на гармониках основной угловой частоты ω ₀ . Ограничение | r |<1 достаточно, чтобы координировать это бесконечное количество векторов разной длины, вращающихся с разной скоростью и описывающих круг, как показано в соседнем видео. Подобно тому, как ряд Тейлора описывает, как изменять коэффициенты, чтобы ряд сходился к выбранной пользователем достаточно гладкой функции в пределах диапазона, ряд Фурье описывает, как изменять коэффициенты (которые также могут быть комплексными числами, чтобы указать начальные углы). векторов), поэтому ряд сходится к выбранной пользователем периодической функции .

Сумма

В качестве альтернативы алгебраическому выводу формулы замкнутой формы геометрического ряда существует также следующий геометрический вывод. (ВЕРХ) Представьте первые n+1 членов s / a как области перекрывающихся подобных треугольников. ^[2] Например, площадь самого большого перекрывающегося (красного) треугольника равна bh /2 = (2)(1)/2 = 1, что является значением первого члена геометрической прогрессии. Площадь второго по величине перекрывающегося (зеленого) треугольника равна bh /2 = (2 r ^1/2 )( r ^1/2 )/2 = r , что является значением второго члена геометрической прогрессии. У каждого постепенно уменьшающегося треугольника основание и высота уменьшаются еще на один коэффициент r ^1/2 , в результате чего образуется последовательность площадей треугольника 1, r , r ² , r ³ , ... которая равна последовательности членов в нормированный геометрический ряд. (СРЕДНИЙ) В порядке от наибольшего к наименьшему удалите перекрывающуюся область каждого треугольника, которая всегда составляет часть r его площади, и масштабируйте оставшиеся 1− r неперекрывающейся площади треугольника на 1/(1− r ), так что площадь бывшего перекрывающегося треугольника, а теперь площадь неперекрывающейся трапеции, остается прежней. (ВНИЗУ) Объедините полученные n+1 непересекающиеся трапеции в одну неперекрывающуюся трапецию и вычислите ее площадь. Площадь этой агрегированной трапеции представляет собой значение частичного ряда. Эта площадь равна самому внешнему треугольнику за вычетом пустой вершины треугольника: s _n / a = (1− r ⁿ⁺¹ ) / (1 − r ), что упрощается до s / a = 1/(1− r ), когда n приближается к бесконечности и | р | < 1.

Сумма первых n членов геометрической прогрессии, до члена r ^n-1 включительно , определяется формулой в замкнутой форме:

$${\displaystyle {\begin{aligned}s_{n}&=ar^{0}+ar^{1}+\cdots +ar^{n-1}\\&=\sum _{k=0}^{n-1}ar^{k}=\sum _{k=1}^{n}ar^{k-1}\\&={\begin{cases}a\left({\frac {1-r^{n}}{1-r}}\right)&r\neq 1\\an&{\text{otherwise}}\end{cases}}\end{aligned}}}$$

где r — обычное отношение. Эту формулу в замкнутой форме для частичной суммы s _n можно получить , вычитая множество самоподобных членов следующим образом: ^{[3] [4] [5]}

$${\displaystyle {\begin{aligned}s_{n}&=ar^{0}+ar^{1}+\cdots +ar^{n-1},\\rs_{n}&=ar^{1}+ar^{2}+\cdots +ar^{n},\\s_{n}-rs_{n}&=ar^{0}-ar^{n},\\s_{n}\left(1-r\right)&=a\left(1-r^{n}\right),\\s_{n}&=a\left({\frac {1-r^{n}}{1-r}}\right),{\text{ for }}r\neq 1.\end{aligned}}}$$

Поскольку n приближается к бесконечности, абсолютное значение r должно быть меньше единицы, чтобы ряд сходился. Тогда сумма станет

$${\displaystyle {\begin{aligned}s&=a+ar+ar^{2}+ar^{3}+ar^{4}+\cdots \\&=\sum _{k=0}^{\infty }ar^{k}=\sum _{k=1}^{\infty }ar^{k-1}\\&={\frac {a}{1-r}},{\text{ for }}|r|<1.\end{aligned}}}$$

Формула также справедлива для комплексного r с соответствующим ограничением, согласно которому модуль r строго меньше единицы.

Кроме того, вопрос о том, сходится ли бесконечный ряд, по сути, является вопросом о расстоянии между двумя значениями: при достаточном количестве членов становится ли значение частичной суммы сколь угодно близким к конечному значению, к которому оно приближается? В приведенном выше выводе замкнутой формы геометрической прогрессии интерпретация расстояния между двумя значениями — это расстояние между их положениями на числовой прямой . Это наиболее распространенная интерпретация расстояния между двумя значениями. Однако p-адическая метрика , ставшая критическим понятием в современной теории чисел , предлагает такое определение расстояния, что геометрическая прогрессия 1 + 2 + 4 + 8 + ... с a = 1 и r = 2 действительно сходятся к a / (1 - r ) = 1 / (1 - 2) = -1, хотя r находится за пределами типичного диапазона сходимости | р | < 1.

Доказательство конвергенции

Мы можем доказать, что геометрическая прогрессия сходится , используя формулу суммы для геометрической прогрессии :

$${\displaystyle {\begin{aligned}1+r+r^{2}+r^{3}+\cdots \ &=\lim _{n\to \infty }\left(1+r+r^{2}+\cdots +r^{n}\right)\\&=\lim _{n\to \infty }{\frac {1-r^{n+1}}{1-r}}.\end{aligned}}}$$

${\displaystyle |r|<1,}$ ${\displaystyle r^{n+1}\to 0}$ ${\displaystyle n\to \infty }$

$${\displaystyle {\begin{aligned}\left(1+r+r^{2}+\cdots +r^{n}\right)(1-r)&=\left((1-r)+(r-r^{2})+(r^{2}-r^{3})+\dots +(r^{n}-r^{n+1})\right)\\&=1+(-r+r)+(-r^{2}+r^{2})+\dots +(-r^{n}+r^{n})-r^{n+1}\\&=1-r^{n+1}.\end{aligned}}}$$

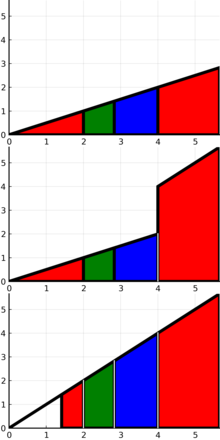
Альтернативно, геометрическая интерпретация сходимости показана на соседней диаграмме. Площадь белого треугольника — это остаток ряда = s − s _n = ar ^{n +1} / (1 − r ). Каждый дополнительный член частичного ряда уменьшает площадь остатка белого треугольника на площадь трапеции, представляющей добавленный член. Области трапеции (т. е. значения членов) становятся все тоньше, короче и ближе к началу координат. В пределе, когда число трапеций приближается к бесконечности, остаток белого треугольника исчезает, поскольку он заполнен трапециями, и, следовательно, s _n сходится к s , при условии | р |<1. Напротив, если | r |>1, области трапеций, представляющие члены ряда, вместо этого становятся все шире, выше и дальше от начала координат, не сходясь к началу координат и не сходясь как ряд.

Скорость сходимости

Сходящиеся чередующиеся геометрические ряды с общим соотношением r = -1/2 и коэффициентом a = 1. (ВЕРХ) Чередование положительных и отрицательных областей. (СРЕДНИЙ) Пробелы, вызванные добавлением смежных областей. (ВНИЗУ) Промежутки заполнены расширением и уменьшением высоты отдельных трапеций.

Зная, что ряд сходится, есть некоторые приложения, в которых также важно знать, насколько быстро он сходится. Для геометрического ряда одним из удобных показателей скорости сходимости является то, насколько уменьшается остаток предыдущего ряда из-за последнего члена частичного ряда. Учитывая, что последний член равен ar ⁿ , а остаток предыдущего ряда равен s - s _n-1 = ar ⁿ / (1 - r )), эта мера скорости сходимости геометрического ряда равна ar ⁿ / ( ar ⁿ / ( 1 - r )) = 1 - r , если 0 ≤ r < 1.

Если r < 0, соседние члены геометрической прогрессии попеременно могут быть положительными и отрицательными. Геометрическая интерпретация сходящегося знакопеременного геометрического ряда показана на соседней диаграмме, на которой под осью x показаны области отрицательных членов. Сопряжение и суммирование каждой положительной области с ее отрицательным соседом меньшей площади приводит к получению неперекрывающихся трапеций, разделенных промежутками. Чтобы удалить пробелы, расширите каждую трапецию, чтобы покрыть крайнюю правую часть 1 - r ² исходной области треугольника, а не только самую правую 1 - | р |. Однако для сохранения тех же площадей трапеций во время этого расширяющего преобразования необходимо масштабирование: масштаб*(1 - r ² ) = (1 - | r |) или масштаб = (1 - | r |) / (1 - r ² ) = (1 + r ) / (1 - r ² ) = (1 + r ) / ((1 + r )(1 - r )) = 1 / (1 - r ), где -1 < r ≤ 0. Примечание. что, поскольку r <0, этот масштаб уменьшает амплитуду разделенных трапеций, чтобы заполнить пробелы в разделении. Напротив, для случая r > 0 тот же масштаб 1/(1 - r ) увеличивает амплитуду неперекрывающихся трапеций, чтобы учесть потерю перекрывающихся областей.

После удаления пробелов пары членов в сходящейся знакопеременной геометрической прогрессии становятся сходящейся (нечередующейся) геометрической последовательностью с общим отношением r ² для учета спаривания членов, коэффициентом a = 1/(1 - r ) для учета заполнение пробела и степень (т. е. член наивысшей степени) частичного ряда, названного m вместо n, чтобы подчеркнуть, что члены были парными. Как и в случае r > 0, скорость сходимости r < 0 = ar ^2m / ( s - s _m-1 ) = 1 - r ² , что совпадает со скоростью сходимости неперемежающейся геометрической прогрессии, если ее члены были в одинаковой паре. Следовательно, скорость сходимости не зависит от n или m и, что, возможно, более удивительно, не зависит от знака общего отношения. Одна из точек зрения, которая помогает объяснить переменную скорость сходимости, симметричную относительно r = 0, заключается в том, что каждый добавленный член частичного ряда вносит конечный вклад в бесконечную сумму при r = 1, а каждый добавленный член частичного ряда вносит конечный вклад. к бесконечному наклону при r = -1.

Вывод

Доказательство без слов формулы суммы геометрической прогрессии – если | р | < 1 и n → ∞, член r ⁿ обращается в нуль, оставляя S _∞ =а/1 - р

Конечная серия

Чтобы вывести эту формулу, сначала напишите общую геометрическую прогрессию в виде:

$${\displaystyle \sum _{k=1}^{n}ar^{k-1}=ar^{0}+ar^{1}+ar^{2}+ar^{3}+\cdots +ar^{n-1}.}$$

Мы можем найти более простую формулу для этой суммы, умножив обе части приведенного выше уравнения на 1 - r , и мы увидим, что

$${\displaystyle {\begin{aligned}(1-r)\sum _{k=1}^{n}ar^{k-1}&=(1-r)\left(ar^{0}+ar^{1}+ar^{2}+ar^{3}+\cdots +ar^{n-1}\right)\\&=ar^{0}+ar^{1}+ar^{2}+ar^{3}+\cdots +ar^{n-1}-ar^{1}-ar^{2}-ar^{3}-\cdots -ar^{n-1}-ar^{n}\\&=a-ar^{n}\end{aligned}}}$$

поскольку все остальные условия отменяются. Если r ≠ 1, мы можем переставить приведенное выше, чтобы получить удобную формулу для геометрической прогрессии, которая вычисляет сумму n членов:

$${\displaystyle \sum _{k=1}^{n}ar^{k-1}={\frac {a(1-r^{n})}{1-r}}.}$$

Связанные формулы

Если бы начать суммирование не с k=1 или 0, а с другого значения, скажем , то ${\displaystyle m}$

$${\displaystyle {\begin{aligned}\sum _{k=m}^{n}ar^{k-1}&={\begin{cases}{\frac {a(r^{m-1}-r^{n})}{1-r}}&{\text{if }}r\neq 1\\a(n-m+1)&{\text{if }}r=1\end{cases}}\\\sum _{k=m}^{n}ar^{k}&={\begin{cases}a(n-m+1)&{\text{if }}r=1\\{\frac {a(r^{m}-r^{n+1})}{1-r}}&{\text{if }}r\neq 1\end{cases}}\end{aligned}}}$$

Дифференцирование этой формулы по позволяет прийти к формулам сумм вида ${\displaystyle r}$

$${\displaystyle G_{s}(n,r):=\sum _{k=0}^{n}k^{s}r^{k}.}$$

Например:

$${\displaystyle {\frac {d}{dr}}\sum _{k=0}^{n}r^{k}=\sum _{k=1}^{n}kr^{k-1}={\frac {1-r^{n+1}}{(1-r)^{2}}}-{\frac {(n+1)r^{n}}{1-r}}.}$$

Для геометрической прогрессии, содержащей только четные степени умножения на : ${\displaystyle r}$ ${\displaystyle 1-r^{2}}$

$${\displaystyle {\begin{aligned}(1-r^{2})\sum _{k=0}^{n}ar^{2k}&=a-ar^{2n+2}\\\sum _{k=0}^{n}ar^{2k}&={\frac {a(1-r^{2n+2})}{1-r^{2}}}\end{aligned}}}$$

Аналогично, возьмите обычное соотношение и используйте стандартную формулировку. ${\displaystyle r^{2}}$

Для ряда только с нечетными степенями , ${\displaystyle r}$

$${\displaystyle {\begin{aligned}(1-r^{2})\sum _{k=0}^{n}ar^{2k+1}&=ar-ar^{2n+3}\\\sum _{k=0}^{n}ar^{2k+1}&={\frac {ar(1-r^{2n+2})}{1-r^{2}}}&={\frac {a(r-r^{2n+3})}{1-r^{2}}}\end{aligned}}}$$

Точная формула обобщенной суммы при разложении числами Стирлинга второго рода как ^[6] ${\displaystyle G_{s}(n,r)}$ ${\displaystyle s\in \mathbb {N} }$

$${\displaystyle G_{s}(n,r)=\sum _{j=0}^{s}\left\lbrace {s \atop j}\right\rbrace x^{j}{\frac {d^{j}}{dx^{j}}}\left[{\frac {1-x^{n+1}}{1-x}}\right].}$$

Бесконечная серия

Бесконечная геометрическая серия — это бесконечная серия , последовательные члены которой имеют общее соотношение. Такой ряд сходится тогда и только тогда, когда абсолютное значение общего отношения меньше единицы (| r | < 1). Затем его значение можно вычислить по формуле конечной суммы

$${\displaystyle \sum _{k=0}^{\infty }ar^{k}=\lim _{n\to \infty }{\sum _{k=0}^{n}ar^{k}}=\lim _{n\to \infty }{\frac {a(1-r^{n+1})}{1-r}}={\frac {a}{1-r}}-\lim _{n\to \infty }{\frac {ar^{n+1}}{1-r}}}$$

Анимация, показывающая сходимость частичных сумм геометрической прогрессии (красная линия) к ее сумме (синяя линия) для . ${\displaystyle \sum \limits _{k=0}^{n}q^{k}}$ ${\displaystyle {1 \over 1-q}}$ ${\displaystyle |q|<1}$

Схема, показывающая геометрическую серию 1 + 1/2 + 1/4 + 1/8 + ⋯, сходящуюся к 2.

С:

$${\displaystyle r^{n+1}\to 0{\mbox{ as }}n\to \infty {\mbox{ when }}|r|<1.}$$

Затем:

$${\displaystyle \sum _{k=0}^{\infty }ar^{k}={\frac {a}{1-r}}-0={\frac {a}{1-r}}}$$

Для ряда, содержащего только четные степени , ${\displaystyle r}$

$${\displaystyle \sum _{k=0}^{\infty }ar^{2k}={\frac {a}{1-r^{2}}}}$$

$${\displaystyle \sum _{k=0}^{\infty }ar^{2k+1}={\frac {ar}{1-r^{2}}}}$$

В случаях, когда сумма не начинается с k = 0,

$${\displaystyle \sum _{k=m}^{\infty }ar^{k}={\frac {ar^{m}}{1-r}}}$$

рбанаховой алгебреrp -адических чисел,р_p

$${\displaystyle {\frac {d}{dr}}\sum _{k=0}^{\infty }r^{k}=\sum _{k=1}^{\infty }kr^{k-1}={\frac {1}{(1-r)^{2}}}}$$

Эта формула работает только для | р | <1 тоже. Отсюда следует, что при | р | < 1,

$${\displaystyle \sum _{k=0}^{\infty }kr^{k}={\frac {r}{\left(1-r\right)^{2}}}\,;\,\sum _{k=0}^{\infty }k^{2}r^{k}={\frac {r\left(1+r\right)}{\left(1-r\right)^{3}}}\,;\,\sum _{k=0}^{\infty }k^{3}r^{k}={\frac {r\left(1+4r+r^{2}\right)}{\left(1-r\right)^{4}}}}$$

Кроме того, бесконечный ряд 1/2 + 1/4 + 1/8 + 1/16 + ⋯ является элементарным примером ряда, который абсолютно сходится .

Это геометрическая прогрессия, первый член которой равен 1/2 и общее отношение которого равно 1/2, поэтому ее сумма равна

$${\displaystyle {\frac {1}{2}}+{\frac {1}{4}}+{\frac {1}{8}}+{\frac {1}{16}}+\cdots ={\frac {1/2}{1-(+1/2)}}=1.}$$

Обратный вышеприведенному ряду равен 1/2 - 1/4 + 1/8 - 1/16 + ⋯. Это простой пример знакопеременного ряда , который абсолютно сходится.

Это геометрическая прогрессия, первый член которой равен 1/2, а общее отношение равно -1/2, поэтому ее сумма равна

$${\displaystyle {\frac {1}{2}}-{\frac {1}{4}}+{\frac {1}{8}}-{\frac {1}{16}}+\cdots ={\frac {1/2}{1-(-1/2)}}={\frac {1}{3}}.}$$

Сложная серия

Формула суммирования геометрических рядов остается справедливой, даже если общее отношение является комплексным числом . В этом случае условием того, чтобы абсолютное значение r было меньше 1, становится то, чтобы модуль r был меньше 1. Можно вычислить суммы некоторых неочевидных геометрических рядов. Например, рассмотрим предложение

$${\displaystyle \sum _{k=0}^{\infty }{\frac {\sin(kx)}{r^{k}}}={\frac {r\sin(x)}{1+r^{2}-2r\cos(x)}}}$$

Доказательством этого является тот факт, что

$${\displaystyle \sin(kx)={\frac {e^{ikx}-e^{-ikx}}{2i}},}$$

формулы Эйлера

$${\displaystyle \sum _{k=0}^{\infty }{\frac {\sin(kx)}{r^{k}}}={\frac {1}{2i}}\left[\sum _{k=0}^{\infty }\left({\frac {e^{ix}}{r}}\right)^{k}-\sum _{k=0}^{\infty }\left({\frac {e^{-ix}}{r}}\right)^{k}\right].}$$

Это разность двух геометрических рядов, и поэтому доказательство завершается простым применением формулы бесконечной геометрической прогрессии.

История

Зенон Элейский (ок. 495 – ок. 430 до н. э.)

2500 лет назад у греческих математиков возникла проблема при переходе из одного места в другое: они думали ^[7] , что бесконечно длинный список чисел, больших нуля, в сумме дает бесконечность. Поэтому был парадокс, когда Зенон Элейский указывал, что для того, чтобы пройти из одного места в другое, нужно сначала пройти половину расстояния, затем нужно пройти половину оставшегося расстояния, а затем нужно пройти половину пути. оставшегося расстояния, и вы продолжаете сокращать оставшееся расстояние пополам бесконечное количество раз, потому что независимо от того, насколько мало оставшееся расстояние, вам все равно придется пройти первую его половину. Таким образом, Зенон Элейский превратил короткое расстояние в бесконечно длинный список пополам оставшихся расстояний, каждое из которых больше нуля. И в этом была проблема: как расстояние может быть коротким, если его измерить напрямую, и бесконечным, если суммировать его бесконечный список половинных остатков? Парадокс показал, что что-то не так с предположением, что бесконечно длинный список чисел больше нуля в сумме дает бесконечность.

Евклид Александрийский (ок. 300 г. до н. э.)

«Начала геометрии», книга IX, предложение 35. «Если существует какое-нибудь множество непрерывно пропорциональных чисел, равное первому, вычитается из второго и последнего, то как избыток второго над первым, так и избыток последним будет для всех, кто был до него».

Геометрическая интерпретация того же случая общего отношения r >1. (ВЕРХ) Представьте члены геометрической прогрессии как площади перекрывающихся подобных треугольников. (СРЕДНИЙ) От самого большого треугольника к самому маленькому удалите перекрывающуюся часть левой области (1/ r ) из неперекрывающейся части правой области (1-1/ r = ( r -1)/ r ) и масштабируйте эту неперекрывающуюся часть. перекрывающаяся трапеция на r /( r -1), поэтому ее площадь равна площади исходного перекрывающегося треугольника. (ВНИЗУ) Рассчитайте площадь совокупной трапеции как площадь большого треугольника минус площадь пустого маленького треугольника на левом кончике большого треугольника. Большой треугольник — это самый большой перекрывающийся треугольник, масштабированный r /( r -1). Пустой маленький треугольник начинался как a , но эта область была преобразована в неперекрывающуюся масштабированную трапецию, оставив пустую левую часть области (1/ r ). Однако этот пустой треугольник площадью a / r также должен быть масштабирован на r /( r -1), чтобы его наклон соответствовал наклону всех неперекрывающихся масштабированных трапеций. Следовательно, S _n = площадь большого треугольника - площадь пустого маленького треугольника = ar ⁿ⁺¹ /( r -1) - a /( r -1) = a ( r ⁿ⁺¹ -1)/( r -1) .

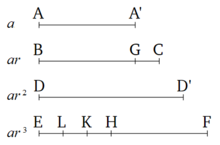
Элементы геометрии Евклида ^[8] Книга IX, предложение 35, доказательство (предложения в подписи к соседней диаграмме):

Пусть AA', BC, DD', EF — любое множество непрерывно пропорциональных чисел, начиная с наименьшего AA'. И пусть BG и FH, равные AA', вычтены из BC и EF. Я говорю, что GC относится к АА', а EH относится к АА', BC, DD'.

Ибо пусть FK будет равен BC, а FL — DD'. А поскольку FK равен BC, из которых FH равен BG, остаток HK, таким образом, равен остатку GC. И поскольку как EF относится к DD', так DD' относится к BC, а BC к AA' [Поп. 7.13], и DD' равен FL, BC - FK, а AA' - FH, таким образом, как EF соответствует FL, так и LF соответствует FK, а FK - FH. По разделению, как EL к LF, так и LK к FK, и KH к FH [Пол. 7.11, 7.13]. И таким образом, как одно из ведущих относится к одному из следующих, так и (сумма) всех ведущих к (сумме) всех следующих [Предл. 7.12]. Таким образом, как KH относится к FH, так и EL, LK, KH к LF, FK, HF. И КХ равен ЦГ, и ФХ - АА', и LF, FK, HF - ДД', ВС, АА'. Таким образом, как CG относится к AA', так и EH к DD', BC, AA'. Таким образом, как превышение второго по отношению к первому, так и превышение последнего по отношению ко всем предшествующим ему. То самое, что и требовалось показать.

Краткость предложений и доказательств Евклида могла быть необходимостью. В настоящее время «Элементы геометрии» — это более 500 страниц утверждений и доказательств. Изготовление копий этого популярного учебника было трудоемким, учитывая, что печатный станок был изобретен только в 1440 году. И популярность книги сохранялась долгое время: как сказано в цитированном предисловии к английскому переводу, « Элементы геометрии » «отличаются старейший в мире постоянно используемый учебник по математике». Так что быть очень кратким означало быть очень практичным. Доказательство предложения 35 в книге IX могло бы быть еще более компактным, если бы Евклид мог каким-то образом избежать явного приравнивания длин конкретных отрезков прямых из разных членов ряда. Например, современные обозначения геометрических рядов (т. е. a + ar + ar ² + ar ³ + ... + ar ⁿ ) не обозначают определенные части термов, которые равны друг другу.

Также в цитируемом предисловии редактор комментирует:

Большинство теорем, представленных в «Началах», не были открыты самим Евклидом, а были работой более ранних греческих математиков, таких как Пифагор (и его школа), Гиппократ Хиосский, Теэтет Афинский и Евдокс Книдский. Однако Евклиду обычно приписывают логическую организацию этих теорем, чтобы продемонстрировать (правда, не всегда со строгостью, требуемой современной математикой), что они обязательно следуют из пяти простых аксиом. Евклиду также приписывают разработку ряда особенно остроумных доказательств ранее открытых теорем (например, теоремы 48 в книге 1).

Чтобы помочь перевести предложение и доказательство в форму, использующую текущие обозначения, в диаграмму внесено несколько изменений. Во-первых, четыре длины горизонтальных линий, представляющие значения первых четырех членов геометрической прогрессии, теперь обозначены a, ar, ar ² , ar ³ на левом поле диаграммы. Во-вторых, новые метки A' и D' теперь находятся на первой и третьей строках, так что все имена сегментов линии диаграммы последовательно указывают начальную и конечную точки сегмента.

Вот пословное толкование предложения:

Аналогично, вот пословная интерпретация доказательства:

Архимед Сиракузский (ок. 287 – ок. 212 до н. э.)

Рассечение Архимедом параболического сегмента на бесконечное число треугольников

Архимед использовал сумму геометрической прогрессии для вычисления площади, ограниченной параболой и прямой линией. Его метод заключался в том, чтобы разрезать область на бесконечное количество треугольников.

Теорема Архимеда гласит, что общая площадь под параболой составляет 4/3 площади синего треугольника.

Архимед определил, что каждый зеленый треугольник имеет 1/8 площади синего треугольника, каждый желтый треугольник — 1/8 площади зеленого треугольника и так далее.

Если предположить, что площадь синего треугольника равна 1, общая площадь представляет собой бесконечную сумму:

${\displaystyle 1\,+\,2\left({\frac {1}{8}}\right)\,+\,4\left({\frac {1}{8}}\right)^{2}\,+\,8\left({\frac {1}{8}}\right)^{3}\,+\,\cdots .}$

Первое слагаемое представляет площадь синего треугольника, второе — площади двух зеленых треугольников, третье — площади четырех желтых треугольников и так далее. Упрощение дробей дает

${\displaystyle 1\,+\,{\frac {1}{4}}\,+\,{\frac {1}{16}}\,+\,{\frac {1}{64}}\,+\,\cdots .}$

Это геометрическая прогрессия с общим соотношением 1/4 и дробной частью, равной

${\displaystyle \sum _{n=0}^{\infty }4^{-n}=1+4^{-1}+4^{-2}+4^{-3}+\cdots ={4 \over 3}.}$

Сумма

${\displaystyle {\frac {1}{1-r}}\;=\;{\frac {1}{1-{\frac {1}{4}}}}\;=\;{\frac {4}{3}}.}$

В этом вычислении используется метод истощения , ранняя версия интегрирования . Используя математический анализ , ту же площадь можно найти с помощью определенного интеграла .

Николь Орем (ок. 1323–1382)

Двумерная диаграмма геометрических рядов, которую Николь Орем использовала, чтобы определить, что бесконечный ряд 1/2 + 2/4 + 3/8 + 4/16 + 5/32 + 6/64 + 7/128 + ... сходится к 2.

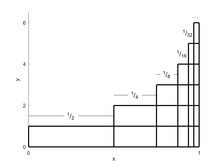
Среди своих идей о бесконечных рядах, в дополнение к элегантно простому доказательству расходимости гармонического ряда, Николь Орем ^[9] доказала, что ряд 1/2 + 2/4 + 3/8 + 4/16 + 5/32 + 6/64 + 7/128 + ... сходится к 2. Его диаграмма для его геометрического доказательства, аналогичная соседней диаграмме, показывает двумерную геометрическую серию. Первое измерение горизонтальное, в нижнем ряду показана геометрическая серия S = 1/2 + 1/4 + 1/8 + 1/16 + ... , которая представляет собой геометрическую серию с коэффициентом a = 1/2 и общим соотношение r = 1/2, которое сходится к S = a / (1- r ) = (1/2) / (1-1/2) = 1. Второе измерение вертикальное, где нижний ряд представляет собой новый коэффициент a _T равен S , и каждая последующая строка над ним масштабируется по тому же общему отношению r = 1/2, образуя еще одну геометрическую серию T = 1 + 1/2 + 1/4 + 1/8 + ..., которая является геометрическая прогрессия с коэффициентом a _T = S = 1 и общим отношением r = 1/2, сходящаяся к T = a _T / (1- r ) = S / (1- r ) = a / (1- r ) / (1 - г ) = (1/2)/(1-1/2)/(1-1/2) = 2.

Хотя идею Орема трудно визуализировать за пределами трех измерений, она распространяется на любое измерение d . Использование суммы размерности d -1 геометрической прогрессии в качестве коэффициента a в измерении d геометрической прогрессии приводит к тому, что d -мерная геометрическая серия сходится к S ^d / a = 1 / (1- r ) ^d в пределах диапазон | р |<1. Треугольник Паскаля и деление в столбики раскрывают коэффициенты этих многомерных геометрических рядов, где замкнутая форма действительна только в пределах диапазона | р |<1.

${\displaystyle {\begin{matrix}1\\1\quad 1\\1\quad 2\quad 1\\1\quad 3\quad 3\quad 1\\1\quad 4\quad 6\quad 4\quad 1\end{matrix}}}$

Кроме того, вместо использования деления в столбики также можно вычислить коэффициенты d -мерной геометрической прогрессии путем интегрирования коэффициентов размерности d -1. Это отображение от деления на 1- r в области суммы степенного ряда к интегрированию в области коэффициентов степенного ряда представляет собой дискретную форму отображения, выполняемого преобразованием Лапласа . Профессор Массачусетского технологического института Артур Мэттак показывает, как вывести преобразование Лапласа из степенного ряда в этом видеолекции, ^[10] где степенной ряд представляет собой отображение между дискретными коэффициентами и суммой, а преобразование Лапласа представляет собой отображение между непрерывными весами и интегралом.

Приложения

Экономика

В экономике геометрические ряды используются для представления текущей стоимости аннуитета (суммы денег, подлежащей выплате через равные промежутки времени) .

Например, предположим, что владельцу аннуитета будет выплачиваться 100 долларов один раз в год (в конце года) на постоянной основе . Получение 100 долларов через год стоит меньше, чем немедленные 100 долларов, потому что человек не может инвестировать деньги, пока не получит их. В частности, текущая стоимость 100 долларов США через год равна 100 долларов США / (1 +  ), где — годовая процентная ставка. ${\displaystyle I}$ ${\displaystyle I}$

Аналогичным образом, платеж в размере 100 долларов США через два года имеет текущую стоимость 100 долларов США / (1 +  ) ² (в квадрате, поскольку проценты за два года теряются из-за неполучения денег прямо сейчас). Следовательно, текущая стоимость постоянного получения 100 долларов в год равна ${\displaystyle I}$

${\displaystyle \sum _{n=1}^{\infty }{\frac {\$100}{(1+I)^{n}}},}$

что представляет собой бесконечный ряд:

${\displaystyle {\frac {\$100}{(1+I)}}\,+\,{\frac {\$100}{(1+I)^{2}}}\,+\,{\frac {\$100}{(1+I)^{3}}}\,+\,{\frac {\$100}{(1+I)^{4}}}\,+\,\cdots .}$

Это геометрическая прогрессия с общим соотношением 1/(1+  ). Сумма представляет собой первое слагаемое, разделенное на (один минус обыкновенное отношение): ${\displaystyle I}$

${\displaystyle {\frac {\$100/(1+I)}{1-1/(1+I)}}\;=\;{\frac {\$100}{I}}.}$

Например, если годовая процентная ставка составляет 10% (  = 0,10), то приведенная стоимость всего аннуитета составляет 100 долларов США / 0,10 = 1000 долларов США. ${\displaystyle I}$

Этот вид расчета используется для расчета годовой процентной ставки по кредиту (например, ипотечному кредиту ). Его также можно использовать для оценки текущей стоимости ожидаемых дивидендов по акциям или конечной стоимости финансового актива при условии стабильных темпов роста.

Фрактальная геометрия

Область внутри снежинки Коха можно описать как объединение бесконечного числа равносторонних треугольников (см. рисунок). Каждая сторона зеленого треугольника составляет ровно 1/3 размера стороны большого синего треугольника и, следовательно, имеет ровно 1/9 площади. Точно так же площадь каждого желтого треугольника составляет 1/9 площади зеленого треугольника и так далее. Если принять за единицу площади синий треугольник, то общая площадь снежинки составит

${\displaystyle 1\,+\,3\left({\frac {1}{9}}\right)\,+\,12\left({\frac {1}{9}}\right)^{2}\,+\,48\left({\frac {1}{9}}\right)^{3}\,+\,\cdots .}$

Первый член этого ряда представляет площадь синего треугольника, второй член — общую площадь трех зеленых треугольников, третий член — общую площадь двенадцати желтых треугольников и так далее. За исключением начальной 1, этот ряд является геометрическим с постоянным отношением r  = 4/9. Первый член геометрической прогрессии равен a  = 3(1/9) = 1/3, поэтому сумма равна

${\displaystyle 1\,+\,{\frac {a}{1-r}}\;=\;1\,+\,{\frac {\frac {1}{3}}{1-{\frac {4}{9}}}}\;=\;{\frac {8}{5}}.}$

Таким образом, снежинка Коха занимает 8/5 площади основания треугольника.

Интеграция

Производная от потому что, ^[11] позволяя ${\displaystyle f(x)=\arctan(u(x)){\text{ is }}f'(x)=u'(x)/(1+[u(x)]^{2})}$ ${\displaystyle y{\text{ and }}u{\text{ represent }}f(x){\text{ and }}u(x),}$

${\displaystyle {\begin{aligned}y&=\arctan(u)&&\quad {\text{ implies }}\\u&=\tan(y)&&\quad {\text{ in the range }}-\pi /2<y<\pi /2{\text{ and }}\\u'&=\sec ^{2}y\cdot y'&&\quad {\text{ by applying the quotient rule to }}\tan(y)=\sin(y)/\cos(y),\\y'&=u'/\sec ^{2}y&&\quad {\text{ by dividing both sides by }}\sec ^{2}y,\\&=u'/(1+\tan ^{2}y)&&\quad {\text{ by using the trigonometric identity derived by dividing }}\sin ^{2}y+\cos ^{2}y=1{\text{ by }}\cos ^{2}y,\\&=u'/(1+u^{2})&&\quad {\text{ by recalling }}u=\tan(y).\end{aligned}}}$

Следовательно, сдача в аренду является неотъемлемой частью ${\displaystyle u(x)=x,\arctan(x)}$

${\displaystyle {\begin{aligned}\arctan(x)&=\int {\frac {dx}{1+x^{2}}}\quad &&{\text{in the range }}-\pi /2<\arctan(x)<\pi /2,\\&=\int {\frac {dx}{1-(-x^{2})}}\quad &&{\text{by writing integrand as closed form of geometric series with }}r=-x^{2},\\&=\int \left(1+\left(-x^{2}\right)+\left(-x^{2}\right)^{2}+\left(-x^{2}\right)^{3}+\cdots \right)dx\quad &&{\text{by writing geometric series in expanded form}},\\&=\int \left(1-x^{2}+x^{4}-x^{6}+\cdots \right)dx\quad &&{\text{by calculating the sign and power of each term in integrand}},\\&=x-{\frac {x^{3}}{3}}+{\frac {x^{5}}{5}}-{\frac {x^{7}}{7}}+\cdots \quad &&{\text{by integrating each term}},\\&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{2n+1}}x^{2n+1}\quad &&{\text{by writing series in generator form}},\end{aligned}}}$

который называется серией Григория и обычно приписывается Мадхаве из Сангамаграмы (ок. 1340 – ок. 1425).

Экземпляры

• Ряд Гранди  – бесконечная сумма чередующихся членов 1 и -1: 1 – 1 + 1 – 1 + ⋯
• 1 + 2 + 4 + 8 + ⋯  – Бесконечная серия
• 1 − 2 + 4 − 8 + ⋯  – бесконечный рядPages displaying wikidata descriptions as a fallback
• 1/2 + 1/4 + 1/8 + 1/16 + ⋯  – Математический бесконечный ряд
• 1/2 − 1/4 + 1/8 − 1/16 + ⋯  – математический бесконечный рядPages displaying wikidata descriptions as a fallback
• 1/4 + 1/16 + 1/64 + 1/256 + ⋯  – Бесконечная сумма, равная 1/3 на своем пределе.
• Геометрическая серия является единичной (сумма ряда сходится к единице) тогда и только тогда, когда | р | < 1 и a + r = 1 (эквивалент более знакомой форме S = a / (1 - r ) = 1, когда | r | < 1). Следовательно, знакопеременный ряд также является единичным рядом, когда -1 < r < 0 и a + r = 1 (например, коэффициент a = 1,7 и общий коэффициент r = -0,7).
• Члены геометрического ряда также являются членами обобщенной последовательности Фибоначчи (F _n = F _n-1 + F _n-2 , но без требования F ₀ = 0 и F _{1 = 1), когда общее отношение} r геометрического ряда удовлетворяет условию ограничение 1 + r = r ² , которое согласно квадратичной формуле возникает, когда общее отношение r равно золотому сечению (т. е. общее отношение r = (1 ± √5)/2).
• Единственная геометрическая серия, которая является единичным рядом и также имеет члены обобщенной последовательности Фибоначчи , имеет золотое сечение в качестве коэффициента a и сопряженное золотое сечение в качестве общего отношения r (т. е. a = (1 + √5)/2 и г = (1 - √5)/2). Это единичная серия, поскольку a + r = 1 и | р | < 1, это обобщенная последовательность Фибоначчи , поскольку 1 + r = r ² , и знакопеременная серия, поскольку r < 0.

Геометрическая серия

Компактная иллюстрация различных точек зрения на геометрический ряд, упрощающая переключение перспектив. Квадрант A1 содержит точку зрения «почему» , кратко описывающую, почему геометрические ряды имеют значение. Квадрант A2 содержит перспективный список фрагмента кода Джулии, вычисляющего геометрическую прогрессию. Квадрант A3 содержит перспективу « что» (алгебра) с алгебраическим доказательством формулы замкнутой формы геометрического ряда. Квадрант A4 содержит перспективу « что» (геометрия), показывающую три этапа геометрического доказательства формулы замкнутой формы геометрического ряда. А на правом поле показана временная шкала некоторых исторических представлений о геометрических рядах.

Геометрическая прогрессия имеет две степени свободы: одну для коэффициента а и другую для общего отношения r . На карте полиномов большой красный круг представляет собой набор всех геометрических рядов.

Сходящиеся геометрические ряды

Лишь часть всех геометрических рядов сходится. В частности, геометрическая прогрессия сходится тогда и только тогда, когда ее общее отношение | р | < 1. На карте полиномов красный треугольник представляет набор сходящихся геометрических рядов, а то, что он нарисован внутри большого красного круга, представляющего набор всех геометрических рядов, указывает на то, что сходящийся геометрический ряд является подмножеством геометрического ряда.

Повторяющиеся десятичные дроби

Только подмножество всех сходящихся геометрических рядов сходится к десятичным дробям, которые имеют повторяющиеся закономерности, продолжающиеся вечно (например, 0,7777... или 0,9999... или 0,123412341234...). На карте полиномов маленький желтый треугольник представляет собой набор геометрических рядов, которые сходятся к бесконечно повторяющимся десятичным закономерностям. Он нарисован внутри красного треугольника, чтобы указать, что он является подмножеством сходящейся геометрической серии, которая, в свою очередь, нарисована внутри большого красного круга, указывая, что как сходящиеся геометрические ряды, так и геометрические ряды, которые сходятся к бесконечно повторяющимся закономерностям, являются подмножествами геометрических рядов. ряд.

Хотя дроби с бесконечно повторяющимися десятичными шаблонами можно аппроксимировать только в том случае, если они закодированы как числа с плавающей запятой, их всегда можно определить точно как отношение двух целых чисел, и эти два целых числа можно вычислить с помощью геометрической прогрессии. Например, повторяющуюся десятичную дробь 0,7777... можно записать в виде геометрической прогрессии.

${\displaystyle 0.7777\ldots \;=\;{\frac {7}{10}}\,+\,{\frac {7}{10}}{\frac {1}{10}}\,+\,{\frac {7}{10}}{\frac {1}{10^{2}}}\,+\,{\frac {7}{10}}{\frac {1}{10^{3}}}\,+\,\cdots }$

где коэффициент a = 7/10 и общий коэффициент r = 1/10. Замкнутая форма геометрической серии показывает два целых числа, которые определяют повторяющийся шаблон:

${\displaystyle 0.7777\ldots \;=\;{\frac {a}{1-r}}\;=\;{\frac {7/10}{1-1/10}}\;=\;{\frac {7/10}{9/10}}\;=\;{\frac {7}{9}}.}$

Этот подход выходит за рамки десятичных чисел. Фактически, любая дробь, имеющая бесконечно повторяющийся образец в числах с основанием десять, также имеет бесконечно повторяющийся образец в числах, записанных в любой другой системе счисления. Например, глядя на кодировку с плавающей запятой для числа 0,7777...

julia> bitstring(Float32(0.77777777777777777777))
"00111111010001110001110001110010"

показывает двоичную дробь 0,110001110001110001... где двоичный шаблон 0b110001 повторяется бесконечно и может быть записан в основном (за исключением степеней) двоичными числами как

${\displaystyle 0.110001110001110001\ldots \;=\;{\frac {110001}{1000000}}\,+\,{\frac {110001}{1000000}}{\frac {1}{1000000}}\,+\,{\frac {110001}{1000000}}{\frac {1}{1000000^{2}}}\,+\,{\frac {110001}{1000000}}{\frac {1}{1000000^{3}}}\,+\,\cdots }$

где коэффициент a = 0b110001/0b1000000 = 49/64 и общее отношение r = 1/0b1000000 = 1/64. Используя замкнутую форму геометрического ряда, как и раньше

${\displaystyle 0.7777\ldots \;=\;0b0.110001110001110001\ldots \;=\;{\frac {a}{1-r}}\;=\;{\frac {49/64}{1-1/64}}\;=\;{\frac {49/64}{63/64}}\;=\;{\frac {49}{63}}\;=\;{\frac {7}{9}}.}$

Возможно, вы заметили, что кодирование с плавающей запятой не фиксирует шаблон повторения 0b110001 в последних паре (наименее значимых) битов. Это связано с тем, что кодирование с плавающей запятой округляет остаток, а не усекает его. Следовательно, если наиболее значимый бит остатка равен 1, младший бит закодированной дроби увеличивается, и это вызовет перенос, если младший бит остатка уже равен 1, что может вызвать еще один перенос, если этот бит дробь уже равна 1, что может вызвать еще один перенос и т. д. Это округление с плавающей запятой и последующее распространение переноса объясняют, почему кодировка с плавающей запятой для 0,99999... точно такая же, как кодировка с плавающей запятой для 1.

julia> bitstring(Float32(0.99999999999999999999))
"00111111100000000000000000000000"

julia> bitstring(Float32(1.0))
"00111111100000000000000000000000"

Например, в повторяющемся шаблоне четыре цифры: 0,123412341234... можно записать в виде геометрической прогрессии.

${\displaystyle 0.123412341234\ldots \;=\;{\frac {1234}{10000}}\,+\,{\frac {1234}{10000}}{\frac {1}{10000}}\,+\,{\frac {1234}{10000}}{\frac {1}{10000^{2}}}\,+\,{\frac {1234}{10000}}{\frac {1}{10000^{3}}}\,+\,\cdots }$

где коэффициент a = 1234/10000 и общий коэффициент r = 1/10000. Замкнутая форма геометрической серии показывает два целых числа, которые определяют повторяющийся шаблон:

${\displaystyle 0.123412341234\ldots \;=\;{\frac {a}{1-r}}\;=\;{\frac {1234/10000}{1-1/10000}}\;=\;{\frac {1234/10000}{9999/10000}}\;=\;{\frac {1234}{9999}}.}$

Силовая серия

Как и геометрический ряд, степенной ряд имеет одну степень свободы для своего общего отношения r (вдоль оси x), но имеет n +1 степень свободы для своих коэффициентов (вдоль оси y), где n представляет собой степень последний член частичного ряда. На карте полиномов большой синий круг представляет собой набор всех степенных рядов.

Серия Тейлора

По мере повышения степени полинома Тейлора он приближается к правильной функции. На этом изображении показаны sin x и его аппроксимации Тейлора полиномами степени 1 , 3 , 5 , 7 , 9 , 11 и 13 при x = 0 .

В математике ряд Тейлора или разложение Тейлора функции представляет собой бесконечную сумму членов, которые выражаются через производные функции в одной точке. Для большинства распространенных функций функция и сумма ее ряда Тейлора равны вблизи этой точки. Ряды Тейлора названы в честь Брука Тейлора , который представил их в 1715 году. Ряд Тейлора также называется рядом Маклорена, когда 0 — это точка, в которой рассматриваются производные, в честь Колина Маклорена , который широко использовал этот особый случай ряда Тейлора в 18 век.

Частичная сумма , образованная первыми n + 1 членами ряда Тейлора, представляет собой многочлен степени n , который называется n -м полиномом Тейлора функции. Полиномы Тейлора — это аппроксимации функции, которые обычно становятся более точными по мере увеличения n . Теорема Тейлора дает количественные оценки ошибки, вносимой использованием таких приближений. Если ряд Тейлора функции сходится , его сумма является пределом бесконечной последовательности полиномов Тейлора. Функция может отличаться от суммы своего ряда Тейлора, даже если ее ряд Тейлора сходится. Функция является аналитической в ​​точке x , если она равна сумме своего ряда Тейлора на некотором открытом интервале (или открытом круге в комплексной плоскости ), содержащем x . Это означает, что функция аналитична в каждой точке интервала (или круга).

Двоичные кодированные числа

Геометрическая серия Зенона Элеа с коэффициентом a = 1/2 и общим отношением r = 1/2 является основой двоично-кодированных аппроксимаций дробей в цифровых компьютерах. Конкретно, геометрическая прогрессия, записанная в нормализованной векторной форме, равна s / a = [1 1 1 1 1 …][1 r r ² r ³ r ⁴  …] ^T . Сохранение вектора-столбца базисных функций [1 r r ² r ³ r ⁴ …] ^T таким же, но обобщение вектора-строки [1 1 1 1 1 …] так, чтобы каждая запись могла быть либо 0, либо 1, позволяет получить приблизительное значение. кодирование любой дроби. Например, значение v = 0,34375 кодируется как  v / a = [0 1 0 1 1 0 …][1 r r ² r ³ r ⁴ …] ^T , где коэффициент a = 1/2 и общий коэффициент r = 1/ 2. Обычно вектор-строка записывается в более компактной двоичной форме v = 0,010110, что составляет 0,34375 в десятичном виде.

Точно так же геометрическая прогрессия с коэффициентом a =1 и общим отношением r =2 является основой для целых чисел в двоичном кодировании в цифровых компьютерах. Опять же, геометрическая прогрессия, записанная в нормализованной векторной форме, равна s / a = [1 1 1 1 1 …][1 r r ² r ³ r ⁴ …] ^T . Сохранение вектора-столбца базисных функций [1 r r ² r ³ r ⁴ …] ^T таким же, но обобщение вектора-строки [1 1 1 1 1 …] так, чтобы каждая запись могла быть либо 0, либо 1, позволяет кодировать любого целого числа. Например, значение v = 151 кодируется как  v / a = [1 1 1 0 1 0 0 1 0 …][1 r r ² r ³ r ⁴ r ⁵ r ⁶ r ⁷ r ⁸ …] ^T , где коэффициент a = 1 и общее отношение r = 2. Обычно вектор-строка записывается в обратном порядке (так, чтобы самый старший бит был первым) в более компактной двоичной форме v = …010010111 = 10010111, что равно 151 в десятичном виде.

Битовые поля для кодирования 32-битного числа с плавающей запятой в соответствии со стандартом IEEE 754.

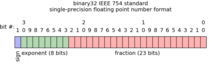
Как показано на соседнем рисунке, стандартное двоичное кодирование 32-битного числа с плавающей запятой представляет собой комбинацию двоичного целого числа и двоичной дроби, начиная со старшего бита с

• знаковый бит, за которым следует
• 8-битное целочисленное поле показателя степени с предполагаемым смещением 127 (поэтому значение 127 представляет значение показателя степени 0) и с основанием 2, что означает, что значение показателя степени определяет битовый сдвиг поля дроби, за которым следует
• 23-битное поле дроби с предполагаемой, но не закодированной единицей, служащее старшим ненулевым битом дроби, который находился бы в битовой позиции 23, если бы он был закодирован.

Основываясь на предыдущем примере 0,34375 с двоичной кодировкой 0,010110, кодировка с плавающей запятой (согласно стандарту IEEE 754) 0,34375 равна

• знаковый бит, который равен 0, поскольку число не является отрицательным,
• 8-битное целочисленное поле экспоненты, которое должно указывать сдвиг, который противодействует 2-битному сдвигу влево, чтобы получить исходную двоичную кодировку от 0,010110 до 1,0110, и этот сдвиг счетчика для восстановления исходной двоичной кодировки представляет собой сдвиг вправо на 2 бита, который указан на значение показателя степени 125 (поскольку 125 - 127 = -2, что представляет собой сдвиг вправо на 2 бита), что в двоичном формате равно 0111 1101,
• 23-битное поле дроби: 0,0110 0000 0000 0000 0000 000.

Хотя кодирование чисел с плавающей запятой вручную возможно, позволить компьютеру сделать это проще и менее подвержено ошибкам. Следующий код Julia подтверждает вычисленное вручную кодирование числа 0,34375 с плавающей запятой:

julia> bitstring(Float32(0.34375))
"00111110101100000000000000000000"

Лоран серии

Ряд Лорана определяется относительно конкретной точки и пути интегрирования γ. Путь интегрирования должен лежать в кольце, обозначенном здесь красным цветом, внутри которого голоморфно ( аналитически ) . ${\displaystyle c}$ ${\displaystyle f(z)}$

В математике ряд Лорана сложной функции представляет собой представление этой функции в виде степенного ряда , включающего члены отрицательной степени. Его можно использовать для выражения сложных функций в тех случаях, когда невозможно применить разложение в ряд Тейлора . Серия Лорана была названа в честь Пьера Альфонса Лорана и впервые опубликована в 1843 году. Карл Вейерштрасс, возможно, впервые обнаружил ее в статье, написанной в 1841 году, но она была опубликована только после его смерти. ^[12] ${\displaystyle f(z)}$

Комплексный ряд Фурье

Передняя и задняя плоскости показывают сумму первых +/-n членов комплексного ряда Фурье, коэффициенты которого установлены так, чтобы сходиться к следу буквы «е» для экспоненты. (Исходный код Julia, который генерирует кадры и звук этой анимации, находится здесь ^[13] в Приложении B.)

В качестве примера способности сложного ряда Фурье отслеживать любую двумерную замкнутую фигуру можно привести в соседней анимации сложный ряд Фурье, отслеживающий букву «е» (для экспоненты). Учитывая сложную координацию движений, показанную в анимации, определение сложного ряда Фурье может быть на удивление компактным, состоящим всего из двух уравнений:

${\displaystyle {\begin{aligned}s(t)&=\sum _{n=-\infty }^{\infty }c_{n}e^{2\pi int}\\c_{n}&=\int _{0}^{1}s(t)e^{-2\pi int}dt\\\end{aligned}}}$

где параметризованная функция s ( t ) отслеживает некоторую двумерную замкнутую фигуру в комплексной плоскости по мере того, как параметр t проходит через период от 0 до 1.

Чтобы помочь понять смысл этих компактных уравнений, определяющих комплексный ряд Фурье, обратите внимание, что суммирование комплексного ряда Фурье похоже на комплексный геометрический ряд, за исключением того, что комплексный ряд Фурье по сути представляет собой два комплексных геометрических ряда (один набор членов, вращающихся в положительном направлении). и еще один набор членов, вращающихся в отрицательном направлении), а коэффициенты комплексного ряда Фурье представляют собой комплексные константы, которые могут меняться от члена к члену. Позволяя членам вращаться в любом направлении, серия становится способной отслеживать любую замкнутую двумерную фигуру. Напротив, в сложной геометрической прогрессии все члены вращаются в одном направлении, и она может чертить только круги. Разрешение коэффициентам сложного геометрического ряда изменяться от члена к члену приведет к расширению форм, которые он может отслеживать, но все возможные формы по-прежнему будут ограничены раздутыми и похожими на облака, неспособными проследить форму простого отрезка линии. , например, переходя туда и обратно между 1 + i0 и -1 + i0. Однако формула Эйлера показывает, что добавление всего двух членов, вращающихся в противоположных направлениях, может проследить этот отрезок между 1 + i0 и -1 + i0:

${\displaystyle {\begin{aligned}e^{i\theta }&=\cos \theta +i\sin \theta \\e^{-i\theta }&=\cos \theta -i\sin \theta \\\cos \theta &={\frac {e^{i\theta }+e^{-i\theta }}{2}}.\\\end{aligned}}}$

Что касается второго уравнения комплексного ряда Фурье, определяющего способ расчета коэффициентов, то коэффициент невращающегося члена c ₀ можно рассчитать путем интегрирования первого уравнения комплексного ряда Фурье в диапазоне одного периода от 0 до 1. В этом диапазоне все вращающиеся члены интегрируются до нуля, остается только c ₀ . Аналогично, любой из членов первого уравнения комплексного ряда Фурье можно сделать невращающимся членом, умножив обе части уравнения на перед интегрированием для вычисления c _n , и это будет второе уравнение комплексного ряда Фурье. ${\displaystyle e^{-2\pi int}}$

Матричный полином

В математике матричный полином — это многочлен с квадратными матрицами в качестве переменных. Учитывая обычный скалярный полином

${\displaystyle P(x)=\sum _{i=0}^{n}{a_{i}x^{i}}=a_{0}+a_{1}x+a_{2}x^{2}+\cdots +a_{n}x^{n},}$

этот многочлен, оцененный в матрице, равен ${\displaystyle A}$

${\displaystyle P(A)=\sum _{i=0}^{n}{a_{i}A^{i}}=a_{0}I+a_{1}A+a_{2}A^{2}+\cdots +a_{n}A^{n},}$

где единичная матрица . ^[14] ${\displaystyle I}$

Обратите внимание, что он имеет тот же размер, что и . ${\displaystyle P(A)}$ ${\displaystyle A}$

Матричное полиномиальное уравнение — это равенство между двумя матричными полиномами, которое справедливо для конкретных рассматриваемых матриц. Матричное полиномиальное тождество — это матричное полиномиальное уравнение, которое справедливо для всех матриц A в заданном кольце матриц M _n ( R ).

Матричные полиномы часто демонстрируются на курсах линейной алгебры студентов бакалавриата из-за их актуальности для демонстрации свойств линейных преобразований, представленных в виде матриц, в первую очередь теоремы Кэли-Гамильтона .

Матричная экспонента

В математике матричная экспонента — это матричная функция на квадратных матрицах , аналогичная обычной экспоненциальной функции . Он используется для решения систем линейных дифференциальных уравнений. В теории групп Ли матричная экспонента дает экспоненциальное отображение между матричной алгеброй Ли и соответствующей группой Ли .

Пусть X — действительная или комплексная матрица размера n × n . Экспонента X , обозначаемая e ^X или exp( X ) , представляет собой матрицу размера n × n , заданную степенным рядом

$${\displaystyle e^{X}=\sum _{k=0}^{\infty }{\frac {1}{k!}}X^{k}}$$

где определяется как единичная матрица тех же размеров, что и . ^[15] Ряд всегда сходится, поэтому экспонента X четко определена. ${\displaystyle X^{0}}$ ${\displaystyle I}$ ${\displaystyle X}$

Эквивалентно,

$${\displaystyle e^{X}=\lim _{k\rightarrow \infty }\left(I+{\frac {X}{k}}\right)^{k}}$$

где I — единичная матрица размера n × n . Когда X является диагональной матрицей размера n × n, тогда exp( X ) будет диагональной матрицей размера n × n , где каждый диагональный элемент равен обычной экспоненте , примененной к соответствующему диагональному элементу X .

Аналогичный случай для квадрата индекса в экспоненте

Определения тэта-функций

В геометрическом ряду слагаемые имеют экспоненциальный ход по отношению к индексу суммы. Показатель степени в слагаемых, зависящий от индекса суммы, имеет линейный ход относительно индекса. Однако, если вместо этого показатель степени в элементах последовательности принимает квадратичный ход по отношению к индексу суммы, то сами члены последовательности следуют по гауссовой колоколообразной кривой , и тогда значения затронутой бесконечной серии не могут быть отображены. элементарным образом. Суммы с квадратичным ходом показателя степени в членах последовательности относительно индекса суммы принимают значения эллиптической тета-функции для представления. И эти значения могут быть представлены как с помощью тета-функций Якобиана , так и с помощью тета-функций Невилла .

Упомянутые тета-функции соответствуют Эдмунду Тейлору Уиттакеру и Джорджу Невиллу Уотсону. Тета-функции ^{[16] [17] [18]} определяются следующим образом:

${\displaystyle \vartheta _{00}(v;w)=\prod _{n=1}^{\infty }(1-w^{2n})[1+2\cos(2v)w^{2n-1}+w^{4n-2}]}$

${\displaystyle \theta _{d}(y;k)=\prod _{n=1}^{\infty }{\bigl [}1+q(k)^{2n-1}{\bigr ]}^{-2}{\bigl \{}1+2q(k)^{2n-1}\cos {\bigl [}\pi \,y\div K(k){\bigr ]}+q(k)^{4n-2}{\bigr \}}}$

Функция называется эллиптическим номом и обозначает полный эллиптический интеграл первого рода: ${\displaystyle q(k)}$ ${\displaystyle K(k)}$

${\displaystyle q(k)=\exp {\bigl [}-\pi \,K({\sqrt {1-k^{2}}}\,)\div K(k){\bigr ]}=\exp {\bigl [}-\pi \,K'(k)\div K(k){\bigr ]}}$

${\displaystyle K(\varepsilon )=\int _{0}^{1}{\bigl [}(1-z^{2})(1-\varepsilon ^{2}z^{2}){\bigr ]}^{-1/2}\,\mathrm {d} z}$

${\displaystyle K'(\varepsilon )=K({\sqrt {1-\varepsilon ^{2}}}\,)}$

Обозначение греческой буквы представляет собой так называемую Тета-функцию Нульверта , тогда как это обозначение обозначает эллиптическую пси-функцию Эрмита: ${\displaystyle \vartheta _{00}}$ ${\displaystyle \psi _{H}}$

${\displaystyle \vartheta _{00}(w)=\prod _{n=1}^{\infty }(1-w^{2n})(1+w^{2n-1})^{2}}$

${\displaystyle \psi _{H}(w)=\prod _{n=1}^{\infty }{\frac {1-w^{2n-1}}{1+w^{2n-1}}}}$

Тождества для суммарного ряда

Эта взаимосвязь дана:

Сами тета-функции Невилла исследовал математик Эрик Гарольд Невилл из Англии. В общем, при прохождении целочисленных шагов результат всегда должен быть одним и тем же значением снова и снова. Само это явление называется периодичностью функций. И этому критерию отвечают упомянутые выше тэта-формулы. Если R установлен в ноль, то результатом должно быть первичное стандартизованное значение тета-функции, базовое значение должно использоваться в качестве записи Nome функции Theta Nullwert. И если значение приводит не к целому числу, а к дробному числу, то результирующее значение ряда суммы должно быть связано со значением ряда суммы с равным нулю коэффициентом, который задается соответствующей неполной тэтой. функцией дополнительного имени , т.е. точно по значению . Формула в нижней строке показанной таблицы формул следует непосредственно из законов, описанных в двух последних упомянутых предложениях. И формула с тэта-функцией Невилла вытекает непосредственно из этого. В качестве модуля необходимо ввести дополнительный модуль Пифагора. И это точно создается четвертой степенью эллиптической пси-функции Эрмита . Используя эмпирическую формулу Пуассона , можно упростить формулу в нижней строке таблицы. ${\displaystyle R}$ ${\displaystyle \vartheta _{00}(Q)}$ ${\displaystyle Q}$ ${\displaystyle R}$ ${\displaystyle R}$ ${\displaystyle \vartheta _{00}(\pi \,R;Q')\div \vartheta _{00}(Q')}$ ${\displaystyle \psi _{H}(Q)^{4}}$

Примеры расчета с тетой Якоби

Эта формула о тэта-функции Якоби действительна:

${\displaystyle \sum _{n=-\infty }^{\infty }x^{an^{2}+bn+c}=\exp {\biggl [}{\frac {1}{4a}}(4ac-b^{2})\ln(x){\biggr ]}{\biggl [}{\frac {\pi }{a\ln(1\div x)}}{\biggr ]}^{1/2}\vartheta _{00}{\biggl \{}{\frac {\pi b}{2a}};\exp {\biggl [}{\frac {-\pi ^{2}}{a\ln(1\div x)}}{\biggr ]}{\biggr \}}}$

Hierfür sollgelten: ${\displaystyle (0<x<1)\,\,\cap \,\,(a\in \mathbb {R} ^{+})}$

Для упомянутого выше ряда сумм необходимо подробно выполнить следующие два примера расчета:

${\displaystyle \sum _{n=-\infty }^{\infty }{\bigl (}{\frac {7}{11}}{\bigr )}^{5n^{2}+3n+2}={\bigl (}{\frac {7}{11}}{\bigr )}^{31/20}{\bigl (}{\frac {\pi }{5}}{\bigr )}^{1/2}\ln {\bigl (}{\frac {11}{7}}{\bigr )}^{-1/2}\vartheta _{00}{\biggl \{}{\frac {3\pi }{10}};\exp {\biggl [}-{\frac {\pi ^{2}}{5}}\ln {\bigl (}{\frac {11}{7}}{\bigr )}^{-1}{\biggr ]}{\biggr \}}}$

${\displaystyle \sum _{n=-\infty }^{\infty }{\bigl (}{\frac {23}{29}}{\bigr )}^{19n^{2}+17n+13}={\bigl (}{\frac {23}{29}}{\bigr )}^{699/76}{\bigl (}{\frac {\pi }{19}}{\bigr )}^{1/2}\ln {\bigl (}{\frac {29}{23}}{\bigr )}^{-1/2}\vartheta _{00}{\biggl \{}{\frac {17\pi }{38}};\exp {\biggl [}-{\frac {\pi ^{2}}{19}}\ln {\bigl (}{\frac {29}{23}}{\bigr )}^{-1}{\biggr ]}{\biggr \}}}$

Смотрите также

• 0,999...  – Альтернативное десятичное расширение 1
• Асимптота  - предел касательной в точке, стремящейся к бесконечности.
• Расходящиеся геометрические ряды
• Обобщенная гипергеометрическая функция  - Семейство степенных рядов в математике
• Геометрическая прогрессия  – Математическая последовательность чисел.
• Ряд Неймана  – Математический ряд
• Тест на соотношение  - критерий сходимости ряда.
• Корневой тест  - Критерий сходимости бесконечного ряда.
• Ряд (математика)  – Бесконечная сумма
• Арифметический ряд  – Последовательность чиселPages displaying short descriptions of redirect targets

Примечания

1. Riddle, Дуглас Ф. Исчисление и аналитическая геометрия, второе издание Бельмонт, Калифорния, Wadsworth Publishing, стр. 566, 1970.
2. Хайрер Э.; Ваннер Г. (1996). Анализ по истории . Спрингер. п. 188.Раздел III.2, рисунок 2.1
3. Абрамовиц и Стегун (1972, стр. 10)
4. Мойзе (1967, стр. 48)
5. Проттер и Морри (1970, стр. 639–640)
6. «Установить разделы: числа Стирлинга» . Электронная библиотека математических функций . Проверено 24 мая 2018 г.
7. Риддл, Дуглас Э. (1974). Исчисление и аналитическая геометрия (2-е изд.). Издательство Уодсворт. п. 556. ИСБН 053400301-Х.
8. Евклид; Дж. Л. Хейберг (2007). Элементы геометрии Евклида (PDF) . Перевод Ричарда Фицпатрика. Ричард Фицпатрик. ISBN 978-0615179841. Архивировано (PDF) из оригинала 11 августа 2013 г.
9. Бэбб, Дж (2003). «Математические концепции и доказательства Николь Орем: использование истории исчисления для преподавания математики» (PDF) . Виннипег: Седьмая Международная конференция по истории, философии и естествознанию. стр. 11–12, 21. Архивировано (PDF) из оригинала 27 мая 2021 г.
10. Мэттук, Артур. «Лекция 19, Массачусетский технологический институт 18.03 Дифференциальные уравнения, весна 2006 г.». MIT OpenCourseWare. Архивировано из оригинала 11 ноября 2021 г.
11. Риддл, Дуглас (1974). Исчисление и аналитическая геометрия (второе изд.). Калифорния: Издательство Wadsworth. п. 310. ИСБН 0-534--00301-X.
12. Родригес, Руби; Кра, Ирвин; Гилман, Джейн П. (2012), Комплексный анализ: в духе Липмана Берса, Тексты для выпускников по математике, том. 245, Спрингер, с. 12, ISBN 9781441973238.
13. Сепеси, Г. (13 февраля 2022 г.). «Непреходящий пример Зенона». На пути к науке о данных. стр. Приложение Б.
14. Хорн и Джонсон 1990, с. 36.
15. Холл, 2015 г., уравнение 2.1.
16. Вайсштейн, Эрик В. «Тэта-функции Якоби». Математический мир .
17. http://wayback .cecm.sfu.ca/~pborwein/TEMP_PROTECTED/pi-agm.pdf
18. «DLMF: 20.5 бесконечных продуктов и связанные результаты» . Проверено 13 августа 2022 г.

Рекомендации

• Абрамовиц, М.; Стегун, Айова, ред. (1972). Справочник по математическим функциям с формулами, графиками и математическими таблицами (9-е печатное изд.). Нью-Йорк: Дувр. п. 10.
• Эндрюс, Джордж Э. (1998). «Геометрическая прогрессия в исчислении». Американский математический ежемесячник . Математическая ассоциация Америки. 105 (1): 36–40. дои : 10.2307/2589524. JSTOR  2589524.
• Арфкен, Г. Математические методы для физиков, 3-е изд. Орландо, Флорида: Academic Press, стр. 278–279, 1985.
• Бейер, Стандартные математические таблицы WH CRC, 28-е изд. Бока-Ратон, Флорида: CRC Press, с. 8, 1987.
• Курант Р. и Роббинс Х. «Геометрическая прогрессия». §1.2.3 в книге «Что такое математика?: Элементарный подход к идеям и методам», 2-е изд. Оксфорд, Англия: Издательство Оксфордского университета, стр. 13–14, 1996.
• Холл, Брайан К. (2015), Группы Ли, алгебры Ли и представления: элементарное введение , Тексты для выпускников по математике, том. 222 (2-е изд.), Спрингер, ISBN 978-3-319-13466-6
• Хорн, Роджер А.; Джонсон, Чарльз Р. (1990). Матричный анализ . Издательство Кембриджского университета. ISBN 978-0-521-38632-6..
• Джеймс Стюарт (2002). Исчисление , 5-е изд., Брукс Коул. ISBN 978-0-534-39339-7 
• Ларсон, Хостетлер и Эдвардс (2005). Исчисление с аналитической геометрией , 8-е изд., Houghton Mifflin Company. ISBN 978-0-618-50298-1 
• Мойс, Эдвин Э. (1967), Исчисление: полное , Чтение: Аддисон-Уэсли
• Паппас Т. «Периметр, площадь и бесконечная серия». Радость математики. Сан-Карлос, Калифорния: Wide World Publ./Tetra, стр. 134–135, 1989.
• Проттер, Мюррей Х.; Морри, Чарльз Б. младший (1970), Колледжское исчисление с аналитической геометрией (2-е изд.), Чтение: Аддисон-Уэсли , LCCN  76087042
• Роджер Б. Нельсен (1997). Доказательства без слов: упражнения на визуальное мышление , Математическая ассоциация Америки. ISBN 978-0-88385-700-7 

История и философия

• CH Эдвардс младший (1994). Историческое развитие исчисления , 3-е изд., Springer. ISBN 978-0-387-94313-8 . 
• Суэйн, Гордон и Томас Денс (апрель 1998 г.). «Возвращение к квадратуре параболы Архимеда». Журнал «Математика» . 71 (2): 123–30. дои : 10.2307/2691014. JSTOR  2691014.
• Эли Маор (1991). К бесконечности и за ее пределами: культурная история бесконечности , Princeton University Press. ISBN 978-0-691-02511-7 
• Морр Лазеровиц (2000). Структура метафизики (Международная философская библиотека) , Рутледж. ISBN 978-0-415-22526-7 

Экономика

• Карл П. Саймон и Лоуренс Блюм (1994). Математика для экономистов , WW Norton & Company. ISBN 978-0-393-95733-4 
• Майк Россер (2003). Основная математика для экономистов , 2-е изд., Routledge. ISBN 978-0-415-26784-7 

Биология

• Эдвард Батчелет (1992). Введение в математику для ученых-биологов , 3-е изд., Springer. ISBN 978-0-387-09648-3 
• Ричард Ф. Бертон (1998). Биология в числах: поощрение количественного мышления , Издательство Кембриджского университета. ISBN 978-0-521-57698-7 

Информатика

• Джон Раст Хаббард (2000). Очерк теории и проблем структур данных в Java Шаума , McGraw-Hill. ISBN 978-0-07-137870-3 

Внешние ссылки

• «Геометрическая прогрессия», Математическая энциклопедия , EMS Press , 2001 [1994]
• Вайсштейн, Эрик В. «Геометрическая серия». Математический мир .
• Геометрическая серия в PlanetMath .
• Пеппард, Ким. «Учебник колледжа по алгебре по геометрическим последовательностям и рядам». Университет Западного Техаса A&M.
• Кассельман, Билл. «Геометрическая интерпретация геометрической серии». Архивировано из оригинала (Applet) 29 сентября 2007 г.
• «Геометрическая серия» Михаэля Шрайбера, Демонстрационный проект Wolfram , 2007 г.