Граф Петерсена

Кубический граф с 10 вершинами и 15 ребрами

В математической области теории графов граф Петерсена — это неориентированный граф с 10 вершинами и 15 ребрами . Это небольшой граф, который служит полезным примером и контрпримером для многих задач в теории графов. Граф Петерсена назван в честь Юлиуса Петерсена , который в 1898 году построил его как наименьший кубический граф без мостов без трех -реберной раскраски . ^{[1] [2]}

Хотя граф обычно приписывают Петерсену, на самом деле он впервые появился 12 лет назад в статье AB Kempe  (1886). Kempe заметил, что его вершины могут представлять десять линий конфигурации Дезарга , а его ребра представляют пары линий, которые не встречаются ни в одной из десяти точек конфигурации. ^[3]

Дональд Кнут утверждает, что граф Петерсена — это «замечательная конфигурация, которая служит контрпримером многим оптимистичным прогнозам о том, что может быть верным для графов в целом». ^[4]

Граф Петерсена также появляется в тропической геометрии . Конус над графом Петерсена естественным образом отождествляется с пространством модулей пятиточечных рациональных тропических кривых.

Конструкции

Граф Петерсена как граф Кнезера ${\displaystyle KG_{5,2}}$

Граф Петерсена является дополнением линейного графа . Он также является графом Кнезера ; это означает, что он имеет одну вершину для каждого 2-элементного подмножества 5-элементного множества, и две вершины соединены ребром тогда и только тогда, когда соответствующие 2-элементные подмножества не пересекаются друг с другом. Как граф Кнезера вида он является примером нечетного графа . ${\displaystyle K_{5}}$ ${\displaystyle KG_{5,2}}$ ${\displaystyle KG_{2n-1,n-1}}$

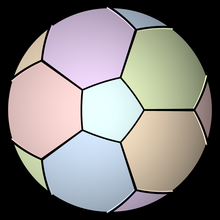
Геометрически граф Петерсена — это граф, образованный вершинами и ребрами полудодекаэдра , то есть додекаэдра , у которого противоположные точки, прямые и грани отождествлены вместе.

Вложения

Граф Петерсена непланарен . Любой непланарный граф имеет в качестве миноров либо полный граф , либо полный двудольный граф , но граф Петерсена имеет оба в качестве миноров. Минор может быть образован стягиванием ребер совершенного паросочетания , например, пяти коротких ребер на первом рисунке. Минор может быть образован удалением одной вершины (например, центральной вершины 3-симметричного рисунка) и стягиванием ребра, инцидентного каждому соседу удаленной вершины. ${\displaystyle K_{5}}$ ${\displaystyle K_{3,3}}$ ${\displaystyle K_{5}}$ ${\displaystyle K_{3,3}}$

Граф Петерсена имеет число пересечений 2 и является 1-планарным .

Наиболее распространенный и симметричный плоский рисунок графа Петерсена, как пентаграмма внутри пентагона, имеет пять пересечений. Однако это не лучший рисунок для минимизации пересечений; существует другой рисунок (показанный на рисунке) только с двумя пересечениями. Поскольку он непланарный, он имеет по крайней мере одно пересечение в любом рисунке, и если ребро пересечения удалить из любого рисунка, он остается непланарным и имеет другое пересечение; поэтому его число пересечений равно ровно 2. Каждое ребро в этом рисунке пересекается не более одного раза, поэтому граф Петерсена является 1-планарным . На торе граф Петерсена можно нарисовать без пересечений ребер; поэтому он имеет ориентируемый род 1.

Граф Петерсена представляет собой граф единичных расстояний : его можно изобразить на плоскости, где каждое ребро имеет единичную длину.

Граф Петерсена можно также нарисовать (с пересечениями) на плоскости таким образом, чтобы все ребра имели одинаковую длину. То есть это граф единичных расстояний .

Простейшей неориентируемой поверхностью , на которой граф Петерсена может быть вложен без пересечений, является проективная плоскость . Это вложение, заданное конструкцией полудодекаэдра графа Петерсена (показано на рисунке). Вложение проективной плоскости также может быть сформировано из стандартного пятиугольного рисунка графа Петерсена путем помещения крестообразной крышки в пятиконечную звезду в центре рисунка и прокладывания ребер звезды через эту крестообразную крышку; полученный рисунок имеет шесть пятиугольных граней. Эта конструкция образует регулярную карту и показывает, что граф Петерсена имеет неориентируемый род 1.

Граф Петерсена и связанная с ним карта, вложенная в проективную плоскость . Противоположные точки на окружности определяются, что дает замкнутую поверхность неориентируемого рода 1.

Симметрии

Граф Петерсена строго регулярен (с сигнатурой srg(10,3,0,1)). Он также симметричен , что означает, что он транзитивен по ребрам и вершинам . Более того, он 3-дугово-транзитивен: каждый направленный путь из трех ребер в графе Петерсена может быть преобразован в любой другой такой путь с помощью симметрии графа. ^[5] Это один из всего лишь 13 кубических дистанционно-регулярных графов . ^[6]

Группа автоморфизмов графа Петерсена — это симметрическая группа ; действие на граф Петерсена следует из его построения как графа Кнезера . Граф Петерсена — это ядро : каждый гомоморфизм графа Петерсена в себя является автоморфизмом . [ ^7] Как показано на рисунках, рисунки графа Петерсена могут демонстрировать пятистороннюю или трехстороннюю симметрию, но невозможно нарисовать граф Петерсена на плоскости таким образом, чтобы рисунок демонстрировал полную группу симметрии графа. ${\displaystyle S_{5}}$ ${\displaystyle S_{5}}$

Несмотря на высокую степень симметрии, граф Петерсена не является графом Кэли . Это наименьший вершинно-транзитивный граф, который не является графом Кэли. ^[a]

Гамильтоновы пути и циклы

Граф Петерсена является гипогамильтоновым: при удалении любой вершины, например центральной вершины на рисунке, оставшийся граф является гамильтоновым. Этот рисунок с симметрией порядка 3 — тот, что дал Кемпе (1886).

Граф Петерсена имеет гамильтонов путь , но не имеет гамильтонова цикла . Это наименьший кубический граф без мостов, не имеющий гамильтонова цикла. Он является гипогамильтоновым , что означает, что, хотя у него нет гамильтонова цикла, удаление любой вершины делает его гамильтоновым, и это наименьший гипогамильтонов граф.

Как конечный связный вершинно-транзитивный граф, не имеющий гамильтонова цикла, граф Петерсена является контрпримером к варианту гипотезы Ловаса , но каноническая формулировка гипотезы требует гамильтонова пути и подтверждается графом Петерсена.

Известно всего пять связных вершинно-транзитивных графов без гамильтоновых циклов: полный граф K2 , граф Петерсена, граф Коксетера и два графа, полученные из графов Петерсена и Коксетера путем замены каждой вершины треугольником. ^[6] Если G является ₂ -связным, r -регулярным графом с не более чем 3 r  + 1 вершинами, то G является гамильтоновым или G является графом Петерсена. ^[8]

Чтобы увидеть, что граф Петерсена не имеет гамильтонова цикла, рассмотрим ребра в разрезе, отделяющем внутренний 5-цикл от внешнего. Если есть гамильтонов цикл C , он должен содержать четное число этих ребер. Если он содержит только два из них, их конечные вершины должны быть смежными в двух 5-циклах, что невозможно. Следовательно, он содержит ровно четыре из них. Предположим, что верхнее ребро разреза не содержится в C (все остальные случаи одинаковы по симметрии). Из пяти ребер во внешнем цикле два верхних ребра должны быть в C , два боковых ребра не должны быть в C , и, следовательно, нижнее ребро должно быть в C . Два верхних ребра во внутреннем цикле должны быть в C , но это завершает неостовной цикл, который не может быть частью гамильтонова цикла. В качестве альтернативы мы также можем описать 3-регулярные графы с десятью вершинами , которые имеют гамильтонов цикл, и показать, что ни один из них не является графом Петерсена, найдя цикл в каждом из них, который короче любого цикла в графе Петерсена. Любой гамильтонов 3-регулярный граф с десятью вершинами состоит из цикла C с десятью вершинами и пяти хорд. Если любая хорда соединяет две вершины на расстоянии двух или трех вдоль C друг от друга, граф имеет 3-цикл или 4-цикл и, следовательно, не может быть графом Петерсена. Если две хорды соединяют противоположные вершины C с вершинами на расстоянии четырех вдоль C , снова есть 4-цикл. Единственный оставшийся случай — это лестница Мёбиуса , образованная путем соединения каждой пары противоположных вершин хордой, которая снова имеет 4-цикл. Поскольку граф Петерсена имеет обхват пять, он не может быть образован таким образом и не имеет гамильтонова цикла.

Раскрашивание

Четырехцветная раскраска ребер графа Петерсена

3-х цветная раскраска вершин графа Петерсена

Граф Петерсена имеет хроматическое число 3, что означает, что его вершины могут быть окрашены тремя цветами — но не двумя — так, что ни одно ребро не соединяет вершины одного цвета. Он имеет списочную раскраску с 3 цветами, по теореме Брукса для списочных раскрасок.

Граф Петерсена имеет хроматический индекс 4; для раскраски ребер требуется четыре цвета. Как связный кубический граф без мостов с хроматическим индексом четыре, граф Петерсена является снарком . Это наименьший возможный снарком, и был единственным известным снарком с 1898 по 1946 год. Теорема о снарке , результат, выдвинутый У. Т. Туттом и объявленный в 2001 году Робертсоном, Сандерсом, Сеймуром и Томасом, ^[9] утверждает, что каждый снарком имеет граф Петерсена в качестве минора .

Кроме того, граф имеет дробный хроматический индекс 3, что доказывает, что разница между хроматическим индексом и дробным хроматическим индексом может достигать 1. Давняя гипотеза Голдберга-Сеймура предполагает, что это максимально возможный разрыв.

Число Туэ (вариант хроматического индекса) графа Петерсена равно 5.

Граф Петерсена требует по крайней мере три цвета в любой (возможно, неправильной) раскраске, которая нарушает все его симметрии; то есть его отличительное число равно трем. За исключением полных графов, это единственный граф Кнезера, отличительное число которого не равно двум. ^[10]

Другие свойства

График Петерсена:

• является 3-связным и, следовательно, 3-рёберно-связным и без мостов. См. глоссарий .
• имеет число независимости 4 и является 3-частным. См. глоссарий .
• является кубическим , имеет доминирующее число 3, имеет идеальное паросочетание и 2-фактор .
• имеет 6 различных идеальных паросочетаний.
• является наименьшим кубическим графом обхвата 5. (Это уникальный - клетка . Фактически, поскольку он имеет только 10 вершин, это уникальный - граф Мура .) ^[11] ${\displaystyle (3,5)}$ ${\displaystyle (3,5)}$
• каждый кубический граф без мостов без минора Петерсена имеет циклическое двойное покрытие. ^[12]
• является наименьшим кубическим графом с инвариантом графа Колина де Вердьера μ = 5. ^[13]
• это наименьший граф полицейского номер 3. ^[14]
• имеет радиус 2 и диаметр 2. Это самый большой кубический граф с диаметром 2. ^[b]
• имеет 2000 остовных деревьев , больше, чем любой кубический граф с 10 вершинами. ^{[15] [16] [c]}
• имеет хроматический многочлен . ^[17] ${\displaystyle t(t-1)(t-2)\left(t^{7}-12t^{6}+67t^{5}-230t^{4}+529t^{3}-814t^{2}+775t-352\right)}$
• имеет характеристический многочлен , что делает его целочисленным графом — графом, спектр которого состоит исключительно из целых чисел. ${\displaystyle (t-1)^{5}(t+2)^{4}(t-3)}$

гипотеза Петерсена о раскраске

Эйлеров подграф графа — это подграф, состоящий из подмножества ребер , касающихся каждой вершины четное число раз. Эти подграфы являются элементами пространства циклов и иногда называются циклами. Если и — любые два графа, функция от ребер до ребер определяется как непрерывная по циклам, если прообраз каждого цикла является циклом . Гипотеза Йегера утверждает, что каждый граф без мостов имеет непрерывное по циклам отображение на граф Петерсена. Йегер показал, что эта гипотеза влечет гипотезу о двойном покрытии 5 циклов и гипотезу Берже-Фалкерсона." ^[18] ${\displaystyle G}$ ${\displaystyle G}$ ${\displaystyle G}$ ${\displaystyle G}$ ${\displaystyle G}$ ${\displaystyle H}$ ${\displaystyle G}$ ${\displaystyle H}$ ${\displaystyle H}$ ${\displaystyle G}$

Связанные графики

Семья Петерсен .

Обобщенный граф Петерсена образуется путем соединения вершин правильного n- угольника с соответствующими вершинами звездчатого многоугольника с символом Шлефли { n / k }. ^{[19] [20]} Например, в этой нотации граф Петерсена имеет вид : он может быть образован путем соединения соответствующих вершин пятиугольника и пятиконечной звезды, а ребра в звезде соединяют каждую вторую вершину. Обобщенные графы Петерсена также включают n -призму , граф Дюрера , граф Мёбиуса-Кантора , додекаэдр , граф Дезарга и граф Науру . ${\displaystyle G(n,k)}$ ${\displaystyle G(5,2)}$ ${\displaystyle G(n,1)}$ ${\displaystyle G(6,2)}$ ${\displaystyle G(8,3)}$ ${\displaystyle G(10,2)}$ ${\displaystyle G(10,3)}$ ${\displaystyle G(12,5)}$

Семейство Петерсена состоит из семи графов, которые могут быть сформированы из графа Петерсена нулем или более применений преобразований Δ-Y или Y-Δ . Полный граф K ₆ также принадлежит семейству Петерсена. Эти графы образуют запрещенные миноры для графов, вкладываемых без зацепления , графов, которые могут быть вложены в трехмерное пространство таким образом, что никакие два цикла в графе не связаны . ^[21]

Граф Клебша содержит множество копий графа Петерсена в качестве индуцированных подграфов : для каждой вершины v графа Клебша десять вершин, не являющихся соседями v, индуцируют копию графа Петерсена.

Примечания

1. Как указано, это предполагает, что графы Кэли не обязательно должны быть связными. Некоторые источники требуют, чтобы графы Кэли были связными, делая пустой граф с двумя вершинами наименьшим вершинно-транзитивным графом, не являющимся графом Кэли; согласно определению, данному этими источниками, граф Петерсена является наименьшим связным вершинно-транзитивным графом, не являющимся графом Кэли.
2. Это следует из того факта, что это граф Мура, поскольку любой граф Мура является наибольшим возможным регулярным графом с его степенью и диаметром. ^[11]
3. Кубические графы с 6 и 8 вершинами, максимизирующие число остовных деревьев, являются лестницами Мёбиуса .

Ссылки

1. Брауэр, Андрис Э. , Граф Петерсена
2. Петерсен, Юлиус (1898), "Sur le theorème de Tait", L'Intermédiaire des Mathématiciens , 5 : 225–227
3. Кемпе, AB (1886), «Мемуары по теории математической формы», Philosophical Transactions of the Royal Society of London , 177 : 1–70, doi : 10.1098/rstl.1886.0002, S2CID  108716533
4. Кнут, Дональд Э., Искусство программирования; том 4, предыстория 0A. Черновик раздела 7: Введение в комбинаторный поиск
5. Бабай, Ласло (1995), «Группы автоморфизмов, изоморфизм, реконструкция», в Грэме, Рональде Л .; Гретшель, Мартин ; Ловаш, Ласло (ред.), Справочник по комбинаторике, том. I, Северная Голландия, стр. 1447–1540, Следствие 1.8, заархивировано из оригинала 11 июня 2010 г..
6. Royle, G. "Cubic Symmetric Graphs (The Foster Census)". Архивировано 20 июля 2008 г. на Wayback Machine
7. Кэмерон, Питер Дж. (2004), «Автоморфизмы графов», в Бейнеке, Лоуэлл У.; Уилсон, Робин Дж. (ред.), Топики алгебраической теории графов , Энциклопедия математики и ее приложений, т. 102, Cambridge University Press, Кембридж, стр. 135–153, doi :10.1017/CBO9780511529993, ISBN 0-521-80197-4, МР  2125091; см. в частности стр. 153
8. Холтон, ДА; Шихан, Дж. (1993), График Петерсена , Cambridge University Press , стр. 32, ISBN 0-521-43594-3
9. Пегг, Эд младший (2002), «Обзор книги: Колоссальная книга математики» (PDF) , Notices of the American Mathematical Society , 49 (9): 1084–1086, Bibcode : 2002ITED...49.1084A, doi : 10.1109/TED.2002.1003756
10. Альбертсон, Майкл О.; Бутин, Дебра Л. (2007), «Использование определяющих множеств для различения графов Кнезера», Электронный журнал комбинаторики , 14 (1): R20, doi : 10.37236/938 , MR  2285824.
11. Хоффман, Алан Дж.; Синглтон, Роберт Р. (1960), «Графы Мура с диаметром 2 и 3» (PDF) , IBM Journal of Research and Development , 5 (4): 497–504, doi :10.1147/rd.45.0497, MR  0140437.
12. Alspach, Brian; Zhang, Cun-Quan (1993), «Цикловые покрытия кубических мультиграфов», Discrete Math. , 111 (1–3): 11–17, doi :10.1016/0012-365X(93)90135-G.
13. Ласло Ловас, Александр Шрайвер (1998), «Теорема Борсука для антиподальных связей и спектральная характеристика графов, вкладываемых без связей» (PDF) , Труды Американского математического общества , 126 (5): 1275–1285, doi :10.1090/S0002-9939-98-04244-0, S2CID  7790459
14. Бэрд, Уильям; Беверидж, Эндрю; Бонато, Энтони; Коденотти, Паоло; Маурер, Аарон; Макколи, Джон; Валева, Сильвия (2014), «О минимальном порядке графов k-cop-win», Вклад в дискретную математику , 9 (1): 70–84, arXiv : 1308.2841 , doi : 10.11575/cdm.v9i1.62207 , MR  3265753
15. Якобсон, Дмитрий; Ривин, Игорь (1999), О некоторых экстремальных задачах в теории графов , arXiv : math.CO/9907050 , Bibcode : 1999math......7050J
16. Вальдес, Л. (1991), «Экстремальные свойства остовных деревьев в кубических графах», Congressus Numerantium , 85 : 143–160.
17. Биггс, Норман (1993), Алгебраическая теория графов (2-е изд.), Кембридж: Cambridge University Press, ISBN 0-521-45897-8
18. ДеВос, Мэтт; Нешетржил, Ярослав ; Распо, Андре (2007), «О рёберных картах, обратные которым сохраняют потоки или напряжения», Теория графов в Париже , Trends Math., Базель: Birkhäuser, стр. 109–138, doi :10.1007/978-3-7643-7400-6_10, ISBN 978-3-7643-7228-6, г-н  2279171.
19. Коксетер, HSM (1950), «Самодвойственные конфигурации и регулярные графы», Бюллетень Американского математического общества , 56 (5): 413–455, doi : 10.1090/S0002-9904-1950-09407-5.
20. Уоткинс, Марк Э. (1969), «Теорема о раскрасках Тейта с приложением к обобщенным графам Петерсена», Журнал комбинаторной теории , 6 (2): 152–164, doi : 10.1016/S0021-9800(69)80116-X
21. Бейли, Розмари А. (1997), Обзоры комбинаторики , Cambridge University Press, стр. 187, ISBN 978-0-521-59840-8

Дальнейшее чтение

• Эксо, Джеффри; Харари, Фрэнк ; Кабелл, Джеральд (1981), «Числа пересечений некоторых обобщенных графов Петерсена», Mathematica Scandinavica , 48 : 184–188, doi : 10.7146/math.scand.a-11910.
• Ловас, Ласло (1993), Комбинаторные задачи и упражнения (2-е изд.), Северная Голландия, ISBN 0-444-81504-X.
• Швенк, А. Дж. (1989), «Перечисление гамильтоновых циклов в некоторых обобщенных графах Петерсена», Журнал комбинаторной теории , Серия B, 47 (1): 53–59, doi : 10.1016/0095-8956(89)90064-6
• Чжан, Цунь-Цюань (1997), Целочисленные потоки и циклические покрытия графов , CRC Press, ISBN 978-0-8247-9790-4.
• Чжан, Цунь-Цюань (2012), Circuit Double Cover of Graphs , Cambridge University Press, ISBN 978-0-5212-8235-2.

Внешние ссылки

• Вайсштейн, Эрик В. , «График Петерсена», MathWorld
• Граф Петерсена в онлайн-энциклопедии целочисленных последовательностей