Детерминированный конечный автомат

Конечный автомат

Пример детерминированного конечного автомата, который принимает только двоичные числа, кратные 3. Состояние S ₀ является как начальным состоянием, так и состоянием принятия. Например, строка "1001" приводит к последовательности состояний S ₀ , S ₁ , S ₂ , S ₁ , S ₀ и, следовательно, принимается.

В теории вычислений , разделе теоретической информатики , детерминированный конечный автомат ( DFA ) — также известный как детерминированный конечный акцептор ( DFA ), детерминированный конечный автомат ( DFSM ) или детерминированный конечный автомат ( DFSA ) — это конечный автомат , который принимает или отклоняет заданную строку символов, проходя через последовательность состояний, однозначно определяемую строкой. ^[1] Детерминированный относится к уникальности вычислительного цикла. В поисках простейших моделей для захвата конечных автоматов Уоррен Маккалок и Уолтер Питтс были среди первых исследователей, которые ввели концепцию, похожую на конечный автомат, в 1943 году. ^{[2] [3]}

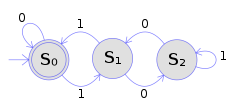
На рисунке показан детерминированный конечный автомат с использованием диаграммы состояний . В этом примере автомата есть три состояния: S ₀ , S ₁ и S ₂ (графически обозначены кружками). Автомат принимает конечную последовательность нулей и единиц в качестве входных данных. Для каждого состояния есть стрелка перехода, ведущая к следующему состоянию как для 0, так и для 1. При считывании символа DFA детерминированно переходит из одного состояния в другое, следуя стрелке перехода. Например, если автомат в данный момент находится в состоянии S ₀ , а текущий входной символ равен 1, то он детерминированно переходит в состояние S ₁ . DFA имеет начальное состояние (графически обозначенное стрелкой, входящей из ниоткуда), в котором начинаются вычисления, и набор состояний принятия (графически обозначенных двойным кружком), которые помогают определить, когда вычисление успешно.

DFA определяется как абстрактная математическая концепция, но часто реализуется в аппаратном и программном обеспечении для решения различных конкретных задач, таких как лексический анализ и сопоставление с образцом . Например, DFA может моделировать программное обеспечение, которое решает, является ли ввод данных пользователем в режиме онлайн, например, адреса электронной почты, синтаксически допустимым. ^[4]

DFA были обобщены до недетерминированных конечных автоматов (NFA) , которые могут иметь несколько стрелок с одинаковой меткой, начинающихся из состояния. Используя метод построения powerset , каждый NFA может быть переведен в DFA, который распознает тот же язык. DFA, а также NFA, распознают в точности множество регулярных языков . ^[1]

Формальное определение

Детерминированный конечный автомат M — это 5- кортеж ( Q , Σ, δ , q ₀ , F ) , состоящий из

• конечный набор состояний Q
• конечный набор входных символов, называемый алфавитом Σ
• функция перехода δ  : Q × Σ → Q
• начальное или стартовое состояние ${\displaystyle q_{0}\in Q}$
• набор состояний принятия ${\displaystyle F\subseteq Q}$

Пусть w = a ₁ a ₂ ... a _n будет строкой над алфавитом Σ . Автомат M принимает строку w, если последовательность состояний r ₀ , r ₁ , ..., r _n существует в Q со следующими условиями:

1. р ₀ = q ₀
2. r _{i +1} = δ ( r _i , a _{i +1} ) , для i = 0, ..., n − 1
3. ${\displaystyle r_{n}\in F}$.

На словах первое условие говорит, что машина начинает работу в начальном состоянии q ₀ . Второе условие говорит, что при каждом символе строки w машина будет переходить из состояния в состояние в соответствии с функцией перехода δ . Последнее условие говорит, что машина принимает w, если последний ввод w заставляет машину остановиться в одном из принимающих состояний. В противном случае говорят, что автомат отвергает строку. Набор строк, которые принимает M, — это язык, распознаваемый M , и этот язык обозначается как L ( M ) .

Детерминированный конечный автомат без допустимых состояний и без начального состояния известен как система переходов или полуавтомат .

Более полное введение в формальное определение см. в статье Теория автоматов .

Пример

Следующий пример представляет собой DFA M с двоичным алфавитом, который требует, чтобы входные данные содержали четное число нулей.

Диаграмма состояний для M

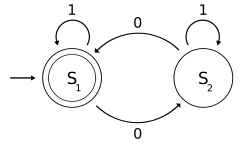
M = ( Q , Σ, δ , q ₀ , F ) где

• Q ₌ { С1 , С2 }_​
• Σ = {0, 1}
• q0 = S1_​​
• Ф = { С ₁ } и
• δ определяется следующей таблицей переходов состояний :

Состояние S ₁ означает, что на входе было четное число нулей, а S ₂ означает нечетное число. 1 на входе не изменяет состояние автомата. Когда вход заканчивается, состояние покажет, содержал ли вход четное число нулей или нет. Если вход содержал четное число нулей, M завершит работу в состоянии S ₁ , принимающем состоянии, поэтому входная строка будет принята.

Язык, распознаваемый M, — это регулярный язык , заданный регулярным выражением (1*) (0 (1*) 0 (1*))* , где *— звезда Клини , например, 1*обозначает любое количество (возможно, ноль) последовательных единиц.

Вариации

Полные и неполные

Согласно приведенному выше определению, детерминированные конечные автоматы всегда полны : они определяют из каждого состояния переход для каждого входного символа.

Хотя это наиболее распространенное определение, некоторые авторы используют термин детерминированный конечный автомат для несколько иного понятия: автомата, который определяет не более одного перехода для каждого состояния и каждого входного символа; функция перехода может быть частичной . ^[5] Если переход не определен, такой автомат останавливается.

Локальные автоматы

Локальный автомат — это DFA, не обязательно полный, для которого все ребра с одинаковой меткой ведут к одной вершине. Локальные автоматы принимают класс локальных языков , тех, для которых принадлежность слова к языку определяется «скользящим окном» длины два на слове. ^{[6] [7]}

Граф Myhill над алфавитом A — это направленный граф с множеством вершин A и подмножествами вершин, помеченными как «старт» и «финиш». Язык, принимаемый графом Myhill, — это набор направленных путей от начальной вершины до конечной вершины: таким образом, граф действует как автомат. ^[6] Класс языков, принимаемых графами Myhill, — это класс локальных языков. ^[8]

Случайность

Когда начальное состояние и состояния принятия игнорируются, DFA из n состояний и алфавита размера k можно рассматривать как орграф из n вершин, в котором все вершины имеют k исходящих дуг, помеченных 1, ..., k ( орграф с k -выходом). Известно, что когда k ≥ 2 является фиксированным целым числом, с высокой вероятностью наибольший сильно связанный компонент (SCC) в таком орграфе с k -выходом, выбранный равномерно случайным образом, имеет линейный размер и может быть достигнут всеми вершинами. ^[9] Также было доказано, что если k разрешено увеличиваться с ростом n , то весь орграф имеет фазовый переход для сильной связности, аналогичный модели Эрдёша–Реньи для связности. ^[10]

В случайном DFA максимальное количество вершин, достижимых из одной вершины, очень близко к количеству вершин в наибольшем SCC с высокой вероятностью. ^{[9] [11]} Это также верно для наибольшего индуцированного под-орграфа с минимальной входящей степенью один, который можно рассматривать как направленную версию 1 -ядра . ^[10]

Свойства закрытия

Верхний левый автомат распознает язык всех двоичных строк, содержащих хотя бы одно вхождение «00». Нижний правый автомат распознает все двоичные строки с четным числом «1». Нижний левый автомат получается как произведение первых двух, он распознает пересечение обоих языков.

Если DFA распознают языки, которые получены путем применения операции к языкам, распознаваемым DFA, то говорят, что DFA закрыты относительно операции. DFA закрыты относительно следующих операций.

• Союз
• Пересечение ^{[12] : 59–60} (см. рисунок)
• Конкатенация
• Дополнение
• закрытие Клини
• Обратный ход ^[13]
• Коэффициент ^[13]
• Замена ^[14]
• Гомоморфизм ^{[13] [14]}

Для каждой операции оптимальная конструкция относительно числа состояний была определена в исследовании сложности состояний . Поскольку DFA эквивалентны недетерминированным конечным автоматам (NFA), эти замыкания также могут быть доказаны с использованием свойств замыкания NFA.

Как переходный моноид

Прогон данного DFA можно рассматривать как последовательность композиций очень общей формулировки функции перехода с собой. Здесь мы строим эту функцию.

Для заданного входного символа можно построить функцию перехода , определив для всех . (Этот трюк называется каррированием .) С этой точки зрения, «действует» на состояние в Q, чтобы получить другое состояние. Затем можно рассмотреть результат композиции функций, многократно примененной к различным функциям , , и так далее. Учитывая пару букв , можно определить новую функцию , где обозначает композицию функций. ${\displaystyle a\in \Sigma }$ ${\displaystyle \delta _{a}:Q\rightarrow Q}$ ${\displaystyle \delta _{a}(q)=\delta (q,a)}$ ${\displaystyle q\in Q}$ ${\displaystyle \delta _{a}}$ ${\displaystyle \delta _{a}}$ ${\displaystyle \delta _{b}}$ ${\displaystyle a,b\in \Sigma }$ ${\displaystyle {\widehat {\delta }}_{ab}=\delta _{a}\circ \delta _{b}}$ ${\displaystyle \circ }$

Очевидно, этот процесс можно рекурсивно продолжить, дав следующее рекурсивное определение : ${\displaystyle {\widehat {\delta }}:Q\times \Sigma ^{\star }\rightarrow Q}$

${\displaystyle {\widehat {\delta }}(q,\epsilon )=q}$, где пустая строка и ${\displaystyle \epsilon }$

${\displaystyle {\widehat {\delta }}(q,wa)=\delta _{a}({\widehat {\delta }}(q,w))}$, где и . ${\displaystyle w\in \Sigma ^{*},a\in \Sigma }$ ${\displaystyle q\in Q}$

${\displaystyle {\widehat {\delta }}}$ определено для всех слов . Прогон DFA представляет собой последовательность композиций с самим собой. ${\displaystyle w\in \Sigma ^{*}}$ ${\displaystyle {\widehat {\delta }}}$

Повторная композиция функций образует моноид . Для функций перехода этот моноид известен как моноид перехода или иногда полугруппа преобразований . Построение также может быть обратным: если задано a , можно реконструировать a , и поэтому два описания эквивалентны. ${\displaystyle {\widehat {\delta }}}$ ${\displaystyle \delta }$

Преимущества и недостатки

DFA являются одной из наиболее практичных моделей вычислений, поскольку существует тривиальный линейный по времени, постоянный по пространству, онлайн-алгоритм для моделирования DFA на потоке входных данных. Кроме того, существуют эффективные алгоритмы для поиска DFA, распознающего:

• дополнение к языку, распознаваемому данным DFA.
• объединение/пересечение языков, распознаваемых двумя заданными DFA.

Поскольку DFA можно свести к канонической форме ( минимальные DFA ), существуют также эффективные алгоритмы для определения:

• принимает ли DFA какие-либо строки (проблема пустоты)
• принимает ли DFA все строки (проблема универсальности)
• распознают ли два DFA один и тот же язык (проблема равенства)
• включен ли язык, распознаваемый DFA, в язык, распознаваемый вторым DFA (проблема включения)
• DFA с минимальным числом состояний для конкретного регулярного языка (задача минимизации)

DFA эквивалентны по вычислительной мощности недетерминированным конечным автоматам (NFA). Это связано с тем, что, во-первых, любой DFA также является NFA, поэтому NFA может делать то, что может делать DFA. Кроме того, имея NFA, используя конструкцию powerset, можно построить DFA, который распознает тот же язык, что и NFA, хотя DFA может иметь экспоненциально большее количество состояний, чем NFA. ^{[15] [16]} Однако, даже несмотря на то, что NFA вычислительно эквивалентны DFA, вышеупомянутые проблемы не обязательно решаются эффективно также для NFA. Проблема неуниверсальности для NFA является PSPACE-полной , поскольку существуют небольшие NFA с кратчайшим отвергающим словом в экспоненциальном размере. DFA является универсальным тогда и только тогда, когда все состояния являются конечными, но это не выполняется для NFA. Проблемы равенства, включения и минимизации также являются PSPACE-полными, поскольку они требуют формирования дополнения NFA, что приводит к экспоненциальному увеличению размера. ^[17]

С другой стороны, конечные автоматы имеют строго ограниченную мощность в языках, которые они могут распознавать; многие простые языки, включая любую задачу, требующую больше, чем константное пространство для решения, не могут быть распознаны DFA. Классический пример просто описанного языка, который не может распознать ни один DFA, это язык скобок или язык Дика , т. е. язык, состоящий из правильно парных скобок, таких как слово "(()())". Интуитивно, ни один DFA не может распознать язык Дика, потому что DFA не способны считать: автомат, подобный DFA, должен иметь состояние для представления любого возможного количества "открытых в данный момент" скобок, то есть ему потребуется неограниченное количество состояний. Другим более простым примером является язык, состоящий из строк вида a ⁿ b ⁿ для некоторого конечного, но произвольного количества a ' , за которыми следует равное количество b ' . ^[18]

DFA-идентификация по маркированным словам

Для заданного набора положительных слов и набора отрицательных слов можно построить DFA, который принимает все слова из и отклоняет все слова из : эта задача называется идентификацией DFA (синтез, обучение). Хотя некоторые DFA могут быть построены за линейное время, задача идентификации DFA с минимальным числом состояний является NP-полной. ^[19] Первый алгоритм для минимальной идентификации DFA был предложен Трахтенбротом и Барздином ^[20] и называется TB-алгоритмом . Однако TB-алгоритм предполагает, что все слова из до заданной длины содержатся либо в . ${\displaystyle S^{+}\subset \Sigma ^{*}}$ ${\displaystyle S^{-}\subset \Sigma ^{*}}$ ${\displaystyle S^{+}}$ ${\displaystyle S^{-}}$ ${\displaystyle \Sigma }$ ${\displaystyle S^{+}\cup S^{-}}$

Позднее К. Ланг предложил расширение TB-алгоритма, не использующее никаких предположений о и , алгоритм Traxbar . ^[21] Однако Traxbar не гарантирует минимальность построенного DFA. В своей работе ^[19] Э. М. Голд также предложил эвристический алгоритм для минимальной идентификации DFA. Алгоритм Голда предполагает, что и содержат характеристический набор регулярного языка; в противном случае построенный DFA будет несовместим либо с , либо . Другие известные алгоритмы идентификации DFA включают алгоритм RPNI, ^[22] алгоритм слияния состояний на основе доказательств Blue-Fringe ^[23] и Windowed-EDSM. ^[24] Другое направление исследований — применение эволюционных алгоритмов : эволюционный алгоритм интеллектуальной маркировки состояний ^[25] позволил решить модифицированную задачу идентификации DFA, в которой обучающие данные (наборы и ) являются зашумленными в том смысле, что некоторые слова отнесены к неправильным классам. ${\displaystyle S^{+}}$ ${\displaystyle S^{-}}$ ${\displaystyle S^{+}}$ ${\displaystyle S^{-}}$ ${\displaystyle S^{+}}$ ${\displaystyle S^{-}}$ ${\displaystyle S^{+}}$ ${\displaystyle S^{-}}$

Еще один шаг вперед связан с применением решателей SAT Марджином Дж. Х. Хойлом и С. Вервером: проблема идентификации минимального DFA сводится к решению выполнимости булевой формулы. ^[26] Основная идея состоит в том, чтобы построить акцептор расширенного префиксного дерева ( trie, содержащий все входные слова с соответствующими метками) на основе входных наборов и свести задачу поиска DFA с состояниями к раскрашиванию вершин дерева с состояниями таким образом, чтобы при объединении вершин с одним цветом в одно состояние сгенерированный автомат был детерминированным и соответствовал и . Хотя этот подход позволяет найти минимальный DFA, он страдает от экспоненциального раздувания времени выполнения при увеличении размера входных данных. Поэтому первоначальный алгоритм Хойла и Вервера позже был дополнен несколькими шагами алгоритма EDSM перед выполнением решателя SAT: алгоритм DFASAT. ^[27] Это позволяет сократить пространство поиска задачи, но приводит к потере гарантии минимальности. Другой способ сокращения пространства поиска был предложен Ульянцевым и др. ^[28] с помощью новых предикатов нарушения симметрии, основанных на алгоритме поиска в ширину : искомые состояния DFA ограничены нумерацией в соответствии с алгоритмом BFS, запущенным из начального состояния. Такой подход сокращает пространство поиска за счет исключения изоморфных автоматов. ${\displaystyle C}$ ${\displaystyle C}$ ${\displaystyle S^{+}}$ ${\displaystyle S^{-}}$ ${\displaystyle C!}$

Эквивалентные модели

Машины Тьюринга, работающие только на чтение и движущиеся вправо

Машины Тьюринга, движущиеся только вправо и только для чтения, являются особым типом машины Тьюринга , которая движется только вправо; они почти полностью эквивалентны DFA. ^[29] Определение, основанное на однократно бесконечной ленте, представляет собой 7- кортеж

${\displaystyle M=\langle Q,\Gamma ,b,\Sigma ,\delta ,q_{0},F\rangle ,}$

где

${\displaystyle Q}$— конечный набор состояний ;

${\displaystyle \Gamma }$представляет собой конечный набор алфавита/символов ленты ;

${\displaystyle b\in \Gamma }$— пустой символ (единственный символ, которому разрешено появляться на ленте бесконечно часто на любом этапе вычислений);

${\displaystyle \Sigma }$, подмножество, не включающее b , представляет собой множество входных символов ; ${\displaystyle \Gamma }$

${\displaystyle \delta :Q\times \Gamma \to Q\times \Gamma \times \{R\}}$— функция, называемая функцией перехода , R — движение вправо (сдвиг вправо);

${\displaystyle q_{0}\in Q}$— начальное состояние ;

${\displaystyle F\subseteq Q}$это набор конечных или принимающих состояний .

Машина всегда принимает регулярный язык. Для того, чтобы язык был непустым, должен существовать хотя бы один элемент множества F ( состояние HALT ).

Пример машины Тьюринга с тремя состояниями и двумя символами, доступной только для чтения

${\displaystyle Q=\{A,B,C,{\text{HALT}}\};}$

${\displaystyle \Gamma =\{0,1\};}$

${\displaystyle b=0}$, "пустой";

${\displaystyle \Sigma =\varnothing }$, пустой набор;

${\displaystyle \delta =}$см. таблицу состояний выше;

${\displaystyle q_{0}=A}$, начальное состояние;

${\displaystyle F=}$одноэлементный набор конечных состояний: . ${\displaystyle \{{\text{HALT}}\}}$

Смотрите также

• Детерминированный ациклический конечный автомат
• Минимизация DFA
• Монадическая логика второго порядка
• Строительство силовой установки
• Квантовый конечный автомат
• Проблема разделения слов
• машина Тьюринга
• Двусторонний конечный автомат
• Взвешенный автомат

Примечания

1. Hopcroft 2001
2. Маккалок и Питтс (1943)
3. Рабин и Скотт (1959)
4. Бай, Джина Р.; Кли, Брайан; Шреста, Нишал; Чапман, Карл; Райт, Симон; Столи, Кэтрин Т. (2019). «Изучение инструментов и стратегий, используемых при задачах составления регулярных выражений». В Guéhéneuc, Янн-Гаэль; Хом, Фоутсе; Сарро, Федерика (ред.). Труды 27-й Международной конференции по пониманию программ, ICPC 2019, Монреаль, Квебек, Канада, 25–31 мая 2019 г. IEEE / ACM. стр. 197–208. doi :10.1109/ICPC.2019.00039.
5. Могенсен, Торбен Эгидиус (2011). "Лексический анализ". Введение в проектирование компиляторов . Темы бакалавриата по информатике. Лондон: Springer. стр. 12. doi :10.1007/978-0-85729-829-4_1. ISBN 978-0-85729-828-7.
6. Lawson (2004) стр.129
7. Сакарович (2009) стр.228
8. Лоусон (2004) стр.128
9. Грушо, АА (1973). «Предельные распределения некоторых характеристик случайных автоматных графов». Математические записки Академии наук СССР . 4 : 633–637. doi :10.1007/BF01095785. S2CID  121723743.
10. Cai, Xing Shi; Devroye, Luc (октябрь 2017 г.). «Структура графа детерминированного автомата, выбранного случайным образом». Случайные структуры и алгоритмы . 51 (3): 428–458. arXiv : 1504.06238 . doi : 10.1002/rsa.20707. S2CID  13013344.
11. Carayol, Arnaud; Nicaud, Cyril (февраль 2012). Распределение числа доступных состояний в случайном детерминированном автомате. STACS'12 (29-й симпозиум по теоретическим аспектам компьютерной науки). Т. 14. Париж, Франция. С. 194–205.
12. Джон Э. Хопкрофт и Джеффри Д. Ульман (1979). Введение в теорию автоматов, языки и вычисления . Чтение/MA: Addison-Wesley. ISBN 0-201-02988-X.
13. Rose, Gene F. (1968). «Замыкания, сохраняющие конечность в семействах языков». Журнал компьютерных и системных наук . 2 (2): 148–168. doi :10.1016/S0022-0000(68)80029-7.
14. Spanier, E. (1969). «Грамматики и языки». American Mathematical Monthly . 76 : 335–342. doi :10.1080/00029890.1969.12000214. JSTOR  2316423. MR  0241205.
15. Сакарович (2009) стр.105
16. Лоусон (2004) стр.63
17. Эспарса Эстаун, Франсиско Хавьер; Сикерт, Саломон; Блонден, Майкл (16 ноября 2016 г.). «Операции и тесты на множествах: реализация на DFA» (PDF) . Автоматы и формальные языки 2017/18 . Архивировано из оригинала (PDF) 8 августа 2018 г.
18. Лоусон (2004) стр.46
19. Gold, EM (1978). «Сложность идентификации автомата по заданным данным». Информация и управление . 37 (3): 302–320. doi :10.1016/S0019-9958(78)90562-4.
20. Де Врис, А. (28 июня 2014 г.). Конечные автоматы: поведение и синтез. Elsevier. ISBN 9781483297293.
21. Лэнг, Кевин Дж. (1992). «Случайные DFA могут быть приблизительно изучены из разреженных однородных примеров». Труды пятого ежегодного семинара по теории вычислительного обучения — COLT '92 . стр. 45–52. doi :10.1145/130385.130390. ISBN 089791497X. S2CID  7480497.
22. Онсина, Дж.; Гарсия, П. (1992). «Вывод регулярных языков за полиномиальное обновленное время». Распознавание образов и анализ изображений . Серия по машинному восприятию и искусственному интеллекту. Том 1. стр. 49–61. doi :10.1142/9789812797902_0004. ISBN 978-981-02-0881-3.
23. Лэнг, Кевин Дж.; Перлмуттер, Барак А.; Прайс, Родни А. (1998). "Результаты конкурса обучения Abbadingo one DFA и новый алгоритм слияния состояний на основе доказательств". Грамматический вывод (PDF) . Конспект лекций по информатике. Том 1433. С. 1–12. doi :10.1007/BFb0054059. ISBN 978-3-540-64776-8.
24. Beyond EDSM | Труды 6-го Международного коллоквиума по грамматическому выводу: алгоритмы и приложения. 23 сентября 2002 г. С. 37–48. ISBN 9783540442394.
25. Лукас, SM; Рейнольдс, TJ (2005). «Обучение детерминированных конечных автоматов с помощью интеллектуального эволюционного алгоритма маркировки состояний». Труды IEEE по анализу шаблонов и машинному интеллекту . 27 (7): 1063–1074. doi :10.1109/TPAMI.2005.143. PMID  16013754. S2CID  14062047.
26. Heule, MJH (2010). "Exact DFA Identification Using SAT Solvers". Грамматический вывод: теоретические результаты и приложения . Грамматический вывод: теоретические результаты и приложения. ICGI 2010. Lecture Notes in Computer Science. Lecture Notes in Computer Science. Vol. 6339. pp. 66–79. doi :10.1007/978-3-642-15488-1_7. ISBN 978-3-642-15487-4.
27. Heule, Marijn JH ; Verwer, Sicco (2013). «Синтез программной модели с использованием решателей выполнимости». Empirical Software Engineering . 18 (4): 825–856. doi :10.1007/s10664-012-9222-z. hdl : 2066/103766 . S2CID  17865020.
28. Ульянцев, Владимир; Закирзянов, Илья; Шалыто, Анатолий (2015). "BFS-Based Symmetry Breaking Predicates for DFA Identification". Language and Automata Theory and Applications . Lecture Notes in Computer Science. Vol. 8977. pp. 611–622. doi :10.1007/978-3-319-15579-1_48. ISBN 978-3-319-15578-4.
29. Дэвис, Мартин; Рон Сигал; Элейн Дж. Вейукер (1994). Второе издание: Вычислимость, сложность, языки и логика: основы теоретической информатики (2-е изд.). Сан-Диего: Academic Press, Harcourt, Brace & Company. ISBN 0-12-206382-1.

Ссылки

• Хопкрофт, Джон Э .; Мотвани, Раджив ; Ульман, Джеффри Д. (2001). Введение в теорию автоматов, языки и вычисления (2-е изд.). Бостон: Addison Wesley . ISBN 0-201-44124-1.
• Лоусон, Марк В. (2004). Конечные автоматы . Чепмен и Холл/CRC. ISBN 1-58488-255-7. Збл  1086.68074.
• Маккалок, WS; Питтс, W. (1943). «Логическое исчисление идей, имманентных нервной деятельности». Бюллетень математической биофизики . 5 (4): 115–133. doi :10.1007/BF02478259. PMID  2185863.
• Рабин, МО; Скотт, Д. (1959). «Конечные автоматы и их проблемы принятия решений». IBM J. Res. Dev . 3 (2): 114–125. doi :10.1147/rd.32.0114.
• Сакарович, Жак (2009). Элементы теории автоматов . Перевод с французского Рубена Томаса. Кембридж: Cambridge University Press . ISBN 978-0-521-84425-3. Збл  1188.68177.
• Сипсер, Майкл (1997). Введение в теорию вычислений . Бостон: PWS. ISBN 0-534-94728-X.. Раздел 1.1: Конечные автоматы, стр. 31–47. Подраздел «Разрешимые проблемы, касающиеся регулярных языков» раздела 4.1: Разрешимые языки, стр. 152–155.4.4 DFA может принимать только регулярные языки