Моноид

В абстрактной алгебре , разделе математики , моноид — это множество, снабженное ассоциативной бинарной операцией и единичным элементом . Например, неотрицательные целые числа после сложения образуют моноид, единичный элемент которого равен $0$ .

Моноиды — это полугруппы с единицей. Такие алгебраические структуры встречаются в нескольких разделах математики.

Функции из множества в себя образуют моноид относительно композиции функций. В более общем смысле, в теории категорий морфизмы объекта самому себе образуют моноид, и, наоборот, моноид можно рассматривать как категорию с одним объектом.

В информатике и компьютерном программировании набор строк , построенный из заданного набора символов , представляет собой свободный моноид . Моноиды переходов и синтаксические моноиды используются при описании конечных автоматов . Моноиды трассировки и моноиды истории обеспечивают основу для вычислений процессов и параллельных вычислений .

В теоретической информатике изучение моноидов является фундаментальным для теории автоматов ( теория Крона–Родса ) и теории формального языка ( проблема высоты звезды ).

См. полугруппу , чтобы узнать об истории предмета и некоторых других общих свойствах моноидов.

Определение

Множество $S,$ снабженное бинарной операцией $S$ $\times$ $S$ $\to$ $S$ , которую мы обозначим $•$ , является моноидом, если оно удовлетворяет следующим двум аксиомам:

Ассоциативность: Для всех $a$ , $b$ и $c$ в $S$ справедливо уравнение $(a • b) • c = a • (b • c)$ .
Элемент идентификации: Существует элемент $e$ в $S$ такой, что для каждого элемента $a$ в $S$ выполняются равенства $e • a = a$ и $a • e = a$ .

Другими словами, моноид — это полугруппа с единицей . Ее также можно рассматривать как магму , обладающую ассоциативностью и идентичностью. Единичный элемент моноида уникален. ^[a] По этой причине тождество рассматривается как константа , т.е. $0$ -арная (или нулевая) операция. Таким образом, моноид характеризуется спецификацией тройки ( $S, •, e)$ .

В зависимости от контекста символ бинарной операции может быть опущен, так что операция обозначается сопоставлением ; например, аксиомы моноида могут быть записаны $(ab) c = a (bc)$ и $ea = ae = a$ . Это обозначение не означает, что речь идет об умножении чисел.

Моноид, в котором каждый элемент имеет обратный, является группой .

Моноидные структуры

Субмоноиды

Субмоноид моноида $($ $M$ $, •)$ — это подмножество $N$ из $M$ , замкнутое относительно операции моноида и содержащее единичный $элемент$ e из $M$ . ^[1]^[b] Символически $N$ является субмоноидом $M$ , если $e$ $\in$ $N$ $\subseteq$ $M$ , и $x$ $•$ $y$ $\in$ $N$ всякий раз, когда $x$ $,$ $y$ $\in$ $N$ . В этом случае $N$ является моноидом относительно бинарной операции, унаследованной от $M$ .

С другой стороны, если $N$ является подмножеством моноида, замкнутого относительно операции моноида, и является моноидом для этой унаследованной операции, то $N$ не всегда является субмоноидом, поскольку единичные элементы могут различаться. Например, одноэлементное множество ${0}$ замкнуто при умножении и не является подмоноидом (мультипликативного) моноида неотрицательных целых чисел .

Генераторы

Говорят, что подмножество $S$ множества $M$ порождает $M$ , если наименьший подмоноид $M$ , содержащий $S$ , есть $M$ . Если существует конечное множество, порождающее $M$ , то $M$ называется конечно порожденным моноидом .

Коммутативный моноид

Моноид, операция которого коммутативна , называется коммутативным моноидом (или, реже, абелевым моноидом ). Коммутативные моноиды часто записываются аддитивно. Любой коммутативный моноид наделен своим алгебраическим предварительным порядком $\leq$ , определяемым $x \leq y$ , если существует $z$ такой, что $x + z = y$ . ^[2] Порядковая единица коммутативного моноида $M$ — это элемент $u$ из $M$ такой, что для любого элемента $x$ из $M$ существует $v$ в множестве, порожденном $u$ , такой, что $x \leq v$ . Это часто используется в случае, если M $—$ положительный конус частично упорядоченной абелевой группы $G$ , и в этом случае мы говорим, что $u$ — единица порядка $G.$

Частично коммутативный моноид

Моноид, для которого операция коммутативна для некоторых, но не для всех элементов, является моноидом следа ; Моноиды трасс обычно встречаются в теории параллельных вычислений .

Примеры

Из 16 возможных бинарных логических операторов четыре имеют двустороннюю идентичность, которая также является коммутативной и ассоциативной. Каждый из этих четырех делает набор ${False, True}$ коммутативным моноидом. Согласно стандартным определениям, AND и XNOR имеют идентификатор $True$ , а XOR и OR имеют идентификатор $False$ . Моноиды от AND и OR также идемпотентны , а моноиды от XOR и XNOR — нет.
Множество натуральных чисел $N = {0, 1, 2, ...}$ является коммутативным моноидом при сложении (единичный элемент ) или умножении (единичный элемент 1 ). Субмоноид числа $N$ при сложении называется числовым моноидом .
Множество натуральных чисел $N ∖ {0}$ является коммутативным моноидом относительно умножения (единичный элемент $1$ ).
Учитывая набор $A$ , набор подмножеств $A$ является коммутативным моноидом при пересечении (единичный элемент - это сам $A$ ).
Учитывая набор $A$ , набор подмножеств $A$ является коммутативным моноидом при объединении (единичный элемент - это пустое множество ).
Обобщая предыдущий пример, каждая ограниченная полурешетка является идемпотентным коммутативным моноидом.
- В частности, любая ограниченная решетка может иметь как структуру моноида , так и структуру соединения . Элементами идентичности являются верх и низ решетки соответственно. Будучи решетками, гейтинговы алгебры и булевы алгебры наделены этими моноидными структурами.
Каждое одноэлементное множество ${x}$ , замкнутое относительно бинарной операции, $•$ образует тривиальный (одноэлементный) моноид, который также является тривиальной группой .
Каждая группа является моноидом, а каждая абелева группа — коммутативным моноидом.
Любую полугруппу S можно превратить в моноид, просто присоединив элемент e, не входящий в S , и определив e • s = s = s • e для всех s ∈ S . Это преобразование любой полугруппы в моноид осуществляется свободным функтором между категорией полугрупп и категорией моноидов. ^[3]
- Таким образом, идемпотентный моноид (иногда называемый find -first ) может быть сформирован путем присоединения единичного элемента e к левой нулевой полугруппе над множеством S. Противоположный моноид (иногда называемый find -last ) формируется из полугруппы правых нулей над S.
  - Присоедините тождество $e$ к полугруппе левых нулей с двумя элементами ${lt, gt}$ . Затем полученный идемпотентный моноид ${lt, e, gt}$ моделирует лексикографический порядок последовательности с учетом порядков ее элементов, где e представляет равенство.
Базовый набор любого кольца с операцией сложения или умножения. (По определению кольцо имеет мультипликативное тождество 1. )
- Целые числа , рациональные числа , действительные числа или комплексные числа со сложением или умножением в качестве операции. ^[4]
- Набор всех матриц размером $n$ на $n$ в заданном кольце со сложением или умножением матриц в качестве операции.
Множество всех конечных строк в некотором фиксированном алфавите $Σ$ образует моноид с операцией конкатенации строк . Пустая строка служит элементом идентификации. Этот моноид обозначается $Σ *$ и называется свободным моноидом над $Σ$ . Оно не коммутативно, если $Σ$ имеет хотя бы два элемента.
Для любого моноида $M$ противоположный моноид $M op$ имеет тот же набор несущих и единичный элемент, что и $M$ , и его работа определяется выражением $x • op y = y • x$ . Любой коммутативный моноид является противоположным себе моноидом.
Учитывая два множества $M$ и $N$ , наделенные структурой моноида (или, вообще говоря, любое конечное число моноидов, $M 1, ..., M k$ ), их декартово произведение $M \times N$ с бинарной операцией и единичным элементом, определенным на соответствующем координат, называемое прямым произведением , также является моноидом (соответственно $M 1 \times \cdot\cdot\cdot \times M k$ ). ^[5]
Зафиксируйте моноид $M$ . Множество всех функций из данного множества до $M$ также является моноидом. Элемент идентификации — это постоянная функция , сопоставляющая любое значение с идентификатором $M$ ; ассоциативная операция определяется поточечно .
Зафиксируйте моноид $M$ с операцией $•$ и единичным элементом $e$ $и$ рассмотрим его степенное множество $P (M)$ , состоящее из всех подмножеств M. Бинарная операция для таких подмножеств может быть определена как $S$ $•$ $T$ $= {$ $s$ $•$ $t$ $:$ $s$ $\in$ $S$ $,$ $t$ $\in$ $T$ $}$ . Это превращает $P$ $($ $M$ $)$ в моноид с единичным элементом ${$ $e$ $}$ . Точно так же степенное множество группы $G$ является моноидом относительно произведения групповых подмножеств .
Пусть $S$ — множество. Множество всех функций $S \to S$ образует моноид при композиции функций . Идентичность — это просто функция тождества . Его также называют $полным$ моноидом преобразования S . Если $S$ конечна с $n$ элементами, моноид функций на $S$ конечен с $n$ $n$ элементами.
Обобщая предыдущий пример, пусть $C$ — категория , а $X$ — объект $C.$ Множество всех эндоморфизмов X , обозначенное $End$ $C$ $($ $X$ $)$ $,$ образует моноид относительно композиции морфизмов . Дополнительную информацию о взаимосвязи между теорией категорий и моноидами см. ниже.
Множество классов гомеоморфизма компактных поверхностей со связной суммой . Ее единичным элементом является класс обычной 2-сферы. Более того, если $a$ обозначает класс тора , а $b$ обозначает класс проективной плоскости, то каждый элемент $c$ моноида имеет уникальное выражение вида $c$ $=$ $na$ $+$ $mb$ , где $n$ — целое положительное число и $m$ $= 0, 1$ или $2$ . У нас есть $3$ $b$ $=$ $a$ $+$ $b$ .
Пусть $⟨ f ⟩$ — циклический моноид порядка $n$ , то есть $⟨ f ⟩ = {f 0, f 1, ..., f n -1}$ . Тогда $f n = f k$ для некоторого $0 \leq k < n$ . Фактически, каждый такой $k$ дает отдельный моноид порядка $n$ , и каждый циклический моноид изоморфен одному из них.
Более того, $f$ можно рассматривать как функцию в точках ${0, 1, 2, ..., n -1}$ , заданную формулой

{\begin{bmatrix}0&1&2&\cdots &n-2&n-1\\1&2&3&\cdots &n-1&k\end{bmatrix}}

f(i):={\begin{cases}i+1,&{\text{if }}0\leq i<n-1\\k,&{\text{if }}i=n -1.\end{случаи}}

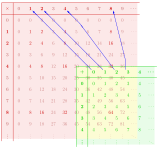
Умножение элементов в $⟨ f ⟩$ затем задаётся композицией функций.

Когда $k = 0$ , функция $f$ является перестановкой ${0, 1, 2, ..., n -1}$ и дает уникальную циклическую группу порядка $n$ .

Характеристики

Аксиомы моноида подразумевают, что единичный элемент $e$ уникален: если $e$ и $f$ являются единичными элементами моноида, то $e = ef = f$ .

Продукты и полномочия

Для каждого неотрицательного целого числа $n$ $можно$ рекурсивно определить произведение любой последовательности $($ $a$ $1$ $,$ $...,$ $a$ $n$ $)$ из $n$ элементов моноида: пусть $p$ $0$ $=$ $e$ и пусть $pm$ $=$ $pm$ $-1$ $•$ $a$ $m$ для $1 \leq$ $м$ $\leq$ $п$ . $p_{n}=\textstyle \prod _{i=1}^{n}a_{i}$

В качестве частного случая можно определить целые неотрицательные степени элемента $x$ моноида: $x 0 = 1$ и $x n = x n -1 • x$ для $n \geq 1$ . Тогда $x m + n = x m • x n$ для всех $m, n \geq 0$ .

Обратимые элементы

Элемент $x$ называется обратимым, если существует элемент $y$ такой, что $x • y = e$ и $y • x = e$ . Элемент $y$ называется обратным элементу $x$ . Инверсии, если они существуют, уникальны: если $y$ и $z$ являются инверсиями $x$ , то по ассоциативности $y = ey = (zx) y = z (xy) = ze = z$ . ^[6]

Если $x$ обратим, скажем, с обратным $y$ , то можно определить отрицательные степени $x$ , установив $x - n = y n$ для каждого $n \geq 1$ ; это делает уравнение $x m + n = x m • x n$ справедливым для всех $m, n \in Z.$

Совокупность всех обратимых элементов моноида вместе с операцией • образует группу .

Группа Гротендика

Не каждый моноид находится внутри группы. Например, вполне возможно иметь моноид, в котором существуют два элемента $a$ и $b$ , такие что $a • b = a$ выполняется, даже если $b$ не является единичным элементом. Такой моноид не может быть вложен в группу, потому что в группе, умножив обе части на обратную величину $a$ , получим $b = e$ , что неверно.

Моноид $(M, •)$ обладает свойством сокращения (или является сокращающимся), если для всех $a$ , $b$ и $c$ в $M$ равенство $a • b = a • c$ влечет $b = c$ , а равенство $b • a = c • а$ подразумевает $б = с$ .

Коммутативный моноид со свойством сокращения всегда можно вложить в группу с помощью групповой конструкции Гротендика . Именно так аддитивная группа целых чисел (группа с операцией $+$ ) строится из аддитивного моноида натуральных чисел (коммутативного моноида с операцией $+$ и свойством отмены). Однако некоммутативный сокращающийся моноид не обязательно должен быть вложимым в группу.

Если моноид обладает свойством сокращения и конечен , то он фактически является группой. ^[с]

Право- и левосократяющиеся элементы моноида поочередно образуют субмоноид (т. е. замкнуты относительно операции и, очевидно, содержат единицу). Это означает, что сокращающиеся элементы любого коммутативного моноида можно расширить до группы.

Свойство отмены в моноиде не обязательно для выполнения конструкции Гротендика – достаточно коммутативности. Однако если коммутативный моноид не обладает свойством сокращения, гомоморфизм моноида в его группу Гротендика не является инъективным. Точнее, если $a • b = a • c$ , то $b$ и $c$ имеют один и тот же образ в группе Гротендика, даже если $b \neq c$ . В частности, если моноид имеет поглощающий элемент , то его группа Гротендика является тривиальной группой .

Виды моноидов

Обратный моноид — это моноид, в котором для каждого $a$ в $M$ существует единственный $a -1$ в $M$ такой, что $a = a • a -1 • a$ и $a -1 = a -1 • a • a -1$ . Если инверсный моноид сократим, то он является группой.

В противоположном направлении, моноид без нулевой суммы — это аддитивно записанный моноид, в котором $a + b = 0$ означает, что $a = 0$ и $b = 0$ : ^[7] эквивалентно, что ни один элемент, кроме нуля, не имеет аддитивного обратного.

Действия и моноиды операторов

Пусть $M$ — моноид с бинарной операцией, обозначенной $•$ , и единичным элементом, обозначенным $e$ . Тогда (левый) $M$ -действие (или левый действие над $M$ ) представляет собой множество $X$ вместе с операцией $\cdot : M \times X \to X$ , которая совместима со структурой моноида следующим образом:

для всех $x$ в $X$ : $е \cdot x знак равно x$ ;
для всех $a$ , $b$ в $M$ и $x$ в $X$ : $а \cdot (б \cdot Икс) знак равно (а • б) \cdot Икс$ .

Это аналог действия (левой) группы в теории моноида . Правые $М$ -акты определяются аналогично. Моноид с действием также известен как моноид оператора . Важными примерами являются переходные системы полуавтоматов . Полугруппу преобразований можно превратить в моноид оператора путем присоединения тождественного преобразования.

Моноидные гомоморфизмы

Гомоморфизм между двумя моноидами $($ $M$ $, *)$ и $($ $N$ $, •)$ — это функция $f$ $:$ $M$ $\to$ $N$ такая, что

$ж (Икс * y) знак равно ж (Икс) • ж (y)$ для всех $x$ , $y$ в $M$
$ж (е M) знак равно е N$ ,

где $e M$ и $e N$ — тождества на $M$ и $N$ соответственно. Моноидные гомоморфизмы иногда называют просто моноидными морфизмами .

Не каждый гомоморфизм полугруппы между моноидами является гомоморфизмом моноида, поскольку он не может отображать тождество в тождество целевого моноида, даже если тождество является тождеством образа гомоморфизма. ^[d] Например, рассмотрим $[Z] n$ , набор классов вычетов по модулю $n$ , оснащенный функцией умножения. В частности, $[1] n$ является единичным элементом. Функция $f : [Z] 3 \to [Z] 6$ , заданная формулой $[k] 3 \mapsto [3 k] 6$ , является гомоморфизмом полугруппы, поскольку $[3 k \cdot 3 l] 6 = [9 kl] 6 = [3 kl] 6$ . Однако $f ([1] 3) = [3] 6 \neq [1] 6$ , поэтому гомоморфизм моноида — это гомоморфизм полугруппы между моноидами, который отображает идентичность первого моноида в идентичность второго моноида, и последнее условие не может быть опущено.

Напротив, гомоморфизм полугрупп между группами всегда является гомоморфизмом группы , поскольку он обязательно сохраняет идентичность (потому что в целевой группе гомоморфизма единичный элемент является единственным элементом $x$ таким, что $x \cdot x = x$ ).

Биективный моноидный гомоморфизм называется моноидным изоморфизмом . Два моноида называются изоморфными, если между ними существует моноидный изоморфизм.

Уравненное представление

Моноидам может быть предоставлено представление , во многом таким же образом, как группы могут быть определены посредством группового представления . Это делается путем задания набора образующих $Σ$ и набора отношений на свободном моноиде $Σ *$ . Это делается путем расширения (конечных) бинарных отношений на $Σ *$ до конгруэнций моноидов, а затем построения фактормоноида, как указано выше.

Для бинарного отношения $R \subset Σ * \times Σ *$ его симметричное замыкание определяется как $R \cup R -1$ . Это можно расширить до симметричного отношения $E \subset Σ * \times Σ *$ , определив $x ~ E y$ тогда и только тогда, когда $x = sut$ и $y = svt$ для некоторых строк $u, v, s, t \in Σ *$ с $(u, v) \in р \cup р -1$ . Наконец, берется рефлексивное и транзитивное замыкание $E$ , которое тогда является моноидным сравнением.

$В$ типичной ситуации отношение $R$ просто задается как набор уравнений, так что $R = {u 1 = v 1, ..., un = v n}$ . Так, например,

\langle p,q\,\vert \;pq=1\rangle

— эквациональное представление бициклического моноида , и

\langle a,b\,\vert \;aba=baa,bba=bab\rangle

— пластический моноид степени $2$ (имеет бесконечный порядок). Элементы этого пластического моноида можно записать как целые числа $i$ , $j$ , $k$ , поскольку соотношения показывают, что $ba$ коммутирует как с $a$ , так и $с b$ . $a^{i}b^{j}(ba)^{k}$

Связь с теорией категорий

Моноиды можно рассматривать как особый класс категорий . Действительно, аксиомы, необходимые для моноидной операции, в точности совпадают с аксиомами, необходимыми для композиции морфизмов , если они ограничены набором всех морфизмов, источником и целью которых является данный объект. ^[8] То есть

Моноид — это, по сути, то же самое, что и категория с единственным объектом.

Точнее, учитывая моноид $(M, •)$ , можно построить небольшую категорию только с одним объектом, морфизмы которой являются элементами $M.$ Композиция морфизмов задается моноидной операцией $•$ .

Аналогично, моноидные гомоморфизмы — это просто функторы между отдельными категориями объектов. ^[8] Таким образом, эта конструкция дает эквивалентность между категорией (малых) моноидов Mon и полной подкатегорией категории (малых) категорий Cat . Аналогично категория групп эквивалентна другой полной подкатегории Cat .

В этом смысле теорию категорий можно рассматривать как расширение концепции моноида. Многие определения и теоремы о моноидах можно обобщить на небольшие категории с более чем одним объектом. Например, фактор категории с одним объектом — это просто фактормоноид.

Моноиды, как и другие алгебраические структуры, также образуют свою собственную категорию Mon , объекты которой являются моноидами, а морфизмы — гомоморфизмами моноидов. ^[8]

Существует также понятие моноидного объекта , которое представляет собой абстрактное определение того, что такое моноид в категории. Моноидный объект в Set — это просто моноид.

Моноиды в информатике

В информатике многие абстрактные типы данных могут быть наделены моноидной структурой. В обычном шаблоне последовательность элементов моноида « складывается » или «накапливается» для получения окончательного значения. Например, многим итеративным алгоритмам необходимо обновлять некий «промежуточный итог» на каждой итерации; этот шаблон может быть элегантно выражен с помощью моноидной операции. Альтернативно, ассоциативность моноидных операций гарантирует, что операцию можно распараллелить , используя сумму префиксов или аналогичный алгоритм, чтобы эффективно использовать несколько ядер или процессоров.

Учитывая последовательность значений типа $M$ с единичным элементом $ε$ и ассоциативной операцией $•$ , операция складки определяется следующим образом:

\mathrm {fold} :M^{*}\rightarrow M=\ell \mapsto {\begin{cases}\varepsilon &{\mbox{if }}\ell =\mathrm {nil} \\m\bullet \mathrm {fold} \,\ell '&{\mbox{if }}\ell =\mathrm {cons} \,m\,\ell '\end{cases}}

Кроме того, любую структуру данных можно «свернуть» аналогичным образом, учитывая сериализацию ее элементов. Например, результат «свертывания» двоичного дерева может отличаться в зависимости от обхода дерева до и после порядка .

Уменьшение карты

Применением моноидов в информатике является так называемая модель программирования MapReduce (см. Кодирование Map-Reduce как моноида со сворачиванием влево). MapReduce в вычислительной технике состоит из двух или трех операций. Учитывая набор данных, «Карта» состоит из сопоставления произвольных данных с элементами определенного моноида. «Уменьшение» заключается в складывании этих элементов так, чтобы в итоге мы получили только один элемент.

Например, если у нас есть мультимножество , в программе оно представляется в виде отображения элементов на их номера. В этом случае элементы называются ключами. Количество различных ключей может быть слишком большим, и в этом случае мультимножество шардируется . Чтобы правильно завершить сокращение, на этапе «Перетасовка» данные перегруппируются по узлам. Если нам не нужен этот шаг, вся операция Map/Reduce состоит из сопоставления и сокращения; обе операции распараллеливаемы: первая из-за ее поэлементной природы, вторая - из-за ассоциативности моноида.

Полные моноиды

Полный моноид — это коммутативный моноид, снабженный операцией бесконечной суммы для любого набора индексов $I$ такого, что ^[9]^[10]^[11]^[12] $\Sigma _{I}$

\sum _{i\in \emptyset }{m_{i}}=0;\quad \sum _{i\in \{j\}}{m_{i}}=m_{j};\quad \sum _{i\in \{j,k\}}{m_{i}}=m_{j}+m_{k}\quad {\text{ for }}j\neq k

\sum _{j\in J}{\sum _{i\in I_{j}}{m_{i}}}=\sum _{i\in I}m_{i}\quad {\text{ if }}\bigcup _{j\in J}I_{j}=I{\text{ and }}I_{j}\cap I_{j'}=\emptyset \quad {\text{ for }}j\neq j'

Упорядоченный коммутативный моноид — это коммутативный моноид $M$ вместе с частичным упорядочением $\leq$ такой, что $a \geq 0$ для каждого $a \in M$ , а $a \leq b$ влечет за собой $a + c \leq b + c$ для всех $a, b, c \in M.$

Непрерывный моноид — это упорядоченный коммутативный моноид $(M, \leq)$ , в котором каждое направленное подмножество имеет наименьшую верхнюю границу , и эти наименьшие верхние границы совместимы с операцией моноида:

a+\sup S=\sup(a+S)

для каждого $a \in M$ и направленного подмножества $S$ из $M$ .

Если $(M, \leq)$ — непрерывный моноид, то для любого набора индексов $I$ и набора элементов $(a i) i \in I$ можно определить

\sum _{I}a_{i}=\sup _{{\text{finite }}E\subset I}\;\sum _{E}a_{i},

и $M$ вместе с этой операцией бесконечной суммы представляет собой полный моноид. ^[12]

Смотрите также

Примечания

^ Если и e1 $, и$ e2 $удовлетворяют приведенным$ $выше$ уравнениям $,$ $то$ $e1 = e1 • e2 = e2 .$
^ Некоторые авторы опускают требование о том, что субмоноид должен содержать единичный элемент из своего определения, требуя только того, чтобы он имел единичный элемент, который может отличаться от элемента $M$ .
^ Доказательство: зафиксируйте элемент $x$ в моноиде. Поскольку моноид конечен, $x n = x m$ для некоторого $m > n > 0$ . Но тогда, сокращая, мы получаем $x m - n = e$ , где $e$ — единица. Следовательно, $x • x m - n -1 = e$ , поэтому $x$ имеет обратный.
^ $f (x) * f (e M) знак равно f (x * e M) знак равно f (x)$ для каждого $x$ в $M$ , когда $f$ - гомоморфизм полугруппы, а $e M$ - тождество ее моноида области $M$ .

Цитаты

^ Джейкобсон 2009
^ Гондран и Мину 2008, с. 13
^ Родос и Стейнберг 2009, с. 22
^ Джейкобсон 2009, с. 29, примеры 1, 2, 4 и 5
^ Джейкобсон 2009, с. 35
^ Джейкобсон 2009, с. 31, §1.2
^ Верунг 1996 г.
^ abc Awodey 2006, с. 10
^ Дросте и Куич 2009, стр. 7–10.
^ Хебиш 1992
^ Куич 1990
^ аб Куич 2011.

Внешние ссылки

«Моноид», Математическая энциклопедия , EMS Press , 2001 [1994]
Вайсштейн, Эрик В. «Моноид». Математический мир .
Моноид в PlanetMath .