Деформация (инженерная)

В инженерии деформация (изменение размера или формы объекта) может быть упругой или пластичной . Если деформация незначительна , объект называется жестким .

Основные понятия

Возникновение деформации в инженерных приложениях основано на следующих основных концепциях:

Смещения — это любые изменения положения точки на объекте, включая перемещения и вращения всего тела ( жёсткие преобразования ).
Деформация — это изменение относительного положения внутренних точек объекта, за исключением жестких преобразований, приводящее к изменению формы или размера тела.
Деформация — это относительная внутренняя деформация, безразмерное изменение формы бесконечно малого куба материала относительно исходной конфигурации. Механические деформации вызываются механическим напряжением , см. кривую зависимости деформации от напряжения .

Соотношение между напряжением и деформацией обычно линейное и обратимое вплоть до предела текучести , а деформация является упругой . Упругость в материалах возникает, когда приложенное напряжение не превышает энергии, необходимой для разрыва молекулярных связей, что позволяет материалу обратимо деформироваться и возвращаться к своей первоначальной форме после снятия напряжения. Линейное соотношение для материала известно как модуль Юнга . Выше предела текучести некоторая степень постоянной деформации остается после разгрузки и называется пластической деформацией . Определение напряжения и деформации во всем твердом объекте дается полем прочности материалов , а для конструкции — структурным анализом .

На рисунке выше можно увидеть, что сжимающая нагрузка (указана стрелкой) вызвала деформацию в цилиндре , так что первоначальная форма (пунктирные линии) изменилась (деформировалась) в форму с выпуклыми сторонами. Стороны выпирают, потому что материал, хотя и достаточно прочен, чтобы не трескаться или иным образом не разрушаться, недостаточно прочен, чтобы выдерживать нагрузку без изменений. В результате материал выдавливается вбок. Внутренние силы (в данном случае под прямым углом к деформации) сопротивляются приложенной нагрузке.

Виды деформации

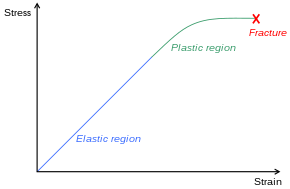
В зависимости от типа материала, размера и геометрии объекта, а также приложенных сил могут возникнуть различные типы деформации. На изображении справа показана инженерная диаграмма напряжения и деформации для типичного пластичного материала, такого как сталь. Различные режимы деформации могут возникать при различных условиях, что можно изобразить с помощью карты механизма деформации .

Постоянная деформация необратима; деформация сохраняется даже после снятия приложенных сил, тогда как временная деформация восстанавливается, так как исчезает после снятия приложенных сил. Временная деформация также называется упругой деформацией, тогда как постоянная деформация называется пластической деформацией.

Упругая деформация

Изучение временной или упругой деформации в случае инженерной деформации применяется к материалам, используемым в машиностроении и строительстве, таким как бетон и сталь , которые подвергаются очень малым деформациям. Инженерная деформация моделируется теорией бесконечно малых деформаций , также называемой теорией малых деформаций , теорией малых деформаций , теорией малых смещений или теорией малых градиентов смещений , где деформации и вращения являются как малыми.

Для некоторых материалов, например эластомеров и полимеров, подвергающихся большим деформациям, инженерное определение деформации неприменимо, например типичные инженерные деформации больше 1%, ^[1] , поэтому требуются другие более сложные определения деформации, такие как растяжение , логарифмическая деформация , деформация Грина и деформация Альманси . Эластомеры и металлы с памятью формы , такие как нитинол, демонстрируют большие диапазоны упругой деформации, как и резина . Однако эластичность в этих материалах нелинейна.

Обычные металлы, керамика и большинство кристаллов демонстрируют линейную упругость и меньший диапазон упругости.

Линейная упругая деформация подчиняется закону Гука , который гласит:

\sigma =E\varepsilon

где

$σ$ — приложенное напряжение ;
$E$ — константа материала, называемая модулем Юнга или модулем упругости ;
$ε$ — результирующая деформация .

Это соотношение применимо только в упругом диапазоне и указывает на то, что наклон кривой напряжения и деформации может быть использован для нахождения модуля Юнга ( $E$ ). Инженеры часто используют этот расчет в испытаниях на растяжение. Площадь под этой упругой областью известна как упругость.

Обратите внимание, что не все упругие материалы подвергаются линейной упругой деформации; некоторые, такие как бетон , серый чугун и многие полимеры, реагируют нелинейно. Для этих материалов закон Гука неприменим. ^[2]

Разница в истинных и инженерных кривых напряжения-деформации

Пластическая деформация

Этот тип деформации не отменяется просто снятием приложенной силы. Однако объект в диапазоне пластической деформации сначала подвергнется упругой деформации, которая отменяется просто снятием приложенной силы, поэтому объект частично вернется к своей первоначальной форме. Мягкие термопластики имеют довольно большой диапазон пластической деформации, как и пластичные металлы, такие как медь , серебро и золото . Сталь тоже имеет, но не чугун . Твердые термореактивные пластики, резина, кристаллы и керамика имеют минимальный диапазон пластической деформации. Примером материала с большим диапазоном пластической деформации является влажная жевательная резинка , которую можно растянуть в десятки раз по сравнению с ее первоначальной длиной.

Под действием растягивающего напряжения пластическая деформация характеризуется областью деформационного упрочнения и областью образования шейки и, наконец, разрушением (также называемым разрывом). Во время деформационного упрочнения материал становится прочнее за счет движения атомных дислокаций . Фаза образования шейки обозначается уменьшением площади поперечного сечения образца. Образование шейки начинается после достижения предельной прочности. Во время образования шейки материал больше не может выдерживать максимальное напряжение, и деформация в образце быстро увеличивается. Пластическая деформация заканчивается разрушением материала.

Диаграмма кривой зависимости деформации от напряжения , показывающая соотношение между напряжением (приложенной силой) и деформацией (деформацией) пластичного металла.

Отказ

Разрушение при сжатии

Обычно сжимающее напряжение, приложенное к стержням, колоннам и т. д., приводит к их укорочению.

Нагрузка на структурный элемент или образец увеличит сжимающее напряжение до тех пор, пока оно не достигнет предела прочности на сжатие . В зависимости от свойств материала режимы разрушения являются текучестью для материалов с пластичным поведением (большинство металлов , некоторые почвы и пластики ) или разрывом для материалов с хрупким поведением (геоматериалы, чугун , стекло и т. д.).

В длинных, тонких элементах конструкции, таких как колонны или фермы , увеличение сжимающей силы F приводит к разрушению конструкции из-за потери устойчивости при более низком напряжении, чем предел прочности при сжатии.

Перелом

Разрыв происходит после того, как материал достигает конца упругого, а затем пластического диапазона деформации. В этот момент силы накапливаются до тех пор, пока не станут достаточными для того, чтобы вызвать разрыв. Все материалы в конечном итоге разрушаются, если приложены достаточные силы.

Виды стресса и напряжения

Инженерное напряжение и инженерная деформация являются приближениями к внутреннему состоянию, которое может быть определено из внешних сил и деформаций объекта, при условии, что нет значительного изменения размера. Когда есть значительное изменение размера, истинное напряжение и истинная деформация могут быть выведены из мгновенного размера объекта.

Инженерные напряжения и деформации

Рассмотрим стержень с исходной площадью поперечного сечения $A 0,$ подвергаемый воздействию равных и противоположных сил $F,$ тянущих на концах, так что стержень находится под напряжением. Материал испытывает напряжение, определяемое как отношение силы к площади поперечного сечения стержня, а также осевое удлинение:

Нижний индекс 0 обозначает исходные размеры образца. Производная единица измерения напряжения в системе СИ — ньютоны на квадратный метр или паскали (1 паскаль = 1 Па = 1 Н/м ² ), а деформация — безразмерная величина . Кривая зависимости напряжения от деформации для этого материала строится путем удлинения образца и регистрации изменения напряжения с деформацией до тех пор, пока образец не сломается . По соглашению деформация откладывается по горизонтальной оси, а напряжение — по вертикальной. Обратите внимание, что в инженерных целях мы часто предполагаем, что площадь поперечного сечения материала не изменяется в течение всего процесса деформации. Это неверно, поскольку фактическая площадь будет уменьшаться при деформации из-за упругой и пластической деформации. Кривая, основанная на исходном поперечном сечении и длине датчика, называется инженерной кривой зависимости напряжения от деформации , в то время как кривая, основанная на мгновенной площади поперечного сечения и длине, называется истинной кривой зависимости напряжения от деформации . Если не указано иное, обычно используется инженерная зависимость напряжения от деформации .

Настоящий стресс и напряжение

В приведенных выше определениях инженерных напряжений и деформаций игнорируются два поведения материалов при испытаниях на растяжение:

уменьшение площади сечения
усложнение развития удлинения

Истинное напряжение и истинная деформация определяются иначе, чем инженерное напряжение и деформация, чтобы учесть эти поведения. Они задаются как

Здесь размеры являются мгновенными значениями. Предполагая, что объем образца сохраняется и деформация происходит равномерно,

A_{0}L_{0}=AL

Истинное напряжение и деформация могут быть выражены инженерным напряжением и деформацией. Для истинного напряжения,

\sigma _{\mathrm {t} }={\frac {F}{A}}={\frac {F}{A_{0}}}{\frac {A_{0}}{A}}={\frac {F}{A_{0}}}{\frac {L}{L_{0}}}=\sigma (1+\varepsilon )

Для штамма,

\delta \varepsilon _{\mathrm {t} }={\frac {\delta L}{L}}

Интегрируем обе стороны и применяем граничное условие,

\varepsilon _{\mathrm {t} }=\ln \left({\frac {L}{L_{0}}}\right)=\ln(1+\varepsilon )

Таким образом, при испытании на растяжение истинное напряжение больше инженерного напряжения, а истинная деформация меньше инженерной деформации. Таким образом, точка, определяющая истинную кривую напряжение-деформация, смещается вверх и влево, чтобы определить эквивалентную инженерную кривую напряжение-деформация. Разница между истинными и инженерными напряжениями и деформациями будет увеличиваться с пластической деформацией. При низких деформациях (таких как упругая деформация) разница между ними незначительна. Что касается точки предела прочности на растяжение, то это максимальная точка на инженерной кривой напряжение-деформация, но не особая точка на истинной кривой напряжение-деформация. Поскольку инженерное напряжение пропорционально силе, приложенной вдоль образца, критерий образования шейки можно установить как $\delta F=0.$

{\begin{aligned}&\delta F=\sigma _{\text{t}}\,\delta A+A\,\delta \sigma _{\text{t}}=0\\&-{\frac {\delta A}{A}}={\frac {\delta \sigma _{\mathrm {t} }}{\sigma _{\mathrm {t} }}}\end{aligned}}

Этот анализ предполагает природу точки предельной прочности на растяжение (UTS). Эффект упрочнения работой точно уравновешивается сокращением площади сечения в точке UTS.

После образования шейки образец подвергается неоднородной деформации, поэтому приведенные выше уравнения недействительны. Напряжение и деформация в шейке могут быть выражены как:

{\begin{aligned}\sigma _{\mathrm {t} }&={\frac {F}{A_{\mathrm {neck} }}}\\\varepsilon _{\mathrm {t} }&=\ln \left({\frac {A_{0}}{A_{\mathrm {neck} }}}\right)\end{aligned}}

Для описания взаимосвязи между истинным напряжением и истинной деформацией обычно используется эмпирическое уравнение .

\sigma _{\mathrm {t} }=K(\varepsilon _{\mathrm {t} })^{n}

Здесь $n$ — показатель степени деформационного упрочнения, а $K$ — коэффициент прочности. $n$ — мера поведения материала при деформационном упрочнении. Материалы с более высоким $n$ имеют большую устойчивость к образованию шейки. Обычно металлы при комнатной температуре имеют $n$ в диапазоне от 0,02 до 0,5. ^[3]

Обсуждение

Поскольку мы не учитываем изменение площади во время деформации выше, истинная кривая напряжения и деформации должна быть выведена заново. Для вывода кривой напряжения-деформации мы можем предположить, что изменение объема равно 0, даже если мы деформировали материалы. Мы можем предположить, что:

A_{i}\times \varepsilon _{i}=A_{f}\times \varepsilon _{f}

Тогда истинное напряжение можно выразить следующим образом:

{\begin{aligned}\sigma _{T}={\frac {F}{A_{f}}}&={\frac {F}{A_{i}}}\times {\frac {A_{i}}{A_{f}}}\\&=\sigma _{e}\times {\frac {l_{f}}{l_{i}}}\\[2pt]&=\sigma _{E}\times {\frac {l_{i}+\delta l}{l_{i}}}\\[2pt]&=\sigma _{E}(1+\varepsilon _{E})\end{aligned}}

Кроме того, истинную деформацию $ε T$ можно выразить следующим образом:

\varepsilon _{T}={\frac {dl}{l_{0}}}+{\frac {dl}{l_{1}}}+{\frac {dl}{l_{2}}}+\cdots =\sum _{i}{\frac {dl}{l_{i}}}

Тогда мы можем выразить значение как

\int _{l_{0}}^{l_{i}}{\frac {dl}{l}}\,dx=\ln \left({\frac {l_{i}}{l_{0}}}\right)=\ln(1+\varepsilon _{E})

Таким образом, мы можем построить сюжет в терминах и как правильную фигуру. $\sigma _{T}$ $\varepsilon _{E}$

Кроме того, на основе истинной кривой напряжения-деформации мы можем оценить область, где начинается образование шейки. Поскольку образование шейки начинает появляться после предельного растягивающего напряжения, где прикладывается максимальная сила, мы можем выразить эту ситуацию следующим образом:

dF=0=\sigma _{T}dA_{i}+A_{i}d\sigma _{T}

поэтому эту форму можно выразить следующим образом:

{\frac {d\sigma _{T}}{\sigma _{T}}}=-{\frac {dA_{i}}{A_{i}}}

Это указывает на то, что шейка начинает появляться там, где уменьшение площади становится гораздо более значительным по сравнению с изменением напряжения. Затем напряжение будет локализовано в определенной области, где появляется шейка.

Кроме того, мы можем вывести различные зависимости на основе истинной кривой напряжения-деформации.

1) Кривая истинной деформации и напряжения может быть выражена приблизительной линейной зависимостью путем взятия логарифма истинного напряжения и деформации. Связь может быть выражена следующим образом:

\sigma _{T}=K\times (\varepsilon _{T})^{n}

Где — коэффициент напряжения, а — коэффициент деформационного упрочнения. Обычно значение находится в диапазоне от 0,02 до 0,5 при комнатной температуре. Если равно 1, то мы можем выразить этот материал как идеальный упругий материал. ^[4]^[5] $K$ $n$ $n$ $n$

2) В действительности, напряжение также сильно зависит от скорости изменения деформации. Таким образом, мы можем вывести эмпирическое уравнение, основанное на изменении скорости деформации.

\sigma _{T}=K'\times ({\dot {\varepsilon _{T}}})^{m}

Истинная кривая напряжения-деформации ГЦК металла и ее производная форма ^[4]

Где константа, связанная с напряжением течения материала. указывает производную деформации по времени, которая также известна как скорость деформации. является чувствительностью к скорости деформации. Кроме того, значение связано с сопротивлением образованию шейки. Обычно значение находится в диапазоне 0-0,1 при комнатной температуре и достигает 0,8 при повышении температуры. $K'$ ${\dot {\varepsilon _{T}}}$ $m$ $m$ $m$

Объединив 1) и 2), мы можем создать окончательное соотношение, как показано ниже:

\sigma _{T}=K''\times (\varepsilon _{T})^{n}({\dot {\varepsilon _{T}}})^{m}

Где — глобальная константа, связывающая деформацию, скорость деформации и напряжение. $K''$

3) На основе истинной кривой напряжения-деформации и ее производной формы мы можем оценить деформацию, необходимую для начала образования шейки. Ее можно рассчитать на основе пересечения истинной кривой напряжения-деформации, как показано справа.

На этом рисунке также показана зависимость деформации шейки от различных температур. В случае металлов FCC обе кривые напряжение-деформация в ее производной сильно зависят от температуры. Поэтому при более высокой температуре шейка начинает появляться даже при более низком значении деформации.

Все эти свойства указывают на важность расчета истинной кривой «напряжение-деформация» для дальнейшего анализа поведения материалов в условиях внезапных внешних воздействий.

4) Графический метод, так называемый "Considere construction", может помочь определить поведение кривой напряжения-деформации, происходит ли на образце сужение или вытяжка. При установке в качестве определителя истинное напряжение и деформация могут быть выражены с помощью инженерного напряжения и деформации, как показано ниже: $\lambda =L/L_{0}$

\sigma _{T}=\sigma _{e}\times \lambda ,\qquad \varepsilon _{T}=\ln \lambda .

Следовательно, значение инженерного напряжения можно выразить секущей линией, образованной истинным напряжением и значением , где к . Анализируя форму диаграммы и секущей линии, мы можем определить, проявляют ли материалы вытяжку или сужение. $\lambda$ $\lambda =0$ $\lambda =1$ $\sigma _{T}-\lambda$

Рассмотрим график. (a) Истинная кривая напряжения-деформации без касательных. Нет ни шейки, ни вытяжки. (b) С одной касательной. Есть только шейка. (c) С двумя касательными. Есть и шейка, и вытяжка. ^[6]

На рисунке (a) есть только вогнутый вверх график Considere. Это указывает на то, что нет падения текучести, поэтому материал будет подвержен разрушению до того, как он течет. На рисунке (b) есть определенная точка, где касательная совпадает с секущей линией в точке, где . После этого значения наклон становится меньше секущей линии, где начинает появляться шейка. На рисунке (c) есть точка, где начинает появляться текучесть, но когда , происходит вытяжка. После вытяжки весь материал растянется и в конечном итоге покажет трещину. Между и сам материал не растягивается, а скорее начинает растягиваться только шейка. $\lambda =\lambda _{Y}$ $\lambda =\lambda _{d}$ $\lambda _{Y}$ $\lambda _{d}$

Заблуждения

Популярное заблуждение заключается в том, что все материалы, которые гнутся, являются «слабыми», а те, которые не гнутся, являются «прочными». В действительности, многие материалы, которые подвергаются большим упругим и пластическим деформациям, такие как сталь, способны поглощать напряжения, которые могли бы привести к разрушению хрупких материалов, таких как стекло, с минимальным диапазоном пластической деформации. ^[7]

Смотрите также

Ссылки

^ Риз, Дэвид (2006). Основы инженерной пластичности: Введение в инженерные и производственные приложения. Баттерворт-Хайнеманн. стр. 41. ISBN 0-7506-8025-3. Архивировано из оригинала 2017-12-22.
^ Каллистер, Уильям Д. (2004) Основы материаловедения и инженерии , John Wiley and Sons, 2-е изд., стр. 184. ISBN 0-471-66081-7 .
^ Кортни, Томас (2005). Механическое поведение материалов . Waveland Press, Inc., стр. 6–13.
^ ab Courtney, Thomas (2000). Механическое поведение материалов . Иллинойс: Waveland Press. стр. 165. ISBN 9780073228242.
^ "True Stress and Strain" (PDF) . Архивировано из оригинала (PDF) 2018-01-27 . Получено 2018-05-15 .
^ Роланд, Дэвид. «КРИВЫЕ НАПРЯЖЕНИЕ-ДЕФОРМАЦИЯ» (PDF) . Массачусетский технологический институт .
^ Райс, Питер и Даттон, Хью (1995). Структурное стекло. Тейлор и Фрэнсис. стр. 33. ISBN 0-419-19940-3.{{cite book}}: CS1 maint: multiple names: authors list (link)