Диаграмма пространства-времени

График пространства и времени в специальной теории относительности

Мировая линия (желтый путь) фотона , которая находится в точке x = 0 в момент времени ct = 0.

Пространственно-временная диаграмма — это графическая иллюстрация местоположений в пространстве в разное время, особенно в специальной теории относительности . Пространственно-временные диаграммы могут показывать геометрию, лежащую в основе таких явлений, как замедление времени и сокращение длины, без математических уравнений.

История местоположения объекта во времени вычерчивает линию или кривую на пространственно-временной диаграмме, называемую мировой линией объекта . Каждая точка на пространственно-временной диаграмме представляет собой уникальное положение в пространстве и времени и называется событием .

Наиболее известный класс пространственно-временных диаграмм известен как диаграммы Минковского , разработанные Германом Минковским в 1908 году. Диаграммы Минковского представляют собой двумерные графики, которые изображают события, происходящие во вселенной, состоящей из одного пространственного измерения и одного временного измерения. В отличие от обычного графика расстояние-время, расстояние отображается на горизонтальной оси, а время на вертикальной оси. Кроме того, единицы измерения времени и пространства выбираются таким образом, что объект, движущийся со скоростью света, изображается следующим под углом 45° к осям диаграммы.

Введение в кинетические диаграммы

Графики зависимости положения от времени

Рис 1-1. График зависимости положения от времени.

При изучении одномерной кинематики графики положения и времени (сокращенно называемые графиками xt) являются полезным средством для описания движения. Кинематические характеристики, помимо положения объекта, видны по наклону и форме линий. ^[1] На рис. 1-1 изображенный объект движется от начала координат с положительной постоянной скоростью (1,66 м/с) в течение 6 секунд, останавливается на 5 секунд, затем возвращается в начало координат в течение 7 секунд с непостоянной скоростью (но отрицательной скоростью).

На самом базовом уровне диаграмма пространства-времени — это просто график времени и положения, в котором направления осей в обычном графике pt поменялись местами; то есть вертикальная ось относится к временным, а горизонтальная — к пространственным значениям координат. Особенно при использовании в специальной теории относительности (СТО) временные оси диаграммы пространства-времени часто масштабируются со скоростью света c и, таким образом, часто обозначаются как ct. Это изменяет размерность рассматриваемой физической величины с < Времени > на < Длину > в соответствии с размерностью, связанной с пространственной осью, которая часто обозначается как x.

Стандартная конфигурация систем отсчета

Рис 1-2. Диаграмма Галилея двух систем отсчета в стандартной конфигурации.

Чтобы облегчить понимание того, как координаты пространства-времени, измеренные наблюдателями в разных системах отсчета , сравниваются друг с другом, полезно стандартизировать и упростить установку. Две галилеевы системы отсчета (т. е. обычные трехмерные системы отсчета), S и S′ (произносится как «S prime»), каждая с наблюдателями O и O′, покоящимися в своих соответствующих системах, но измеряющими другую как движущуюся со скоростями ± v, называются находящимися в стандартной конфигурации , когда:

• Оси x , y , z кадра S ориентированы параллельно соответствующим штрихованным осям кадра S′.
• Начало координат кадров S и S′ совпадает в момент времени t = 0 в кадре S, а также в момент времени t ′ = 0 в кадре S′. ^{[2] : 107}
• Кадр S′ движется в направлении x кадра S со скоростью v , измеренной в кадре S.

Эта пространственная установка отображена на рис. 1-2, на котором временные координаты отдельно аннотируются как величины t и t' .

На следующем этапе упрощения часто бывает достаточно рассмотреть только направление наблюдаемого движения и проигнорировать два других пространственных компонента, что позволяет изобразить x и ct на двумерных пространственно-временных диаграммах, как было представлено выше.

Нерелятивистские «диаграммы пространства-времени»

Рис 1-3. В ньютоновской физике для обоих наблюдателей событие в точке А приписывается одному и тому же моменту времени.

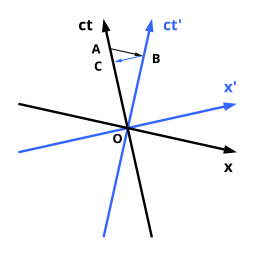
Черные оси, обозначенные x и ct на рис. 1-3, являются системой координат наблюдателя, называемого покоящимся , и который расположен в точке x = 0. Мировая линия этого наблюдателя идентична оси времени ct . Каждая параллельная этой оси линия также будет соответствовать объекту, находящемуся в состоянии покоя, но в другом положении. Синяя линия описывает объект, движущийся с постоянной скоростью v вправо, например, движущийся наблюдатель.

Эту синюю линию, обозначенную ct ′, можно интерпретировать как ось времени для второго наблюдателя. Вместе с осью x , которая идентична для обоих наблюдателей, она представляет их систему координат. Поскольку системы отсчета находятся в стандартной конфигурации, оба наблюдателя согласны относительно местоположения начала своих систем координат. Оси для движущегося наблюдателя не перпендикулярны друг другу, а шкала на их оси времени растянута. Чтобы определить координаты определенного события, необходимо построить две линии, каждая из которых параллельна одной из двух осей, проходящие через событие, и считать их пересечения с осями.

Определение положения и времени события A в качестве примера на диаграмме приводит к одному и тому же времени для обоих наблюдателей, как и ожидалось. Только для положения получаются разные значения, поскольку движущийся наблюдатель приблизился к положению события A с момента t = 0. В общем случае все события на линии, параллельной оси x , происходят одновременно для обоих наблюдателей. Существует только одно универсальное время t = t ′ , моделирующее существование одной общей оси положения. С другой стороны, из-за двух разных осей времени наблюдатели обычно измеряют разные координаты для одного и того же события. Этот графический перевод из x и t в x ′ и t ′ и наоборот математически описывается так называемым преобразованием Галилея .

Диаграммы Минковского

Обзор

Рис. 2-1 В теории относительности каждый наблюдатель относит событие в точке А к разному времени и месту.

Рис 2-2 Диаграмма Минковского для различных скоростей штрихованной рамки, движущейся относительно нештрихованной рамки. Пунктирные линии представляют световой конус вспышки света в начале координат.

Термин «диаграмма Минковского» относится к особой форме диаграммы пространства-времени, часто используемой в специальной теории относительности. Диаграмма Минковского — это двумерное графическое изображение части пространства Минковского , обычно там, где пространство свернуто до одного измерения. Единицы измерения в этих диаграммах берутся таким образом, что световой конус в событии состоит из линий наклона плюс или минус один, проходящих через это событие. ^[3] Горизонтальные линии соответствуют обычному понятию одновременных событий для неподвижного наблюдателя в начале координат.

Конкретная диаграмма Минковского иллюстрирует результат преобразования Лоренца . Преобразование Лоренца связывает две инерциальные системы отсчета , где наблюдатель, неподвижный в точке события (0, 0), изменяет скорость вдоль оси x . Как показано на рис. 2-1, новая ось времени наблюдателя образует угол α с предыдущей осью времени, причем α < ⁠π/4⁠ . В новой системе отсчета одновременные события лежат параллельно линии, наклоненной на α к предыдущим линиям одновременности. Это новая ось x . Как исходный набор осей, так и заштрихованный набор осей обладают тем свойством, что они ортогональны относительно внутреннего произведения Минковского или релятивистского скалярного произведения . Исходное положение на вашей временной линии (ct) перпендикулярно положению A, исходному положению на вашей общей временной линии (x), где (t) равно нулю. Эта временная линия, где временные линии сходятся, затем располагается на одной и той же временной линии, даже когда есть 2 разных положения. 2 положения находятся на 45-градусной линии событий относительно исходного положения A. Следовательно, положение A и положение A' на линии событий и (t)=0, перемещаем A' обратно в положение A.

Какова бы ни была величина α , линия ct = x образует универсальную ^[4] биссектрису , как показано на рис. 2-2.

Часто встречаются диаграммы Минковского, где единицы измерения времени масштабируются с коэффициентом c таким образом, что одна единица x равна одной единице t . Такая диаграмма может иметь единицы

• Длина около 30 сантиметров и наносекунды
• Астрономические единицы и интервалы около 8 минут и 19 секунд (499 секунд)
• Световые годы и годы
• Световая секунда и вторая

При этом пути света представляются линиями, параллельными биссектрисе между осями.

Математические подробности

Рис. 2-3 Различные масштабы по осям.

Угол α между осями x и x ′ будет идентичен углу между осями времени ct и ct ′ . Это следует из второго постулата специальной теории относительности, который гласит, что скорость света одинакова для всех наблюдателей, независимо от их относительного движения (см. ниже). Угол α определяется по формуле ^[5]

${\displaystyle \tan \alpha ={\frac {v}{c}}=\beta .}$

Соответствующее увеличение от x и t до x ′ и t ′ и наоборот математически описывается преобразованием Лоренца , которое можно записать

${\displaystyle {\begin{aligned}ct'&=\gamma (ct-\beta x),\\x'&=\gamma (x-\beta ct)\\\end{aligned}}}$

где - фактор Лоренца . Применяя преобразование Лоренца, оси пространства-времени, полученные для усиленной системы отсчета, всегда будут соответствовать сопряженным диаметрам пары гипербол . ${\textstyle \gamma =\left(1-\beta ^{2}\right)^{-{\frac {1}{2}}}}$

Как показано на рис. 2-3, усиленные и не усиленные оси пространства-времени в общем случае будут иметь неравные единичные длины. Если U — единичная длина на осях ct и x соответственно, единичная длина на осях ct ′ и x ′ равна: ^[6]

${\displaystyle U'=U{\sqrt {\frac {1+\beta ^{2}}{1-\beta ^{2}}}}\,.}$

Ось ct представляет собой мировую линию часов, покоящихся в S , где U представляет собой длительность между двумя событиями, происходящими на этой мировой линии, также называемую собственным временем между этими событиями. Длина U на оси x представляет собой длину покоя или собственную длину стержня, покоящегося в S. Та же интерпретация может быть применена к расстоянию U ′ на осях ct ′ и x ′ для часов и стержней, покоящихся в S ′ .

История

Световой конус и гиперболы у Минковского (1908)

Альберт Эйнштейн объявил о своей специальной теории относительности в 1905 году ^[7] , а Герман Минковский представил ее графическое представление в 1908 году ^[8].

В статье Минковского 1908 года было три диаграммы, первая для иллюстрации преобразования Лоренца, затем разбиение плоскости световым конусом и, наконец, иллюстрация мировых линий. ^[8] Первая диаграмма использовала ветвь единичной гиперболы , чтобы показать геометрическое место единицы собственного времени в зависимости от скорости, тем самым иллюстрируя замедление времени. Вторая диаграмма показывала сопряженную гиперболу для калибровки пространства, где подобное растяжение оставляет впечатление сокращения Фицджеральда . В 1914 году Людвик Зильберштейн ^[9] включил диаграмму «представления Минковским преобразования Лоренца». Эта диаграмма включала единичную гиперболу, ее сопряженную и пару сопряженных диаметров . С 1960-х годов версия этой более полной конфигурации упоминается как Диаграмма Минковского и используется в качестве стандартной иллюстрации геометрии преобразования специальной теории относительности. ET Whittaker указал, что принцип относительности равносилен произвольности выбора радиуса гиперболы для времени в диаграмме Минковского. В 1912 году Гилберт Н. Льюис и Эдвин Б. Уилсон применили методы синтетической геометрии для разработки свойств неевклидовой плоскости, которая имеет диаграммы Минковского. ^{[10] [11]} ${\displaystyle t^{2}-x^{2}=1}$

Когда Тейлор и Уилер составили Spacetime Physics (1966), они не использовали термин диаграмма Минковского для своей геометрии пространства-времени. Вместо этого они включили признание вклада Минковского в философию через совокупность его инноваций 1908 года. ^[12]

Диаграммы Леделя

В то время как неподвижная система отсчета на диаграмме Минковского имеет ортогональные оси пространства-времени, система отсчета, движущаяся относительно неподвижной системы отсчета на диаграмме Минковского, имеет оси пространства-времени, которые образуют острый угол. Эта асимметрия диаграмм Минковского может вводить в заблуждение, поскольку специальная теория относительности постулирует, что любые две инерциальные системы отсчета должны быть физически эквивалентны. Диаграмма Леделя — это альтернативная диаграмма пространства-времени, которая делает симметрию инерциальных систем отсчета гораздо более очевидной.

Формулировка через срединную рамку

Несколько авторов показали, что существует система отсчета между покоящимися и движущимися, где их симметрия будет очевидна («срединная система»). ^[13] В этой системе две другие системы движутся в противоположных направлениях с одинаковой скоростью. Использование таких координат делает единицы длины и времени одинаковыми для обеих осей. Если β = ⁠в/с⁠ иданы междуи, то эти выражения связаны со значениями в их медианной системе координат S ₀ следующим образом: ^{[13] [14]} ${\textstyle \gamma =\left(1-\beta ^{2}\right)^{-{\frac {1}{2}}}}$ ${\displaystyle S}$ ${\displaystyle S^{\prime }}$

${\displaystyle {\begin{aligned}&(1)&\beta &={\frac {2\beta _{0}}{1+{\beta _{0}}^{2}}},\\[3pt]&(2)&\beta _{0}&={\frac {\gamma -1}{\beta \gamma }}.\end{aligned}}}$

Например, если β = 0,5 между и , то по (2) они движутся в своей средней системе отсчета S ₀ примерно со скоростью ±0,268 c каждая в противоположных направлениях. С другой стороны, если β ₀ = 0,5 в S ₀ , то по (1) относительная скорость между и в их собственных системах покоя составляет 0,8 c . Построение осей и выполняется в соответствии с обычным методом с использованием tan α = β ₀ относительно ортогональных осей средней системы отсчета (рис. 3-1). ${\displaystyle S}$ ${\displaystyle S^{\prime }}$ ${\displaystyle S}$ ${\displaystyle S^{\prime }}$ ${\displaystyle S}$ ${\displaystyle S^{\prime }}$

Однако оказывается, что при построении такой симметричной диаграммы можно вывести соотношения диаграммы, даже не упоминая медианную систему отсчета и β ₀ вообще. Вместо этого относительная скорость β = ⁠в/с⁠ междуиможет быть напрямую использовано в следующей конструкции, обеспечивая тот же результат: ^[15] ${\displaystyle S}$ ${\displaystyle S^{\prime }}$

Если φ — угол между осями ct ′ и ct (или между x и x ′ ), а θ — между осями x ′ и ct ′ , то получается: ^{[15] [16] [17] [18]}

${\displaystyle {\begin{aligned}\sin \varphi =\cos \theta &=\beta ,\\\cos \varphi =\sin \theta &={\frac {1}{\gamma }},\\\tan \varphi =\cot \theta &=\beta \gamma .\end{aligned}}}$

Из рис. 3-2 очевидны два способа построения: ось x проведена перпендикулярно оси ct ′ , оси x ′ и ct добавлены под углом φ ; и ось x ′ проведена под углом θ относительно оси ct ′ , ось x добавлена ​​перпендикулярно оси ct ′ , а ось ct перпендикулярна оси x ′ .

В диаграмме Минковского длины на странице не могут быть напрямую сопоставлены друг с другом из-за коэффициента деформации между единичными длинами осей в диаграмме Минковского. В частности, если и являются единичными длинами осей покоящейся системы координат и осей подвижной системы координат соответственно в диаграмме Минковского, то две единичные длины деформируются относительно друг друга по формуле: ${\displaystyle U}$ ${\displaystyle U^{\prime }}$

${\displaystyle U^{\prime }=U{\sqrt {\frac {1+\beta ^{2}}{1-\beta ^{2}}}}}$

Напротив, в симметричной диаграмме Леделя обе оси кадра и деформированы на один и тот же коэффициент относительно медианного кадра и, следовательно, имеют одинаковые длины единиц. Это подразумевает, что для пространственно-временной диаграммы Леделя мы можем напрямую сравнивать длины пространства-времени между различными кадрами, как они появляются на странице; масштабирование/преобразование длины единиц между кадрами не требуется из-за симметричной природы диаграммы Леделя. ${\displaystyle S}$ ${\displaystyle S^{\prime }}$

История

• Макс Борн (1920) нарисовал диаграммы Минковского, расположив ось ct ′ почти перпендикулярно оси x , а также ось ct к оси x ′ , чтобы продемонстрировать сокращение длины и замедление времени в симметричном случае двух стержней и двух часов, движущихся в противоположных направлениях. ^[19]
• Дмитрий Мириманов (1921) показал, что всегда существует срединная система отсчета относительно двух относительно движущихся систем отсчета, и вывел соотношения между ними из преобразования Лоренца. Однако он не дал графического представления в виде диаграммы. ^[13]
• Симметричные диаграммы были систематически разработаны Полом Грунером в сотрудничестве с Йозефом Заутером в двух статьях в 1921 году. Они продемонстрировали релятивистские эффекты, такие как сокращение длины и замедление времени, а также некоторые связи с ковариантными и контравариантными векторами. ^{[16] [17]} Грунер расширил этот метод в последующих статьях (1922–1924) и также отдал должное трактовке Мириманова. ^{[20] [21] [22] [23] [24] [25]}
• Построение симметричных диаграмм Минковского было позже независимо переоткрыто несколькими авторами. Например, начиная с 1948 года, Энрике Лёдель Палумбо опубликовал серию статей на испанском языке, в которых представил детали такого подхода. ^{[26] [27]} В 1955 году Анри Амар также опубликовал статью, в которой представил такие соотношения, и отдал должное Лёделю в последующей статье в 1957 году. ^{[28] [29]} Некоторые авторы учебников используют симметричные диаграммы Минковского, обозначая их как диаграммы Лёделя . ^{[15] [18]}

Релятивистские явления в диаграммах

Замедление времени

Рис 4-1. Релятивистское замедление времени, изображенное на двух пространственно-временных диаграммах Леделя. Оба наблюдателя считают, что часы другого идут медленнее.

Рис 4-2. Релятивистское замедление времени, изображенное на одной пространственно-временной диаграмме Леделя. Оба наблюдателя считают, что часы друг друга идут медленнее.

Релятивистское замедление времени относится к тому факту, что часы (показывающие свое собственное время в своей системе покоя), которые движутся относительно наблюдателя, как правило, идут медленнее. Ситуация изображена на симметричных диаграммах Леделя на рис. 4-1. Обратите внимание, что мы можем сравнивать длины пространства-времени на странице напрямую друг с другом из-за симметричной природы диаграммы Леделя.

На рис. 4-2 предполагается, что наблюдатель, чья система отсчета задана черными осями, движется от начала координат O к A. Движущиеся часы имеют систему отсчета, заданную синими осями, и движутся от O к B. Для черного наблюдателя все события, происходящие одновременно с событием в точке A, расположены на прямой линии, параллельной его пространственной оси. Эта линия проходит через A и B, поэтому A и B одновременны из системы отсчета наблюдателя с черными осями. Однако часы, которые движутся относительно черного наблюдателя, отсчитывают время вдоль синей оси времени. Это представлено расстоянием от O до B. Поэтому наблюдатель в точке A с черными осями замечает, что его часы показывают расстояние от O до A, в то время как он наблюдает, как часы движутся относительно него или нее, чтобы отсчитать расстояние от O до B. Поскольку расстояние от O до B меньше расстояния от O до A, они приходят к выводу, что время, прошедшее на часах, движущихся относительно них, меньше, чем время, прошедшее на их собственных часах.

Второй наблюдатель, переместившись вместе с часами из О в В, будет утверждать, что часы черной оси достигли только С и поэтому идут медленнее. Причиной этих, казалось бы, парадоксальных утверждений является различное определение событий, происходящих синхронно в разных местах. В силу принципа относительности вопрос о том, кто прав, не имеет ответа и не имеет смысла.

Сокращение длины

Рис 4-3 Релятивистское сокращение длины, как показано на двух диаграммах пространства-времени Леделя. Оба наблюдателя считают объекты, движущиеся вместе с другим наблюдателем, более короткими.

Рис 4-4 Релятивистское сокращение длины, как показано на одной пространственно-временной диаграмме Леделя. Оба наблюдателя считают объекты, движущиеся вместе с другим наблюдателем, более короткими.

Релятивистское сокращение длины относится к тому факту, что линейка (указывающая ее собственную длину в ее системе покоя), которая движется относительно наблюдателя, как наблюдается, сокращается/укорачивается. Ситуация изображена на симметричных диаграммах Леделя на рис. 4-3. Обратите внимание, что мы можем сравнивать длины пространства-времени на странице напрямую друг с другом из-за симметричной природы диаграммы Леделя.

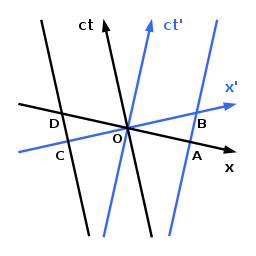
На рис. 4-4 снова предполагается, что наблюдатель движется вдоль оси ct . Предполагается, что мировые линии конечных точек объекта, движущегося относительно него, движутся вдоль оси ct ′ и параллельной линии, проходящей через A и B. Для этого наблюдателя конечными точками объекта в момент времени t = 0 являются O и A. Для второго наблюдателя, движущегося вместе с объектом, так что для него объект находится в состоянии покоя, он имеет собственную длину OB в момент времени t ′ = 0. Вследствие OA < OB объект сокращается для первого наблюдателя.

Второй наблюдатель будет утверждать, что первый наблюдатель оценил конечные точки объекта в O и A соответственно и, следовательно, в разное время, что приводит к неверному результату из-за его движения в это время. Если второй наблюдатель исследует длину другого объекта с конечными точками, движущимися вдоль оси ct и параллельной линии, проходящей через C и D, он заключает таким же образом, что этот объект должен быть сокращен от OD до OC. Каждый наблюдатель оценивает объекты, движущиеся с другим наблюдателем, как сокращенные. Эта, по-видимому, парадоксальная ситуация снова является следствием относительности одновременности, как показано анализом с помощью диаграммы Минковского.

Принимая все эти соображения во внимание, предполагалось, что оба наблюдателя принимают во внимание скорость света и расстояние до всех событий, которые они видят, чтобы определить фактическое время, в которое эти события происходят с их точки зрения.

Постоянство скорости света

Рис 4-5 Диаграмма Минковского для 3 систем координат. Для скоростей относительно системы в черном выполняется v ′ = 0,4 c и v ″ = 0,8 c .

Другой постулат специальной теории относительности — постоянство скорости света. Он гласит, что любой наблюдатель в инерциальной системе отсчета, измеряющий вакуумную скорость света относительно себя, получает одно и то же значение независимо от своего собственного движения и движения источника света. Это утверждение кажется парадоксальным, но оно немедленно следует из дифференциального уравнения, дающего это, и диаграмма Минковского согласуется с ним. Это также объясняет результат эксперимента Майкельсона–Морли , который считался загадкой до открытия теории относительности, когда считалось, что фотоны — это волны в необнаружимой среде.

Для мировых линий фотонов, проходящих через начало координат в разных направлениях, выполняется x = ct и x = − ct . Это означает, что любое положение на такой мировой линии соответствует шагам на осях x и ct одинаковой абсолютной величины. Из правила отсчета координат в системе координат с наклонными осями следует, что две мировые линии являются биссектрисами углов осей x и ct . Как показано на рис. 4-5, диаграмма Минковского иллюстрирует их как биссектрисы углов осей x′ и ct ′ . Это означает, что оба наблюдателя измеряют одну и ту же скорость c для обоих фотонов.

К этой диаграмме Минковского можно добавить дополнительные системы координат, соответствующие наблюдателям с произвольными скоростями. Для всех этих систем обе мировые линии фотонов представляют собой биссектрисы углов осей. Чем больше относительная скорость приближается к скорости света, тем больше оси приближаются к соответствующей биссектрисе угла. Ось всегда более плоская, а ось времени более крутая, чем мировые линии фотонов. Масштабы на обеих осях всегда идентичны, но обычно отличаются от масштабов других систем координат. ${\displaystyle x}$

Скорость света и причинность

Рис 4-6 Прошлое и будущее относительно начала координат. Для серых областей соответствующая временная классификация невозможна.

Прямые линии, проходящие через начало координат, которые круче, чем обе мировые линии фотонов, соответствуют объектам, движущимся медленнее скорости света. Если это применимо к объекту, то это применимо и с точки зрения всех наблюдателей, поскольку мировые линии этих фотонов являются биссектрисами углов для любой инерциальной системы отсчета. Следовательно, любая точка выше начала координат и между мировыми линиями обоих фотонов может быть достигнута со скоростью, меньшей скорости света, и может иметь причинно-следственную связь с началом координат. Эта область является абсолютным будущим, поскольку любое событие там происходит позже по сравнению с событием, представленным началом координат, независимо от наблюдателя, что наглядно видно из диаграммы Минковского на рис. 4-6.

Следуя тому же аргументу, область ниже начала координат и между мировыми линиями фотона является абсолютным прошлым относительно начала координат. Любое событие там определенно принадлежит прошлому и может быть причиной следствия в начале координат.

Связь между любыми такими парами событий называется времениподобной , потому что они имеют временное расстояние больше нуля для всех наблюдателей. Прямая линия, соединяющая эти два события, всегда является осью времени возможного наблюдателя, для которого они происходят в одном и том же месте. Два события, которые можно связать только скоростью света, называются светоподобными .

В принципе, к диаграмме Минковского можно добавить еще одно измерение пространства, что приведет к трехмерному представлению. В этом случае области будущего и прошлого становятся конусами с вершинами, касающимися друг друга в начале координат. Они называются световыми конусами .

Скорость света как предел

Рис 4-7 Отправка сообщения со сверхсветовой скоростью из O через A в B в прошлое. Оба наблюдателя считают временной порядок пар событий O и A, а также A и B различным.

Следуя тому же аргументу, все прямые линии, проходящие через начало координат и более горизонтальные, чем мировые линии фотона, будут соответствовать объектам или сигналам, движущимся быстрее света , независимо от скорости наблюдателя. Следовательно, ни одно событие за пределами световых конусов не может быть достигнуто из начала координат, даже световым сигналом, или любым объектом или сигналом, движущимся со скоростью, меньшей скорости света. Такие пары событий называются пространственноподобными , потому что они имеют конечное пространственное расстояние, отличное от нуля для всех наблюдателей. С другой стороны, прямая линия, соединяющая такие события, всегда является пространственной координатной осью возможного наблюдателя, для которого они происходят в одно и то же время. Небольшим изменением скорости этой системы координат в обоих направлениях всегда можно найти две инерциальные системы отсчета, наблюдатели которых оценивают хронологический порядок этих событий как разный.

Если объект движется быстрее света, скажем, из точки O в точку A на рис. 4-7, то для любого наблюдателя, наблюдающего за объектом, движущимся из точки O в точку A, можно найти другого наблюдателя (движущегося со скоростью, меньшей скорости света по отношению к первому), для которого объект движется из точки A в точку O. Вопрос о том, какой наблюдатель прав, не имеет однозначного ответа и, следовательно, не имеет физического смысла. Любой такой движущийся объект или сигнал нарушил бы принцип причинности.

Кроме того, любые общие технические средства отправки сигналов быстрее света позволят отправлять информацию в прошлое отправителя. На схеме наблюдатель в точке O в системе x - ct отправляет сообщение, движущееся быстрее света, в точку A. В точке A его получает другой наблюдатель, движущийся так, чтобы оказаться в системе x ′- ct ′ , который отправляет его обратно, снова быстрее света, в точку B. Но B находится в прошлом относительно O. Абсурдность этого процесса становится очевидной, когда оба наблюдателя впоследствии подтверждают, что они вообще не получали никакого сообщения, но все сообщения были направлены другому наблюдателю, как это можно графически увидеть на схеме Минковского. Более того, если бы можно было ускорить наблюдателя до скорости света, их пространственные и временные оси совпали бы с их биссектрисой угла. Система координат разрушилась бы в соответствии с тем фактом, что из-за замедления времени время фактически прекратило бы течь для них.

Эти соображения показывают, что скорость света как предел является следствием свойств пространства-времени, а не свойств объектов, таких как технологически несовершенные космические корабли. Запрет на движение со скоростью, превышающей скорость света, таким образом, не имеет ничего общего с электромагнитными волнами или светом, а является следствием структуры пространства-времени.

Ускоряющиеся наблюдатели

Рис. 5-1 Мгновенно сопутствующие системы отсчета ускоряющейся частицы, наблюдаемые из неподвижной системы отсчета.

Рис. 5-2 Мгновенно сопутствующие инерциальные системы отсчета вдоль мировой линии быстро ускоряющегося наблюдателя (начало координат).

Часто ошибочно утверждается, что специальная теория относительности не может справиться с ускоряющимися частицами или ускоряющимися системами отсчета. В действительности ускоряющиеся частицы не представляют никакой трудности в специальной теории относительности. С другой стороны, ускоряющиеся системы отсчета требуют особого подхода. Однако, пока мы имеем дело с плоским пространством-временем Минковского, специальная теория относительности может справиться с ситуацией. Общая теория относительности требуется только при наличии гравитации. ^[30]

4-векторное ускорение ускоряющейся частицы является производной по собственному времени ее 4-скорости. Это несложная ситуация для обработки. Ускоряющиеся системы отсчета требуют понимания концепции мгновенно сопутствующей системы отсчета (MCRF), то есть системы отсчета, движущейся с той же мгновенной скоростью, что и частица в любой заданный момент.

Рассмотрим анимацию на рис. 5-1. Изогнутая линия представляет собой мировую линию частицы, которая испытывает непрерывное ускорение, включая полное изменение направления в положительном и отрицательном направлениях x. Красные оси являются осями MCRF для каждой точки вдоль траектории частицы. Координаты событий в нештрихованной (стационарной) системе отсчета могут быть связаны с их координатами в любой мгновенно сопутствующей штрихованной системе отсчета с помощью преобразований Лоренца.

Рис. 5-2 иллюстрирует изменение видов пространства-времени вдоль мировой линии быстро ускоряющейся частицы. Ось (не нарисована) вертикальна, а ось (не нарисована) горизонтальна. Пунктирная линия — это пространственно-временная траектория («мировая линия») частицы. Шарики размещены через регулярные интервалы собственного времени вдоль мировой линии. Сплошные диагональные линии — это световые конусы для текущего события наблюдателя, и они пересекаются в этом событии. Маленькие точки — это другие произвольные события в пространстве-времени. ${\displaystyle ct'}$ ${\displaystyle x'}$

Наклон мировой линии (отклонение от вертикали) — это скорость частицы на этом участке мировой линии. Изгибы мировой линии представляют ускорение частицы. По мере ускорения частицы ее вид пространства-времени меняется. Эти изменения в видении управляются преобразованиями Лоренца. Также обратите внимание, что:

• шарики на мировой линии до/после будущих/прошлых ускорений разнесены на большее расстояние из-за замедления времени.
• события, которые были одновременными до ускорения (горизонтально разнесенные события), впоследствии происходят в разное время из-за относительности одновременности,
• события проходят через линии светового конуса из-за хода собственного времени, а не из-за изменения вида, вызванного ускорениями, и
• мировая линия всегда остается внутри будущего и прошлого световых конусов текущего события.

Если представить каждое событие как вспышку света, то события, которые находятся в пределах светового конуса прошлого наблюдателя, являются событиями, видимыми наблюдателю. Наклон мировой линии (отклонение от вертикали) дает скорость относительно наблюдателя.

Случай неинерциальных систем отсчета

Рис 6-1 Диаграмма Минковского в инерциальной системе отсчета. Слева — вертикальная мировая линия падающего объекта. Справа — гиперболическая мировая линия ракеты.

Рис 6-2 Диаграмма Минковского в неинерциальной системе отсчета. Слева — мировая линия падающего объекта. Справа — вертикальная мировая линия ракеты.

Мировые линии фотона определяются с помощью метрики с . ^[31] Световые конусы деформируются в соответствии с положением. В инерциальной системе отсчета свободная частица имеет прямую мировую линию. В неинерциальной системе отсчета мировая линия свободной частицы искривлена. ${\displaystyle d\tau =0}$

Давайте рассмотрим пример падения объекта, сброшенного без начальной скорости с ракеты. Ракета имеет равномерно ускоренное движение относительно инерциальной системы отсчета. Как видно из рис. 6-2 диаграммы Минковского в неинерциальной системе отсчета, объект, однажды сброшенный, набирает скорость, достигает максимума, а затем его скорость уменьшается и асимптотически сокращается на горизонте, где его собственное время застывает в . Скорость измеряется наблюдателем, находящимся в состоянии покоя в ускоренной ракете. ${\displaystyle t_{\text{H}}}$

Смотрите также

• Физический портал

• пространство Минковского
• Диаграмма Пенроуза
• Быстрота

Ссылки

1. "Что такое графики зависимости положения от времени?". Khan Academy . Получено 19 ноября 2018 г.
2. Коллиер, Питер (2017). Самое непостижимое: заметки к очень деликатному введению в математику относительности (3-е изд.). Непостижимые книги. ISBN 9780957389465.
3. Мермин (1968) Глава 17
4. См . Владимир Карапетов
5. Демтрёдер, Вольфганг (2016). Механика и термодинамика (иллюстрированное издание). Springer. С. 92–93. ISBN 978-3-319-27877-3.Выдержка из страницы 93
6. Фройнд, Юрген (2008). Специальная теория относительности для начинающих: учебник для студентов . World Scientific. стр. 49. ISBN 978-9812771599.
7. Эйнштейн, Альберт (1905). "Zur Elektrodynamic bewegter Körper" [К электродинамике движущихся тел] (PDF) . Аннален дер Физик . 322 (10): 891–921. Бибкод : 1905АнП...322..891Е. дои : 10.1002/andp.19053221004 .. См. также: перевод на английский язык.
8. Минковский, Герман (1909). «  Raum und Zeit» [Пространство и время]. Physikalische Zeitschrift . 10 : 75–88.

   Различные переводы на английский язык на Wikisource: Space and Time

9. Зильберштейн, Людвик (1914). Теория относительности. стр. 131.
10. Уилсон, Эдвин Б.; Льюис , Гилберт Н. (1912). «Пространственно-временное многообразие относительности. Неевклидова геометрия механики и электромагнетизма». Труды Американской академии искусств и наук . 48 (11): 387–507. doi :10.2307/20022840. JSTOR  20022840.
11. Синтетическое пространство-время, сборник аксиом, использованных Уилсоном и Льюисом, и доказанных теорем. Архивировано WebCite
12. Тейлор, Эдвин Ф.; Уилер (1966). Физика пространства-времени . Сан-Франциско: WH Freeman. стр. 37. Прозрение Минковского является центральным для понимания физического мира. Оно фокусирует внимание на таких величинах, как интервал, которые одинаковы во всех системах отсчета. Оно выявляет относительный характер величин, таких как скорость, энергия, время, расстояние, которые зависят от системы отсчета.
13. Мириманов, Дмитрий (1921). «Преобразование Лоренца-Эйнштейна и вселенских времен М. Эда Гийома». Archives des Sciences Physiques et Naturelles (Приложение) . 5. 3 : 46–48.(Перевод: Преобразование Лоренца-Эйнштейна и универсальное время Эд. Гийома)
14. Shadowitz, Albert (2012). Электромагнитное поле (переиздание издания 1975 года). Courier Dover Publications. стр. 460. ISBN 978-0486132013.См. Google книги, стр. 460
15. Сартори, Лео (1996). Понимание относительности: упрощенный подход к теориям Эйнштейна . Издательство Калифорнийского университета. С. 151 и далее. ISBN 0-520-20029-2.
16. Грунер, Пол; Заутер, Йозеф (1921). «Элементарное геометрическое представление формул теории относительности». Архивы естественных и физических наук . 5. 3 : 295–296.(Перевод: Элементарное геометрическое представление формул специальной теории относительности)
17. Грюнер, Пол (1921). «Eine elementare geometrische Darstellung der Transformationsformeln der speziellen Relativitätstheorie» [Элементарное геометрическое представление формул преобразования специальной теории относительности]. Physikalische Zeitschrift . 22 : 384–385.(перевод: Элементарное геометрическое представление формул преобразований специальной теории относительности)
18. Shadowitz, Albert (1988). Специальная теория относительности (переиздание издания 1968 года). Courier Dover Publications. стр. 20–22. ISBN 0-486-65743-4.
19. Борн, Макс (1920). Die Relativitätstheorie Einsteins [ Теория относительности Эйнштейна ]. Naturwissenschaftliche monographien und lehrbücher ... 3. Bd. (Первое изд.). Спрингер. стр. 177–180.См. также Переиздание (2013) третьего издания (1922) в Google Books, стр. 187
20. Грюнер, Пол (1922). Elemente der Relativitätstheorie [ Элементы теории относительности ]. Берн: П. Хаупт.
21. Грюнер, Пол (1922). «Graphische Darstellung der speziellen Relativitätstheorie in der vier Dimensionen Raum-Zeit-Welt I» [Графическое представление специальной теории относительности в четырехмерном мире пространства-времени I]. Zeitschrift für Physik . 10 (1): 22–37. Бибкод : 1922ZPhy...10...22G. дои : 10.1007/BF01332542. S2CID  123131527.
22. Грюнер, Пол (1922). «Graphische Darstellung der speziellen Relativitätstheorie in der vier Dimensionen Raum-Zeit-Welt II» [Графическое представление специальной теории относительности в четырехмерном мире пространства-времени II]. Zeitschrift für Physik . 10 (1): 227–235. Бибкод : 1922ZPhy...10..227G. дои : 10.1007/BF01332563. S2CID  186220809.
23. Грюнер, Пол (1921). «а) Графическое представление космических времен вселенных в четырех измерениях. б) Графическое представление временных вселенных в теории относительности» [а) Графическое представление четырехмерной вселенной пространства-времени. б) Графическое изображение всемирного времени в теории относительности. Архивы естественных и физических наук . 5. 4 : 234–236.(перевод: Графическое представление четырехмерной пространственно-временной вселенной)
24. Грюнер, Пол (1922). «Die Bedeutung «reduzierter» ортогональная система координат для тензорного анализа и специальной теории относительности». Zeitschrift für Physik . 10 (1): 236–242. Бибкод : 1922ZPhy...10..236G. дои : 10.1007/BF01332564. S2CID  120593068.
25. Грюнер, Пол (1924). «Geometrische Darstellungen der speziellen Relativitätstheorie, insbesondere des elektromagnetischen Feldes bewegter Körper» [Геометрические представления специальной теории относительности, в частности электромагнитного поля движущихся тел]. Zeitschrift für Physik . 21 (1): 366–371. Бибкод : 1924ZPhy...21..366G. дои : 10.1007/BF01328285. S2CID  121376032.
26. Ледель, Энрике (1948). «Aberración y Relatividad» [Аберрация и относительность]. Аналитики научного общества Аргентины . 145 : 3–13.
27. Fisica relativista , Kapelusz Editorial, Буэнос-Айрес, Аргентина (1955).
28. Амар, Анри (1955). «Новое геометрическое представление преобразования Лоренца». American Journal of Physics . 23 (8): 487–489. Bibcode : 1955AmJPh..23..487A. doi : 10.1119/1.1934074.
29. Амар, Анри; Лёдель, Энрике (1957). «Геометрическое представление преобразования Лоренца». Американский журнал физики . 25 (5): 326–327. Bibcode : 1957AmJPh..25..326A. doi : 10.1119/1.1934453.
30. Гиббс, Филип. «Может ли специальная теория относительности справиться с ускорением?». Оригинальный Usenet Physics FAQ . Калифорнийский университет, Риверсайд . Получено 6 ноября 2021 г.
31. Руо, Матье (2021). Специальная теория относительности, геометрический подход: курс с упражнениями и ответами, за которым следует конференция «Межзвездные путешествия и антиматерия» (PDF) . Querrien: Mathieu Rouaud. стр. 534. ISBN 978-2-9549309-3-0.

• French, AP (1968). Специальная теория относительности . Вводная серия по физике Массачусетского технологического института. Нью-Йорк: Norton [ua] стр. 82–83. ISBN 978-0-17-177075-9.
• Glass, EN (1975-11-01). «Ускорения Лоренца и диаграммы Минковского». American Journal of Physics . 43 (11): 1013–1014. Bibcode : 1975AmJPh..43.1013G. doi : 10.1119/1.9953. ISSN  0002-9505.
• Мермин, Н. Дэвид (1968). "17: Диаграммы Минковского: Геометрия пространства-времени". Пространство и время в специальной теории относительности. Нью-Йорк: McGraw-Hill. стр. 155-199.
• Риндлер, Вольфганг (2001). Относительность: специальная, общая и космологическая (2-е изд.). Oxford University Press. ISBN 978-0-19-856732-5.
• Россер, Уильям Г. В. (1971). Введение в теорию относительности (3-е изд., ред.). Лондон: Баттерворт. стр. 256, рис. 6.4. ISBN 978-0-408-55700-9.
• Тейлор, Эдвин Ф.; Уилер, Джон Арчибальд (2003). Физика пространства-времени: введение в специальную теорию относительности (PDF) (2-е изд., 9-е печатное изд.). Нью-Йорк, Нью-Йорк: WH Freeman. ISBN 978-0-7167-2327-1.
• Уолтер, Скотт (1999-07-22). "Неевклидов стиль теории относительности Минковского" (PDF) . В Грей, Джереми (ред.). Символическая Вселенная. Oxford University PressOxford. стр. 91–127. doi :10.1093/oso/9780198500889.003.0007. ISBN 978-0-19-850088-9. Архивировано из оригинала (PDF) 2013-10-16 . Получено 2011-03-27 .{{cite book}}: CS1 maint: date and year (link)(см. стр. 10 электронной ссылки)

Внешние ссылки

Медиафайлы по теме Диаграммы Минковского на Wikimedia Commons