Системная динамика

Изучение нелинейных сложных систем

Динамическая диаграмма запасов и потоков модели «Принятие нового продукта» (модель из статьи Джона Стермана 2001 г. - True Software)

Системная динамика ( SD ) — это подход к пониманию нелинейного поведения сложных систем с течением времени с использованием запасов, потоков , внутренних контуров обратной связи , табличных функций и временных задержек. ^[1]

Обзор

Системная динамика — это методология и метод математического моделирования для формулирования, понимания и обсуждения сложных вопросов и проблем. Первоначально разработанная в 1950-х годах для того, чтобы помочь корпоративным менеджерам улучшить свое понимание промышленных процессов, в настоящее время SD используется в государственном и частном секторе для анализа и разработки политики. ^[2]

Удобный графический интерфейс пользователя (GUI) системного программного обеспечения динамики, разработанного в удобные для пользователя версии к 1990-м годам и применяемого к различным системам. Модели SD решают проблему одновременности (взаимной причинности) путем обновления всех переменных с небольшими временными приращениями с положительными и отрицательными обратными связями и временными задержками, структурирующими взаимодействия и контроль. Самая известная модель SD, вероятно, это « Пределы роста» 1972 года . Эта модель предсказывает, что экспоненциальный рост населения и капитала с конечными источниками и стоками ресурсов и задержками восприятия приведет к экономическому коллапсу в 21 веке при самых разных сценариях роста.

Системная динамика — это аспект теории систем как метод понимания динамического поведения сложных систем. Основой метода является признание того, что структура любой системы, множество круговых, взаимосвязанных, иногда отсроченных во времени отношений между ее компонентами, часто так же важны для определения ее поведения, как и сами отдельные компоненты. Примерами являются теория хаоса и социальная динамика . Также утверждается, что поскольку часто существуют свойства целого, которые нельзя найти среди свойств элементов, в некоторых случаях поведение целого нельзя объяснить с точки зрения поведения частей.

История

Системная динамика была создана в середине 1950-х годов ^[3] профессором Джеем Форрестером из Массачусетского технологического института . В 1956 году Форрестер принял должность профессора в недавно сформированной Школе менеджмента имени Слоуна при Массачусетском технологическом институте . Его первоначальной целью было определить, как его опыт в науке и инженерии может быть использован каким-либо полезным образом для решения основных вопросов, определяющих успех или неудачу корпораций. Понимание Форрестером общих основ, лежащих в основе инженерии, которое привело к созданию системной динамики, было в значительной степени вызвано его взаимодействием с менеджерами General Electric (GE) в середине 1950-х годов. В то время менеджеры GE были озадачены, поскольку занятость на их заводах по производству бытовой техники в Кентукки демонстрировала значительный трехлетний цикл. Бизнес-цикл был признан недостаточным объяснением нестабильности занятости. С помощью ручного моделирования (или расчетов) структуры запасов-потоков-обратной связи заводов GE, которая включала существующую корпоративную структуру принятия решений по найму и увольнениям, Forrester смог показать, что нестабильность занятости в GE была обусловлена ​​внутренней структурой фирмы, а не внешней силой, такой как деловой цикл. Эти ручные моделирования стали началом области системной динамики. ^[2]

В конце 1950-х и начале 1960-х годов Форрестер и группа аспирантов переместили зарождающуюся область системной динамики со стадии ручного моделирования на стадию формального компьютерного моделирования . Ричард Беннетт создал первый язык компьютерного моделирования системной динамики под названием SIMPLE (Simulation of Industrial Management Problems with Lots of Equations) весной 1958 года. В 1959 году Филлис Фокс и Александр Пью написали первую версию DYNAMO (DYNAmic MODELS), улучшенную версию SIMPLE, и язык системной динамики стал отраслевым стандартом на более чем тридцать лет. Форрестер опубликовал первую и до сих пор классическую книгу в этой области под названием Industrial Dynamics в 1961 году . ^[2]

С конца 1950-х до конца 1960-х годов системная динамика применялась почти исключительно к корпоративным/управленческим проблемам. Однако в 1968 году неожиданное событие заставило эту область расшириться за пределы корпоративного моделирования. Джон Ф. Коллинз , бывший мэр Бостона, был назначен приглашенным профессором по городским вопросам в Массачусетском технологическом институте. Результатом сотрудничества Коллинза и Форрестера стала книга под названием « Городская динамика» . Модель городской динамики, представленная в книге, стала первым крупным некорпоративным применением системной динамики. ^[2] В 1967 году Ричард М. Гудвин опубликовал первое издание своей статьи «Цикл роста», ^[4], которая была первой попыткой применить принципы системной динамики к экономике. Он посвятил большую часть своей жизни преподаванию того, что он называл «Экономической динамикой», которую можно считать предшественником современной неравновесной экономики . ^[5]

Второе крупное некорпоративное применение системной динамики появилось вскоре после первого. В 1970 году Джей Форрестер был приглашен Римским клубом на встречу в Берне, Швейцария. Римский клуб — это организация, посвященная решению того, что ее члены описывают как «затруднительное положение человечества», то есть глобального кризиса, который может возникнуть когда-нибудь в будущем из-за требований, предъявляемых к пропускной способности Земли (ее источникам возобновляемых и невозобновляемых ресурсов и ее стокам для утилизации загрязняющих веществ) экспоненциально растущим населением мира. На встрече в Берне Форрестеру был задан вопрос, можно ли использовать системную динамику для решения затруднительного положения человечества. Он, конечно же, ответил, что можно. На обратном пути со встречи в Берне Форрестер создал первый проект модели системной динамики мировой социально-экономической системы. Он назвал эту модель WORLD1. По возвращении в Соединенные Штаты Форрестер усовершенствовал WORLD1 в рамках подготовки к визиту в Массачусетский технологический институт членов Римского клуба. Forrester назвал усовершенствованную версию модели WORLD2. Forrester опубликовал WORLD2 в книге под названием World Dynamics . ^[2]

Темы по системной динамике

Основными элементами диаграмм системной динамики являются обратная связь, накопление потоков в запасах и временные задержки.

В качестве иллюстрации использования системной динамики представьте себе организацию, которая планирует ввести инновационный новый потребительский продукт длительного пользования. Организации необходимо понимать возможную динамику рынка, чтобы разрабатывать маркетинговые и производственные планы.

Диаграммы причинно-следственных связей

В методологии системной динамики проблема или система (например, экосистема, политическая система или механическая система) могут быть представлены в виде диаграммы причинно-следственной связи . ^[6] Диаграмма причинно-следственной связи — это простая карта системы со всеми ее составными компонентами и их взаимодействиями. Захватывая взаимодействия и, следовательно, петли обратной связи (см. рисунок ниже), диаграмма причинно-следственной связи раскрывает структуру системы. Понимая структуру системы, становится возможным установить поведение системы в течение определенного периода времени. ^[7]

Причинно-следственная диаграмма внедрения нового продукта может выглядеть следующим образом:

Диаграмма причинно-следственной связи модели принятия нового продукта

На этой диаграмме есть две петли обратной связи. Положительная петля подкрепления (обозначенная R) справа указывает на то, что чем больше людей уже приняли новый продукт, тем сильнее влияние «сарафанного радио». Будет больше ссылок на продукт, больше демонстраций и больше обзоров. Эта положительная обратная связь должна генерировать продажи, которые продолжают расти.

Вторая петля обратной связи слева — это отрицательное подкрепление (или «балансировка», поэтому она обозначена как B). Очевидно, что рост не может продолжаться вечно, потому что по мере того, как все больше людей принимают, остается все меньше и меньше потенциальных последователей.

Оба контура обратной связи действуют одновременно, но в разное время они могут иметь разную силу. Таким образом, можно ожидать роста продаж в первые годы, а затем снижения продаж в последующие годы. Однако, в общем, диаграмма причинно-следственной связи не определяет структуру системы в достаточной степени, чтобы позволить определить ее поведение только на основе визуального представления. ^[8]

Диаграммы запасов и потоков

Причинно-следственные диаграммы помогают визуализировать структуру и поведение системы, а также качественно анализировать систему. Для проведения более детального количественного анализа причинно-следственная диаграмма преобразуется в диаграмму запасов и потоков . Модель запасов и потоков помогает изучать и анализировать систему количественным способом; такие модели обычно строятся и моделируются с помощью компьютерного программного обеспечения.

Запас — это термин для любой сущности, которая накапливается или истощается с течением времени. Поток — это скорость изменения запаса.

Поток – это скорость накопления запаса

В этом примере есть два запаса: Потенциальные последователи и Адопторы. Есть один поток: Новые последователи. Для каждого нового последователя запас потенциальных последователей уменьшается на единицу, а запас последователей увеличивается на единицу.

Диаграмма запасов и потоков модели принятия нового продукта

Уравнения

Реальная мощь системной динамики используется посредством моделирования. Хотя моделирование можно выполнить в электронной таблице , существует множество программных пакетов, оптимизированных для этого.

Моделирование включает в себя следующие этапы:

• Определить границу проблемы
• Определите наиболее важные запасы и потоки, которые изменяют эти уровни запасов.
• Определите источники информации, которые влияют на потоки
• Определите основные циклы обратной связи
• Нарисуйте причинно-следственную диаграмму, которая связывает запасы, потоки и источники информации.
• Напишите уравнения, определяющие потоки
• Оцените параметры и начальные условия. Они могут быть оценены с использованием статистических методов, экспертного мнения, данных маркетинговых исследований или других соответствующих источников информации. ^[9]
• Смоделируйте модель и проанализируйте результаты.

В этом примере уравнения, которые изменяют два запаса посредством потока, следующие:

 ${\displaystyle \ {\mbox{Potential adopters}}=-\int _{0}^{t}{\mbox{New adopters }}\,dt}$ ${\displaystyle \ {\mbox{Adopters}}=\int _{0}^{t}{\mbox{New adopters }}\,dt}$

Уравнения в дискретном времени

Список всех уравнений в дискретном времени , в порядке их выполнения в каждом году, для годов с 1 по 15:

 ${\displaystyle 1)\ {\mbox{Probability that contact has not yet adopted}}={\mbox{Potential adopters}}/({\mbox{Potential adopters }}+{\mbox{ Adopters}})}$ ${\displaystyle 2)\ {\mbox{Imitators}}=q\cdot {\mbox{Adopters}}\cdot {\mbox{Probability that contact has not yet adopted}}}$ ${\displaystyle 3)\ {\mbox{Innovators}}=p\cdot {\mbox{Potential adopters}}}$ ${\displaystyle 4)\ {\mbox{New adopters}}={\mbox{Innovators}}+{\mbox{Imitators}}}$ ${\displaystyle 4.1)\ {\mbox{Potential adopters}}\ -={\mbox{New adopters }}}$ ${\displaystyle 4.2)\ {\mbox{Adopters}}\ +={\mbox{New adopters }}}$

 ${\displaystyle \ p=0.03}$ ${\displaystyle \ q=0.4}$

Результаты динамического моделирования

Результаты динамического моделирования показывают, что поведение системы будет заключаться в росте числа последователей , который следует классической форме s-кривой.
Рост числа последователей изначально очень медленный, затем в течение некоторого периода наблюдается экспоненциальный рост, за которым в конечном итоге следует насыщение.

Динамическая диаграмма запасов и потоков модели принятия нового продукта

Значения запасов и потоков за годы = от 0 до 15

Уравнения в непрерывном времени

Чтобы получить промежуточные значения и лучшую точность, модель может работать в непрерывном времени: мы умножаем количество единиц времени и пропорционально делим значения, которые изменяют уровни запасов. В этом примере мы умножаем 15 лет на 4, чтобы получить 60 кварталов, и делим значение потока на 4.
Деление значения является самым простым с помощью метода Эйлера , но вместо этого можно использовать другие методы, такие как методы Рунге–Кутты .

Список уравнений в непрерывном времени для триместров = от 1 до 60:

• Это те же уравнения, что и в разделе «Уравнения в дискретном времени» выше, за исключением уравнений 4.1 и 4.2, замененных следующими:

 ${\displaystyle 10)\ {\mbox{Valve New adopters}}\ ={\mbox{New adopters}}\cdot TimeStep}$ ${\displaystyle 10.1)\ {\mbox{Potential adopters}}\ -={\mbox{Valve New adopters}}}$ ${\displaystyle 10.2)\ {\mbox{Adopters}}\ +={\mbox{Valve New adopters }}}$

 ${\displaystyle \ TimeStep=1/4}$

• На приведенной ниже диаграмме запасов и потоков промежуточный поток «Новые пользователи клапана» рассчитывается по уравнению:

 ${\displaystyle \ {\mbox{Valve New adopters}}\ ={\mbox{New adopters }}\cdot TimeStep}$

Динамическая диаграмма запасов и потоков модели принятия нового продукта в непрерывном времени

Приложение

Системная динамика нашла применение в широком спектре областей, например , в народонаселении , сельском хозяйстве ^{[10] ,} экологических и экономических системах, которые обычно тесно взаимодействуют друг с другом.

Системная динамика имеет различные приложения управления "на обороте конверта". Они являются мощным инструментом для:

• Обучайте рефлексам системного мышления людей, проходящих коучинг
• Анализируйте и сравнивайте предположения и ментальные модели о том, как все работает
• Получите качественное представление о работе системы или последствиях решения
• Распознавать архетипы дисфункциональных систем в повседневной практике

Компьютерное программное обеспечение используется для моделирования модели системной динамики изучаемой ситуации. Запуск симуляций «что если» для проверки определенных политик на такой модели может значительно помочь в понимании того, как система изменяется с течением времени. Системная динамика очень похожа на системное мышление и строит те же диаграммы причинно-следственных связей систем с обратной связью. Однако системная динамика обычно идет дальше и использует симуляцию для изучения поведения систем и влияния альтернативных политик. ^[11]

Системная динамика использовалась для исследования зависимостей ресурсов и возникающих в результате проблем при разработке продукта. ^{[12] [13]}

Системно-динамический подход к макроэкономике , известный как подход Мински , был разработан экономистом Стивом Кином . ^[14] Он успешно использовался для моделирования мирового экономического поведения от кажущейся стабильности Великой умеренности до внезапного и неожиданного финансового кризиса 2007–2008 годов .

Пример: Рост и упадок компаний

Причинно-следственная диаграмма модели, изучающей рост или упадок компании по страхованию жизни. ^[15]

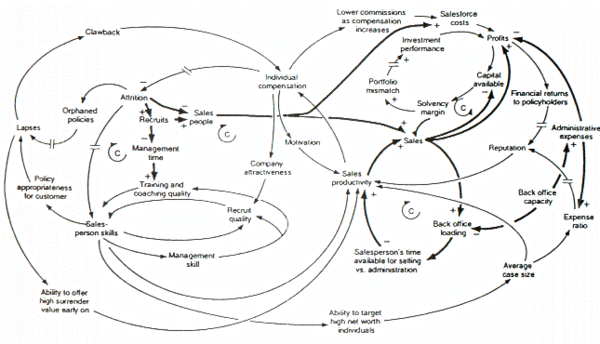
Рисунок выше представляет собой причинно-следственную диаграмму модели динамики системы, созданную для изучения сил, которые могут быть ответственны за рост или упадок компаний по страхованию жизни в Соединенном Королевстве . Стоит упомянуть ряд особенностей этого рисунка. Во-первых, отрицательные обратные связи модели обозначены буквами C , что означает противодействующие петли. Во-вторых, двойные косые черты используются для обозначения мест, где существует значительная задержка между причинами (т. е. переменными на концах стрелок) и следствиями (т. е. переменными на концах стрелок). Это распространенное соглашение о причинно-следственных диаграммах в динамике систем. В-третьих, более толстые линии используются для обозначения обратных связей и связей, на которых автор хочет, чтобы аудитория сосредоточилась. Это также распространенное соглашение о диаграммах динамики системы. Наконец, очевидно, что лицо, принимающее решения, не сможет продумать динамическое поведение, присущее модели, только изучив рисунок. ^[15]

Пример: Движение поршня

1. Цель: изучение системы кривошипно-шатунного механизма.
   Мы хотим смоделировать систему кривошипно-шатунного механизма с помощью динамической модели системы. Два различных полных описания физической системы с соответствующими системами уравнений можно найти здесь (на английском языке) и здесь (на французском языке) ; они дают одинаковые результаты. В этом примере кривошип с переменным радиусом и угловой частотой будет приводить в движение поршень с переменной длиной шатуна.
2. Системное динамическое моделирование: система теперь моделируется в соответствии с динамической логикой системы запасов и потоков.
   На рисунке ниже показана диаграмма запасов и потоков

   Схема запаса и потока для системы кривошипно-шатунного механизма

3. Моделирование: поведение динамической системы кривошипно-шатунного механизма может быть смоделировано.
   Следующий рисунок представляет собой 3D-моделирование, созданное с использованием процедурной анимации . Переменные модели анимируют все части этой анимации: кривошип, радиус, угловую частоту, длину шатуна и положение поршня.

Процедурная 3D -анимация кривошипно-шатунной системы, смоделированной в 2

Смотрите также

Ссылки

1. «Проект MIT по системной динамике в образовании (SDEP)».
2. Майкл Дж. Радзицкий и Роберт А. Тейлор (2008). «Происхождение системной динамики: Джей У. Форрестер и история системной динамики». В: Введение в системную динамику Министерства энергетики США . Получено 23 октября 2008 г.
3. Форрестер, Джей (1971). Контринтуитивное поведение социальных систем. Technology Review 73(3): 52–68
4. Гудвин, Р. М. (1982). Цикл роста. В: Очерки экономической динамики. Palgrave Macmillan, Лондон. [1]
5. Ди Маттео, М. и Сорди, С. (2015). Гудвин в Сиене: экономист, социальный философ и художник. Cambridge Journal of Economics, 39(6), 1507–1527. [2]
6. Стерман, Джон Д. (2000). Динамика бизнеса: системное мышление и моделирование для сложного мира . Бостон: McGraw-Hill. ISBN 0-07-231135-5.
7. Медоуз, Донелла. (2008). Системное мышление: Учебник. Earthscan
8. « Проблемы с диаграммами причинно-следственной связи». Syst. Dyn. Rev. 2 (2): 158–170. doi :10.1002/sdr.4260020207.
9. Стерман, Джон Д. (2001). «Моделирование динамики систем: инструменты для обучения в сложном мире». California Management Review . 43 (4): 8–25. doi :10.2307/41166098. JSTOR  41166098. S2CID  4637381.
10. FHA Rahim, NN Hawari и NZ Abidin, «Спрос и предложение риса в Малайзии: системно-динамический подход», Международный журнал по цепочке поставок и управлению, том 6, № 4, стр. 234-240, 2017.
11. Общество системной динамики
12. Репеннинг, Нельсон П. (2001). «Понимание пожаротушения при разработке новых продуктов» (PDF) . Журнал управления инновациями в области продуктов . 18 (5): 285–300. doi :10.1016/S0737-6782(01)00099-6. hdl : 1721.1/3961 .
13. Нельсон П. Репеннинг (1999). Зависимость от ресурсов в усилиях по улучшению разработки продукта , MIT Sloan School of Management Department of Operations Management/System Dynamics Group, декабрь 1999 г.
14.  [3] Минский - Проект месяца Январь 2014. Интервью с командой разработчиков Минский. Доступен в январе 2014 г.
15. Майкл Дж. Радзицкий и Роберт А. Тейлор (2008). "Обратная связь". В: Введение в системную динамику Министерства энергетики США . Получено 23 октября 2008 г.

Дальнейшее чтение

• Kypuros, Javier (2013). Системная динамика и управление с моделированием графа облигаций . Boca Raton: Taylor & Francis. ISBN 978-1466560758.
• Форрестер, Джей В. (1961). Промышленная динамика . Pegasus Communications. ISBN 978-1-883823-36-8.
• Форрестер, Джей В. (1969). Urban Dynamics . Pegasus Communications. ISBN 978-1-883823-39-9.
• Медоуз, Донелла Х. (1972). Пределы роста . Нью-Йорк: Университетские книги. ISBN 978-0-87663-165-2.
• Morecroft, John (2007). Стратегическое моделирование и динамика бизнеса: системный подход с обратной связью . John Wiley & Sons. ISBN 978-0-470-01286-4.
• Робертс, Эдвард Б. (1978). Управленческие приложения системной динамики . Кембридж: MIT Press. ISBN 978-0-262-18088-7.
• Рандерс, Йорген (1980). Элементы метода системной динамики . Кембридж: MIT Press. ISBN 978-0-915299-39-3.
• Сенге, Питер (1990). Пятая дисциплина . Валюта. ISBN 978-0-385-26095-4.
• Стерман, Джон Д. (2000). Бизнес-динамика: системное мышление и моделирование для сложного мира . McGraw Hill. ISBN 978-0-07-231135-8.

Внешние ссылки

• Общество системной динамики
• Исследование, подготовленное для Министерства энергетики США, посвящено введению системной динамики -
• Desert Island Dynamics «Аннотированный обзор основ системной динамики»
• True World: Temporal Reasoning Universal Elaboration: программное обеспечение System Dynamics, используемое для диаграмм в этой статье (бесплатно)