Обработка геометрии

Обработка полигональной сетки Марио Ботч и др. представляет собой учебник по теме «Обработка геометрии». ^[1]

Обработка геометрии — это область исследований, в которой используются концепции прикладной математики , информатики и инженерии для разработки эффективных алгоритмов получения, реконструкции , анализа , манипулирования, моделирования и передачи сложных 3D-моделей. Как следует из названия, многие концепции, структуры данных и алгоритмы напрямую аналогичны обработке сигналов и обработке изображений . Например, там, где сглаживание изображения может свертывать сигнал интенсивности с ядром размытия, сформированным с помощью оператора Лапласа , геометрическое сглаживание может быть достигнуто путем свертки геометрии поверхности с ядром размытия, сформированным с помощью оператора Лапласа-Бельтрами .

Приложения алгоритмов обработки геометрии уже охватывают широкий спектр областей: от мультимедиа , развлечений и классического компьютерного проектирования до биомедицинских вычислений, реверс-инжиниринга и научных вычислений . ^[1]

Обработка геометрии — распространенная тема исследований на SIGGRAPH , главной научной конференции по компьютерной графике , а также основная тема ежегодного симпозиума по обработке геометрии .

Обработка геометрии как жизненный цикл

Сетка кактуса, показывающая гауссову кривизну в каждой вершине с использованием метода угловых дефектов.

Обработка геометрии предполагает работу с формой , обычно в 2D или 3D, хотя форма может существовать в пространстве произвольных размеров. Обработка формы включает три этапа, которые называются ее жизненным циклом. При «рождении» форма может быть создана одним из трех методов: моделью , математическим представлением или сканированием . После рождения формы ее можно анализировать и редактировать несколько раз в цикле. Обычно это включает в себя получение различных измерений, таких как расстояния между точками формы, гладкость формы или ее эйлерова характеристика . Редактирование может включать шумоподавление, деформацию или выполнение жестких преобразований . На заключительном этапе «жизни» формы она расходуется. Это может означать, что он используется зрителем, например, как визуализируемый ресурс в игре или фильме. Конец жизни формы также может быть определен решением относительно формы, например, удовлетворяет ли она некоторым критериям. Или его даже можно изготовить в реальном мире с помощью такого метода, как 3D-печать или лазерная резка.

Дискретное представление формы

Как и любая другая форма, формы, используемые при обработке геометрии, имеют свойства, относящиеся к их геометрии и топологии . Геометрия фигуры касается положения точек фигуры в пространстве , касательных , нормалей и кривизны . Сюда также входит измерение, в котором находится фигура (например, или ). Топология фигуры — это набор свойств, которые не изменяются даже после применения к фигуре плавных преобразований . Это касается таких размеров, как количество отверстий и границ , а также ориентируемости формы. Одним из примеров неориентируемой формы является лента Мёбиуса . ${\displaystyle R^{2}}$ ${\displaystyle R^{3}}$

В компьютерах все должно быть дискретизировано. Формы при обработке геометрии обычно представляются в виде треугольных сеток , которые можно рассматривать как график . Каждый узел графа представляет собой вершину (обычно в ), у которой есть позиция. Это кодирует геометрию формы. Направленные ребра соединяют эти вершины в треугольники, которые по правилу правой руки имеют направление, называемое нормалью. Каждый треугольник образует грань сетки. Они носят комбинаторный характер и кодируют топологию фигуры. Помимо треугольников, для представления фигуры также можно использовать более общий класс полигональных сеток . Более сложные представления, такие как прогрессивные сетки, кодируют грубое представление вместе с последовательностью преобразований, которые создают точное представление формы или формы с высоким разрешением после ее применения. Эти сетки полезны в различных приложениях, включая геоморфизацию, прогрессивную передачу, сжатие сетки и выборочное уточнение. ^[2] ${\displaystyle R^{3}}$

Сетка знаменитого Стэнфордского кролика. Фигуры обычно представляются в виде сетки — набора многоугольников, очерчивающих контуры фигуры.

Свойства фигуры

Эйлерова характеристика

Одним из особенно важных свойств трехмерной формы является ее эйлерова характеристика , которую альтернативно можно определить через ее род . Формула для этого в непрерывном смысле: , где – количество связных компонентов, – количество отверстий (как в бублике, см. тор ), – количество связных компонентов границы поверхности. Конкретным примером этого является сетка пары брюк . Имеется один связный компонент, 0 отверстий и 3 связных компонента границы (талия и два отверстия для ног). Итак, в этом случае эйлерова характеристика равна -1. Чтобы перенести это в дискретный мир, эйлерова характеристика сетки вычисляется в терминах ее вершин, ребер и граней. . ${\displaystyle \chi =2c-2h-b}$ ${\displaystyle c}$ ${\displaystyle h}$ ${\displaystyle b}$ ${\displaystyle \chi =|V|-|E|+|F|}$

На этом изображении показана сетка пары брюк с эйлеровой характеристикой -1. Это объясняется уравнением для расчета характеристики: 2c – 2h – b. Сетка имеет 1 связный компонент, 0 топологических отверстий и 3 границы (отверстие в талии и каждое отверстие для ног): 2 – 0 – 3 = -1.

Реконструкция поверхности

Реконструкция Пуассона от точек поверхности до сетки

Треугольная сетка строится из облака точек . Иногда фигуры инициализируются только как «облака точек» — набор точек, выбранных с поверхности фигуры. Часто эти облака точек необходимо преобразовать в сетки.

В зависимости от того, как форма инициализируется или «рождается», форма может существовать только как туманность из выбранных точек, которые представляют ее поверхность в пространстве. Чтобы преобразовать точки поверхности в сетку, можно использовать стратегию реконструкции Пуассона ^{[3] .} Этот метод утверждает, что индикаторная функция — функция, которая определяет, какие точки в пространстве принадлежат поверхности фигуры, — на самом деле может быть вычислена на основе точек выборки. Ключевая идея заключается в том, что градиент индикаторной функции равен 0 везде, кроме точек выборки, где он равен внутренней нормали к поверхности. Более формально, предположим, что набор выбранных точек с поверхности обозначается , каждая точка в пространстве - , а соответствующая нормаль в этой точке - . Тогда градиент индикаторной функции определяется как: ${\displaystyle S}$ ${\displaystyle p_{i}}$ ${\displaystyle n_{i}}$

${\displaystyle \triangledown g={\begin{cases}{\textbf {n}}_{i},&\forall p_{i}\in S\\0,&{\text{otherwise}}\end{cases}}}$

Тогда задача реконструкции становится вариационной задачей. Чтобы найти индикаторную функцию поверхности, необходимо найти такую ​​минимизируемую функцию, где – векторное поле, определяемое образцами. В качестве вариационной задачи можно рассматривать минимизатор как решение уравнения Пуассона . ^[3] После получения хорошего приближения и значения , при котором точки с лежат на восстанавливаемой поверхности, алгоритм марширующих кубов можно использовать для построения треугольной сетки из функции , которую затем можно применять в последующей компьютерной графике Приложения. ${\displaystyle \chi }$ ${\displaystyle \lVert \triangledown \chi -{\textbf {V}}\rVert }$ ${\displaystyle {\textbf {V}}}$ ${\displaystyle \chi }$ ${\displaystyle \chi }$ ${\displaystyle \sigma }$ ${\displaystyle (x,y,z)}$ ${\displaystyle \chi (x,y,z)=\sigma }$ ${\displaystyle \chi }$

Постановка на учет

Одна из распространенных проблем, возникающих при обработке геометрии, заключается в том, как объединить несколько изображений одного объекта, снятых под разными углами или положениями. Эта проблема известна как регистрация . При регистрации мы хотим найти оптимальное жесткое преобразование , которое выровняет поверхность с поверхностью . Более формально, если — проекция точки x с поверхности на поверхность , мы хотим найти оптимальную матрицу вращения и вектор перемещения , которые минимизируют следующую целевую функцию: ${\displaystyle X}$ ${\displaystyle Y}$ ${\displaystyle P_{Y}(x)}$ ${\displaystyle X}$ ${\displaystyle Y}$ ${\displaystyle R}$ ${\displaystyle t}$

${\displaystyle \int _{x\in X}||Rx+t-P_{Y}(x)||^{2}dx}$

Хотя вращения в целом нелинейны, небольшие вращения можно линеаризовать как кососимметричные матрицы. Более того, функция расстояния нелинейна, но поддается линейным аппроксимациям, если изменение невелико. Поэтому итеративное решение, такое как итеративная ближайшая точка (ICP), используется для итеративного решения небольших преобразований вместо решения потенциально большого преобразования за один раз. В ICP выбираются n случайных точек выборки и проецируются на . Чтобы равномерно и случайным образом отбирать точки по поверхности треугольной сетки, случайная выборка разбивается на два этапа: равномерная выборка точек внутри треугольника; и треугольники с неравномерной выборкой, так что соответствующая вероятность каждого треугольника пропорциональна площади его поверхности. ^[4] После этого оптимальное преобразование рассчитывается на основе разницы между каждым из них и его проекцией. На следующей итерации прогнозы рассчитываются на основе результата применения предыдущего преобразования к выборкам. Процесс повторяется до сходимости. ${\displaystyle x-P_{Y}(x)}$ ${\displaystyle X}$ ${\displaystyle X}$ ${\displaystyle Y}$ ${\displaystyle x}$

Сглаживание

Когда формы определяются или сканируются, может присутствовать сопутствующий шум либо из-за сигнала, действующего на поверхность, либо из-за фактической геометрии поверхности. Уменьшение шума в первом случае называется шумоподавлением данных , тогда как снижение шума во втором известно как выравнивание поверхности . Задача геометрического сглаживания аналогична уменьшению шума сигнала и, следовательно, использует аналогичные подходы.

Соответствующий лагранжиан, который необходимо минимизировать, получается путем записи соответствия исходному сигналу и гладкости результирующего сигнала, который аппроксимируется величиной градиента с весом : ${\displaystyle {\bar {f}}}$ ${\displaystyle \lambda }$

${\displaystyle {\mathcal {L}}(f)=\int _{\Omega }\|f-{\bar {f}}\|^{2}+\lambda \|\nabla f\|^{2}dx}$.

Взятие вариации выдает необходимое условие ${\displaystyle \delta f}$ ${\displaystyle {\mathcal {L}}}$

${\displaystyle 0=\delta {\mathcal {L}}(f)=\int _{\Omega }\delta f(\mathbf {I} +\lambda \nabla ^{2})f-\delta f{\bar {f}}dx}$.

Дискретизируя это на кусочно-постоянные элементы с нашим сигналом в вершинах, мы получаем

${\displaystyle {\begin{aligned}\sum _{i}M_{i}\delta f_{i}{\bar {f}}_{i}&=\sum _{i}M_{i}\delta f_{i}\sum _{j}(\mathbf {I} +\lambda \nabla ^{2})f_{j}=\sum _{i}\delta f_{i}\sum _{j}(M+\lambda M\nabla ^{2})f_{j},\end{aligned}}}$

Шумная сфера, итеративно сглаживаемая.

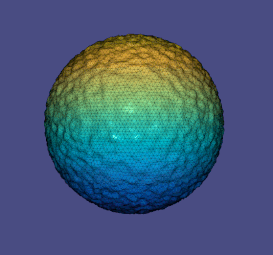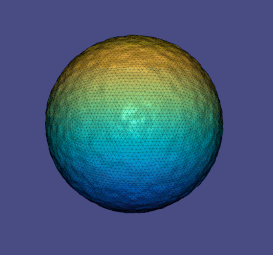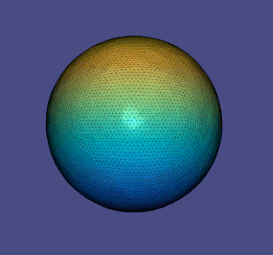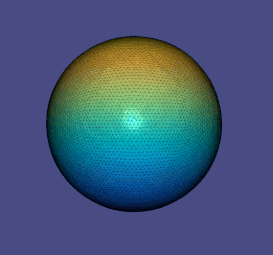
где наш выбор выбран для котангенса Лапласа , а этот термин предназначен для отображения изображения лапласиана из областей в точки. Поскольку изменение является свободным, это приводит к самосопряженной линейной задаче, которую нужно решить с параметром : При работе с треугольными сетками один из способов определения значений матрицы Лапласа — анализ геометрии связанных треугольников на сетке. ${\displaystyle \nabla ^{2}}$ ${\displaystyle M^{-1}\mathbf {L} }$ ${\displaystyle \mathbf {L} }$ ${\displaystyle M^{-1}}$ ${\displaystyle \lambda }$ ${\displaystyle {\bar {f}}=(M+\lambda \mathbf {L} )f.}$ ${\displaystyle L}$

${\displaystyle L_{ij}={\begin{cases}{\frac {1}{2}}(\cot(\alpha _{ij})+\cot(\beta _{ij}))&{\text{edge ij exists}}\\-\sum \limits _{i\neq j}L_{ij}&i=j\\0&{\text{otherwise}}\end{cases}}}$

Где и являются углами, противоположными краю ^[5] Матрица масс M как оператор вычисляет локальный интеграл значения функции и часто устанавливается для сетки с m треугольниками следующим образом: ${\displaystyle \alpha _{ij}}$ ${\displaystyle \beta _{ij}}$ ${\displaystyle (i,j)}$

${\displaystyle M_{ij}={\begin{cases}{\frac {1}{3}}\sum \limits _{t=1}^{m}{\begin{cases}Area(t)&{\text{if triangle t contains vertex i}}\\0&{\text{otherwise}}\end{cases}}&{\text{if i=j}}\\0&{\text{otherwise}}\end{cases}}}$

Параметризация

Иногда нам нужно выровнять 3D-поверхность на плоскую плоскость. Этот процесс известен как параметризация . Цель состоит в том, чтобы найти координаты u и v , на которые мы можем отобразить поверхность, чтобы свести к минимуму искажения. Таким образом, параметризацию можно рассматривать как проблему оптимизации. Одним из основных применений параметризации сетки является наложение текстур .

Метод массовых пружин

Tutte Embedding показывает негладкую параметризацию на стороне жука.

Один из способов измерить искажения, возникающие в процессе картографирования, — это измерить, насколько длина ребер 2D-картографии отличается от их длин на исходной 3D-поверхности. Более формально целевую функцию можно записать так:

${\displaystyle {\underset {U}{\text{min}}}\sum _{ij\in E}||u_{i}-u_{j}||^{2}}$

Где — набор ребер сетки и — набор вершин. Однако оптимизация этой целевой функции приведет к решению, которое сопоставит все вершины с одной вершиной в координатах uv . Заимствуя идею из теории графов, мы применяем Tutte Mapping и ограничиваем граничные вершины сетки единичным кругом или другим выпуклым многоугольником . Это предотвратит схлопывание вершин в одну вершину при применении сопоставления. Неграничные вершины затем размещаются в барицентрической интерполяции своих соседей. Однако Tutte Mapping по-прежнему страдает от серьезных искажений, поскольку пытается сделать длины ребер равными и, следовательно, неправильно учитывает размеры треугольников на фактической поверхностной сетке. ${\displaystyle E}$ ${\displaystyle U}$

Конформные отображения метода наименьших квадратов

Сравнение параметризации Tutte Embedding и Least-Squares-Conformal-Mapping. Обратите внимание, насколько плавна параметризация LSCM на стороне жука.

Другой способ измерения искажения — рассмотреть изменения координатных функций u и v . Шатание и искажение, наблюдаемые в методах массовых пружин, обусловлены сильными изменениями координатных функций u и v . При таком подходе целевой функцией становится энергия Дирихле на u и v:

${\displaystyle {\underset {u,v}{\text{min}}}\int _{S}||\nabla u||^{2}+||\nabla v||^{2}dA}$

Есть еще несколько вещей, которые следует учитывать. Мы хотели бы минимизировать угловое искажение, чтобы сохранить ортогональность . Это значит, что нам бы хотелось . Кроме того, нам также хотелось бы, чтобы отображение имело регионы пропорционально такого же размера, что и оригинал. Это приводит к установке якобиана координатных функций u и v равным 1. ${\displaystyle \nabla u=\nabla v^{\perp }}$

${\displaystyle {\begin{bmatrix}{\dfrac {\partial u}{\partial x}}&{\dfrac {\partial u}{\partial y}}\\[1em]{\dfrac {\partial v}{\partial x}}&{\dfrac {\partial v}{\partial y}}\end{bmatrix}}=1}$

Объединив эти требования, мы можем увеличить энергию Дирихле так, чтобы наша целевая функция стала следующей: ^{[6] [7]}

${\displaystyle {\underset {u,v}{\text{min}}}\int _{S}{\frac {1}{2}}||\nabla u||^{2}+{\frac {1}{2}}||\nabla v||^{2}-\nabla u\cdot \nabla v^{\perp }}$

Чтобы избежать проблемы отображения всех вершин в одну точку, мы также требуем, чтобы решение задачи оптимизации имело ненулевую норму и было ортогонально тривиальному решению.

Деформация

Пример максимально жесткой деформации.

Деформация связана с преобразованием некоторой формы покоя в новую форму. Обычно эти преобразования непрерывны и не меняют топологию фигуры. Современные методы деформации формы на основе сетки удовлетворяют ограничениям пользователя на деформацию в маркерах (выбранных вершинах или областях сетки) и плавно распространяют эти деформации маркеров на остальную часть формы, не удаляя и не искажая детали. Некоторые распространенные формы интерактивных деформаций основаны на точках, скелетах и ​​клетках. ^[8] При точечной деформации пользователь может применять преобразования к небольшому набору точек, называемых маркерами формы. Деформация на основе скелета определяет скелет формы, который позволяет пользователю перемещать кости и вращать суставы. Деформация на основе клетки требует, чтобы клетка была нарисована вокруг всей фигуры или ее части, чтобы, когда пользователь манипулирует точками на клетке, объем, который она включает, изменяется соответствующим образом.

Точечная деформация

Ручки обеспечивают редкий набор ограничений для деформации: когда пользователь перемещает одну точку, остальные должны оставаться на месте.

Поверхность покоя , погруженную в, можно описать отображением , где – двумерная параметрическая область. То же самое можно сделать и с другим отображением преобразованной поверхности . В идеале преобразованная форма добавляет к оригиналу как можно меньше искажений. Один из способов смоделировать это искажение — использовать смещения с энергией, основанной на лапласиане. ^[9] Применение оператора Лапласа к этим отображениям позволяет нам измерить, как изменяется положение точки относительно ее окрестности, что сохраняет ручки гладкими. Таким образом, энергию, которую мы хотели бы минимизировать, можно записать как: ${\displaystyle {\hat {S}}}$ ${\displaystyle \mathbb {R} ^{3}}$ ${\displaystyle {\hat {x}}:\Omega \rightarrow \mathbb {R} ^{3}}$ ${\displaystyle \Omega }$ ${\displaystyle x}$ ${\displaystyle S}$ ${\displaystyle d=x-{\hat {x}}}$

${\displaystyle \min _{\textbf {d}}\int _{\Omega }||\Delta {\textbf {d}}||^{2}dA}$.

Хотя этот метод является трансляционно-инвариантным, он не может учитывать вращения. Схема деформации «как можно жестче» ^[10] применяет жесткое преобразование к каждой ручке i, где – матрица вращения, а – вектор перемещения. К сожалению, заранее узнать повороты невозможно, поэтому вместо этого мы выбираем «лучшее» вращение, которое минимизирует смещения. Однако для достижения локальной инвариантности вращения требуется функция , которая выводит наилучшее вращение для каждой точки на поверхности. Таким образом, результирующая энергия должна быть оптимизирована по обоим параметрам : ${\displaystyle x_{i}=R{\hat {x_{i}}}+t}$ ${\displaystyle R\in SO(3)\subset \mathbb {R} ^{3}}$ ${\displaystyle t\in \mathbb {R} ^{3}}$ ${\displaystyle {\textbf {R}}:\Omega \rightarrow SO(3)}$ ${\displaystyle {\textbf {x}}}$ ${\displaystyle {\textbf {R}}}$

${\displaystyle \min _{{\textbf {x,R}}\in SO(3)}\int _{\Omega }||\nabla {\textbf {x}}-{\textbf {R}}\nabla {\hat {\textbf {x}}}||^{2}dA}$

Обратите внимание, что вектор перевода не присутствует в конечной целевой функции, поскольку переводы имеют постоянный градиент.

Сегментация внутри и снаружи

Хотя это и кажется тривиальным, во многих случаях определение внутренней и внешней сторон треугольной сетки является непростой задачей. В общем, учитывая поверхность, мы ставим эту задачу как определение функции , которая будет возвращать значение, если точка находится внутри , и в противном случае. ${\displaystyle S}$ ${\displaystyle isInside(q)}$ ${\displaystyle 1}$ ${\displaystyle q}$ ${\displaystyle S}$ ${\displaystyle 0}$

В простейшем случае форма замкнутая. В этом случае, чтобы определить, находится ли точка внутри или снаружи поверхности, мы можем направить луч в любом направлении от точки запроса и подсчитать, сколько раз он пройдет через поверхность. Если он находился снаружи , то луч должен либо не пройти (в этом случае ), либо каждый раз, когда он входит, он должен пройти дважды, поскольку S ограничено, поэтому любой луч, входящий в него, должен выйти. Так что если снаружи, то четно. Аналогично, если находится внутри, та же логика применима и к предыдущему случаю, но луч должен пересечь еще один раз при первом выходе из него . Так: ${\displaystyle q}$ ${\displaystyle r}$ ${\displaystyle count_{r}}$ ${\displaystyle q}$ ${\displaystyle S}$ ${\displaystyle S}$ ${\displaystyle count_{r}=0}$ ${\displaystyle S}$ ${\displaystyle q}$ ${\displaystyle count_{r}}$ ${\displaystyle q}$ ${\displaystyle S}$ ${\displaystyle S}$

${\displaystyle isInside_{r}(q)=\left\{{\begin{array}{ll}1&count_{r}\ is\ odd\\0&count_{r}\ is\ even\\\end{array}}\right.}$

Зачастую мы не можем гарантировать, что сайт закрыт. Возьмите пример с брюками из начала этой статьи. Эта сетка явно имеет смысловое содержание внутри и снаружи, несмотря на наличие дырок на талии и ногах. ${\displaystyle S}$

Аппроксимация сегментации внутри и снаружи путем стрельбы лучами из точки запроса для различного количества лучей.

Наивная попытка решить эту проблему состоит в том, чтобы пустить множество лучей в случайных направлениях и классифицировать их как находящиеся внутри тогда и только тогда, когда большинство лучей пересекались нечетное число раз. Чтобы выразить это количественно, скажем, мы излучаем лучи . Мы связываем число , которое представляет собой среднее значение каждого луча. Поэтому: ${\displaystyle q}$ ${\displaystyle S}$ ${\displaystyle k}$ ${\displaystyle r_{1},r_{2},\dots ,r_{k}}$ ${\displaystyle rayTest(q)={\frac {1}{k}}\sum _{i=1}^{k}isInside_{r_{i}}(q)}$ ${\displaystyle isInside_{r}}$

${\displaystyle isInside(q)=\left\{{\begin{array}{ll}1&rayTest(q)\geq 0.5\\0&rayTest(q)<0.5\\\end{array}}\right.}$

В пределе съемки большого количества лучей этот метод обрабатывает открытые сетки, однако для достижения точности требуется слишком много лучей, чтобы этот метод был идеальным в вычислительном отношении. Вместо этого более надежным подходом является обобщенное число обмотки. ^[11] Вдохновленный двумерным числом витков , этот подход использует телесный угол каждого треугольника в сетке, чтобы определить, находится ли он внутри или снаружи. Значение Обобщенного числа обмотки при , пропорционально сумме вклада телесного угла от каждого треугольника в сетке: ${\displaystyle q}$ ${\displaystyle q}$ ${\displaystyle q}$ ${\displaystyle wn(q)}$

${\displaystyle wn(q)={\frac {1}{4\pi }}\sum _{t\in F}solidAngle(t)}$

Для замкнутой сетки эквивалентно характеристической функции объема, представленной . Поэтому мы говорим: ${\displaystyle wn(q)}$ ${\displaystyle S}$

${\displaystyle isInside(q)=\left\{{\begin{array}{ll}1&wn(q)\geq 0.5\\0&wn(q)<0.5\\\end{array}}\right.}$

Поскольку это гармоническая функция , она плавно деградирует, а это означает, что сегментация внутри и снаружи не сильно изменится, если мы проделаем дыры в замкнутой сетке. По этой причине Обобщенное Число Обмоток надежно обрабатывает открытые сетки. Граница между внутренним и внешним плавно проходит через отверстия в сетке. Фактически, в пределе Обобщенное Число Обмоток эквивалентно методу распределения лучей, поскольку количество лучей стремится к бесконечности. ${\displaystyle wn(q)}$

Приложения

• Компьютерное проектирование (САПР)
• 3D-реконструкция поверхности, например , сканеры дальности в службах безопасности аэропортов, автономные транспортные средства, реконструкция данных медицинских сканеров.
• Регистрация изображения в мире, например, хирургия под контролем изображения
• Архитектура , например создание, реверс-инжиниринг
• Физическое моделирование
• Компьютерные игры, например, обнаружение столкновений
• Геологическое моделирование
• Визуализация (графика), например, информационная визуализация , математическая визуализация.
• Наложение текстур
• Моделирование биологических систем, например. моделирование мышц и костей, отслеживание рук в реальном времени

Смотрите также

• Вариационное исчисление
• Компьютерная графика
  • 3D компьютерная графика
  • Графический процессор (GPU)
• Компьютерное проектирование (САПР)
• Цифровое изображение
  • Цифровая обработка изображений
• Дискретная дифференциальная геометрия
• Глоссарий дифференциальной геометрии и топологии
• Промышленное компьютерное сканирование
• Список программного обеспечения для интерактивной геометрии
• МешЛаб
• Обработка сигнала
  • Цифровая обработка сигналов
  • Цифровой сигнальный процессор (DSP)
• Топология

Рекомендации

1. Ботч, Марио; Коббельт, Лейф; Поли, Марк; Альье, Пьер (2010). Обработка полигональной сетки . ЦРК Пресс . ISBN 9781568814261.
2. Хьюг Хоппе. «Прогрессивные сетки» (PDF) .
3. «Реконструкция поверхности Пуассона». hhoppe.com . Проверено 26 января 2017 г.
4. Шимон Русинкевич, Марк Левой. «Эффективные варианты алгоритма ICP» (PDF) .
5. "Крис Трэли: Лапласовы сетки". www.ctralie.com . Проверено 16 марта 2017 г.
6. Дебрен, Матье (2002). «Внутренняя параметризация поверхностных сеток» (PDF) . Еврографика . 21 .
7. Леви, Бруно (2002). «Конформные карты наименьших квадратов для автоматического создания атласов текстур» (PDF) . Транзакции ACM с графикой . 21 (3): 362–371. дои : 10.1145/566654.566590.
8. Джейкобсон, Алек; Баран, Илья; Попович, Йован; Соркин, Ольга (2011). «Ограниченные бигармонические веса для деформации в реальном времени» (PDF) . Транзакции ACM с графикой . 30 (4): 1. дои : 10.1145/2010324.1964973.
9. Марк, Алекса (2003). «Дифференциальные координаты для локального морфинга и деформации сетки». Визуальный компьютер . 19 (2): 105–114. дои : 10.1007/s00371-002-0180-0. S2CID  6847571.
10. Соркин, Ольга ; Алекса, Марк (2007). «Моделирование максимально жесткой поверхности» (PDF) . Материалы симпозиума EUROGRAPHICS/ACM SIGGRAPH по геометрической обработке : 109–116.
11. Джейкобсон, Алек; Ладислав, Каван; Соркин-Хорнунг, Ольга (2013). «Надежная сегментация внутри и снаружи с использованием обобщенных чисел обмотки» (PDF) . Транзакции ACM с графикой . 32 (4): 1. дои : 10.1145/2461912.2461916. S2CID  207202533.

Внешние ссылки

• Симпозиум по геометрической обработке
• Группа мультирезерного моделирования, Калифорнийский технологический институт
• Группа обработки математической геометрии, Свободный университет Берлина
• Группа компьютерной графики, RWTH Ахенского университета
• Книга по обработке полигональной сетки
• Библиотека обработки полигональной сетки
• Дискретная дифференциальная геометрия: прикладное введение, конспекты курса Кинана Крейна и др.
• Видеоуроки от аспирантуры ПМГ 2017
• библиотека обработки геометрии libigl
• CGAL Библиотека алгоритмов вычислительной геометрии (см. раздел «Обработка полигональной сетки»)