Кодирование Хаффмана

Метод сжатия данных

Дерево Хаффмана, сгенерированное из точных частот текста "это пример дерева Хаффмана". Кодирование предложения этим кодом требует 135 (или 147) бит, в отличие от 288 (или 180) бит, если бы использовались 36 символов по 8 (или 5) бит (предполагается, что структура кодового дерева известна декодеру и, таким образом, не должна учитываться как часть передаваемой информации). Частоты и коды каждого символа показаны в прилагаемой таблице.

В информатике и теории информации код Хаффмана — это особый тип оптимального префиксного кода , который обычно используется для сжатия данных без потерь . Процесс нахождения или использования такого кода — это кодирование Хаффмана , алгоритм, разработанный Дэвидом А. Хаффманом , когда он был студентом -докторантурой Массачусетского технологического института , и опубликованный в статье 1952 года «Метод построения кодов с минимальной избыточностью». ^[1]

Выходные данные алгоритма Хаффмана можно рассматривать как таблицу кодов переменной длины для кодирования исходного символа (например, символа в файле). Алгоритм выводит эту таблицу из оценочной вероятности или частоты появления ( веса ) для каждого возможного значения исходного символа. Как и в других методах энтропийного кодирования , более распространенные символы обычно представляются с использованием меньшего количества бит, чем менее распространенные символы. Метод Хаффмана может быть эффективно реализован, находя код за время, линейное количеству входных весов, если эти веса отсортированы. ^[2] Однако, хотя кодирование Хаффмана является оптимальным среди методов, кодирующих символы по отдельности, оно не всегда оптимально среди всех методов сжатия — его заменяют арифметическим кодированием ^[3] или асимметричными системами счисления ^[4], если требуется лучшая степень сжатия.

История

В 1951 году Дэвиду А. Хаффману и его однокурсникам по теории информации в Массачусетском технологическом институте был предоставлен выбор между курсовой работой и выпускным экзаменом . Профессор Роберт М. Фано задал курсовую работу по проблеме поиска наиболее эффективного двоичного кода. Хаффман, неспособный доказать, что какие-либо коды являются наиболее эффективными, собирался сдаться и начать готовиться к выпускному, когда ему пришла в голову идея использовать частотно-отсортированное двоичное дерево , и быстро доказал, что этот метод наиболее эффективен. ^[5]

При этом Хаффман превзошел Фано, который работал с Клодом Шенноном над разработкой похожего кода. Построение дерева снизу вверх гарантировало оптимальность, в отличие от подхода сверху вниз кодирования Шеннона–Фано .

Терминология

Кодирование Хаффмана использует определенный метод выбора представления для каждого символа, что приводит к префиксному коду (иногда называемому «кодами без префиксов», то есть битовая строка, представляющая некоторый конкретный символ, никогда не является префиксом битовой строки, представляющей любой другой символ). Кодирование Хаффмана является настолько распространенным методом создания префиксных кодов, что термин «код Хаффмана» широко используется как синоним «префиксного кода», даже если такой код не создается алгоритмом Хаффмана.

Определение проблемы

Построение дерева Хаффмана

Неформальное описание

Данный

Набор символов и их весов (обычно пропорциональных вероятностям).

Находить

Двоичный код без префиксов (набор кодовых слов) с минимальной ожидаемой длиной кодового слова (эквивалентно дереву с минимальной взвешенной длиной пути от корня).

Формализованное описание

Входные данные .
Алфавит , который является алфавитом символов размера . Кортеж , который является кортежем (положительных) весов символов (обычно пропорциональных вероятностям), т. е . Выходные данные . Код , который является кортежем (двоичных) кодовых слов, где — кодовое слово для . Цель . Пусть будет взвешенной длиной пути кода . Условие: для любого кода . ${\displaystyle A=(a_{1},a_{2},\dots ,a_{n})}$ ${\displaystyle n}$
${\displaystyle W=(w_{1},w_{2},\dots ,w_{n})}$ ${\displaystyle w_{i}=\operatorname {weight} \left(a_{i}\right),\,i\in \{1,2,\dots ,n\}}$


${\displaystyle C\left(W\right)=(c_{1},c_{2},\dots ,c_{n})}$ ${\displaystyle c_{i}}$ ${\displaystyle a_{i},\,i\in \{1,2,\dots ,n\}}$


${\textstyle L\left(C\left(W\right)\right)=\sum _{i=1}^{n}{w_{i}\operatorname {length} \left(c_{i}\right)}}$ ${\displaystyle C}$ ${\displaystyle L\left(C\left(W\right)\right)\leq L\left(T\left(W\right)\right)}$ ${\displaystyle T\left(W\right)}$

Пример

Приведем пример результата кодирования Хаффмана для кода с пятью символами и заданными весами. Мы не будем проверять, что он минимизирует L по всем кодам, но вычислим L и сравним его с энтропией Шеннона H заданного набора весов; результат близок к оптимальному.

Для любого кода, который является двузначным , что означает, что код однозначно декодируется , сумма вероятностных бюджетов по всем символам всегда меньше или равна единице. В этом примере сумма строго равна единице; в результате код называется полным кодом. Если это не так, всегда можно получить эквивалентный код, добавив дополнительные символы (с соответствующими нулевыми вероятностями), чтобы сделать код полным, сохранив при этом двузначность .

Согласно определению Шеннона (1948) , информационное содержание h (в битах) каждого символа a _i с ненулевой вероятностью равно

${\displaystyle h(a_{i})=\log _{2}{1 \over w_{i}}.}$

Энтропия H (в битах ) представляет собой взвешенную сумму по всем символам a _i с ненулевой вероятностью w _i информационного содержания каждого символа:

$${\displaystyle H(A)=\sum _{w_{i}>0}w_{i}h(a_{i})=\sum _{w_{i}>0}w_{i}\log _{2}{1 \over w_{i}}=-\sum _{w_{i}>0}w_{i}\log _{2}{w_{i}}.}$$

(Примечание: символ с нулевой вероятностью имеет нулевой вклад в энтропию, поскольку . Поэтому для простоты символы с нулевой вероятностью можно исключить из формулы выше.) ${\displaystyle \lim _{w\to 0^{+}}w\log _{2}w=0}$

Как следствие теоремы Шеннона о кодировании источника , энтропия является мерой наименьшей длины кодового слова, которая теоретически возможна для данного алфавита с соответствующими весами. В этом примере средневзвешенная длина кодового слова составляет 2,25 бита на символ, что лишь немного больше расчетной энтропии 2,205 бита на символ. Таким образом, этот код не только оптимален в том смысле, что никакой другой возможный код не работает лучше, но и очень близок к теоретическому пределу, установленному Шенноном.

В общем случае код Хаффмана не обязательно должен быть уникальным. Таким образом, набор кодов Хаффмана для заданного распределения вероятностей является непустым подмножеством кодов, минимизирующих это распределение вероятностей. (Однако для каждого назначения минимизирующей длины кодового слова существует по крайней мере один код Хаффмана с этими длинами.) ${\displaystyle L(C)}$

Базовая техника

Сжатие

Визуализация использования кодирования Хаффмана для кодирования сообщения "A_DEAD_DAD_CEDED_A_BAD_BABE_A_BEADED_ABACA_
BED". На шагах 2–6 буквы сортируются по возрастанию частоты, а наименее частые две на каждом шаге объединяются и повторно вставляются в список, и строится частичное дерево. Последнее дерево на шаге 6 просматривается для генерации словаря на шаге 7. Шаг 8 использует его для кодирования сообщения.

Источник генерирует 4 различных символа с вероятностью . Двоичное дерево генерируется слева направо, беря два наименее вероятных символа и объединяя их для формирования другого эквивалентного символа, имеющего вероятность, равную сумме двух символов. Процесс повторяется до тех пор, пока не останется только один символ. Затем дерево можно прочитать в обратном направлении, справа налево, назначая разные биты разным ветвям. Окончательный код Хаффмана: ${\displaystyle \{a_{1},a_{2},a_{3},a_{4}\}}$ ${\displaystyle \{0.4;0.35;0.2;0.05\}}$Стандартный способ представления сигнала, состоящего из 4 символов, заключается в использовании 2 бит/символ, но энтропия источника составляет 1,74 бит/символ. Если этот код Хаффмана используется для представления сигнала, то средняя длина снижается до 1,85 бит/символ; это все еще далеко от теоретического предела, поскольку вероятности символов отличаются от отрицательных степеней двойки.

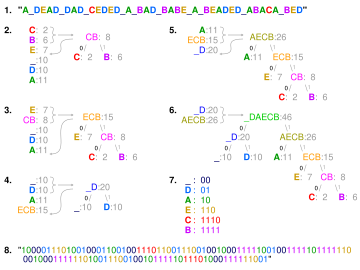
Метод работает путем создания бинарного дерева узлов. Они могут храниться в обычном массиве , размер которого зависит от количества символов, . Узел может быть либо листовым узлом , либо внутренним узлом . Изначально все узлы являются листовыми узлами, которые содержат сам символ , вес (частоту появления) символа и, по желанию, ссылку на родительский узел, что позволяет легко читать код (в обратном порядке), начиная с листового узла. Внутренние узлы содержат вес , ссылки на два дочерних узла и необязательную ссылку на родительский узел. Как правило, бит «0» представляет собой следование за левым дочерним элементом, а бит «1» представляет собой следование за правым дочерним элементом. Готовое дерево имеет до листовых узлов и внутренних узлов. Дерево Хаффмана, в котором опущены неиспользуемые символы, создает наиболее оптимальную длину кода. ${\displaystyle n}$ ${\displaystyle n}$ ${\displaystyle n-1}$

Процесс начинается с конечных узлов, содержащих вероятности символа, который они представляют. Затем процесс берет два узла с наименьшей вероятностью и создает новый внутренний узел, имеющий эти два узла в качестве дочерних. Вес нового узла устанавливается равным сумме весов дочерних узлов. Затем мы снова применяем процесс к новому внутреннему узлу и к оставшимся узлам (т. е. исключаем два конечных узла), мы повторяем этот процесс, пока не останется только один узел, который является корнем дерева Хаффмана.

Простейший алгоритм построения использует приоритетную очередь , где узлу с наименьшей вероятностью присваивается наивысший приоритет:

1. Создайте конечный узел для каждого символа и добавьте его в приоритетную очередь.
2. Пока в очереди находится более одного узла:
   1. Удалить из очереди два узла с наивысшим приоритетом (наименьшая вероятность)
   2. Создайте новый внутренний узел с этими двумя узлами в качестве дочерних и с вероятностью, равной сумме вероятностей двух узлов.
   3. Добавьте новый узел в очередь.
3. Оставшийся узел является корневым узлом, и дерево завершено.

Поскольку эффективные структуры данных очереди с приоритетами требуют O(log n ) времени на вставку, а дерево с n листьями имеет 2 n −1 узлов, этот алгоритм работает за время O( n log n ), где n — количество символов.

Если символы сортируются по вероятности, существует метод линейного времени (O( n )) для создания дерева Хаффмана с использованием двух очередей , первая из которых содержит начальные веса (вместе с указателями на связанные листья), а объединенные веса (вместе с указателями на деревья) помещаются в конец второй очереди. Это гарантирует, что наименьший вес всегда будет находиться в начале одной из двух очередей:

1. Начните с такого количества листьев, сколько символов.
2. Поместить все конечные узлы в первую очередь (по возрастанию вероятности, так чтобы наименее вероятный элемент оказался в начале очереди).
3. Пока в очередях находится более одного узла:
   1. Исключите из очереди два узла с наименьшим весом, проверив фронты обеих очередей.
   2. Создайте новый внутренний узел с двумя только что удаленными узлами в качестве дочерних (любой узел может быть дочерним), а сумму их весов — в качестве нового веса.
   3. Добавьте новый узел в конец второй очереди.
4. Оставшийся узел является корневым; дерево теперь сформировано.

После генерации дерева Хаффмана оно просматривается для генерации словаря, который сопоставляет символы с двоичными кодами следующим образом:

1. Начните с установки текущего узла в качестве корня.
2. Если узел не является листовым узлом, обозначьте ребро к левому потомку как 0 , а ребро к правому потомку как 1. Повторите процесс как для левого потомка, так и для правого потомка.

Окончательная кодировка любого символа затем считывается путем конкатенации меток на ребрах вдоль пути от корневого узла к символу.

Во многих случаях временная сложность не имеет большого значения при выборе алгоритма, поскольку n здесь — это количество символов в алфавите, которое обычно является очень малым числом (по сравнению с длиной кодируемого сообщения); тогда как анализ сложности касается поведения, когда n становится очень большим.

Обычно полезно минимизировать дисперсию длины кодового слова. Например, буфер связи, принимающий данные, закодированные по Хаффману, может потребовать большего размера для обработки особенно длинных символов, если дерево особенно несбалансированное. Чтобы минимизировать дисперсию, просто разорвите связи между очередями, выбрав элемент в первой очереди. Эта модификация сохранит математическую оптимальность кодирования Хаффмана, одновременно минимизируя дисперсию и минимизируя длину самого длинного кода символа.

Декомпрессия

Вообще говоря, процесс декомпрессии — это просто вопрос перевода потока префиксных кодов в отдельные значения байтов, обычно путем обхода узла за узлом дерева Хаффмана по мере считывания каждого бита из входного потока (достижение листового узла обязательно завершает поиск этого конкретного значения байта). Однако прежде чем это может произойти, дерево Хаффмана должно быть каким-то образом реконструировано. В простейшем случае, когда частоты символов достаточно предсказуемы, дерево может быть предварительно построено (и даже статистически скорректировано на каждом цикле сжатия) и, таким образом, повторно использоваться каждый раз, за ​​счет, по крайней мере, некоторой меры эффективности сжатия. В противном случае информация для реконструкции дерева должна быть отправлена ​​априори. Наивный подход может заключаться в добавлении счетчика частот каждого символа к потоку сжатия. К сожалению, накладные расходы в таком случае могут составить несколько килобайт, поэтому этот метод имеет мало практического применения. Если данные сжимаются с использованием канонического кодирования , модель сжатия может быть точно реконструирована всего лишь с помощью битов информации (где B — количество бит на символ). Другой метод заключается в простом добавлении дерева Хаффмана, бит за битом, к выходному потоку. Например, предположив, что значение 0 представляет родительский узел, а 1 — конечный узел, всякий раз, когда встречается последний, процедура построения дерева просто считывает следующие 8 бит, чтобы определить значение символа этого конкретного листа. Процесс продолжается рекурсивно до тех пор, пока не будет достигнут последний конечный узел; в этот момент дерево Хаффмана будет, таким образом, точно восстановлено. Накладные расходы при использовании такого метода составляют примерно от 2 до 320 байт (предполагая 8-битный алфавит). Возможны и многие другие методы. В любом случае, поскольку сжатые данные могут включать неиспользуемые «конечные биты», декомпрессор должен иметь возможность определять, когда прекратить выдачу выходных данных. Это можно сделать либо путем передачи длины распакованных данных вместе с моделью сжатия, либо путем определения специального символа кода для обозначения конца ввода (последний метод может отрицательно повлиять на оптимальность длины кода, однако). ${\displaystyle B\cdot 2^{B}}$

Основные свойства

Используемые вероятности могут быть общими для области применения, основанными на среднем опыте, или они могут быть фактическими частотами, найденными в сжимаемом тексте. Для этого требуется, чтобы таблица частот хранилась вместе со сжатым текстом. См. раздел «Распаковка» выше для получения дополнительной информации о различных методах, используемых для этой цели.

Оптимальность

Оригинальный алгоритм Хаффмана оптимален для кодирования посимвольно с известным распределением входной вероятности, т. е. отдельного кодирования несвязанных символов в таком потоке данных. Однако он не оптимален, когда ограничение посимвольно опущено или когда функции массы вероятности неизвестны. Кроме того, если символы не являются независимыми и одинаково распределенными , одного кода может быть недостаточно для оптимальности. Другие методы, такие как арифметическое кодирование, часто имеют лучшую способность сжатия.

Хотя оба вышеупомянутых метода могут объединять произвольное количество символов для более эффективного кодирования и в целом адаптироваться к фактической входной статистике, арифметическое кодирование делает это без значительного увеличения вычислительной или алгоритмической сложности (хотя самая простая версия медленнее и сложнее, чем кодирование Хаффмана). Такая гибкость особенно полезна, когда входные вероятности точно не известны или значительно различаются в пределах потока. Однако кодирование Хаффмана обычно быстрее, и арифметическое кодирование исторически было предметом некоторой озабоченности по поводу патентных проблем. Таким образом, многие технологии исторически избегали арифметического кодирования в пользу Хаффмана и других методов префиксного кодирования. По состоянию на середину 2010 года наиболее часто используемые методы для этой альтернативы кодированию Хаффмана перешли в общественное достояние, поскольку истекли сроки действия ранних патентов.

Для набора символов с равномерным распределением вероятностей и числом членов, которое является степенью двойки , кодирование Хаффмана эквивалентно простому двоичному блочному кодированию , например, кодированию ASCII . Это отражает тот факт, что сжатие невозможно с таким вводом, независимо от метода сжатия, т. е. оптимальным решением будет ничего не делать с данными.

Кодирование Хаффмана является оптимальным среди всех методов в любом случае, когда каждый входной символ является известной независимой и одинаково распределенной случайной величиной, имеющей вероятность, которая является диадической . Префиксные коды, и, таким образом, кодирование Хаффмана в частности, имеют тенденцию быть неэффективными на небольших алфавитах, где вероятности часто попадают между этими оптимальными (диадическими) точками. Худший случай для кодирования Хаффмана может иметь место, когда вероятность наиболее вероятного символа намного превышает 2 ⁻¹ = 0,5, делая верхний предел неэффективности неограниченным.

Существует два связанных подхода для обхода этой конкретной неэффективности, при этом все еще используя кодирование Хаффмана. Объединение фиксированного числа символов вместе («блокирование») часто увеличивает (и никогда не уменьшает) сжатие. По мере того, как размер блока приближается к бесконечности, кодирование Хаффмана теоретически приближается к пределу энтропии, т. е. к оптимальному сжатию. ^[6] Однако блокирование произвольно больших групп символов непрактично, поскольку сложность кода Хаффмана линейна по числу возможностей для кодирования, число, которое экспоненциально по размеру блока. Это ограничивает объем блокирования, которое выполняется на практике.

Практической альтернативой, широко используемой, является кодирование длин серий . Этот метод добавляет один шаг вперед к энтропийному кодированию, в частности, подсчет (серий) повторяющихся символов, которые затем кодируются. Для простого случая процессов Бернулли кодирование Голомба является оптимальным среди префиксных кодов для кодирования длины серий, что доказано с помощью методов кодирования Хаффмана. ^[7] Похожий подход используется в факсимильных аппаратах, использующих модифицированное кодирование Хаффмана . Однако кодирование длин серий не так адаптируемо к такому количеству типов входных данных, как другие технологии сжатия.

Вариации

Существует множество вариаций кодирования Хаффмана, ^[8] некоторые из которых используют алгоритм, подобный алгоритму Хаффмана, а другие находят оптимальные префиксные коды (например, накладывая различные ограничения на вывод). Обратите внимание, что в последнем случае метод не обязательно должен быть подобным алгоритму Хаффмана и, на самом деле, даже не обязательно должен быть полиномиальным по времени .

н-арное кодирование Хаффмана

n -арный алгоритм Хаффмана использует алфавит {0, 1,..., n − 1} для кодирования сообщения и построения n -арного дерева. Этот подход рассматривался Хаффманом в его оригинальной статье. Тот же алгоритм применяется для двоичных ( ) кодов, за исключением того, что n наименее вероятных символов берутся вместе, а не только 2 наименее вероятных. Обратите внимание, что для n больше 2 не все наборы исходных слов могут правильно сформировать n -арное дерево для кодирования Хаффмана. В этих случаях необходимо добавить дополнительные 0-вероятностные заполнители. Это связано с тем, что дерево должно образовывать контрактор n к 1; ^{[ необходимо разъяснение ]} для двоичного кодирования это контрактор 2 к 1, и любой размерный набор может образовать такой контрактор. Если количество исходных слов сравнимо с 1 по модулю n −1, то набор исходных слов образует правильное дерево Хаффмана. ${\displaystyle n=2}$

Адаптивное кодирование Хаффмана

Вариация, называемая адаптивным кодированием Хаффмана, включает в себя динамическое вычисление вероятностей на основе последних фактических частот в последовательности исходных символов и изменение структуры дерева кодирования для соответствия обновленным оценкам вероятности. На практике он используется редко, поскольку стоимость обновления дерева делает его медленнее, чем оптимизированное адаптивное арифметическое кодирование , которое более гибкое и имеет лучшее сжатие.

Алгоритм шаблона Хаффмана

Чаще всего веса, используемые в реализациях кодирования Хаффмана, представляют собой числовые вероятности, но алгоритм, приведенный выше, этого не требует; он требует только, чтобы веса образовывали полностью упорядоченный коммутативный моноид , что означает способ упорядочивания весов и их сложения. Шаблонный алгоритм Хаффмана позволяет использовать любой вид весов (стоимости, частоты, пары весов, нечисловые веса) и один из многих методов комбинирования (не только сложение). Такие алгоритмы могут решать другие задачи минимизации, такие как минимизация , проблема, впервые примененная к проектированию схем. ${\displaystyle \max _{i}\left[w_{i}+\mathrm {length} \left(c_{i}\right)\right]}$

Кодирование Хаффмана с ограниченной длиной/кодирование Хаффмана с минимальной дисперсией

Кодирование Хаффмана с ограничением длины — это вариант, где целью по-прежнему является достижение минимальной взвешенной длины пути, но есть дополнительное ограничение, что длина каждого кодового слова должна быть меньше заданной константы. Алгоритм слияния пакетов решает эту проблему с помощью простого жадного подхода, очень похожего на тот, который используется алгоритмом Хаффмана. Его временная сложность составляет , где — максимальная длина кодового слова. Неизвестно ни одного алгоритма, который мог бы решить эту задачу за или время, в отличие от предварительно отсортированных и несортированных обычных задач Хаффмана соответственно. ${\displaystyle O(nL)}$ ${\displaystyle L}$ ${\displaystyle O(n)}$ ${\displaystyle O(n\log n)}$

Кодирование Хаффмана с неравной стоимостью букв

В стандартной задаче кодирования Хаффмана предполагается, что каждый символ в наборе, из которого составлены кодовые слова, имеет одинаковую стоимость передачи: кодовое слово, длина которого составляет N цифр, всегда будет иметь стоимость N , независимо от того, сколько из этих цифр нулей, сколько единиц и т. д. При работе с этим предположением минимизация общей стоимости сообщения и минимизация общего количества цифр — это одно и то же.

Кодирование Хаффмана с неравной стоимостью букв является обобщением без этого предположения: буквы кодирующего алфавита могут иметь неравномерную длину из-за характеристик среды передачи. Примером является кодирующий алфавит кода Морзе , где «тире» отправляется дольше, чем «точка», и, следовательно, стоимость тире во времени передачи выше. Цель по-прежнему состоит в минимизации средневзвешенной длины кодового слова, но этого уже недостаточно, чтобы просто минимизировать количество символов, используемых в сообщении. Неизвестно ни одного алгоритма, который бы решал эту задачу таким же образом или с такой же эффективностью, как обычное кодирование Хаффмана, хотя она была решена Ричардом М. Карпом ^[9], чье решение было улучшено для случая целочисленных затрат Мордехаем Дж. Голином. ^[10]

Оптимальные алфавитно-бинарные деревья (кодирование Ху–Таккера)

В стандартной задаче кодирования Хаффмана предполагается, что любое кодовое слово может соответствовать любому входному символу. В алфавитной версии алфавитный порядок входов и выходов должен быть идентичным. Таким образом, например, нельзя назначить code , а вместо этого следует назначить либо или . Это также известно как проблема Ху–Таккера , в честь TC Hu и Alan Tucker , авторов статьи, представляющей первое решение этой оптимальной двоичной алфавитной проблемы, ^[11] которая имеет некоторое сходство с алгоритмом Хаффмана, но не является вариацией этого алгоритма. Более поздний метод, алгоритм Гарсии–Вакса Адриано Гарсии и Мишель Л. Вакс (1977), использует более простую логику для выполнения тех же сравнений за то же общее время. Эти оптимальные алфавитные двоичные деревья часто используются в качестве двоичных деревьев поиска . ^[12] ${\displaystyle A=\left\{a,b,c\right\}}$ ${\displaystyle H\left(A,C\right)=\left\{00,1,01\right\}}$ ${\displaystyle H\left(A,C\right)=\left\{00,01,1\right\}}$ ${\displaystyle H\left(A,C\right)=\left\{0,10,11\right\}}$ ${\displaystyle O(n\log n)}$

Канонический код Хаффмана

Если веса, соответствующие алфавитно упорядоченным входам, находятся в числовом порядке, код Хаффмана имеет те же длины, что и оптимальный алфавитный код, который можно найти, вычислив эти длины, что делает кодирование Ху–Таккера ненужным. Код, полученный в результате численно (пере)упорядоченного входа, иногда называют каноническим кодом Хаффмана , и он часто используется на практике из-за простоты кодирования/декодирования. Методика нахождения этого кода иногда называется кодированием Хаффмана–Шеннона–Фано , поскольку он оптимален, как кодирование Хаффмана, но алфавитен по весовой вероятности, как кодирование Шеннона–Фано . Код Хаффмана–Шеннона–Фано, соответствующий примеру , — это , который, имея ту же длину кодового слова, что и исходное решение, также является оптимальным. Но в каноническом коде Хаффмана результат равен . ${\displaystyle \{000,001,01,10,11\}}$ ${\displaystyle \{110,111,00,01,10\}}$

Приложения

Арифметическое кодирование и кодирование Хаффмана дают эквивалентные результаты — достижение энтропии — когда каждый символ имеет вероятность вида 1/2 ^k . В других обстоятельствах арифметическое кодирование может предложить лучшее сжатие, чем кодирование Хаффмана, потому что — интуитивно — его «кодовые слова» могут иметь фактически нецелые длины бит, тогда как кодовые слова в префиксных кодах, таких как коды Хаффмана, могут иметь только целое число бит. Следовательно, кодовое слово длины k оптимально соответствует только символу с вероятностью 1/2 ^k , а другие вероятности не представлены оптимально; тогда как длина кодового слова в арифметическом кодировании может быть сделана так, чтобы точно соответствовать истинной вероятности символа. Это различие особенно заметно для небольших размеров алфавита. ^{[ необходима цитата ]}

Тем не менее, префиксные коды остаются широко используемыми из-за своей простоты, высокой скорости и отсутствия патентного покрытия . Они часто используются в качестве «бэк-энда» для других методов сжатия. Deflate ( алгоритм PKZIP ) и мультимедийные кодеки, такие как JPEG и MP3, имеют модель интерфейса и квантизацию, за которой следует использование префиксных кодов; их часто называют «кодами Хаффмана», хотя большинство приложений используют предопределенные коды переменной длины, а не коды, разработанные с использованием алгоритма Хаффмана.

Ссылки

1. Хаффман, Д. (1952). "Метод построения кодов с минимальной избыточностью" (PDF) . Труды IRE . 40 (9): 1098–1101. doi :10.1109/JRPROC.1952.273898.
2. Ван Леувен, Ян (1976). «О построении деревьев Хаффмана» (PDF) . ICALP : 382–410 . Получено 20 февраля 2014 г.
3. Ze-Nian Li; Mark S. Drew; Jiangchuan Liu (2014-04-09). Основы мультимедиа. Springer Science & Business Media. ISBN 978-3-319-05290-8.
4. J. Duda, K. Tahboub, NJ Gadil, EJ Delp, Использование асимметричных систем счисления в качестве точной замены кодирования Хаффмана, Симпозиум по кодированию изображений, 2015.
5. Хаффман, Кен (1991). «Профиль: Дэвид А. Хаффман: Кодирование «аккуратности» единиц и нулей». Scientific American : 54–58.
6. Грибов, Александр (2017-04-10). "Оптимальное сжатие полилинии с сегментами и дугами". arXiv : 1604.07476 [cs.CG].
7. Галлагер, РГ; ван Вурхис, ДК (1975). «Оптимальные исходные коды для геометрически распределенных целочисленных алфавитов». Труды IEEE по теории информации . 21 (2): 228–230. doi :10.1109/TIT.1975.1055357.
8. Абрахамс, Дж. (1997-06-11). "Деревья кода и анализа для кодирования исходного кода без потерь". Написано в Арлингтоне, Вирджиния, США. Труды. Сжатие и сложность последовательностей 1997 (Кат. № 97TB100171) . Отделение математики, компьютерных и информационных наук, Управление военно-морских исследований (ONR). Салерно: IEEE . стр. 145–171. CiteSeerX 10.1.1.589.4726 . doi :10.1109/SEQUEN.1997.666911. ISBN  0-8186-8132-2. S2CID  124587565.
9. Карп, Ричард М. (1961-01-31). "Минимально-избыточное кодирование для дискретного канала без шума" . Труды IRE по теории информации . 7 (1). IEEE: 27–38. doi :10.1109/TIT.1961.1057615 – через IEEE.
10. Golin, Mordekai J. (январь 1998 г.). "Алгоритм динамического программирования для построения оптимальных префиксных кодов с неравной стоимостью букв" (PDF) . IEEE Transactions on Information Theory . 44 (5) (опубликовано 1998-09-01): 1770–1781. doi :10.1109/18.705558. S2CID  2265146 . Получено 10 сентября 2024 г. .
11. Ху, TC ; Такер, AC (1971). «Оптимальные деревья компьютерного поиска и алфавитные коды переменной длины». Журнал SIAM по прикладной математике . 21 (4): 514. doi :10.1137/0121057. JSTOR  2099603.
12. Кнут, Дональд Э. (1998), «Алгоритм G (алгоритм Гарсиа–Вакса для оптимальных бинарных деревьев)», Искусство программирования, т. 3: Сортировка и поиск (2-е изд.), Эддисон–Уэсли, стр. 451–453. См. также Историю и библиографию, стр. 453–454.

Библиография

• Томас Х. Кормен , Чарльз Э. Лейзерсон , Рональд Л. Ривест и Клиффорд Стайн . Введение в алгоритмы , второе издание. MIT Press и McGraw-Hill, 2001. ISBN 0-262-03293-7 . Раздел 16.3, стр. 385–392. 

Внешние ссылки

• Кодирование Хаффмана на разных языках на Rosetta Code
• Коды Хаффмана (реализация на Python)
• Визуализация кодирования Хаффмана