stringtranslate.com

эффект Магнуса

Эффект Магнуса — это явление, которое происходит, когда вращающийся объект движется через жидкость . Подъемная сила действует на вращающийся объект, и его путь может быть отклонен способом, отсутствующим, когда он не вращается. Сила и направление эффекта Магнуса зависят от скорости и направления вращения объекта. [1]

Эффект Магнуса назван в честь Генриха Густава Магнуса , немецкого физика, который его исследовал. Сила, действующая на вращающийся цилиндр, является примером подъемной силы Кутты–Жуковского , [2] названной в честь Мартина Кутты и Николая Жуковского (или Жуковского), математиков, которые внесли вклад в понимание того, как создается подъемная сила в потоке жидкости. [3]

Описание

Наиболее легко наблюдаемый случай эффекта Магнуса — когда вращающаяся сфера (или цилиндр) отклоняется от дуги, по которой она бы двигалась, если бы не вращалась. Это часто используется игроками в футбол ( соккер ) и волейбол , бейсбольными питчерами и игроками в крикет . Следовательно, это явление важно для изучения физики многих видов спорта с мячом . Это также важный фактор в изучении эффектов вращения на управляемых ракетах — и имеет некоторые инженерные применения, например, при проектировании роторных кораблей и самолетов Флеттнера .

Топспин в играх с мячом определяется как вращение вокруг горизонтальной оси, перпендикулярной направлению движения, которое перемещает верхнюю поверхность мяча в направлении движения. Под действием эффекта Магнуса топспин создает отклонение вниз движущегося мяча, большее, чем было бы создано одной лишь гравитацией. Обратное вращение создает направленную вверх силу, которая продлевает полет движущегося мяча. [4] Аналогично боковое вращение вызывает отклонение в любую сторону, как это видно во время некоторых бейсбольных питчей, например, слайдера . [5] Общее поведение похоже на поведение вокруг аэродинамического профиля (см. подъемную силу ), но с циркуляцией, создаваемой механическим вращением, а не формой фольги. [6]

В бейсболе этот эффект используется для создания нисходящего движения крученого мяча, при котором мяч вращается вперед (с «топспином»). Участники других видов спорта с мячом также пользуются этим эффектом.

Физика

Эффект Магнуса или сила Магнуса действует на вращающееся тело, движущееся относительно жидкости. Примерами служат « кривой мяч » в бейсболе или теннисный мяч, отбитый наклонно. Вращение изменяет пограничный слой между объектом и жидкостью. Сила перпендикулярна относительному направлению движения и ориентирована по направлению вращения, т. е. направлению, в котором поворачивается «нос» мяча. [7] Величина силы зависит в первую очередь от скорости вращения, относительной скорости и геометрии тела; величина также зависит от шероховатости поверхности тела и вязкости жидкости. Точные количественные предсказания силы затруднительны, [7] : 20  но, как и в других примерах аэродинамической подъемной силы, существуют более простые, качественные объяснения :

Отклонение потока

Эффект Магнуса, изображенный с вращающимся в обратном направлении цилиндром или шаром в воздушном потоке. Стрелка представляет собой результирующую подъемную силу. Извилистые линии потока представляют собой турбулентный след. Воздушный поток был отклонен в направлении вращения.
Воздух переносится вокруг объекта; это добавляется к скорости воздушного потока над объектом и вычитается снизу, что приводит к увеличению скорости воздуха сверху и уменьшению скорости воздуха снизу.

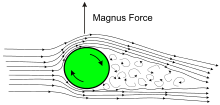
На схеме показана подъемная сила, создаваемая на вращающемся в обратном направлении шаре. След и отстающий поток воздуха были отклонены вниз; согласно третьему закону движения Ньютона, должна быть сила реакции в противоположном направлении. [1] [8]

Перепады давления

Вязкость воздуха и шероховатость поверхности объекта заставляют воздух переноситься вокруг объекта. Это увеличивает скорость воздуха с одной стороны объекта и уменьшает скорость с другой стороны. Принцип Бернулли гласит, что при определенных условиях увеличение скорости потока связано с уменьшением давления, подразумевая, что давление воздуха с одной стороны ниже, чем с другой. Эта разница давлений приводит к возникновению силы, перпендикулярной направлению движения. [9]

Подъемник Кутта–Жуковский

Вращающийся цилиндр «тянет» воздушный поток вверх, а воздух, в свою очередь, тянет цилиндр вниз, согласно третьему закону Ньютона.

На цилиндре сила, вызванная вращением, является примером подъемной силы Кутты–Жуковского . Ее можно проанализировать с точки зрения вихря, создаваемого вращением. Подъемная сила на единицу длины цилиндра является произведением скорости свободного потока (в м/с), плотности жидкости (в кг/м 3 ) и циркуляции из-за вязкостных эффектов: [2]

где сила вихря (предполагая, что окружающая жидкость подчиняется условию прилипания ) определяется выражением

[ необходима ссылка ]

где ω — угловая скорость цилиндра (в рад/с), а r — радиус цилиндра (в м).

Обратный эффект Магнуса

В исследованиях в аэродинамической трубе бейсбольные мячи (с шероховатой поверхностью) демонстрируют эффект Магнуса, а гладкие сферы — нет. [10] Дальнейшие исследования показали, что определенные комбинации условий приводят к турбулентности в жидкости с одной стороны вращающегося тела, но ламинарному потоку с другой стороны. [11] В таких случаях говорят об обратном эффекте Магнуса: отклонение противоположно отклонению при типичном эффекте Магнуса. [12]

Эффект Магнуса в потенциальном потоке

Потенциальный поток — это математическая модель стационарного потока жидкости без вязкости и завихренности . Для потенциального потока вокруг круглого цилиндра она дает следующие результаты:

Невращающийся цилиндр

Линии тока для потенциального обтекания кругового цилиндра равномерным потоком.

Картина потока симметрична относительно горизонтальной оси, проходящей через центр цилиндра. В каждой точке выше оси и соответствующей ей точке ниже оси расстояние между линиями тока одинаково, поэтому скорости также одинаковы в двух точках. Принцип Бернулли показывает, что за пределами пограничных слоев давления также одинаковы в соответствующих точках. На цилиндр не действует подъемная сила. [13]

Вращающийся цилиндр

Линии тока для потенциального потока вокруг вращающегося цилиндра. Концентрические круговые линии тока свободного вихря были наложены на параллельные линии тока равномерного потока.

Линии тока расположены ближе друг к другу непосредственно над цилиндром, чем под ним, поэтому воздух быстрее обтекает верхнюю поверхность, чем нижнюю. Принцип Бернулли показывает, что давление, прилегающее к верхней поверхности, ниже, чем давление, прилегающее к нижней поверхности. Сила Магнуса действует вертикально вверх на цилиндр. [14]

Линии тока непосредственно над цилиндром изогнуты с радиусом, немного большим радиуса цилиндра. Это означает, что вблизи верхней поверхности цилиндра имеется низкое давление. Линии тока непосредственно под цилиндром изогнуты с большим радиусом, чем линии тока над цилиндром. Это означает, что на нижнюю поверхность действует более высокое давление, чем на верхнюю. [15]

Воздух непосредственно над и под цилиндром изгибается вниз, ускоряясь градиентом давления. На воздух действует направленная вниз сила.

Третий закон Ньютона предсказывает, что сила Магнуса и направленная вниз сила, действующая на воздух, равны по величине и противоположны по направлению.

История

Эффект назван в честь немецкого физика Генриха Густава Магнуса , который продемонстрировал эффект с помощью быстро вращающегося латунного цилиндра и воздуходувки в 1852 году. [16] [17] [7] : 18  В 1672 году Исаак Ньютон размышлял об эффекте, наблюдая за теннисистами в своем кембриджском колледже. [18] [19] В 1742 году Бенджамин Робинс , британский математик, исследователь баллистики и военный инженер, объяснил отклонения в траекториях мушкетных пуль из-за их вращения. [20] [21] [22] [23]

Пионерские исследования эффекта Магнуса в аэродинамической трубе были проведены с использованием гладких вращающихся сфер в 1928 году. [24] Позднее Лайман Бриггс изучал бейсбольные мячи в аэродинамической трубе, [10] а другие получили изображения эффекта. [25] [26] [12] Исследования показывают, что турбулентный след за вращающимся мячом вызывает аэродинамическое сопротивление, плюс в следе наблюдается заметное угловое отклонение, и это отклонение происходит в направлении вращения.

В спорте

Эффект Магнуса на печально известный «удар бананом» Роберто Карлоса
Анимированная диаграмма крученого мяча 12–6

Эффект Магнуса объясняет часто наблюдаемые отклонения от типичных траекторий или путей вращающихся мячей в спорте , в частности в американском футболе , настольном теннисе , [27] теннисе , [28] волейболе , гольфе , бейсболе и крикете .

Изогнутая траектория мяча для гольфа, известная как срез или крюк, в значительной степени обусловлена ​​тем, что ось вращения мяча отклонена от горизонтали из-за совокупного эффекта угла лицевой поверхности клюшки и траектории замаха, в результате чего эффект Магнуса действует под углом, отводя мяч от прямой линии его траектории. [29] Обратное вращение (вращение верхней поверхности в обратном направлении от направления движения) мяча для гольфа вызывает вертикальную силу, которая немного противодействует силе тяжести и позволяет мячу оставаться в воздухе немного дольше, чем если бы мяч не вращался: это позволяет мячу пролететь большее расстояние, чем мячу, не вращающемуся вокруг своей горизонтальной оси. [ необходима ссылка ]

В настольном теннисе эффект Магнуса легко наблюдать из-за малой массы и низкой плотности мяча. Опытный игрок может придать мячу самые разные вращения. Ракетки для настольного тенниса обычно имеют поверхность из резины, чтобы обеспечить ракетке максимальное сцепление с мячом и придать вращение.

В крикете эффект Магнуса способствует типам движения, известным как дрейф , падение и подъем в спин-боулинге , в зависимости от оси вращения вращения, приложенного к шару. Эффект Магнуса не отвечает за движение, наблюдаемое в обычном свинг-боулинге , [30] : Рис. 4.19  , в котором градиент давления вызван не вращением шара, а его приподнятым швом и асимметричной шероховатостью или гладкостью двух его половин; однако эффект Магнуса может быть ответственен за так называемый «Малинга-свинг», [31] [32] , который наблюдался в боулинге игрока в свинг-боулинг Ласита Малинги .

В страйкболе для создания обратного вращения стреляной пули используется система, известная как хоп-ап , что значительно увеличивает дальность ее полета, используя эффект Магнуса аналогично тому, как это делается в гольфе.

В бейсболе питчеры часто придают мячу различные вращения, заставляя его изгибаться в желаемом направлении из-за эффекта Магнуса. Система PITCHf/x измеряет изменение траектории, вызванное Магнусом во всех бросках в Главной лиге бейсбола . [33]

Мяч для чемпионата мира по футболу FIFA 2010 года критиковали за эффект Магнуса, отличный от предыдущих мячей. Мяч описывали как имеющий меньший эффект Магнуса и, как следствие, летящий дальше, но с менее контролируемым отклонением. [34]

Во внешней баллистике

Эффект Магнуса также можно найти в продвинутой внешней баллистике . Во-первых, вращающаяся пуля в полете часто подвергается воздействию бокового ветра , который можно упростить как дующий слева или справа. В дополнение к этому, даже в совершенно спокойном воздухе пуля испытывает небольшую боковую составляющую ветра из-за ее рыскающего движения. Это рыскающее движение вдоль траектории полета пули означает, что нос пули указывает в несколько ином направлении от направления движения пули. Другими словами, пуля «скользит» вбок в любой момент и, таким образом, испытывает небольшую боковую составляющую ветра в дополнение к любой боковой составляющей ветра. [35]

Объединенный боковой компонент ветра этих двух эффектов вызывает действие силы Магнуса на пулю, которая перпендикулярна как направлению, в которое направлена ​​пуля, так и объединенному боковому ветру. В очень простом случае, когда мы игнорируем различные усложняющие факторы, сила Магнуса от бокового ветра вызовет действие силы, направленной вверх или вниз, на вращающуюся пулю (в зависимости от левого или правого ветра и вращения), вызывая отклонение траектории полета пули вверх или вниз, тем самым влияя на точку попадания.

В целом, влияние силы Магнуса на траекторию полета пули обычно незначительно по сравнению с другими силами, такими как аэродинамическое сопротивление . Однако оно сильно влияет на устойчивость пули, которая, в свою очередь, влияет на величину сопротивления, на то, как пуля ведет себя при ударе, и на многие другие факторы. Устойчивость пули страдает, поскольку эффект Магнуса действует на центр давления пули, а не на ее центр тяжести . [36] Это означает, что он влияет на угол рыскания пули; он имеет тенденцию закручивать пулю вдоль ее траектории полета, либо по направлению к оси полета (уменьшая рыскание, тем самым стабилизируя пулю), либо от оси полета (увеличивая рыскание, тем самым дестабилизируя пулю). Критическим фактором является расположение центра давления, которое зависит от структуры поля потока, которая, в свою очередь, зависит главным образом от скорости пули (сверхзвуковая или дозвуковая), а также от формы, плотности воздуха и особенностей поверхности. Если центр давления находится впереди центра тяжести, эффект дестабилизирующий; если центр давления находится позади центра тяжести, эффект стабилизирующий. [37]

В авиации

Роторный самолет Антона Флеттнера

Некоторые самолеты были построены с использованием эффекта Магнуса для создания подъемной силы с вращающимся цилиндром вместо крыла, что позволяет летать на более низких горизонтальных скоростях. [2] Самая ранняя попытка использовать эффект Магнуса для самолета тяжелее воздуха была предпринята в 1910 году членом Конгресса США Батлером Эймсом из Массачусетса. Следующая попытка была предпринята в начале 1930-х годов тремя изобретателями из штата Нью-Йорк. [38]

Движение и стабилизация судна

E-Ship 1 с установленными роторами Флеттнера

В роторных судах для движения используются цилиндры, похожие на мачты, называемые роторами Флеттнера . Они устанавливаются вертикально на палубе судна. Когда ветер дует сбоку, эффект Магнуса создает прямую тягу. Таким образом, как и любое парусное судно, роторное судно может двигаться вперед только при наличии ветра. Этот эффект также используется в специальном типе корабельного стабилизатора, состоящего из вращающегося цилиндра, установленного под ватерлинией и выходящего сбоку. Управляя направлением и скоростью вращения, можно создать сильную подъемную или прижимную силу . [39] Самое крупное развертывание системы на сегодняшний день - на моторной яхте Eclipse .

Смотрите также

Ссылки

  1. ^ ab Halliday, David (1988). Fundamentals of Physics (3rd Extended ed.). John Wiley and Sons. стр. E6–E8. В результате след не симметричен; воздушный поток отклоняется в одну сторону, а сфера испытывает силу реакции в противоположном направлении... Направление и величина этой силы будут зависеть от скорости и направления вращения. Это явление известно как эффект Магнуса...
  2. ^ abc "Подъемная сила на вращающихся цилиндрах". NASA Glenn Research Center. 9 ноября 2010 г. Архивировано из оригинала 11 января 2014 г. Получено 7 ноября 2013 г.
  3. ^ Андерсон, Джон Д. (1984) Основы аэродинамики , разделы 3.15 и 3.16. McGraw-Hill ISBN 0-07-001656-9
  4. ^ «Почему мячи для гольфа имеют ямочки?». math.ucr.edu .
  5. ↑ Curveball. Архивировано 21 октября 2012 г. на Wayback Machine , Физика бейсбола.
  6. ^ Клэнси, Л.Дж. (1975), Аэродинамика , Раздел 4.6, Pitman Publishing
  7. ^ abc Seifert, Jost (ноябрь 2012 г.). «Обзор эффекта Магнуса в аэронавтике». Progress in Aerospace Sciences . 55 : 17–45. Bibcode : 2012PrAeS..55...17S. doi : 10.1016/j.paerosci.2012.07.001.
  8. ^ Glenn Research Center. "Что такое подъемная сила?" . Получено 20 сентября 2024 г. Подъемная сила возникает, когда движущийся поток газа поворачивается твердым объектом. Поток поворачивается в одном направлении, а подъемная сила создается в противоположном направлении, согласно третьему закону Ньютона о действии и противодействии.
  9. ^ Холлидей, Дэвид (1988). Основы физики (3-е расширенное изд.). John Wiley and Sons. стр. 278–279. Без вязкости и пограничного слоя вращающийся мяч не мог бы переносить воздух таким образом... скорость воздуха под мячом меньше, чем над мячом. Из уравнения Бернулли давление воздуха под мячом должно быть больше, чем над мячом, поэтому мяч испытывает динамическую подъемную силу.
  10. ^ ab Briggs, Lyman J. (ноябрь 1959 г.). «Влияние вращения и скорости на боковое отклонение (кривую) бейсбольного мяча; и эффект Магнуса для гладких сфер». American Journal of Physics . 27 (8): 589–596. Bibcode : 1959AmJPh..27..589B. doi : 10.1119/1.1934921.
  11. ^ Ким, Джуха; Чхве, Хэчон; Пак, Хёнмин; Ю, Чон Юль ( 10 сентября 2014 г.). «Обратный эффект Магнуса на вращающейся сфере: когда и почему». Журнал механики жидкости . 754. Bibcode : 2014JFM...754R...2K. doi : 10.1017/jfm.2014.428.
  12. ^ ab Cross, Rod. "Фотографии в аэродинамической трубе" (PDF) . Физический факультет Сиднейского университета. стр. 4 . Получено 10 февраля 2013 г. .
  13. ^ «Из симметрии линий тока ясно, что скорость воздуха одинакова в соответствующих точках над и под мячом, ...»
    «Из уравнения Бернулли мы затем выводим, что давление в таких соответствующих точках одинаково и что воздух не оказывает на мяч никакой силы, направленной вверх или вниз в силу своего движения; динамическая подъемная сила равна нулю». Резник и Холлидей (1966), ФИЗИКА , Раздел 18-5
  14. ^ «Когда на объекте возникает динамическая подъемная сила, она всегда связана с несимметричным набором линий тока, относительно близко расположенных друг к другу с одной стороны и относительно далеко друг от друга с другой... которые соответствуют... циркуляции жидкости вокруг объекта».
    «[линии тока] ближе друг к другу над [телом], чем под ним, так что принцип Бернулли предсказывает наблюдаемую динамическую подъемную силу». Резник и Холлидей (1966), ФИЗИКА , раздел 18-5
  15. ^ Бабинский, Хольгер (ноябрь 2003 г.). «Как работают крылья?». Physics Education . 38 (6): 497–503. Bibcode : 2003PhyEd..38..497B. doi : 10.1088/0031-9120/38/6/001. ...если линия тока изогнута, должен быть градиент давления поперек линии тока
  16. ^ Магнус, Г. (1852). «Über die Abweichung der Geschosse» [Об отклонении снарядов]. Abhandlungen der Königlichen Akademie der Wissenschaften zu Berlin (на немецком языке): 1–23 – через Библиотеку наследия биоразнообразия .
  17. ^ Магнус, Г. (январь 1853 г.). «Ueber die Abweichung der Geschosse, und: Ueber eine auffallende Erscheinung bei rotirenden Körpern» [Об отклонении снарядов и: О явлении погружения среди вращающихся тел]. Аннален дер Физик (на немецком языке). 164 (1): 1–29. Бибкод : 1853АнП...164....1М. дои : 10.1002/andp.18531640102.
  18. ↑ Ньютон, Исаак (19 февраля 1672 г.). «Письмо г-на Исаака Ньютона, профессора математики Кембриджского университета; содержащее его новую теорию о свете и цветах: отправлено автором издателю из Кембриджа 6 февраля 1671/72 г.; для передачи в Королевское общество». Philosophical Transactions of the Royal Society of London . 6 (80): 3075–3087. doi :10.1098/rstl.1671.0072.
  19. ^ Глейк, Джеймс. 2004. Исаак Ньютон. Лондон: Harper Fourth Estate. [ нужна страница ]
  20. ^ Бенджамин Робинс, Новые принципы артиллерийского дела: содержащие определения силы пороха и исследования разницы в силе сопротивления воздуха быстрым и медленным движениям (Лондон: J. Nourse, 1742). (На стр. 208 издания 1805 года « Новых принципов артиллерийского дела » Робинса Робинс описывает эксперимент, в котором он наблюдал эффект Магнуса: шар был подвешен на тросе, состоящем из двух скрученных вместе нитей, и шар был приведен в движение. По мере того, как нити разматывались, качающийся шар вращался, и плоскость его качания также вращалась. Направление вращения плоскости зависело от направления вращения шара.)
  21. ↑ Том Холмберг, «Артиллерия качается, как маятник...» в «Серии Наполеона»
  22. ^ Стил, Бретт Д. (1994). «Мушкеты и маятники: Бенджамин Робинс, Леонард Эйлер и революция в баллистике». Технология и культура . 35 (2): 348–382. doi :10.1353/tech.1994.0084. JSTOR  3106305. Проект MUSE  887921.
  23. ↑ Наблюдения Ньютона и Робинса над эффектом Магнуса воспроизведены в: Питер Гатри Тейт (1893) «О пути вращающегося сферического снаряда», Труды Королевского общества Эдинбурга , т. 37, стр. 427–440.
  24. ^ Maccoll, John W. (сентябрь 1928). «Аэродинамика вращающейся сферы». Журнал Королевского авиационного общества . 32 (213): 777–798. doi :10.1017/S0368393100136260.
  25. ^ Браун, Ф. (1971). См. «Дуновение ветра» . Университет Нотр-Дам.{{cite book}}: CS1 maint: location missing publisher (link)
  26. ^ Ван Дайк, Милтон (1982). Альбом Fluid motion . Стэнфордский университет.{{cite book}}: CS1 maint: location missing publisher (link)
  27. ^ «Определение эффекта Магнуса в настольном теннисе». sidesandnets.com . 23 апреля 2021 г. . Получено 23 апреля 2021 г. .
  28. ↑ Лорд Рэлей (1877) «О нерегулярном полете теннисного мяча», Вестник математики , т. 7, стр. 14–16.
  29. ^ «Ось вращения». Трекмэн Гольф . 17 ноября 2015 г.
  30. ^ Клэнси, Л. Дж. (1975). Аэродинамика . Лондон: Pitman Publishing Limited. ISBN 0-273-01120-0.
  31. ^ Мехта, РД (2007). «Уникальный замах Малинги». The Wisden Cricketer . Том 4, № 10. С. 23. ISSN  1740-9519.
  32. ^ Mehta, RD (2014). Механика жидкости при замахе мяча в крикете . 19-я Австралазийская конференция по механике жидкости. Том 1. Мельбурн: Австралазийское общество механики жидкости. С. 1–8. ISBN 978-1-5108-2684-7. S2CID  34183383.
  33. ^ Натан, Алан М. (18 октября 2012 г.). «Определение движения высоты тона по данным PITCHf/x» (PDF) .[ самостоятельно опубликованный источник? ]
  34. ^ Интервью на SBS 2010 FIFA World Cup Show 22 июня 2010 г. 10:30 вечера от Крейга Джонстона
  35. ^ Рупрехт Неннстиль. «Рыскание покоя». Nennstiel-ruprecht.de . Проверено 22 февраля 2013 г.
  36. ^ "Математическое моделирование траекторий снарядов под влиянием эффектов окружающей среды, Райан Ф. Хук,∗Университет Нового Южного Уэльса в Канберре при Академии австралийских сил обороны, 2612, Австралия". Архивировано из оригинала 4 февраля 2018 года . Получено 2 февраля 2018 года .
  37. ^ Том Бенсон. «Условия устойчивости ракеты». Архивировано из оригинала 13 мая 2013 года . Получено 29 августа 2014 года .
  38. ^ "Вихревые катушки поднимают этот самолет". Popular Science . Ноябрь 1930. С. 26. Получено 9 мая 2021 г.
  39. ^ "Quantum Rotary Stabilizers". YouTube . 2 июня 2009 г. Архивировано из оригинала 21 июля 2013 г.

Дальнейшее чтение

Внешние ссылки

На Викискладе есть медиафайлы по теме «Эффект Магнуса» .