Прецессия

Периодическое изменение направления оси вращения

Прецессия гироскопа [ ^{требуется разъяснение ]}

  Вращение

  Прецессия

  Нутация

в наклонении планеты

Прецессия — это изменение ориентации оси вращения вращающегося тела. В соответствующей системе отсчета ее можно определить как изменение первого угла Эйлера , тогда как третий угол Эйлера определяет само вращение . Другими словами, если ось вращения тела сама вращается вокруг второй оси, то говорят, что тело прецессирует вокруг второй оси. Движение, при котором изменяется второй угол Эйлера, называется нутацией . В физике существует два типа прецессии: без крутящего момента и с крутящим моментом.

В астрономии прецессия относится к любому из нескольких медленных изменений вращательных или орбитальных параметров астрономического тела. Важным примером является устойчивое изменение ориентации оси вращения Земли , известное как прецессия равноденствий .

Без крутящего момента или без крутящего момента

Прецессия без крутящего момента подразумевает, что к телу не прикладывается внешний момент (крутящий момент). При прецессии без крутящего момента момент импульса является постоянной величиной, но вектор угловой скорости меняет ориентацию со временем. Это возможно благодаря изменяющемуся во времени моменту инерции или, точнее, изменяющейся во времени матрице инерции . Матрица инерции состоит из моментов инерции тела, вычисленных относительно отдельных осей координат (например, x , y , z ). Если объект асимметричен относительно своей главной оси вращения, момент инерции относительно каждого направления координат будет изменяться со временем, сохраняя при этом момент импульса. В результате составляющая угловых скоростей тела относительно каждой оси будет изменяться обратно пропорционально моменту инерции каждой оси.

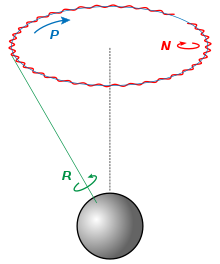
Скорость прецессии без крутящего момента объекта с осью симметрии, например, диска, вращающегося вокруг оси, не совпадающей с этой осью симметрии, можно рассчитать следующим образом: ^[1] где ω _p — скорость прецессии, ω _s — скорость вращения вокруг оси симметрии, I _s — момент инерции относительно оси симметрии, I _p — момент инерции относительно любой из двух других равных перпендикулярных главных осей, а α — угол между направлением момента инерции и осью симметрии. ^[2] $${\displaystyle {\boldsymbol {\omega }}_{\mathrm {p} }={\frac {{\boldsymbol {I}}_{\mathrm {s} }{\boldsymbol {\omega }}_{\mathrm {s} }}{{\boldsymbol {I}}_{\mathrm {p} }\cos({\boldsymbol {\alpha }})}}}$$

Если объект не является идеально жестким , неупругая диссипация будет стремиться демпфировать прецессию без крутящего момента ^[3] , а ось вращения будет совпадать с одной из осей инерции тела.

Для обычного твердого объекта без какой-либо оси симметрии эволюция ориентации объекта, представленная (например) матрицей вращения R , преобразующей внутренние координаты во внешние, может быть численно смоделирована. Учитывая фиксированный внутренний момент инерции тензора объекта I ₀ и фиксированный внешний угловой момент L , мгновенная угловая скорость равна Прецессия происходит путем многократного пересчета ω и применения малого вектора вращения ω dt на короткое время dt ; например: для кососимметричной матрицы [ ω ] _× . Ошибки, вызванные конечными временными шагами, имеют тенденцию увеличивать вращательную кинетическую энергию: эта нефизическая тенденция может быть нейтрализована путем многократного применения малого вектора вращения v, перпендикулярного как ω, так и L , отметив, что $${\displaystyle {\boldsymbol {\omega }}\left({\boldsymbol {R}}\right)={\boldsymbol {R}}{\boldsymbol {I}}_{0}^{-1}{\boldsymbol {R}}^{T}{\boldsymbol {L}}}$$ $${\displaystyle {\boldsymbol {R}}_{\text{new}}=\exp \left(\left[{\boldsymbol {\omega }}\left({\boldsymbol {R}}_{\text{old}}\right)\right]_{\times }dt\right){\boldsymbol {R}}_{\text{old}}}$$ $${\displaystyle E\left({\boldsymbol {R}}\right)={\boldsymbol {\omega }}\left({\boldsymbol {R}}\right)\cdot {\frac {\boldsymbol {L}}{2}}}$$ $${\displaystyle E\left(\exp \left(\left[{\boldsymbol {v}}\right]_{\times }\right){\boldsymbol {R}}\right)\approx E\left({\boldsymbol {R}}\right)+\left({\boldsymbol {\omega }}\left({\boldsymbol {R}}\right)\times {\boldsymbol {L}}\right)\cdot {\boldsymbol {v}}}$$

Крутящий момент, вызванный

Прецессия, вызванная крутящим моментом ( гироскопическая прецессия ), — это явление, при котором ось вращающегося объекта (например, гироскопа ) описывает конус в пространстве, когда к нему приложен внешний крутящий момент . Это явление обычно наблюдается во вращающемся игрушечном волчке , но прецессии могут подвергаться все вращающиеся объекты. Если скорость вращения и величина внешнего крутящего момента постоянны, ось вращения будет двигаться под прямым углом к ​​направлению , которое интуитивно следует из внешнего крутящего момента. В случае игрушечного волчка его вес действует вниз от его центра масс , а нормальная сила (реакция) земли толкает его вверх в точке контакта с опорой. Эти две противоположные силы создают крутящий момент, который заставляет волчок прецессировать.

Реакция вращающейся системы на приложенный крутящий момент. Когда устройство поворачивается и добавляется некоторый крен, колесо имеет тенденцию к наклону.

Устройство, изображенное справа, установлено на карданном подвесе . Изнутри наружу расположены три оси вращения: ступица колеса, ось карданного подвеса и вертикальный шарнир.

Чтобы различать две горизонтальные оси, вращение вокруг ступицы колеса будет называться вращением , а вращение вокруг оси карданного подвеса будет называться тангажем . Вращение вокруг вертикальной оси поворота называется вращением .

Сначала представьте, что все устройство вращается вокруг (вертикальной) оси вращения. Затем добавляется вращение колеса (вокруг ступицы колеса). Представьте, что ось карданного подвеса заблокирована, так что колесо не может наклоняться. Ось карданного подвеса имеет датчики, которые измеряют, есть ли крутящий момент вокруг оси карданного подвеса.

На рисунке часть колеса обозначена как dm ₁ . В изображенный момент времени часть dm ₁ находится на периметре вращательного движения вокруг (вертикальной) оси вращения. Следовательно, часть dm ₁ имеет большую угловую скорость вращения относительно вращения вокруг оси вращения, и поскольку dm ₁ принудительно приближается к оси вращения (колесо вращается дальше), из-за эффекта Кориолиса , относительно вертикальной оси вращения dm ₁ стремится двигаться в направлении верхней левой стрелки на диаграмме (показанной под углом 45°) в направлении вращения вокруг оси вращения. ^[4] Часть dm ₂ колеса движется от оси вращения, и поэтому сила (снова сила Кориолиса) действует в том же направлении, что и в случае dm ₁ . Обратите внимание, что обе стрелки указывают в одном направлении.

Те же рассуждения применимы и к нижней половине колеса, но там стрелки указывают в противоположном направлении от верхних стрелок. В совокупности по всему колесу возникает крутящий момент вокруг оси кардана, когда к вращению вокруг вертикальной оси добавляется некоторое вращение.

Важно отметить, что крутящий момент вокруг оси карданного подвеса возникает без какой-либо задержки, реакция мгновенная.

В приведенном выше обсуждении установка сохранялась неизменной за счет предотвращения качания вокруг оси карданного подвеса. В случае с вращающимся волчком, когда волчок начинает наклоняться, гравитация создает крутящий момент. Однако вместо того, чтобы перевернуться, волчок просто немного наклоняется. Это качающееся движение переориентирует волчок относительно прилагаемого крутящего момента. Результатом является то, что крутящий момент, оказываемый гравитацией — через качающееся движение — вызывает гироскопическую прецессию (которая, в свою очередь, создает встречный крутящий момент против крутящего момента гравитации), а не заставляет волчок падать на бок.

Прецессия или гироскопические соображения влияют на производительность велосипеда на высокой скорости. Прецессия также является механизмом, лежащим в основе гирокомпасов .

Классический (ньютоновский)

Крутящий момент, вызванный нормальной силой – F _g и весом волчка, вызывает изменение углового момента L в направлении этого крутящего момента. Это заставляет волчок прецессировать.

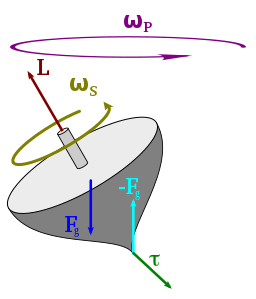
Прецессия — это изменение угловой скорости и углового момента, вызванное крутящим моментом. Общее уравнение, связывающее крутящий момент со скоростью изменения углового момента, имеет вид: где и — векторы крутящего момента и углового момента соответственно. $${\displaystyle {\boldsymbol {\tau }}={\frac {\mathrm {d} \mathbf {L} }{\mathrm {d} t}}}$$ ${\displaystyle {\boldsymbol {\tau }}}$ ${\displaystyle \mathbf {L} }$

Из-за способа определения векторов крутящего момента, это вектор, который перпендикулярен плоскости сил, которые его создают. Таким образом, можно видеть, что вектор углового момента будет изменяться перпендикулярно этим силам. В зависимости от того, как создаются силы, они часто будут вращаться вместе с вектором углового момента, и тогда создается круговая прецессия.

При этих обстоятельствах угловая скорость прецессии определяется по формуле: ^[5]

${\displaystyle {\boldsymbol {\omega }}_{\mathrm {p} }={\frac {\ mgr}{I_{\mathrm {s} }{\boldsymbol {\omega }}_{\mathrm {s} }}}={\frac {\tau }{I_{\mathrm {s} }{\boldsymbol {\omega }}_{\mathrm {s} }\sin(\theta )}}}$

где I _s — момент инерции , ω _s — угловая скорость вращения вокруг оси вращения, m — масса, g — ускорение силы тяжести, θ — угол между осью вращения и осью прецессии, а r — расстояние между центром масс и точкой опоры. Вектор крутящего момента начинается в центре масс. Используя ω = ⁠2π/Т⁠ , мы находим, что период прецессии определяется по формуле: ^[6] $${\displaystyle T_{\mathrm {p} }={\frac {4\pi ^{2}I_{\mathrm {s} }}{\ mgrT_{\mathrm {s} }}}={\frac {4\pi ^{2}I_{\mathrm {s} }\sin(\theta )}{\ \tau T_{\mathrm {s} }}}}$$

Где I _s — момент инерции , T _s — период вращения вокруг оси вращения, а τ — крутящий момент . В общем случае проблема сложнее.

Релятивистский (эйнштейновский)

Специальная и общая теории относительности дают три типа поправок к ньютоновской прецессии гироскопа вблизи большой массы, такой как Земля, описанной выше. Они следующие:

• Прецессия Томаса — специальная релятивистская поправка, учитывающая ускорение объекта (например, гироскопа) по криволинейной траектории.
• Прецессия де Ситтера — общерелятивистская поправка, учитывающая метрику Шварцшильда искривленного пространства вблизи большой невращающейся массы.
• Прецессия Лензе–Тирринга — общерелятивистская поправка, учитывающая увлечение системы отсчета метрикой Керра искривленного пространства вблизи большой вращающейся массы.

Геодезические линии Шварцшильда (иногда прецессия Шварцшильда) используются для прогнозирования аномальной прецессии перигелия планет, в частности для точного прогнозирования прецессии апсид Меркурия.

Астрономия

В астрономии прецессия относится к любому из нескольких вызванных гравитацией, медленных и непрерывных изменений оси вращения астрономического тела или орбитальной траектории. Прецессия равноденствий, прецессия перигелия, изменения наклона оси Земли к ее орбите и эксцентриситет ее орбиты на протяжении десятков тысяч лет являются важными частями астрономической теории ледниковых периодов . (См. циклы Миланковича .)

Аксиальная прецессия (прецессия равноденствий)

Осевая прецессия — это движение оси вращения астрономического тела, при котором ось медленно описывает конус. В случае Земли этот тип прецессии также известен как прецессия равноденствий , лунно-солнечная прецессия или прецессия экватора . Земля проходит один такой полный прецессионный цикл за период приблизительно 26 000 лет или 1° каждые 72 года, в течение которых положения звезд будут медленно меняться как в экваториальных координатах , так и в эклиптической долготе . В течение этого цикла северный осевой полюс Земли перемещается из того места, где он находится сейчас, в пределах 1° от Полярной звезды , по окружности вокруг эклиптического полюса с угловым радиусом около 23,5°.

Древнегреческий астроном Гиппарх (ок. 190–120 гг. до н. э.) обычно считается самым ранним известным астрономом, распознавшим и оценившим прецессию равноденствий примерно на 1° за столетие (что недалеко от фактического значения для древности, 1,38°), ^[7] хотя есть некоторые незначительные споры о том, был ли он таковым. ^[8] В Древнем Китае ученый-чиновник династии Цзинь Юй Си ( ок. 307–345 гг. н. э.) сделал похожее открытие столетия спустя, отметив, что положение Солнца во время зимнего солнцестояния смещалось примерно на один градус в течение пятидесяти лет относительно положения звезд. ^[9] Прецессия земной оси была позже объяснена ньютоновской физикой . Будучи сплющенным сфероидом , Земля имеет несферическую форму, выпячиваясь наружу на экваторе. Гравитационные приливные силы Луны и Солнца прикладывают крутящий момент к экватору, пытаясь втянуть экваториальную выпуклость в плоскость эклиптики , но вместо этого заставляя ее прецессировать. Крутящий момент, создаваемый планетами, особенно Юпитером , также играет свою роль. ^[10]

Прецессионное движение оси (слева), прецессия равноденствия по отношению к далеким звездам (посередине) и путь северного небесного полюса среди звезд из-за прецессии. Вега — яркая звезда внизу (справа).

Апсидальная прецессия

Прецессия апсид — орбита постепенно вращается с течением времени.

Орбиты планет вокруг Солнца на самом деле не следуют каждый раз одинаковому эллипсу, а фактически очерчивают форму лепестка цветка, поскольку большая ось эллиптической орбиты каждой планеты также прецессирует в своей орбитальной плоскости, отчасти в ответ на возмущения в виде изменяющихся гравитационных сил, оказываемых другими планетами. Это называется прецессией перигелия или апсидальной прецессией .

На дополнительном изображении показана прецессия апсид Земли. По мере того, как Земля движется вокруг Солнца, ее эллиптическая орбита постепенно вращается с течением времени. Эксцентриситет ее эллипса и скорость прецессии ее орбиты преувеличены для наглядности. Большинство орбит в Солнечной системе имеют гораздо меньший эксцентриситет и прецессируют с гораздо меньшей скоростью, что делает их почти круговыми и почти неподвижными.

Расхождения между наблюдаемой скоростью прецессии перигелия планеты Меркурий и предсказанной классической механикой были заметными среди форм экспериментальных доказательств, приведших к принятию теории относительности Эйнштейна (в частности, его общей теории относительности ), которая точно предсказала аномалии. ^{[11] [12]} Отклоняясь от закона Ньютона, теория тяготения Эйнштейна предсказывает дополнительный член ⁠А/г ⁴⁠ , что точно дает наблюдаемую избыточную скорость вращения в 43 угловые секунды каждые 100 лет.

Узловая прецессия

Орбитальные узлы также прецессируют с течением времени.

Смотрите также

• прецессия Лармора
• Нутация
• Полярное движение
• Прецессия (механическая)
• Прецессия как форма параллельного транспорта

Ссылки

1. Шауб, Ханспетер (2003), Аналитическая механика космических систем, AIAA, стр. 149–150, ISBN 9781600860270
2. Боал, Дэвид (2001). "Лекция 26 – Вращение без крутящего момента – оси, закрепленные на теле" (PDF) . Получено 17 сентября 2008 г.
3. Шарма, Ишан; Бернс, Джозеф А.; Хуэй, К.-Х. (2005). "Время нутационного затухания в твердых телах вращения". Monthly Notices of the Royal Astronomical Society . 359 (1): 79. Bibcode : 2005MNRAS.359...79S. doi : 10.1111/j.1365-2966.2005.08864.x .
4. Теодореску, Петре П. (2002). Механические системы, классические модели: Том II: Механика дискретных и непрерывных систем. Springer Science & Business Media. стр. 420. ISBN 978-1-4020-8988-6.
5. Мёбс, Уильям; Линг, Сэмюэл Дж.; Сэнни, Джефф (19 сентября 2016 г.). 11.4 Прецессия гироскопа — университетская физика, том 1 | OpenStax. Хьюстон, Техас . Получено 23 октября 2020 г.{{cite book}}: CS1 maint: location missing publisher (link)
6. Мёбс, Уильям; Линг, Сэмюэл Дж.; Сэнни, Джефф (19 сентября 2016 г.). 11.4 Прецессия гироскопа — университетская физика, том 1 | OpenStax. Хьюстон, Техас . Получено 23 октября 2020 г.{{cite book}}: CS1 maint: location missing publisher (link)
7. Барбьери, Чезаре (2007). Основы астрономии . Нью-Йорк: Taylor and Francis Group. стр. 71. ISBN 978-0-7503-0886-1.
8. Свердлов, Ноэль (1991). О космических тайнах Митры . Классическая филология, 86, (1991), 48–63. стр. 59.
9. Сан, Квок. (2017). Наше место во Вселенной: понимание фундаментальной астрономии из древних открытий , второе издание. Чам, Швейцария: Springer. ISBN 978-3-319-54171-6 , стр. 120; см. также Нидхэм, Джозеф; Ван, Лин. (1995) [1959]. Наука и цивилизация в Китае: математика и науки о небесах и земле , т. 3, переиздание. Кембридж: Cambridge University Press. ISBN 0-521-05801-5 , стр. 220.  
10. Bradt, Hale (2007). Методы астрономии . Cambridge University Press . стр. 66. ISBN 978-0-521-53551-9.
11. Макс Борн (1924), Теория относительности Эйнштейна (издание Дувра 1962 года, страница 348 содержит таблицу, документирующую наблюдаемые и вычисленные значения прецессии перигелия Меркурия, Венеры и Земли.)
12. "Было обнаружено еще большее значение прецессии для черной дыры на орбите вокруг гораздо более массивной черной дыры, составляющее 39 градусов на каждой орбите". 18 марта 2008 г. Архивировано из оригинала 2018-08-07 . Получено 2023-11-15 .{{cite web}}: CS1 maint: bot: original URL status unknown (link)

Внешние ссылки

• Медиа, связанные с прецессией на Wikimedia Commons
• Объяснение и вывод формулы прецессии волчка
• Прецессия и теория Миланковича От звездочетов до звездолетов