Интерференция волн

Явление, возникающее в результате суперпозиции двух волн

Интерференция двух волн. В фазе : две нижние волны объединяются (левая панель), в результате чего образуется волна с добавленной амплитудой (конструктивная интерференция) . В противофазе : (здесь на 180 градусов) две нижние волны объединяются (правая панель), в результате чего образуется волна с нулевой амплитудой (деструктивная интерференция) .

В физике интерференция — это явление, при котором две когерентные волны объединяются путем сложения их интенсивностей или смещений с учетом разности фаз . Результирующая волна может иметь большую интенсивность ( конструктивная интерференция ) или меньшую амплитуду ( деструктивная интерференция ), если две волны находятся в фазе или в противофазе соответственно. Эффекты интерференции можно наблюдать со всеми типами волн, например, световыми , радио , акустическими , поверхностными водными волнами , гравитационными волнами или волнами материи , а также в громкоговорителях в виде электрических волн.

Этимология

Слово «интерференция» происходит от латинских слов inter , что означает «между», и fere , что означает «удар или удар», и было использовано в контексте суперпозиции волн Томасом Юнгом в 1801 году. ^{[1] [2] [3]}

Механизмы

Интерференция право-бегущей (зеленой) и лево-бегущей (синей) волн в двумерном пространстве, приводящая к образованию конечной (красной) волны

Интерференция волн от двух точечных источников.

Обрезанная анимация томографического сканирования интерференции лазерного света, проходящего через два отверстия (боковые края).

Принцип суперпозиции волн гласит, что когда две или более распространяющихся волны одного типа падают на одну и ту же точку, результирующая амплитуда в этой точке равна векторной сумме амплитуд отдельных волн. ^[4] Если гребень волны встречается с гребнем другой волны той же частоты в той же точке, то амплитуда равна сумме отдельных амплитуд — это конструктивная интерференция. Если гребень одной волны встречается с впадиной другой волны, то амплитуда равна разнице отдельных амплитуд — это известно как деструктивная интерференция. В идеальных средах (вода, воздух почти идеальны) энергия всегда сохраняется, в точках деструктивной интерференции амплитуды волн компенсируют друг друга, и энергия перераспределяется в другие области. Например, когда два камешка падают в пруд, можно наблюдать закономерность; но в конечном итоге волны продолжаются, и только когда они достигают берега, энергия поглощается средой.

Фотография области мыльной пленки размером 1,5 см x 1 см под белым светом. Различная толщина пленки и геометрия наблюдения определяют, какие цвета подвергаются конструктивной или деструктивной интерференции. Мелкие пузырьки существенно влияют на толщину окружающей пленки.

Конструктивная интерференция происходит, когда разность фаз между волнами четно кратна π (180°), тогда как деструктивная интерференция происходит, когда разность фаз является нечетно кратной π . Если разность фаз является промежуточной между этими двумя крайностями, то величина смещения суммированных волн лежит между минимальным и максимальным значениями.

Рассмотрим, например, что происходит, когда два одинаковых камня падают в неподвижный бассейн с водой в разных местах. Каждый камень генерирует круговую волну, распространяющуюся наружу от точки, куда был брошен камень. Когда две волны накладываются, чистое смещение в определенной точке является суммой смещений отдельных волн. В некоторых точках они будут находиться в фазе и дадут максимальное смещение. В других местах волны будут в противофазе, и чистого смещения в этих точках не будет. Таким образом, части поверхности будут неподвижны — они видны на рисунке выше и справа как неподвижные сине-зеленые линии, исходящие из центра.

Интерференция света — уникальное явление, поскольку мы никогда не можем наблюдать суперпозицию электромагнитного поля напрямую, как, например, в воде. Суперпозиция в электромагнитном поле — это предполагаемое явление, необходимое для объяснения того, как два световых луча проходят друг сквозь друга и продолжают свой путь. Яркими примерами интерференции света являются знаменитый эксперимент с двумя щелями , лазерный спекл , антибликовые покрытия и интерферометры .

Помимо классической волновой модели для понимания оптической интерференции, квантовые волны материи также демонстрируют интерференцию.

Действительные волновые функции

Вышеизложенное можно продемонстрировать в одном измерении, выведя формулу для суммы двух волн. Уравнение для амплитуды синусоидальной волны, распространяющейся вправо вдоль оси x, имеет вид где — пиковая амплитуда, — волновое число , — угловая частота волны. Предположим, что вторая волна той же частоты и амплитуды, но с другой фазой также распространяется вправо, где — разность фаз между волнами в радианах . Две волны наложатся и сложатся: сумма двух волн равна Используя тригонометрическое тождество для суммы двух косинусов: это можно записать Это представляет собой волну на исходной частоте, распространяющуюся вправо, как и ее компоненты, амплитуда которой пропорциональна косинусу . $${\displaystyle W_{1}(x,t)=A\cos(kx-\omega t)}$$ ${\displaystyle A}$ ${\displaystyle k=2\pi /\lambda }$ ${\displaystyle \omega =2\pi f}$ $${\displaystyle W_{2}(x,t)=A\cos(kx-\omega t+\varphi )}$$ ${\displaystyle \varphi }$ $${\displaystyle W_{1}+W_{2}=A[\cos(kx-\omega t)+\cos(kx-\omega t+\varphi )].}$$ ${\textstyle \cos a+\cos b=2\cos \left({a-b \over 2}\right)\cos \left({a+b \over 2}\right),}$ $${\displaystyle W_{1}+W_{2}=2A\cos \left({\varphi \over 2}\right)\cos \left(kx-\omega t+{\varphi \over 2}\right).}$$ ${\displaystyle \varphi /2}$

• Конструктивная интерференция : Если разность фаз четно кратна π : тогда , так что сумма двух волн представляет собой волну с удвоенной амплитудой ${\displaystyle \varphi =\ldots ,-4\pi ,-2\pi ,0,2\pi ,4\pi ,\ldots }$ ${\displaystyle \left|\cos(\varphi /2)\right|=1}$ $${\displaystyle W_{1}+W_{2}=2A\cos(kx-\omega t)}$$
• Деструктивная интерференция : Если разность фаз нечетно кратна π : тогда , поэтому сумма двух волн равна нулю. ${\displaystyle \varphi =\ldots ,-3\pi ,\,-\pi ,\,\pi ,\,3\pi ,\,5\pi ,\ldots }$ ${\displaystyle \cos(\varphi /2)=0\,}$ $${\displaystyle W_{1}+W_{2}=0}$$

Между двумя плоскими волнами

Геометрическое расположение для интерференции двух плоских волн

Интерференционные полосы в перекрывающихся плоских волнах

Простая форма интерференционной картины получается, если две плоские волны одинаковой частоты пересекаются под углом. Одна волна движется горизонтально, а другая движется вниз под углом θ к первой волне. Предполагая, что две волны находятся в фазе в точке B , относительная фаза изменяется вдоль оси x . Разность фаз в точке A определяется как

$${\displaystyle \Delta \varphi ={\frac {2\pi d}{\lambda }}={\frac {2\pi x\sin \theta }{\lambda }}.}$$

Видно, что две волны находятся в фазе, когда

$${\displaystyle {\frac {x\sin \theta }{\lambda }}=0,\pm 1,\pm 2,\ldots ,}$$

и находятся на полцикла в противофазе, когда

$${\displaystyle {\frac {x\sin \theta }{\lambda }}=\pm {\frac {1}{2}},\pm {\frac {3}{2}},\ldots }$$

Конструктивная интерференция происходит, когда волны находятся в фазе, а деструктивная интерференция — когда они находятся на полцикла в противофазе. Таким образом, получается интерференционная полоса, где разделение максимумов

$${\displaystyle d_{f}={\frac {\lambda }{\sin \theta }}}$$

и d _f известно как расстояние между полосами. Расстояние между полосами увеличивается с увеличением длины волны и уменьшением угла θ .

Полосы наблюдаются везде, где перекрываются две волны, а расстояние между полосами везде одинаковое.

Между двумя сферическими волнами

Оптическая интерференция между двумя точечными источниками, имеющими разные длины волн и расстояния между источниками.

Точечный источник создает сферическую волну. Если свет от двух точечных источников перекрывается, интерференционная картина отображает способ, которым разность фаз между двумя волнами изменяется в пространстве. Это зависит от длины волны и от разделения точечных источников. На рисунке справа показана интерференция двух сферических волн. Длина волны увеличивается сверху вниз, а расстояние между источниками увеличивается слева направо.

Когда плоскость наблюдения находится достаточно далеко, картина интерференции будет представлять собой ряд почти прямых линий, поскольку волны в этом случае будут почти плоскими.

Множественные лучи

Интерференция возникает при сложении нескольких волн при условии, что разность фаз между ними остается постоянной в течение времени наблюдения.

Иногда желательно, чтобы несколько волн одинаковой частоты и амплитуды суммировались до нуля (то есть, деструктивно интерферировали, гасили). Этот принцип лежит, например, в основе трехфазной мощности и дифракционной решетки . В обоих этих случаях результат достигается за счет равномерного расположения фаз.

Легко видеть, что набор волн будет гаситься, если они имеют одинаковую амплитуду и их фазы разнесены на одинаковый угол. Используя фазоры , каждую волну можно представить как для волн от до , где ${\displaystyle Ae^{i\varphi _{n}}}$ ${\displaystyle N}$ ${\displaystyle n=0}$ ${\displaystyle n=N-1}$ $${\displaystyle \varphi _{n}-\varphi _{n-1}={\frac {2\pi }{N}}.}$$

Чтобы показать, что $${\displaystyle \sum _{n=0}^{N-1}Ae^{i\varphi _{n}}=0}$$

просто предполагается обратное, затем обе стороны умножаются на ${\displaystyle e^{i{\frac {2\pi }{N}}}.}$

Интерферометр Фабри –Перо использует интерференцию многократных отражений.

Дифракционную решетку можно рассматривать как многолучевой интерферометр, поскольку пики, которые она создает, генерируются путем интерференции света, передаваемого каждым из элементов решетки; для дальнейшего обсуждения см. раздел интерференция и дифракция .

Комплекснозначные волновые функции

Механические и гравитационные волны можно наблюдать напрямую: они являются действительными волновыми функциями; оптические и материальные волны нельзя наблюдать напрямую: они являются комплексными волновыми функциями . Некоторые из различий между действительной и комплексной волновой интерференцией включают:

1. Интерференция включает в себя различные типы математических функций: Классическая волна — это действительная функция, представляющая смещение от положения равновесия; оптическая или квантовая волновая функция — это комплексная функция. Классическая волна в любой точке может быть положительной или отрицательной; квантовая функция вероятности неотрицательна.
2. Любые две различные реальные волны в одной и той же среде интерферируют; комплексные волны должны быть когерентными, чтобы интерферировать. На практике это означает, что волна должна исходить из одного источника и иметь схожие частоты
3. Реальная волновая интерференция получается простым сложением смещений от положения равновесия (или амплитуд) двух волн; при сложной волновой интерференции мы измеряем модуль волновой функции в квадрате.

Интерференция оптических волн

Создание интерференционных полос оптической плоскостью на отражающей поверхности. Световые лучи от монохроматического источника проходят через стекло и отражаются как от нижней поверхности плоскости, так и от опорной поверхности. Крошечный зазор между поверхностями означает, что два отраженных луча имеют разную длину пути. Кроме того, луч, отраженный от нижней пластины, претерпевает фазовый переворот на 180°. В результате в местах (a) , где разность хода является нечетным кратным λ/2, волны усиливаются. В местах (b) , где разность хода является четным кратным λ/2, волны гасятся. Поскольку зазор между поверхностями немного различается по ширине в разных точках, видны серии чередующихся светлых и темных полос, интерференционных полос .

Поскольку частота световых волн (~10 ¹⁴ Гц) слишком высока для имеющихся в настоящее время детекторов, чтобы обнаружить изменение электрического поля света, можно наблюдать только интенсивность оптической интерференционной картины. Интенсивность света в данной точке пропорциональна квадрату средней амплитуды волны. Это можно выразить математически следующим образом. Смещение двух волн в точке r равно:

$${\displaystyle U_{1}(\mathbf {r} ,t)=A_{1}(\mathbf {r} )e^{i[\varphi _{1}(\mathbf {r} )-\omega t]}}$$ $${\displaystyle U_{2}(\mathbf {r} ,t)=A_{2}(\mathbf {r} )e^{i[\varphi _{2}(\mathbf {r} )-\omega t]}}$$

где A представляет собой величину смещения, φ представляет собой фазу, а ω представляет собой угловую частоту .

Смещение суммарных волн равно

$${\displaystyle U(\mathbf {r} ,t)=A_{1}(\mathbf {r} )e^{i[\varphi _{1}(\mathbf {r} )-\omega t]}+A_{2}(\mathbf {r} )e^{i[\varphi _{2}(\mathbf {r} )-\omega t]}.}$$

Интенсивность света в точке r определяется выражением

$${\displaystyle I(\mathbf {r} )=\int U(\mathbf {r} ,t)U^{*}(\mathbf {r} ,t)\,dt\propto A_{1}^{2}(\mathbf {r} )+A_{2}^{2}(\mathbf {r} )+2A_{1}(\mathbf {r} )A_{2}(\mathbf {r} )\cos[\varphi _{1}(\mathbf {r} )-\varphi _{2}(\mathbf {r} )].}$$

Это можно выразить через интенсивности отдельных волн как

$${\displaystyle I(\mathbf {r} )=I_{1}(\mathbf {r} )+I_{2}(\mathbf {r} )+2{\sqrt {I_{1}(\mathbf {r} )I_{2}(\mathbf {r} )}}\cos[\varphi _{1}(\mathbf {r} )-\varphi _{2}(\mathbf {r} )].}$$

Таким образом, интерференционная картина отображает разницу фаз между двумя волнами, причем максимумы возникают, когда разность фаз кратна 2π . Если два луча имеют одинаковую интенсивность, то максимумы в четыре раза ярче отдельных лучей, а минимумы имеют нулевую интенсивность.

Классически две волны должны иметь одинаковую поляризацию , чтобы вызвать интерференционные полосы, поскольку волны с разной поляризацией не могут ни компенсировать друг друга, ни суммироваться. Вместо этого, когда волны с разной поляризацией складываются, они дают волну с другим состоянием поляризации .

Квантово-механические теории Поля Дирака и Ричарда Фейнмана предлагают более современный подход. Дирак показал, что каждый квант или фотон света действует сам по себе, что он знаменито сформулировал как «каждый фотон интерферирует сам с собой». Ричард Фейнман показал, что при оценке интеграла траектории, где рассматриваются все возможные пути, возникает ряд более вероятностных путей. Например, в тонких пленках толщина пленки, которая не кратна длине волны света, не позволит квантам пройти, возможно только отражение.

Требования к источнику света

Приведенное выше обсуждение предполагает, что интерферирующие друг с другом волны монохроматичны, т. е. имеют одну частоту — это требует, чтобы они были бесконечны во времени. Однако это непрактично и не необходимо. Две идентичные волны конечной длительности, частота которых фиксирована в течение этого периода, приведут к интерференционной картине, пока они перекрываются. Две идентичные волны, которые состоят из узкого спектра частотных волн конечной длительности (но короче, чем время их когерентности), дадут ряд картин полос со слегка различающимися интервалами, и при условии, что разброс интервалов значительно меньше среднего интервала между полосами, картина полос снова будет наблюдаться в то время, когда две волны перекрываются.

Обычные источники света излучают волны разной частоты и в разное время из разных точек источника. Если свет разделить на две волны, а затем снова объединить, каждая отдельная световая волна может генерировать интерференционную картину со своей другой половиной, но отдельные сгенерированные картины полос будут иметь разные фазы и интервалы, и обычно общая картина полос не будет наблюдаться. Однако одноэлементные источники света, такие как натриевые или ртутные лампы, имеют линии излучения с довольно узкими частотными спектрами. Когда они пространственно и цветно фильтруются, а затем разделяются на две волны, они могут быть наложены для генерации интерференционных полос. ^[5] Вся интерферометрия до изобретения лазера проводилась с использованием таких источников и имела широкий спектр успешных применений.

Лазерный луч обычно гораздо ближе приближается к монохроматическому источнику, и поэтому гораздо проще генерировать интерференционные полосы с помощью лазера. Легкость, с которой интерференционные полосы можно наблюдать с помощью лазерного луча, иногда может вызывать проблемы, поскольку случайные отражения могут давать ложные интерференционные полосы, которые могут приводить к ошибкам.

Обычно в интерферометрии используется один лазерный луч, хотя интерференция наблюдалась при использовании двух независимых лазеров, частоты которых были достаточно согласованы для удовлетворения фазовых требований. ^[6] Это также наблюдалось для широкопольной интерференции между двумя некогерентными лазерными источниками. ^[7]

Также возможно наблюдать интерференционные полосы с использованием белого света. Картина полос белого света может рассматриваться как состоящая из «спектра» картин полос, каждая из которых имеет немного разный интервал. Если все картины полос находятся в фазе в центре, то полосы будут увеличиваться в размере по мере уменьшения длины волны, а суммированная интенсивность покажет три-четыре полосы разного цвета. Янг описывает это очень элегантно в своем обсуждении двухщелевой интерференции. Поскольку полосы белого света получаются только тогда, когда две волны прошли равные расстояния от источника света, они могут быть очень полезны в интерферометрии, поскольку они позволяют идентифицировать полосу с нулевой разностью хода. ^[8]

Оптические устройства

Для генерации интерференционных полос свет от источника должен быть разделен на две волны, которые затем должны быть повторно объединены. Традиционно интерферометры классифицируются как системы с делением амплитуды или с делением волнового фронта.

В системе амплитудного деления светоделитель используется для разделения света на два луча, идущих в разных направлениях, которые затем накладываются друг на друга для создания интерференционной картины. Интерферометр Майкельсона и интерферометр Маха-Цендера являются примерами систем амплитудного деления.

В системах разделения волнового фронта волна разделяется в пространстве — примерами являются двухщелевой интерферометр Юнга и зеркало Ллойда .

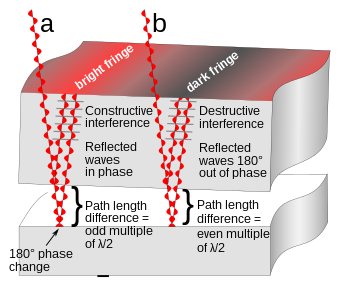
Интерференцию можно наблюдать и в повседневных явлениях, таких как иризация и структурная окраска . Например, цвета, которые мы видим в мыльном пузыре, возникают из-за интерференции света, отражающегося от передней и задней поверхностей тонкой мыльной пленки. В зависимости от толщины пленки разные цвета интерферируют конструктивно и деструктивно.

• Иридисценция, вызванная тонкопленочной интерференцией
• 
  Смартфон с переливающейся задней панелью
• 
  Разлив нефти
• 
  Интерференция белого света в мыльном пузыре.

Квантовая интерференция

Квантовая интерференция – наблюдаемое волновое поведение материи ^[9] – напоминает оптическую интерференцию. Пусть будет решением волновой функции уравнения Шредингера для квантово-механического объекта. Тогда вероятность наблюдения объекта в положении равна где * указывает на комплексное сопряжение . Квантовая интерференция касается вопроса этой вероятности, когда волновая функция выражается как сумма или линейная суперпозиция двух членов : ${\displaystyle \Psi (x,t)}$ ${\displaystyle P(x)}$ ${\displaystyle x}$ ${\displaystyle P(x)=|\Psi (x,t)|^{2}=\Psi ^{*}(x,t)\Psi (x,t)}$ ${\displaystyle \Psi (x,t)=\Psi _{A}(x,t)+\Psi _{B}(x,t)}$ $${\displaystyle P(x)=|\Psi (x,t)|^{2}=|\Psi _{A}(x,t)|^{2}+|\Psi _{B}(x,t)|^{2}+(\Psi _{A}^{*}(x,t)\Psi _{B}(x,t)+\Psi _{A}(x,t)\Psi _{B}^{*}(x,t))}$$

Обычно и соответствуют различным ситуациям A и B. В этом случае уравнение указывает, что объект может находиться в ситуации A или ситуации B. Приведенное выше уравнение можно интерпретировать следующим образом: Вероятность нахождения объекта в равна вероятности нахождения объекта в , когда он находится в ситуации A, плюс вероятность нахождения объекта в , когда он находится в ситуации B, плюс дополнительный член. Этот дополнительный член, который называется квантовым интерференционным членом , находится в приведенном выше уравнении. Как и в классическом волновом случае выше, квантовый интерференционный член может добавляться (конструктивная интерференция) или вычитаться (деструктивная интерференция) из в приведенном выше уравнении в зависимости от того, является ли квантовый интерференционный член положительным или отрицательным. Если этот член отсутствует для всех , то квантово-механической интерференции, связанной с ситуациями A и B, нет. ${\displaystyle \Psi _{A}(x,t)}$ ${\displaystyle \Psi _{B}(x,t)}$ ${\displaystyle \Psi (x,t)=\Psi _{A}(x,t)+\Psi _{B}(x,t)}$ ${\displaystyle x}$ ${\displaystyle x}$ ${\displaystyle x}$ ${\displaystyle \Psi _{A}^{*}(x,t)\Psi _{B}(x,t)+\Psi _{A}(x,t)\Psi _{B}^{*}(x,t)}$ ${\displaystyle |\Psi _{A}(x,t)|^{2}+|\Psi _{B}(x,t)|^{2}}$ ${\displaystyle x}$

Самым известным примером квантовой интерференции является эксперимент с двумя щелями . В этом эксперименте волны материи от электронов, атомов или молекул приближаются к барьеру с двумя щелями в нем. Одна щель становится , а другая становится . Картина интерференции возникает на дальней стороне, наблюдаемой детекторами, подходящими для частиц, порождающих волну материи . ^[10] Картина соответствует оптической картине с двумя щелями. ${\displaystyle \Psi _{A}(x,t)}$ ${\displaystyle \Psi _{B}(x,t)}$

Приложения

Бить

В акустике биение — это интерференционная картина двух звуков с немного разными частотами , воспринимаемая как периодическое изменение громкости , скорость которого равна разнице двух частот.

С помощью инструментов настройки , которые могут производить устойчивые тоны, биения можно легко распознать. Настройка двух тонов в унисон представит своеобразный эффект: когда два тона близки по высоте, но не идентичны, разница в частоте генерирует биения. Громкость меняется, как в тремоло , поскольку звуки попеременно мешают конструктивно и деструктивно. По мере того, как два тона постепенно приближаются к унисону, биения замедляются и могут стать настолько медленными, что станут незаметными. По мере того, как два тона отдаляются друг от друга, их частота биений начинает приближаться к диапазону человеческого восприятия высоты тона, ^[11] биения начинают звучать как нота, и получается комбинированный тон . Этот комбинированный тон также можно назвать отсутствующим основным тоном , поскольку частота биений любых двух тонов эквивалентна частоте их подразумеваемой основной частоты.

Оптическая интерферометрия

Интерферометрия сыграла важную роль в развитии физики, а также имеет широкий спектр применения в физических и инженерных измерениях.

Двухщелевой интерферометр Томаса Юнга в 1803 году продемонстрировал интерференционные полосы, когда два маленьких отверстия освещались светом из другого маленького отверстия, которое освещалось солнечным светом. Юнг смог оценить длину волны различных цветов в спектре по расстоянию между полосами. Эксперимент сыграл важную роль в общем принятии волновой теории света. ^[8] В квантовой механике этот эксперимент считается демонстрацией неразделимости волновой и корпускулярной природы света и других квантовых частиц ( корпускулярно-волновой дуализм ). Ричард Фейнман любил говорить, что вся квантовая механика может быть почерпнута из тщательного обдумывания последствий этого одного эксперимента. ^[12]

Результаты эксперимента Майкельсона–Морли обычно считаются первым весомым доказательством против теории светоносного эфира и в пользу специальной теории относительности .

Интерферометрия использовалась для определения и калибровки эталонов длины . Когда метр был определен как расстояние между двумя отметками на платиново-иридиевом стержне, Майкельсон и Бенуа использовали интерферометрию для измерения длины волны красной линии кадмия в новом стандарте, а также показали, что ее можно использовать в качестве эталона длины. Шестьдесят лет спустя, в 1960 году, метр в новой системе СИ был определен равным 1 650 763,73 длинам волн оранжево-красной линии излучения в электромагнитном спектре атома криптона-86 в вакууме. Это определение было заменено в 1983 году определением метра как расстояния, пройденного светом в вакууме за определенный промежуток времени. Интерферометрия по-прежнему является основополагающей в установлении калибровочной цепи при измерении длины.

Интерферометрия используется при калибровке скользящих калибров (в США их называют калибровочными блоками) и в координатно-измерительных машинах . Она также используется при тестировании оптических компонентов. ^[13]

Радиоинтерферометрия

Очень большая антенная решетка — интерферометрическая решетка , образованная из множества меньших телескопов , подобно множеству больших радиотелескопов .

В 1946 году была разработана техника, называемая астрономической интерферометрией . Астрономические радиоинтерферометры обычно состоят либо из массивов параболических тарелок, либо из двумерных массивов всенаправленных антенн. Все телескопы в массиве широко разнесены и обычно соединены вместе с помощью коаксиального кабеля , волновода , оптического волокна или другого типа линии передачи . Интерферометрия увеличивает общий собранный сигнал, но ее основная цель — значительно повысить разрешение с помощью процесса, называемого синтезом апертуры . Эта техника работает путем наложения (интерференции) волн сигнала от разных телескопов по принципу, что волны, совпадающие с одной и той же фазой, будут складываться друг с другом, в то время как две волны, имеющие противоположные фазы, будут нейтрализовать друг друга. Это создает комбинированный телескоп, который по разрешению (но не по чувствительности) эквивалентен одной антенне, диаметр которой равен расстоянию между антеннами, наиболее удаленными друг от друга в массиве.

Акустическая интерферометрия

Акустический интерферометр — это прибор для измерения физических характеристик звуковых волн в газе или жидкости, таких как скорость , длина волны, поглощение или импеданс . Вибрирующий кристалл создает ультразвуковые волны, которые излучаются в среду. Волны ударяются о рефлектор, расположенный параллельно кристаллу, отражаются обратно к источнику и измеряются.

Смотрите также

• Активный контроль шума
• Бит (акустика)
• Когерентность (физика)
• Дифракция
• бахрома Хайдингера
• Интерференционная литография
• Видимость помех
• Интерферометр
• Зеркало Ллойда
• Муаровый узор
• Многолучевые помехи
• Кольца Ньютона
• Длина оптического пути
• Интерференция тонкой пленки
• Критерий шероховатости Рэлея
• Upfade

Ссылки

1. О механизме глаза / Томас Янг.; Янг, Томас; Университетский колледж, Библиотечные службы Лондона (1801). Янг, Томас, 1773-1829. Университетский колледж Лондона (UCL) Библиотечные службы UCL. Лондон: напечатано W. Bulmer and Co., Cleveland Row, St. James's.
2. Джонс, Питер Уорд (2001). Издательство Оксфордского университета. Oxford Music Online. Издательство Оксфордского университета. doi :10.1093/gmo/9781561592630.article.20622.
3. Кипнис, Наум (1991). История принципа интерференции света. doi :10.1007/978-3-0348-8652-9. ISBN 978-3-0348-9717-4.
4. Окенга, Ваймке. Фазовый контраст. Leika Science Lab, 09 июня 2011 г. «Если две волны интерферируют, амплитуда результирующей световой волны будет равна векторной сумме амплитуд двух интерферирующих волн».
5. Steel, WH (1986). Интерферометрия . Кембридж: Cambridge University Press. ISBN 0-521-31162-4.
6. Пфлегор, Р. Л.; Мандель, Л. (1967). «Интерференция независимых фотонных пучков». Phys. Rev. 159 ( 5): 1084–1088. Bibcode :1967PhRv..159.1084P. doi :10.1103/physrev.159.1084.
7. Patel, R.; Achamfuo-Yeboah, S.; Light R.; Clark M. (2014). «Широкопольная двухлазерная интерферометрия». Optics Express . 22 (22): 27094–27101. Bibcode : 2014OExpr..2227094P. doi : 10.1364/OE.22.027094 . PMID  25401860.
8. Борн, Макс ; Вольф, Эмиль (1999). Принципы оптики . Кембридж: Издательство Кембриджского университета. ISBN 0-521-64222-1.
9. Фейнман Р. , Лейтон Р. и Сэндс М. , Сайт лекций Фейнмана, сентябрь 2013 г. «Лекции Фейнмана по физике, том III» (онлайн-издание)
10. Бах, Роджер; Поуп, Дамиан; Лиу, Си-Хванг; Бателан, Герман (2013-03-13). "Управляемая двухщелевая электронная дифракция". New Journal of Physics . 15 (3). IOP Publishing: 033018. arXiv : 1210.6243 . doi : 10.1088/1367-2630/15/3/033018. ISSN  1367-2630. S2CID  832961.
11. Левитин, Дэниел Дж. (2006). Это ваш мозг в музыке: наука о человеческой одержимости . Даттон. стр. 22. ISBN 978-0525949695.
12. Грин, Брайан (1999). Элегантная Вселенная: Суперструны, Скрытые Измерения и Поиски Окончательной Теории . Нью-Йорк: WW Norton. С. 97–109. ISBN 978-0-393-04688-5.
13. RS Longhurst, Геометрическая и физическая оптика , 1968, Longmans, Лондон.

Внешние ссылки

• Простая имитационная модель одномерной интерференции волн на JavaScript
• Выражения положения и расстояния между полосами
• Моделирование интерференции волн на воде на Java 1
• Моделирование интерференции волн на воде на Java 2
• Флэш-анимация, демонстрирующая интерференцию. Архивировано 24.06.2009 на Wayback Machine.