Закон квадрата-куба

Связь между площадью поверхности и объемом по мере увеличения размера

Закон квадрата-куба впервые упоминается в книге «Две новые науки» (1638 г.).

Закон квадрата-куба (или закон куба-квадрата ) — это математический принцип, применяемый в различных научных областях, который описывает взаимосвязь между объемом и площадью поверхности по мере увеличения или уменьшения размера формы. Впервые это было ^{[ сомнительно ]} описано в 1638 году Галилео Галилеем в его «Двух новых науках» как «…отношение двух объёмов больше, чем соотношение их поверхностей». ^[1]

Этот принцип гласит, что по мере увеличения размера формы ее объем растет быстрее, чем площадь поверхности. Применительно к реальному миру этот принцип имеет множество последствий, которые важны в самых разных областях: от машиностроения до биомеханики . Это помогает объяснить такие явления, как, например, почему крупным млекопитающим, таким как слоны, труднее охлаждаться, чем маленьким, таким как мыши, и почему строить все более высокие небоскребы становится все труднее.

Описание

Графики зависимости площади поверхности A от объема V платоновых тел и сферы, показывающие, что отношение площади поверхности к объему уменьшается с увеличением объема.
Пунктирные стрелки показывают, что при увеличении объема в 8 (2³) раз площадь поверхности увеличивается в 4 (2²) раза.

Эта картина проясняет взаимосвязь между длиной стороны многогранника, площадью его поверхности и объемом.

Закон квадрата-куба можно сформулировать следующим образом:

Когда объект пропорционально увеличивается в размерах, его новая площадь поверхности пропорциональна квадрату множителя, а его новый объем пропорционален кубу множителя.

Представлено математически: ^[2]

$${\displaystyle A_{2}=A_{1}\left({\frac {\ell _{2}}{\ell _{1}}}\right)^{2}}$$

${\displaystyle A_{1}}$ ${\displaystyle A_{2}}$

$${\displaystyle V_{2}=V_{1}\left({\frac {\ell _{2}}{\ell _{1}}}\right)^{3}}$$

${\displaystyle V_{1}}$ ${\displaystyle V_{2}}$ ${\displaystyle \ell _{1}}$ ${\displaystyle \ell _{2}}$

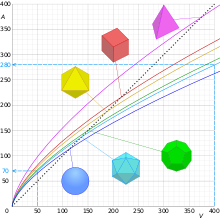
Например, куб со стороной 1 метр имеет площадь поверхности 6 м ² и объем 1 м ³ . Если стороны куба умножить на 2, площадь его поверхности умножится на квадрат 2 и составит 24 м ² . Его объем умножили бы на куб 2 и составили бы 8 м ³ .

Исходный куб (сторона 1 м) имеет соотношение площади поверхности к объему 6:1. Куб большего размера (стороны 2 м) имеет соотношение площади поверхности к объему (24/8) 3:1. По мере увеличения размеров объем будет продолжать расти быстрее, чем площадь поверхности. Отсюда закон квадрата-куба. Этот принцип применим ко всем твердым телам. ^[3]

Приложения

Инженерное дело

Когда физический объект сохраняет ту же плотность и масштабируется, его объем и масса увеличиваются на куб множителя, а площадь его поверхности увеличивается только на квадрат того же множителя. Это будет означать, что когда большая версия объекта ускоряется с той же скоростью, что и исходная, на поверхность большего объекта будет оказываться большее давление.

Рассмотрим простой пример тела массы , испытывающего ускорение , с площадью поверхности , на которую действует ускоряющая сила . Сила, возникающая вследствие ускорения, равна , а давление равно . ${\displaystyle m}$ ${\displaystyle a}$ ${\displaystyle A}$ ${\displaystyle F=ma}$ ${\displaystyle P={\frac {F}{A}}={\frac {ma}{A}}}$

Теперь предположим, что объект увеличен с помощью множителя, так что он имеет новую массу и новую площадь поверхности . ${\displaystyle x}$ ${\displaystyle m'=x^{3}m}$ ${\displaystyle A'=x^{2}A}$

Новая сила, возникающая вследствие ускорения, равна результирующему давлению: ${\displaystyle F'=x^{3}ma}$

$${\displaystyle {\begin{aligned}P'&={\frac {F'}{A'}}\\&={\frac {x^{3}ma}{x^{2}A}}\\&=x\ {\frac {ma}{A}}\\&=x\ P\\\end{aligned}}}$$

Таким образом, простое увеличение размера объекта при сохранении того же материала конструкции (плотности) и того же ускорения приведет к увеличению давления на тот же коэффициент масштабирования. Это будет указывать на то, что объект будет иметь меньшую способность противостоять стрессу и будет более склонен к разрушению при ускорении.

Вот почему большие автомобили плохо справляются с краш-тестами и почему существуют теоретические ограничения на возведение высоких зданий. Аналогичным образом, чем больше объект, тем меньше другие объекты будут сопротивляться его движению, вызывая его замедление.

Инженерные примеры

• Паровой двигатель : Джеймсу Уотту , работавшему приборостроителем в Университете Глазго , была предоставлена ​​масштабная модель парового двигателя Ньюкомена, чтобы привести его в рабочее состояние. Ватт понял, что проблема связана с законом квадрата-куба, заключающимся в том, что отношение поверхности к объему цилиндра модели было больше, чем у гораздо более крупных коммерческих двигателей, что приводило к чрезмерным потерям тепла. ^[4] Эксперименты с этой моделью привели к знаменитым усовершенствованиям Уатта парового двигателя.

Боинг 737-500 перед Airbus A380

• Airbus A380 : подъемная сила и поверхности управления (крылья, рули направления и рули высоты) относительно большие по сравнению с фюзеляжем самолета. Например, если взять Боинг 737 и просто увеличить его размеры до размеров А380, то крылья станут слишком маленькими для веса самолета из-за правила квадрата-куба.
• Ракетные двигатели с детандерным циклом страдают от закона квадрата-куба. Их размер и, следовательно, тяга ограничены эффективностью теплопередачи, поскольку площадь поверхности сопла увеличивается медленнее, чем объем топлива, протекающего через сопло.
• Клиперу требуется относительно большая поверхность паруса, чем шлюпу , чтобы достичь той же скорости, а это означает , что между этими судами соотношение площади паруса к поверхности паруса выше, чем соотношение веса к весу.
• Аэростаты обычно выигрывают от закона квадрата-куба. По мере увеличения радиуса ( ) ${\displaystyle r^{1}}$ воздушного шара стоимость площади поверхности увеличивается в квадрате ( ) ${\displaystyle r^{2}}$ , но подъемная сила, создаваемая объемом, увеличивается в кубическом масштабе ( ) ${\displaystyle r^{3}}$ .
• Структурное проектирование : материалы, которые работают в небольших масштабах, могут не работать в больших масштабах. Например, сжимающее напряжение внизу небольшой отдельно стоящей колонны масштабируется с той же скоростью, что и размер колонны. Следовательно, для данного материала и плотности существует размер, при котором колонна рухнет сама на себя.

Биомеханика

Если бы животное было изометрически увеличено на значительную величину, его относительная мышечная сила была бы сильно уменьшена, поскольку поперечное сечение его мышц увеличилось бы в квадрате масштабного коэффициента, а его масса увеличилась бы в кубе масштабного коэффициента. . В результате этого сердечно-сосудистые и дыхательные функции будут сильно отягощены.

В случае летающих животных нагрузка на крылья была бы увеличена, если бы они были изометрически увеличены, и поэтому им пришлось бы летать быстрее, чтобы получить ту же подъемную силу . Сопротивление воздуха на единицу массы также выше для более мелких животных (снижается конечная скорость ), поэтому такое маленькое животное, как муравей, не может получить серьезные травмы от удара о землю после падения с любой высоты.

Как заявил Дж.Б.С. Холдейн , крупные животные не похожи на мелких: слона нельзя спутать с увеличенной в размерах мышью. Это связано с аллометрическим масштабированием : кости слона обязательно пропорционально намного больше, чем кости мыши, потому что они должны нести пропорционально больший вес. Холдейн иллюстрирует это в своем основополагающем эссе 1928 года «Быть ​​правильным размером», обращаясь к аллегорическим гигантам: «...представьте себе человека ростом 60 футов... Гигантский Папа и Гигантский язычник в иллюстрированном « Путешествии пилигрима»: ...Эти монстры... .весил в 1000 раз больше, чем [нормальный человек]. Каждый квадратный дюйм гигантской кости должен был выдерживать вес, в 10 раз превышающий вес, выдерживаемый квадратным дюймом человеческой кости, поскольку бедренная кость среднего человека ломается примерно в 10 раз больше, чем у человека. веса, Поуп и Пэган сломали бы себе бедра каждый раз, когда бы сделали шаг». ^[5] Следовательно, у большинства животных наблюдается аллометрическое масштабирование с увеличением размера как между видами, так и внутри вида. Гигантские существа, которые можно увидеть в фильмах о монстрах (например, «Годзилла» , «Кинг-Конг» , «Они!» и другие кайдзю ), также нереалистичны, учитывая, что их огромный размер заставил бы их рухнуть.

Однако плавучесть воды в некоторой степени сводит на нет действие гравитации. Следовательно, водные животные могут вырасти до очень больших размеров, не имея тех же скелетно-мышечных структур, которые необходимы наземным животным аналогичного размера, и это основная причина того, что самые большие животные, когда-либо существовавшие на Земле, являются водными животными .

Скорость метаболизма животных масштабируется с помощью математического принципа, называемого четвертьстепенным масштабированием ^[6] в соответствии с метаболической теорией экологии .

Массо- и теплопередача

Перенос массы, такой как диффузия к более мелким объектам, таким как живые клетки, происходит быстрее, чем диффузия к более крупным объектам, таким как целые животные. Таким образом, в химических процессах, протекающих на поверхности, а не в объеме, более активен более мелкодисперсный материал. Например, активность гетерогенного катализатора выше, если он разделен на более мелкие частицы. Такие катализаторы обычно встречаются в более теплых условиях.

Производство тепла в результате химического процесса масштабируется пропорционально кубу линейного размера (высоты, ширины) сосуда, но площадь поверхности сосуда масштабируется только квадрату линейного размера. Следовательно, более крупные сосуды гораздо труднее охладить. Кроме того, крупномасштабные трубопроводы для передачи горячих жидкостей трудно смоделировать в небольших масштабах, поскольку тепло передается быстрее из труб меньшего размера. Неспособность принять это во внимание при проектировании процесса может привести к катастрофическому тепловому разгону .

Смотрите также

• Биомеханика
• Аллометрический закон
• О том, как быть правильным размером , эссе Дж. Б. С. Холдейна , в котором рассматриваются изменения в форме животных, которые потребуются при значительном изменении размера. Также см. выше пример аллегорических гигантов при масштабировании размера.
• Отношение площади поверхности к объему
• Закон Клейбера
• Правило Бергмана

Рекомендации

1. Дэвид Х. Аллен (24 сентября 2013 г.). Как механика сформировала современный мир. Спрингер. ISBN 9783319017013. {{cite book}}: |work=игнорируется ( помощь )
2. «Строители мира: размеры живых существ». world-builders.org . Архивировано из оригинала 23 октября 2016 г. Проверено 21 апреля 2012 г.
3. Майкл К. Лабарбера. «Биология монстров из фильмов категории B».
4. Розен, Уильям (2012). Самая мощная идея в мире: история пара, промышленности и изобретений . Издательство Чикагского университета. п. 98. ИСБН 978-0226726342.
5. Холдейн, JBS «О правильном размере». Лаборатория интернет-исследований. Калифорнийский университет в Лос-Анджелесе. Архивировано из оригинала 22 августа 2011 года . Проверено 1 апреля 2017 г.
6. Джордж Джонсон (12 января 1999 г.). «О мышах и слонах: вопрос масштаба». Нью-Йорк Таймс . Проверено 11 июня 2015 г.

Внешние ссылки

• Учебные материалы по пропорциям в Викиверситете