конический Штейнер

1. Определение генерации Штейнера конического сечения

Коническое сечение Штейнера или, точнее, генерация конического сечения Штейнера , названная в честь швейцарского математика Якоба Штейнера , является альтернативным методом определения невырожденного проективного конического сечения в проективной плоскости над полем .

Обычное определение конического сечения использует квадратичную форму (см. Квадрика (проективная геометрия) ). Другое альтернативное определение конического сечения использует гиперболическую полярность . Оно принадлежит КГК фон Штаудта и иногда называется коническим сечением фон Штаудта . Недостатком определения фон Штаудта является то, что оно работает только тогда, когда базовое поле имеет нечетную характеристику (т. е. ). ${\displaystyle Char\neq 2}$

Определение коники Штейнера

• Даны два пучка прямых в двух точках (все прямые содержат и соответственно) и проективное, но не перспективное отображение на . Тогда точки пересечения соответствующих прямых образуют невырожденное проективное коническое сечение ^{[1] [2] [3] [4]} ( рисунок 1) ${\displaystyle B(U),B(V)}$ ${\displaystyle U,V}$ ${\displaystyle U}$ ${\displaystyle V}$ ${\displaystyle \pi }$ ${\displaystyle B(U)}$ ${\displaystyle B(V)}$

2. Перспективное отображение между линиями

Перспективное отображение карандаша на карандаш представляет собой биекцию (соответствие 1-1), при котором соответствующие прямые пересекаются на фиксированной прямой , которая называется осью перспективы (рисунок 2). ${\displaystyle \pi }$ ${\displaystyle B(U)}$ ${\displaystyle B(V)}$ ${\displaystyle a}$ ${\displaystyle \pi }$

Проективное отображение — это конечное произведение перспективных отображений .

Простой пример: Если сдвинуть на первой диаграмме точку и ее пучок линий на и повернуть сдвинутый карандаш вокруг на фиксированный угол , то сдвиг (трансляция) и поворот порождают проективное отображение пучка в точке на пучок в . Из теоремы о вписанном угле получаем: Точки пересечения соответствующих линий образуют окружность. ${\displaystyle U}$ ${\displaystyle V}$ ${\displaystyle V}$ ${\displaystyle \varphi }$ ${\displaystyle \pi }$ ${\displaystyle U}$ ${\displaystyle V}$

Примерами часто используемых полей являются действительные числа , рациональные числа или комплексные числа . Конструкция также работает над конечными полями, предоставляя примеры в конечных проективных плоскостях . ${\displaystyle \mathbb {R} }$ ${\displaystyle \mathbb {Q} }$ ${\displaystyle \mathbb {C} }$

Замечание: Основная теорема для проективных плоскостей утверждает ^[5] , что проективное отображение в проективной плоскости над полем ( папповой плоскости ) однозначно определяется заданием образов трех прямых. Это означает, что для генерации Штейнера конического сечения, помимо двух точек, должны быть заданы только образы трех прямых. Эти 5 элементов (2 точки, 3 прямые) однозначно определяют коническое сечение. ${\displaystyle U,V}$

Замечание: Обозначение «перспектива» обусловлено двойственным утверждением: проекция точек на прямой из центра на прямую называется перспективой (см. ниже). ^[5] ${\displaystyle a}$ ${\displaystyle Z}$ ${\displaystyle b}$

3. Пример генерации Штейнера: генерация точки

Пример

Для следующего примера даны изображения прямых (см. рисунок): . Проективное отображение является произведением следующих перспективных отображений : 1) - перспективное отображение карандаша в точке на карандаш в точке с осью . 2) - перспективное отображение карандаша в точке на карандаш в точке с осью . Сначала следует проверить, что имеет свойства: . Следовательно, для любой прямой можно построить изображение и, следовательно, изображения произвольного набора точек. Прямые и содержат только конические точки и соответственно.. Следовательно , и являются касательными линиями порожденного конического сечения. ${\displaystyle a,u,w}$ ${\displaystyle \pi (a)=b,\pi (u)=w,\pi (w)=v}$ ${\displaystyle \pi }$ ${\displaystyle \pi _{b},\pi _{a}}$ ${\displaystyle \pi _{b}}$ ${\displaystyle U}$ ${\displaystyle O}$ ${\displaystyle b}$ ${\displaystyle \pi _{a}}$ ${\displaystyle O}$ ${\displaystyle V}$ ${\displaystyle a}$ ${\displaystyle \pi =\pi _{a}\pi _{b}}$ ${\displaystyle \pi (a)=b,\pi (u)=w,\pi (w)=v}$ ${\displaystyle g}$ ${\displaystyle \pi (g)=\pi _{a}\pi _{b}(g)}$ ${\displaystyle u}$ ${\displaystyle v}$ ${\displaystyle U}$ ${\displaystyle V}$ ${\displaystyle u}$ ${\displaystyle v}$

Доказательство того, что этот метод генерирует коническое сечение , следует из перехода к аффинному ограничению с прямой как линией на бесконечности , точкой как началом системы координат с точками как точками на бесконечности осей x и y соответственно и точкой . Аффинная часть сгенерированной кривой, по-видимому, является гиперболой . [ ^2] ${\displaystyle w}$ ${\displaystyle O}$ ${\displaystyle U,V}$ ${\displaystyle E=(1,1)}$ ${\displaystyle y=1/x}$

Замечание:

1. Метод Штейнера для конического сечения обеспечивает простые методы построения эллипсов , парабол и гипербол, которые обычно называют методами параллелограмма .
2. Фигура, которая появляется при построении точки (рисунок 3), представляет собой 4-точечное вырождение теоремы Паскаля . ^[6]

Генерация Штейнера двойной коники

двойной эллипс

Генерация Штейнера двойной коники

определение перспективного отображения

Определения и двойное поколение

Дуализация (см. двойственность (проективная геометрия) ) проективной плоскости означает замену точек прямыми и операции пересечения и соединения . Двойственная структура проективной плоскости также является проективной плоскостью. Двойственная плоскость папповской плоскости является папповской и также может быть координирована однородными координатами. Невырожденное двойственное коническое сечение аналогично определяется квадратичной формой.

Двойственную конику можно получить с помощью двойственного метода Штейнера:

• Даны множества точек двух прямых и проективное, но не перспективное отображение на . Тогда прямые , соединяющие соответствующие точки, образуют двойственное невырожденное проективное коническое сечение. ${\displaystyle u,v}$ ${\displaystyle \pi }$ ${\displaystyle u}$ ${\displaystyle v}$

Перспективное отображение множества точек прямой на множество точек прямой — это биекция (соответствие 1-1), при котором соединяющие линии соответствующих точек пересекаются в фиксированной точке , которая называется центром перспективы (см. рисунок). ${\displaystyle \pi }$ ${\displaystyle u}$ ${\displaystyle v}$ ${\displaystyle Z}$ ${\displaystyle \pi }$

Проективное отображение — это конечная последовательность перспективных отображений.

Принято, когда речь идет о двойственных и общих конических сечениях, называть общее коническое сечение точечной коникой , а двойственную конику — прямой коникой .

В случае, если в основном поле все касательные точечной коники пересекаются в точке, называемой узлом (или ядром ) коники. Таким образом, двойственная к невырожденной точечной конике является подмножеством точек двойственной прямой, а не овальной кривой (в двойственной плоскости). Таким образом, только в случае, когда двойственная к невырожденной точечной конике является невырожденной прямой коникой. ${\displaystyle \operatorname {Char} =2}$ ${\displaystyle \operatorname {Char} \neq 2}$

Примеры

Двойная коника Штейнера, определяемая двумя перспективами ${\displaystyle \pi _{A},\pi _{B}}$

пример генерации Штейнера двойственной коники

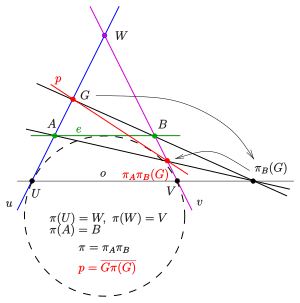
(1) Проективность, заданная двумя перспективами: Даны
две прямые с точкой пересечения и проективность из на двумя перспективами с центрами . отображает линию на третью линию , отображает линию на линию (см. диаграмму). Точка не должна лежать на линиях . Проективность является композицией двух перспектив: . Следовательно, точка отображается на , а линия является элементом двойственной коники, определяемой . (Если бы была фиксированной точкой, была бы перспективой. ^[7] ) ${\displaystyle u,v}$ ${\displaystyle W}$ ${\displaystyle \pi }$ ${\displaystyle u}$ ${\displaystyle v}$ ${\displaystyle \pi _{A},\pi _{B}}$ ${\displaystyle A,B}$ ${\displaystyle \pi _{A}}$ ${\displaystyle u}$ ${\displaystyle o}$ ${\displaystyle \pi _{B}}$ ${\displaystyle o}$ ${\displaystyle v}$ ${\displaystyle W}$ ${\displaystyle {\overline {AB}},o}$ ${\displaystyle \pi }$ ${\displaystyle \ \pi =\pi _{B}\pi _{A}}$ ${\displaystyle X}$ ${\displaystyle \pi (X)=\pi _{B}\pi _{A}(X)}$ ${\displaystyle x={\overline {X\pi (X)}}}$ ${\displaystyle \pi }$
${\displaystyle W}$ ${\displaystyle \pi }$

(2) Даны три точки и их образы:
Следующий пример является двойственным приведенному выше для коники Штейнера. Даны
образы точек : . Проективное отображение может быть представлено произведением следующих перспектив : ${\displaystyle A,U,W}$ ${\displaystyle \pi (A)=B,\,\pi (U)=W,\,\pi (W)=V}$ ${\displaystyle \pi }$ ${\displaystyle \pi _{B},\pi _{A}}$

1. ${\displaystyle \pi _{B}}$— это перспективность множества точек прямой на множество точек прямой с центром . ${\displaystyle u}$ ${\displaystyle o}$ ${\displaystyle B}$
2. ${\displaystyle \pi _{A}}$— это перспективность множества точек прямой на множество точек прямой с центром . ${\displaystyle o}$ ${\displaystyle v}$ ${\displaystyle A}$

Легко проверить, что проективное отображение удовлетворяет . Следовательно, для любой произвольной точки можно построить изображение , а прямая является элементом невырожденного двойственного конического сечения. Поскольку точки и содержатся в прямых , соответственно, точки и являются точками конического сечения, а прямые являются касательными в . ${\displaystyle \pi =\pi _{A}\pi _{B}}$ ${\displaystyle \pi (A)=B,\,\pi (U)=W,\,\pi (W)=V}$ ${\displaystyle G}$ ${\displaystyle \pi (G)=\pi _{A}\pi _{B}(G)}$ ${\displaystyle {\overline {G\pi (G)}}}$ ${\displaystyle U}$ ${\displaystyle V}$ ${\displaystyle u}$ ${\displaystyle v}$ ${\displaystyle U}$ ${\displaystyle V}$ ${\displaystyle u,v}$ ${\displaystyle U,V}$

Внутренние коники в линейной геометрии падения

Конструкция Штейнера определяет коники в плоской линейной геометрии инцидентности (две точки определяют не более одной прямой, а две прямые пересекаются не более чем в одной точке) внутренне , то есть, используя только группу коллинеаций. В частности, является коникой в ​​точке , полученной коллинеацией , состоящей из пересечений и для всех прямых, проходящих через . Если или для некоторых , то коника вырождена . Например, в действительной координатной плоскости аффинный тип (эллипс, парабола, гипербола) определяется следом и определителем матричной компоненты , независимой от . ${\displaystyle E(T,P)}$ ${\displaystyle P}$ ${\displaystyle T}$ ${\displaystyle L}$ ${\displaystyle T(L)}$ ${\displaystyle L}$ ${\displaystyle P}$ ${\displaystyle T(P)=P}$ ${\displaystyle T(L)=L}$ ${\displaystyle L}$ ${\displaystyle E(T,P)}$ ${\displaystyle T}$ ${\displaystyle P}$

Напротив, группа коллинеаций действительной гиперболической плоскости состоит из изометрий. Следовательно, внутренние коники включают небольшое, но разнообразное подмножество общих коник , кривых, полученных из пересечений проективных коник с гиперболической областью. Кроме того, в отличие от евклидовой плоскости, нет перекрытия между прямой сохраняющей ориентацию – и противоположной обратящей ориентацией. Прямой случай включает центральные (две перпендикулярные линии симметрии) и нецентральные коники, тогда как каждая противоположная коника является центральной. Несмотря на то, что прямая и противоположная центральная коники не могут быть конгруэнтными, они связаны квазисимметрией, определяемой в терминах дополнительных углов параллельности. Таким образом, в любой инверсной модели каждая прямая центральная коника бирационально эквивалентна противоположной центральной конике. ^[8] Фактически, центральные коники представляют все кривые рода 1 с действительной инвариантной формой . Минимальный набор представителей получается из центральных прямых коник с общим центром и осью симметрии, при этом инвариант формы является функцией эксцентриситета , определяемого в терминах расстояния между и . Ортогональные траектории этих кривых представляют все кривые рода 1 с , которые проявляются либо как неприводимые кубики, либо как бикруговые квартики. Используя закон сложения эллиптических кривых на каждой траектории, каждая общая центральная коника в разлагается однозначно как сумма двух внутренних коник путем добавления пар точек, где коники пересекают каждую траекторию. ^[9] ${\displaystyle \mathbb {H} ^{2}}$ ${\displaystyle E(T,P);}$ ${\displaystyle T}$ ${\displaystyle E(T,P);}$ ${\displaystyle T}$ ${\displaystyle \mathbb {H} ^{2}}$ ${\displaystyle j\geq 1}$ ${\displaystyle P}$ ${\displaystyle T(P)}$ ${\displaystyle j\leq 1}$ ${\displaystyle \mathbb {H} ^{2}}$

Примечания

1. Коксетер 1993, стр. 80
2. Hartmann, стр. 38
3. Мерсерв 1983, стр. 65
4. Vorlesungen über Synthetische Geometrie Якоба Штайнера , Б. Г. Тойбнер, Лейпциг, 1867 г. (из Google Книги: (немецкий) Часть II следует за Частью I), Часть II, стр. 96
5. Hartmann, стр. 19
6. Хартманн, стр. 32
7. Х. Ленц: Vorlesungen über projemetrie , BI, Мангейм, 1965, S. 49.
8. Сарли, Джон (апрель 2012 г.). «Конические сечения в гиперболической плоскости, присущие группе коллинеаций». Журнал геометрии . 103 (1): 131–148. doi :10.1007/s00022-012-0115-5. ISSN  0047-2468. S2CID  119588289.
9. Сарли, Джон (2021-10-22). «Эллиптическая кривая разложения центральных коник в реальной гиперболической плоскости» (Препринт). doi :10.21203/rs.3.rs-936116/v1.

Ссылки

• Коксетер, HSM (1993), Реальная проективная плоскость , Springer Science & Business Media
• Хартманн, Эрих, Плоская круговая геометрия, введение в плоскости Мёбиуса, Лагерра и Минковского (PDF) , получено 20 сентября 2014 г.(PDF; 891 кБ).
• Мерсерв, Брюс Э. (1983) [1959], Основные понятия геометрии , Довер, ISBN 0-486-63415-9