Предел (теория категорий)

Математическая концепция

В теории категорий , разделе математики , абстрактное понятие предела охватывает существенные свойства универсальных конструкций , таких как произведения , обратные отступы и обратные пределы . Двойственное понятие копредела обобщает конструкции , такие как непересекающиеся объединения , прямые суммы , копроизведения , выталкивания и прямые пределы .

Пределы и копределы, как и тесно связанные понятия универсальных свойств и сопряженных функторов , существуют на высоком уровне абстракции. Чтобы понять их, полезно сначала изучить конкретные примеры, которые эти концепции призваны обобщать.

Определение

Пределы и копределы в категории определяются с помощью диаграмм в . Формально диаграмма формы в является функтором из в : ${\displaystyle C}$ ${\displaystyle C}$ ${\displaystyle J}$ ${\displaystyle C}$ ${\displaystyle J}$ ${\displaystyle C}$

${\displaystyle F:J\to C.}$

Категория рассматривается как индексная категория , а диаграмма рассматривается как индексация коллекции объектов и морфизмов , сформированных по образцу . ${\displaystyle J}$ ${\displaystyle F}$ ${\displaystyle C}$ ${\displaystyle J}$

Чаще всего интерес представляет случай, когда категория является малой или даже конечной категорией. Диаграмма считается малой или конечной всякий раз, когда это так. ${\displaystyle J}$ ${\displaystyle J}$

Пределы

Пусть будет диаграммой формы в категории . Конус в является объектом вместе с семейством морфизмов, индексированных объектами , таким образом, что для каждого морфизма в , мы имеем . ${\displaystyle F:J\to C}$ ${\displaystyle J}$ ${\displaystyle C}$ ${\displaystyle F}$ ${\displaystyle N}$ ${\displaystyle C}$ ${\displaystyle \psi _{X}:N\to F(X)}$ ${\displaystyle X}$ ${\displaystyle J}$ ${\displaystyle f:X\to Y}$ ${\displaystyle J}$ ${\displaystyle F(f)\circ \psi _{X}=\psi _{Y}}$

Пределом диаграммы является конус к , такой что для каждого конуса к существует единственный морфизм, такой что для всех в . ${\displaystyle F:J\to C}$ ${\displaystyle (L,\phi )}$ ${\displaystyle F}$ ${\displaystyle (N,\psi )}$ ${\displaystyle F}$ ${\displaystyle u:N\to L}$ ${\displaystyle \phi _{X}\circ u=\psi _{X}}$ ${\displaystyle X}$ ${\displaystyle J}$

Универсальный конус

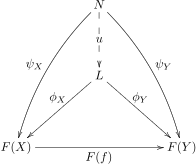
Говорят, что конус факторизуется через конус с уникальной факторизацией . Морфизм иногда называют опосредующим морфизмом . ${\displaystyle (N,\psi )}$ ${\displaystyle (L,\phi )}$ ${\displaystyle u}$ ${\displaystyle u}$

Пределы также называются универсальными конусами , поскольку они характеризуются универсальным свойством (см. ниже для получения дополнительной информации). Как и в случае с каждым универсальным свойством, приведенное выше определение описывает сбалансированное состояние общности: предельный объект должен быть достаточно общим, чтобы позволить любому конусу факторизоваться через него; с другой стороны, должен быть достаточно конкретным, чтобы для каждого конуса была возможна только одна такая факторизация. ${\displaystyle L}$ ${\displaystyle L}$

Пределы также могут быть охарактеризованы как конечные объекты в категории конусов F.

Возможно, что диаграмма вообще не имеет предела. Однако, если диаграмма имеет предел, то этот предел по сути уникален: он уникален с точностью до единственного изоморфизма . По этой причине часто говорят о пределе F .

Coпределы

Двойственные понятия пределов и конусов — это копределы и коконы. Хотя их определения легко получить, инвертируя все морфизмы в приведенных выше определениях, мы явно сформулируем их здесь:

Коконус диаграммы — это объект вместе с семейством морфизмов ${\displaystyle F:J\to C}$ ${\displaystyle N}$ ${\displaystyle C}$

${\displaystyle \psi _{X}:F(X)\to N}$

для каждого объекта из , такого, что для каждого морфизма из , мы имеем . ${\displaystyle X}$ ${\displaystyle J}$ ${\displaystyle f:X\to Y}$ ${\displaystyle J}$ ${\displaystyle \psi _{Y}\circ F(f)=\psi _{X}}$

Колимп диаграммы — это коконус , такой что для любого другого коконуса существует единственный морфизм такой, что для всех из . ${\displaystyle F:J\to C}$ ${\displaystyle (L,\phi )}$ ${\displaystyle F}$ ${\displaystyle (N,\psi )}$ ${\displaystyle F}$ ${\displaystyle u:L\to N}$ ${\displaystyle u\circ \phi _{X}=\psi _{X}}$ ${\displaystyle X}$ ${\displaystyle J}$

Универсальный ко-конус

Копределы также называются универсальными коконусами . Их можно охарактеризовать как начальные объекты в категории коконусов из . ${\displaystyle F}$

Как и в случае с пределами, если диаграмма имеет копредел, то этот копредел единственен с точностью до единственного изоморфизма. ${\displaystyle F}$

Вариации

Пределы и копределы также могут быть определены для коллекций объектов и морфизмов без использования диаграмм. Определения те же самые (обратите внимание, что в определениях выше нам никогда не нужно было использовать композицию морфизмов в ). Однако эта вариация не добавляет никакой новой информации. Любая коллекция объектов и морфизмов определяет (возможно, большой) ориентированный граф . Если мы позволим быть свободной категорией , сгенерированной , то существует универсальная диаграмма, изображение которой содержит . Предел (или копредел) этой диаграммы такой же, как предел (или копредел) исходной коллекции объектов и морфизмов. ${\displaystyle J}$ ${\displaystyle G}$ ${\displaystyle J}$ ${\displaystyle G}$ ${\displaystyle F:J\to C}$ ${\displaystyle G}$

Слабый предел и слабые копределы определяются так же, как пределы и копределы, за исключением того, что свойство уникальности опосредующего морфизма отбрасывается.

Примеры

Пределы

Определение пределов достаточно общее , чтобы включить несколько конструкций, полезных в практических условиях. Далее мы рассмотрим предел ( L , φ ) диаграммы F  : J → C.

• Терминальные объекты . Если J — пустая категория, то существует только одна диаграмма формы J : пустая (похожая на пустую функцию в теории множеств). Конус к пустой диаграмме — это по сути просто объект C. Предел F — это любой объект, который однозначно факторизуется любым другим объектом. Это просто определение терминального объекта .
• Произведения . Если J — дискретная категория , то диаграмма F по сути не что иное, как семейство объектов C , индексированное J. Предел L диаграммы F называется произведением этих объектов. Конус φ состоит из семейства морфизмов φ _X  : L → F ( X ), называемых проекциями произведения. Например, в категории множеств произведения задаются декартовыми произведениями , а проекции — это просто естественные проекции на различные факторы.
  • Степени . Частным случаем произведения является случай, когда диаграмма F является постоянным функтором к объекту X из C. Предел этой диаграммы называется J - ^й степенью X и обозначается X ^J.
• Уравнители . Если J — категория с двумя объектами и двумя параллельными морфизмами из одного объекта в другой, то диаграмма формы J — это пара параллельных морфизмов в C. Предел L такой диаграммы называется уравнителем этих морфизмов.
  • Ядра . Ядро — это частный случай уравнителя, где один из морфизмов — нулевой морфизм .
• Обратные проекции . Пусть F — диаграмма, которая выделяет три объекта X , Y и Z в C , где единственными нетождественными морфизмами являются f  : X → Z и g  : Y → Z. Предел L для F называется обратной проекцией или произведением слоев . Его можно наглядно представить в виде коммутативного квадрата :

• Обратные пределы . Пусть J — направленное множество (рассматриваемое как малая категория путем добавления стрелок i → j тогда и только тогда, когда i ≥ j ), и пусть F  : J ^op → C — диаграмма. Предел F называется обратным пределом или проективным пределом .
• Если J = 1 , категория с одним объектом и морфизмом, то диаграмма формы J по сути является просто объектом X из C. Конус к объекту X является просто морфизмом с областью значений X. Морфизм f  : Y → X является пределом диаграммы X тогда и только тогда, когда f является изоморфизмом . В более общем смысле, если J является любой категорией с начальным объектом i , то любая диаграмма формы J имеет предел, а именно любой объект, изоморфный F ( i ). Такой изоморфизм однозначно определяет универсальный конус к F .
• Топологические пределы . Пределы функций являются частным случаем пределов фильтров , которые связаны с категориальными пределами следующим образом. Для заданного топологического пространства X обозначим через F множество фильтров на X , x ∈ X — точка, V ( x ) ∈ F — фильтр окрестности x , A ∈ F — конкретный фильтр и множество фильтров, более тонких, чем A , и которые сходятся к x . Фильтрам F задается небольшая и тонкая структура категории путем добавления стрелки A → B тогда и только тогда, когда A ⊆ B. Инъекция становится функтором, и выполняется следующая эквивалентность: ${\displaystyle F_{x,A}=\{G\in F\mid V(x)\cup A\subset G\}}$ ${\displaystyle I_{x,A}:F_{x,A}\to F}$

x является топологическим пределом A тогда и только тогда, когда A является категориальным пределом ${\displaystyle I_{x,A}}$

Coпределы

Примерами копределов являются двойственные версии приведенных выше примеров:

• Исходные объекты являются копределами пустых диаграмм.
• Копроизведения — это копределы диаграмм, индексированных по дискретным категориям.
  • Костепени — это копределы постоянных диаграмм из дискретных категорий.
• Коуравнители являются копределами параллельной пары морфизмов.
  • Коядра являются коуравнителями морфизма и параллельного нулевого морфизма.
• Выталкивания являются копределами пары морфизмов с общей областью определения.
• Прямые пределы — это копределы диаграмм, индексированных направленными множествами.

Характеристики

Наличие ограничений

Заданная диаграмма F  : J → C может иметь или не иметь предел (или копредел) в C. Действительно, может даже не быть конуса к F , не говоря уже об универсальном конусе.

Говорят, что категория C имеет пределы формы J , если каждая диаграмма формы J имеет предел в C. В частности, говорят, что категория C имеет

• иметь продукты , если у него есть пределы формы J для каждой небольшой дискретной категории J (у него не обязательно должны быть большие продукты),
• иметь уравнители , если у него есть пределы формы (т.е. каждая параллельная пара морфизмов имеет уравнитель), ${\displaystyle \bullet \rightrightarrows \bullet }$
• иметь обратные пути, если у него есть пределы формы (т.е. каждая пара морфизмов с общей областью значений имеет обратный путь). ${\displaystyle \bullet \rightarrow \bullet \leftarrow \bullet }$

Полная категория — это категория, которая имеет все малые пределы (т.е. все пределы формы J для каждой малой категории J ).

Можно также сделать двойственные определения. Категория имеет копределы формы J , если каждая диаграмма формы J имеет копредел в C. Кополная категория — это категория, которая имеет все малые копределы.

Теорема существования пределов утверждает, что если категория C имеет уравнители и все произведения, индексированные классами Ob( J ) и Hom( J ), то C имеет все пределы формы J . ^{[1] : §V.2 Теория 1} В этом случае предел диаграммы F  : J → C может быть построен как уравнитель двух морфизмов ^{[1] : §V.2 Теория 2}

${\displaystyle s,t:\prod _{i\in \operatorname {Ob} (J)}F(i)\rightrightarrows \prod _{f\in \operatorname {Hom} (J)}F(\operatorname {cod} (f))}$

дано (в компонентной форме)

${\displaystyle {\begin{aligned}s&={\bigl (}F(f)\circ \pi _{\operatorname {dom} (f)}{\bigr )}_{f\in \operatorname {Hom} (J)}\\t&={\bigl (}\pi _{\operatorname {cod} (f)}{\bigr )}_{f\in \operatorname {Hom} (J)}.\end{aligned}}}$

Существует двойственная теорема существования для копределов в терминах коуравнителей и копроизведений. Обе эти теоремы дают достаточные и необходимые условия для существования всех (ко)пределов формы J.

Универсальная собственность

Пределы и копределы являются важными частными случаями универсальных конструкций .

Пусть C — категория, а J — категория малого индекса. Категория функтора C ^J может рассматриваться как категория всех диаграмм формы J в C . Диагональный функтор

${\displaystyle \Delta :{\mathcal {C}}\to {\mathcal {C}}^{\mathcal {J}}}$

— это функтор, который отображает каждый объект N в C в постоянный функтор Δ( N ) : J → C в N. То есть, Δ( N )( X ) = N для каждого объекта X в J и Δ( N )( f ) = id _N для каждого морфизма f в J .

Если задана диаграмма F : J → C (рассматриваемая как объект в C ^J ), естественное преобразование ψ  : Δ( N ) → F (которое является просто морфизмом в категории C ^J ) — это то же самое, что и конус из N в F . Чтобы увидеть это, сначала отметим, что Δ( N )( X ) = N для всех X подразумевает, что компоненты ψ являются морфизмами ψ _X  : N → F ( X ), которые все разделяют область N . Более того, требование, чтобы диаграммы конуса коммутировали, верно просто потому, что это ψ является естественным преобразованием. (Двойственно, естественное преобразование ψ  : F → Δ( N ) — это то же самое, что и коконус из F в N .)

Таким образом, определения пределов и копределов можно переформулировать в виде:

• Предел F — это универсальный морфизм из Δ в F.
• Копредел F — это универсальный морфизм из F в Δ.

Придаточные предложения

Как и все универсальные конструкции, образование пределов и копределов имеет функториальную природу. Другими словами, если каждая диаграмма формы J имеет предел в C (для малых J ), то существует предельный функтор

${\displaystyle \lim :{\mathcal {C}}^{\mathcal {J}}\to {\mathcal {C}}}$

который назначает каждой диаграмме ее предел и каждому естественному преобразованию η : F → G единственный морфизм lim η : lim F → lim G, коммутирующий с соответствующими универсальными конусами. Этот функтор является правым сопряженным диагональному функтору Δ : C → C ^J . Это присоединение дает биекцию между множеством всех морфизмов из N в lim F и множеством всех конусов из N в F

${\displaystyle \operatorname {Hom} (N,\lim F)\cong \operatorname {Cone} (N,F)}$

что естественно в переменных N и F . Коединица этого присоединения — это просто универсальный конус из lim F в F . Если индексная категория J связна ( и непуста ) , то единица присоединения — это изоморфизм, так что lim — левая обратная к Δ. Это неверно, если J не связна. Например, если J — дискретная категория, то компонентами единицы являются диагональные морфизмы δ : N → N ^J .

Двойственно, если каждая диаграмма формы J имеет копредел в C (для малых J ), то существует функтор копредела

${\displaystyle \operatorname {colim} :{\mathcal {C}}^{\mathcal {J}}\to {\mathcal {C}}}$

который назначает каждой диаграмме ее копредел. Этот функтор является левым сопряженным к диагональному функтору Δ : C → C ^J , и один имеет естественный изоморфизм

${\displaystyle \operatorname {Hom} (\operatorname {colim} F,N)\cong \operatorname {Cocone} (F,N).}$

Единицей этого присоединения является универсальный коконус из F в colim F. Если J связен (и непуст), то коединица является изоморфизмом, так что colim является левым обратным к Δ.

Обратите внимание, что как предельный, так и копредельный функторы являются ковариантными функторами.

Как представления функторов

Можно использовать функторы Hom, чтобы связать пределы и копределы в категории C с пределами в Set , категории множеств . Это следует, в частности, из того факта, что ковариантный функтор Hom Hom( N , –) : C → Set сохраняет все пределы в C . По двойственности контравариантный функтор Hom должен переводить копределы в пределы.

Если диаграмма F  : J → C имеет предел в C , обозначаемый lim F , то существует канонический изоморфизм

${\displaystyle \operatorname {Hom} (N,\lim F)\cong \lim \operatorname {Hom} (N,F-)}$

что естественно по переменной N. Здесь функтор Hom( N , F –) является композицией функтора Hom Hom( N , –) с F. Этот изоморфизм является единственным, который сохраняет предельные конусы.

Можно использовать приведенное выше соотношение для определения предела F в C. Первым шагом является наблюдение, что предел функтора Hom( N , F –) можно отождествить с множеством всех конусов от N до F :

${\displaystyle \lim \operatorname {Hom} (N,F-)=\operatorname {Cone} (N,F).}$

Предельный конус задается семейством отображений π _X  : Cone( N , F ) → Hom( N , FX ), где π _X ( ψ ) = ψ _X . Если дан объект L из C вместе с естественным изоморфизмом Φ  : Hom( L , –) → Cone(–, F ), объект L будет пределом F с предельным конусом, заданным Φ _L (id _L ). На причудливом языке это равносильно утверждению, что предел F является представлением функтора Cone(–, F ) : C → Set .

Двойственно, если диаграмма F  : J → C имеет копредел в C , обозначаемый colim F , то существует единственный канонический изоморфизм

${\displaystyle \operatorname {Hom} (\operatorname {colim} F,N)\cong \lim \operatorname {Hom} (F-,N)}$

что естественно по переменной N и уважает копредельные конусы. Отождествляя предел Hom( F –, N ) с множеством Cocone( F , N ), это отношение можно использовать для определения копредела диаграммы F как представления функтора Cocone( F , –).

Взаимообмен пределами и копределами множеств

Пусть I — конечная категория, а J — малая фильтрованная категория . Для любого бифунктора

${\displaystyle F:I\times J\to \mathbf {Set} ,}$

существует естественный изоморфизм

${\displaystyle \operatorname {colim} \limits _{J}\lim _{I}F(i,j)\rightarrow \lim _{I}\operatorname {colim} \limits _{J}F(i,j).}$

На словах, отфильтрованные копределы в Set коммутируют с конечными пределами. Также считается, что малые копределы коммутируют с малыми пределами. ^[2]

Функторы и пределы

Если F  : J → C — диаграмма в C , а G  : C → D — функтор , то с помощью композиции (напомним, что диаграмма — это просто функтор) получается диаграмма GF  : J → D. Тогда возникает естественный вопрос:

«Как пределы GF связаны с пределами F ?»

Сохранение пределов

Функтор G  : C → D индуцирует отображение из Cone( F ) в Cone( GF ): если Ψ — конус из N в F , то GΨ — конус из GN в GF . Говорят, что функтор G сохраняет пределы F , если ( GL , Gφ ) является пределом GF всякий раз, когда ( L , φ ) является пределом F . (Заметим, что если предел F не существует, то G бессмысленно сохраняет пределы F .)

Говорят, что функтор G сохраняет все пределы формы J , если он сохраняет пределы всех диаграмм F  : J → C. Например, можно сказать, что G сохраняет произведения, уравнители, обратные проекции и т. д. Непрерывный функтор — это тот, который сохраняет все малые пределы.

Можно сделать аналогичные определения для копределов. Например, функтор G сохраняет копределы F, если G ( L , φ ) является копределом GF всякий раз, когда ( L , φ ) является копределом F. Конепрерывный функтор — это тот, который сохраняет все малые копределы .

Если C — полная категория , то по приведенной выше теореме о существовании пределов функтор G  : C → D непрерывен тогда и только тогда, когда он сохраняет (малые) произведения и уравнители. Двойственно, G является конепрерывным тогда и только тогда, когда он сохраняет (малые) копроизведения и коуравнители.

Важным свойством сопряженных функторов является то, что каждый правый сопряженный функтор непрерывен, а каждый левый сопряженный функтор конепрерывен. Поскольку сопряженные функторы существуют в изобилии, это дает многочисленные примеры непрерывных и конепрерывных функторов.

Для заданной диаграммы F  : J → C и функтора G  : C → D , если и F, и GF имеют указанные пределы, то существует единственный канонический морфизм

${\displaystyle \tau _{F}:G\lim F\to \lim GF}$

который уважает соответствующие предельные конусы. Функтор G сохраняет пределы F тогда и только тогда, когда это отображение является изоморфизмом. Если категории C и D имеют все пределы формы J , то lim является функтором, а морфизмы τ _F образуют компоненты естественного преобразования

${\displaystyle \tau :G\lim \to \lim G^{J}.}$

Функтор G сохраняет все пределы формы J тогда и только тогда, когда τ является естественным изоморфизмом. В этом смысле можно сказать , что функтор G коммутирует с пределами ( с точностью до канонического естественного изоморфизма).

Сохранение пределов и копределов — это концепция, которая применима только к ковариантным функторам. Для контравариантных функторов соответствующие понятия будут функтором, который переводит копределы в пределы, или функтором, который переводит пределы в копределы.

Снятие ограничений

Говорят, что функтор G  : C → D поднимает пределы для диаграммы F  : J → C , если всякий раз, когда ( L , φ ) является пределом GF, существует предел ( L ′, φ ′) диаграммы F , такой что G ( L ′, φ ′) = ( L , φ ). Функтор G поднимает пределы формы J , если он поднимает пределы для всех диаграмм формы J . Поэтому можно говорить о поднятиях произведений, уравнителях, обратных протягиваниях и т. д. Наконец, говорят, что G поднимает пределы, если он поднимает все пределы. Существуют двойственные определения для поднятия копределов.

Функтор G снимает пределы единственным образом для диаграммы F, если существует единственный прообразный конус ( L ′, φ ′) такой, что ( L ′, φ ′) является пределом F и G ( L ′, φ ′) = ( L , φ ). Можно показать, что G снимает пределы единственным образом тогда и только тогда, когда он снимает пределы и является амнестическим .

Снятие пределов явно связано с сохранением пределов. Если G снимает пределы для диаграммы F и GF имеет предел, то F также имеет предел и G сохраняет пределы F . Из этого следует, что:

• Если G снимает пределы всех форм J и D имеет все пределы форм J , то C также имеет все пределы форм J и G сохраняет эти пределы.
• Если G снимает все малые пределы и D является полным, то C также является полным и G является непрерывным.

Двойственные утверждения для копределов одинаково справедливы.

Создание и отражение ограничений

Пусть F  : J → C — диаграмма. Говорят, что функтор G  : C → D

• создать пределы для F, если всякий раз, когда ( L , φ ) является пределом GF, существует единственный конус ( L ′, φ ′) к F, такой что G ( L ′, φ ′) = ( L , φ ), и, более того , этот конус является пределом F.
• отражают пределы для F, если каждый конус к F , изображение которого под G является пределом GF, уже является пределом F.

Двойственно можно определить создание и отражение копределов.

Легко видеть, что следующие утверждения эквивалентны:

• Функтор G создает пределы.
• Функтор G однозначно снимает ограничения и отражает ограничения.

Существуют примеры функторов, которые однозначно снимают ограничения, но не создают и не отражают их.

Примеры

• Каждый представимый функтор C → Set сохраняет пределы (но не обязательно копределы). В частности, для любого объекта A из C это верно для ковариантного функтора Hom Hom( A ,–) : C → Set .
• Забывающий функтор U :  Grp → Set создает (и сохраняет) все малые пределы и отфильтрованные копределы ; однако U не сохраняет копроизведения. Эта ситуация типична для алгебраических забывающих функторов.
• Свободный функтор F  : Set → Grp (который сопоставляет каждому множеству S свободную группу над S ) является левым сопряженным к забывающему функтору U и, следовательно, является конепрерывным. Это объясняет, почему свободное произведение двух свободных групп G и H является свободной группой, порожденной несвязным объединением генераторов G и H .
• Функтор включения Ab → Grp создает пределы, но не сохраняет копроизведения (копроизведение двух абелевых групп является прямой суммой ).
• Забывчивый функтор Top → Set однозначно снимает пределы и копределы, но не создает ни того, ни другого.
• Пусть Met _c — категория метрических пространств с непрерывными функциями для морфизмов. Забывчивый функтор Met _c → Set поднимает конечные пределы, но не поднимает их однозначно.

Примечание по терминологии

В старой терминологии пределы назывались «обратными пределами» или «проективными пределами», а копределы — «прямыми пределами» или «индуктивными пределами». Это было источником большой путаницы.

Есть несколько способов запомнить современную терминологию. Во-первых,

• корешков,
• побочные продукты,
• соуравнители и
• кодомены

являются типами копределов, тогда как

• ядра,
• продукты
• эквалайзеры и
• домены

являются типами пределов. Во-вторых, префикс "co" подразумевает "первую переменную ". Такие термины, как "когомологии" и "кофибрация", имеют немного более сильную связь с первой переменной, т. е. контравариантной переменной, бифунктора . ${\displaystyle \operatorname {Hom} }$ ${\displaystyle \operatorname {Hom} }$

Смотрите также

• Декартово замкнутая категория  – Тип категории в теории категорий
• Эквалайзер (математика)  – набор аргументов, где две или более функций имеют одинаковое значение.
• Обратный предел  – Конструкция в теории категорий
• Продукт (теория категорий)  – Обобщенный объект в теории категорий

Ссылки

1. Mac Lane, Saunders (1998). Категории для работающего математика . Graduate Texts in Mathematics . Vol. 5 (2nd ed.). Springer-Verlag . ISBN 0-387-98403-8. Збл  0906.18001.
2. коммутативность пределов и копределов в n Lab

Дальнейшее чтение

• Адамек, Иржи; Хорст Херрлих; Джордж Э. Стрекер (1990). Абстрактные и конкретные категории (PDF) . Джон Уайли и сыновья. ISBN 0-471-60922-6.
• Mac Lane, Saunders (1998). Категории для работающих математиков . Graduate Texts in Mathematics . Vol. 5 (2nd ed.). Springer-Verlag . ISBN 0-387-98403-8. Збл  0906.18001.
• Борсо, Фрэнсис (1994). "Пределы". Справочник по категорической алгебре . Энциклопедия математики и ее приложений 50-51, 53 [т.е. 52]. Том 1. Cambridge University Press. ISBN 0-521-44178-1.

Внешние ссылки

• Интерактивная веб-страница, которая генерирует примеры пределов и копределов в категории конечных множеств. Автор Джоселин Пейн.
• Предел в n-й лаборатории