Правильный косой многогранник

Многогранник с неплоскими гранями

В геометрии правильные косые многогранники являются обобщениями набора правильных многогранников , которые включают возможность неплоских граней или вершинных фигур . Коксетер изучал перекошенные вершинные фигуры, которые создавали новые четырехмерные правильные многогранники, а намного позже Бранко Грюнбаум изучал правильные перекошенные грани. ^[1]

Бесконечные правильные косые многогранники, занимающие 3-мерное пространство или больше, называются правильными косыми апейроэдрами .

История

По мнению Коксетера , в 1926 году Джон Флиндерс Петри обобщил понятие правильных косых многоугольников (неплоских многоугольников) на правильные косые многогранники .

Коксетер предложил модифицированный символ Шлефли { l , m | n } для этих фигур, где { l , m } подразумевает фигуру вершины , m l -угольники вокруг вершины и n -угольные отверстия. Их вершинные фигуры представляют собой косые многоугольники , зигзагообразные между двумя плоскостями.

Правильные косые многогранники, представленные { l , m | n } , следуйте этому уравнению:

${\displaystyle 2\cos {\frac {\pi }{l}}\cos {\frac {\pi }{m}}=\cos {\frac {\pi }{n}}}$

Первый набор { l , m | n } повторяет пять выпуклых платоновых тел и одно невыпуклое тело Кеплера – Пуансо :

Конечные правильные косые многогранники

Коксетер также перечислил более широкий набор конечных правильных многогранников в своей статье «Правильные косые многогранники в трех и четырех измерениях и их топологические аналоги».

Точно так же, как бесконечные косые многогранники представляют поверхности многообразия между ячейками выпуклых однородных сот , все конечные формы представляют поверхности многообразия внутри ячеек однородных 4-многогранников .

Многогранники вида {2p, 2q | r} связаны с симметрией группы Кокстера [(p,r,q,r)], которая сводится к линейному [r,p,r], когда q равно 2. Коксетер определяет эту симметрию как [[( p , r , q , r )] ⁺ ], которая, по его словам, изоморфна его абстрактной группе (2 p ,2 q |2, r ). Соответствующие соты имеют расширенную симметрию [[( p , r , q , r )]]. ^[2]

{2p,4|r} представлен гранями {2p} усеченного побитно { r,p,r} однородного 4-многогранника , а {4,2p|r} представлен квадратными гранями усечённого { r,p ,р}.

{4,4|n} создает дуопризму n - n , и, в частности, {4,4|4} помещается внутри тессеракта {4}x{4} .

Кольцо из 60 треугольников образует правильный косой многогранник внутри подмножества граней 600-ячеечного .

{4,5| 4} может быть реализован в пределах 32 вершин и 80 ребер 5-куба , как показано здесь в проекции плоскости Кокстера B5, показывающей вершины и ребра. 80 квадратных граней 5-куба становятся 40 квадратными гранями косого многогранника и 40 квадратными отверстиями.

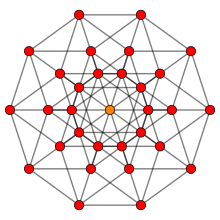
Окончательный набор основан на дальнейшей расширенной форме Кокстера {q1,m|q2,q3...} или с неуказанным q2: {l, m |, q}. Их также можно представить в виде регулярного конечного отображения или { l , m } _{2 q} и группы G ^{l , m , q} . ^[3]

Высшие измерения

Правильные косые многогранники также можно построить в размерностях больше 4 как вложения в правильные многогранники или соты. Например, правильный икосаэдр можно вложить в вершины 6-демикуба ; Коксетер назвал его правильным косым икосаэдром . Додекаэдр аналогичным образом можно встроить в 10-демикуб . ^[4]

Смотрите также

• Наклон многоугольника
• Бесконечный косой многогранник

Примечания

1. Абстрактные правильные многогранники, стр.7, стр.17
2. Коксетер, Правильные и полуправильные многогранники II 2.34)
3. Коксетер и Мозер, Генераторы и отношения для дискретных групп, раздел 8.6. Карты с указанием многоугольников Петри. п. 110
4. Деза, Майкл; Штогрин, Михаил (1998). «Вложение графов правильных мозаик и звездочек-сот в графы гиперкубов и кубических решеток». Продвинутые исследования в области чистой математики . Договоренности – Токио 1998: 77. doi : 10.2969/aspm/02710073 . ISBN 978-4-931469-77-8. Проверено 4 апреля 2020 г.

Рекомендации

• Питер МакМаллен, Четырехмерные правильные многогранники, дискретная и вычислительная геометрия, сентябрь 2007 г., том 38, выпуск 2, стр. 355–387.
• Коксетер , Правильные многогранники , Третье издание, (1973), Дуврское издание, ISBN 0-486-61480-8 
• Калейдоскопы: Избранные сочинения HSM Коксетера , под редакцией Ф. Артура Шерка, Питера Макмаллена, Энтони К. Томпсона, Асии Ивик Вайс, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]  
  • (Документ 2) HSM Coxeter, «Правильные губки, или косые многогранники», Scripta Mathematica 6 (1939) 240–244.
  • (Документ 22) HSM Коксетер, Правильные и полуправильные многогранники I , [Math. Зейт. 46 (1940) 380–407, МР 2,10]
  • (Документ 23) HSM Коксетер, Правильные и полуправильные многогранники II , [Math. Зейт. 188 (1985) 559–591]
• Коксетер , Красота геометрии: двенадцать эссе , Dover Publications, 1999, ISBN 0-486-40919-8 (Глава 5: Правильные косые многогранники в трех и четырех измерениях и их топологические аналоги, Труды Лондонского математического общества, Сер. 2 , Том 43, 1937.)  
  • Коксетер, HSM Правильные косые многогранники в трех и четырех измерениях. Учеб. Лондонская математика. Соц. 43, 33–62, 1937.
• Гарнер, CWL Правильные косые многогранники в гиперболическом трехмерном пространстве. Может. Дж. Математика. 19, 1179–1186, 1967.
• Э. Шульте, Дж. М. Уиллс о правильных косых многогранниках Коксетера, Дискретная математика, том 60, июнь – июль 1986 г., страницы 253–262