
В сферической геометрии сферический круг (часто сокращаемый до круга ) — это геометрическое место точек на сфере, находящихся на постоянном сферическом расстоянии ( сферическом радиусе ) от заданной точки на сфере (полюса или сферического центра ). Это кривая постоянной геодезической кривизны относительно сферы, аналогичная линии или окружности в евклидовой плоскости ; кривые, аналогичные прямым линиям, называются большими кругами , а кривые, аналогичные плоским кругам , называются малыми кругами или меньшими кругами . Если сфера вложена в трехмерное евклидово пространство , ее круги являются пересечениями сферы с плоскостями , а большие круги являются пересечениями с плоскостями, проходящими через центр сферы.
Сферический круг с нулевой геодезической кривизной называется большим кругом и является геодезическим аналогом прямой линии на плоскости. Большой круг разделяет сферу на две равные полусферы , каждая из которых имеет большой круг в качестве своей границы. Если большой круг проходит через точку на сфере, он также проходит через антиподальную точку (единственную самую дальнюю другую точку на сфере). Для любой пары различных неантиподальных точек единственный большой круг проходит через обе. Любые две точки на большом круге разделяют его на две дуги, аналогичные отрезкам на плоскости; более короткая называется малой дугой и является кратчайшим путем между точками, а более длинная называется большой дугой .
Окружность с ненулевой геодезической кривизной называется малой окружностью и аналогична окружности на плоскости. Малая окружность разделяет сферу на два сферических диска или сферических колпачка , каждый из которых имеет окружность в качестве своей границы. Для любой тройки различных неантиподальных точек единственная малая окружность проходит через все три. Любые две точки на малой окружности разделяют ее на две дуги , аналогичные дугам окружностей на плоскости.
Каждый круг имеет два антиподальных полюса (или центра), присущих сфере. Большой круг равноудалён от своих полюсов, в то время как малый круг ближе к одному полюсу, чем к другому. Концентрические круги иногда называют параллельными , потому что они имеют постоянное расстояние друг от друга, и в частности от своего концентрического большого круга, и в этом смысле аналогичны параллельным линиям на плоскости.
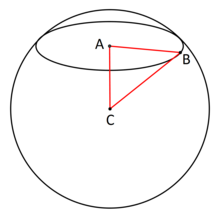
Если сфера изометрически вложена в евклидово пространство , пересечение сферы с плоскостью представляет собой окружность, которую можно интерпретировать внешне по отношению к сфере как евклидову окружность: геометрическое место точек на плоскости на постоянном евклидовом расстоянии ( внешний радиус ) от точки на плоскости ( внешний центр ). Большой круг лежит на плоскости, проходящей через центр сферы, поэтому его внешний радиус равен радиусу самой сферы, а его внешний центр является центром сферы. Малый круг лежит на плоскости, не проходящей через центр сферы, поэтому его внешний радиус меньше радиуса сферы, а его внешний центр является произвольной точкой внутри сферы. Параллельные плоскости разрезают сферу на параллельные (концентрические) малые окружности; пара параллельных плоскостей, касающихся сферы, касается полюсов этих окружностей, а диаметр , проходящий через эти полюса, проходящий через центр сферы и перпендикулярный параллельным плоскостям, называется осью параллельных окружностей.
Пересечение сферы со второй сферой также является окружностью, а пересечение сферы с концентрическим прямым круговым цилиндром или прямым круговым конусом является парой антиподных окружностей.
В географической системе координат на глобусе параллели широты — это малые окружности, а экватор — единственный большой круг. Напротив, все меридианы долготы , в паре с их противоположным меридианом в другом полушарии , образуют большие окружности.