Лемма Шпернера

Теорема о раскраске графа триангуляции

Двумерный случай леммы Шпернера: раскраска Шпернера, в которой закрашены трехцветные треугольники

В математике лемма Шпернера — это комбинаторный результат о раскрасках триангуляции , аналогичный теореме Брауэра о неподвижной точке , которая эквивалентна ей. ^[1] Она утверждает, что каждая раскраска Шпернера (описанная ниже) триангуляции -мерного симплекса содержит ячейку, все вершины которой имеют разные цвета. ${\displaystyle n}$

Первоначальный результат такого рода был доказан Эмануэлем Шпернером в связи с доказательствами инвариантности области . Раскраски Шпернера использовались для эффективного вычисления неподвижных точек и в алгоритмах поиска корней , а также применяются в алгоритмах справедливого дележа (разрезания торта).

Согласно Советской математической энциклопедии (ред. И. М. Виноградов ), родственная теорема 1929 года ( Кнастера , Борсука и Мазуркевича ) также стала известна как лемма Шпернера — этот момент обсуждается в английском переводе (ред. М. Хазевинкель). Сейчас она широко известна как лемма Кнастера–Куратовского–Мазуркевича .

Заявление

Одномерный случай

Пример одномерного случая

В одном измерении лемму Шпернера можно рассматривать как дискретную версию теоремы о промежуточном значении . В этом случае она по сути утверждает, что если дискретная функция принимает только значения 0 и 1, начинается со значения 0 и заканчивается значением 1, то она должна переключать значения нечетное число раз.

Двумерный случай

Двумерный случай упоминается чаще всего. Он формулируется следующим образом:

Подразделим треугольник ABC произвольно на триангуляцию, состоящую из меньших треугольников, встречающихся ребром к ребру. Тогда раскраска Шпернера триангуляции определяется как назначение трех цветов вершинам триангуляции таким образом, что

1. Каждая из трех вершин A , B и C исходного треугольника имеет свой цвет.
2. Вершины, лежащие вдоль любого ребра треугольника ABC, имеют только два цвета, два цвета в конечных точках ребра. Например, каждая вершина на AC должна иметь тот же цвет, что и A или C.

Тогда каждая раскраска Шпернера каждой триангуляции имеет по крайней мере один "радужный треугольник", меньший треугольник в триангуляции, вершины которого окрашены во все три различных цвета. Точнее, должно быть нечетное количество радужных треугольников.

Многомерный случай

В общем случае лемма относится к n -мерному симплексу :

${\displaystyle {\mathcal {A}}=A_{1}A_{2}\ldots A_{n+1}.}$

Рассмотрим любую триангуляцию T , непересекающееся деление на меньшие n -мерные симплексы, снова встречающиеся лицом к лицу. Обозначим функцию раскраски как: ${\displaystyle {\mathcal {A}}}$

${\displaystyle f:S\to \{1,2,3,\dots ,n,n+1\},}$

где S — множество вершин T. Функция раскраски определяет раскраску Шпернера, когда:

1. Вершины большого симплекса окрашены в разные цвета, то есть, без потери общности, f ( A _i ) = i для 1 ≤ i ≤ n + 1 .
2. Вершины T, расположенные на любой k -мерной подграни большого симплекса

   ${\displaystyle A_{i_{1}}A_{i_{2}}\ldots A_{i_{k+1}}}$

   окрашены только цветами

   ${\displaystyle i_{1},i_{2},\ldots ,i_{k+1}.}$

Тогда каждая раскраска Шпернера каждой триангуляции n -мерного симплекса имеет нечетное число экземпляров радужного симплекса , то есть симплекса, вершины которого окрашены во все n + 1 цветов. В частности, должен быть по крайней мере один радужный симплекс.

Доказательства

Доказательство по индукции

Сначала рассмотрим двумерный случай. Рассмотрим граф G, построенный из триангуляции T следующим образом:

Вершины G — это члены T плюс область вне треугольника. Две вершины соединены ребром, если их соответствующие области имеют общую границу с одной конечной точкой, окрашенной в 1, а другой — в 2.

Обратите внимание, что на интервале AB имеется нечетное количество границ, окрашенных в 1-2 цвета (просто потому, что A окрашена в 1 цвет, B окрашена в 2 цвета; и по мере продвижения по AB должно быть нечетное количество смен цвета, чтобы получить разные цвета в начале и в конце). На интервалах BC и CA вообще нет границ, окрашенных в 1-2 цвета. Следовательно, вершина графа G , соответствующая внешней области, имеет нечетную степень. Но известно ( лемма о рукопожатии ), что в конечном графе имеется четное количество вершин с нечетной степенью. Следовательно, оставшийся граф, исключая внешнюю область, имеет нечетное количество вершин с нечетной степенью, соответствующих членам графа T .

Легко видеть, что единственно возможная степень треугольника из T — 0, 1 или 2, и что степень 1 соответствует треугольнику, окрашенному в три цвета: 1, 2 и 3.

Таким образом, мы получили несколько более сильный вывод, который гласит, что в триангуляции T имеется нечетное число (и по крайней мере один) полноцветных треугольников.

Многомерный случай можно доказать индукцией по размерности симплекса. Применяем те же рассуждения, что и в двумерном случае, чтобы заключить, что в n -мерной триангуляции имеется нечетное число полноцветных симплексов.

Комментарий

Простая двумерная триангуляция примера фигуры, раскрашенная и названная в соответствии с предположениями леммы Шпернера.

График, полученный из примера рисунка

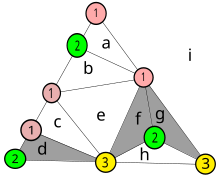
Ниже приводится уточнение приведенного ранее доказательства для читателя, не знакомого с теорией графов .

Эта диаграмма нумерует цвета вершин приведенного ранее примера. Маленькие треугольники, все вершины которых имеют разные номера, заштрихованы на графике. Каждый маленький треугольник становится узлом в новом графике, полученном из триангуляции. Маленькие буквы обозначают области, восемь внутри фигуры, а область i обозначает пространство снаружи нее.

Как было описано ранее, те узлы, которые имеют общее ребро, конечные точки которого пронумерованы 1 и 2, соединяются в производном графе. Например, узел d имеет общее ребро с внешней областью i , и все его вершины имеют разные номера, поэтому он также заштрихован. Узел b не заштрихован, поскольку две вершины имеют одинаковый номер, но он соединен с внешней областью.

Можно добавить новый полностью пронумерованный треугольник, скажем, вставив узел с номером 3 в ребро между 1 и 1 узла a и соединив этот узел с другой вершиной a . Для этого пришлось бы создать пару новых узлов, как в ситуации с узлами f и g .

Доказательство без индукции

Эндрю Макленнан и Раби Турки представили другое доказательство, используя объем симплекса . Оно выполняется в один шаг, без индукции. ^{[2] [3]}

Вычисление симплекса Шпернера

Предположим, что есть d -мерный симплекс с длиной стороны N , и он триангулирован на подсимплексы с длиной стороны 1. Существует функция, которая, учитывая любую вершину триангуляции, возвращает ее цвет. Раскраска гарантированно удовлетворяет граничному условию Шпернера. Сколько раз нам нужно вызвать функцию, чтобы найти радужный симплекс? Очевидно, что мы можем перебрать все вершины триангуляции, число которых равно O( N ^d ), что является полиномом по N при фиксированной размерности. Но можно ли это сделать за время O(poly(log N )), что является полиномом в двоичном представлении N?

Эта проблема была впервые изучена Христосом Пападимитриу . Он ввел класс сложности под названием PPAD , который содержит эту, а также связанные с ней проблемы (такие как поиск неподвижной точки Брауэра ). Он доказал, что нахождение симплекса Шпернера является PPAD-полной задачей даже для d = 3. Примерно 15 лет спустя Чэнь и Дэн доказали PPAD-полноту даже для d = 2. ^[4] Считается, что PPAD-трудные задачи не могут быть решены за время O(poly(log N )).

Обобщения

Подмножества меток

Предположим, что каждая вершина триангуляции может быть помечена несколькими цветами, так что функция раскраски будет иметь вид F  : S → 2 ^{[ n +1]} .

Для каждого подсимплекса набор маркировок на его вершинах является множеством-семейством над множеством цветов [ n + 1] . Это множество-семейство можно рассматривать как гиперграф .

Если для каждой вершины v на грани симплекса цвета в f ( v ) являются подмножеством набора цветов на конечных точках грани, то существует подсимплекс со сбалансированной маркировкой — маркировкой, в которой соответствующий гиперграф допускает идеальное дробное соответствие . Для иллюстрации приведем несколько примеров сбалансированной маркировки для n = 2 :

• ({1}, {2}, {3}) - уравновешено весами (1, 1, 1) .
• ({1,2}, {2,3}, {3,1}) - уравновешено весами (1/2, 1/2, 1/2) .
• ({1,2}, {2,3}, {1}) - уравновешено весами (0, 1, 1) .

Это было доказано Шепли в 1973 году. ^[5] Это комбинаторный аналог леммы KKMS .

Политопальные варианты

Предположим, что у нас есть d -мерный многогранник P с n вершинами. P триангулирован, и каждая вершина триангуляции помечена меткой из {1, …, n }. Каждая главная вершина i помечена i . Подсимплекс называется полностью помеченным, если он d -мерен, и каждая из его d + 1 вершин имеет различную метку. Если каждая вершина в грани F многогранника P помечена одной из меток на конечных точках F , то существует по крайней мере n – d полностью помеченных симплексов. Вот некоторые особые случаи:

• d = n – 1. В этом случае P является симплексом. Политопальная лемма Шпернера гарантирует, что существует по крайней мере 1 полностью помеченный симплекс. То есть, она сводится к лемме Шпернера.
• d = 2. Предположим, что двумерный многоугольник с n вершинами триангулирован и помечен с использованием меток 1, …, n таким образом, что на каждой грани между вершиной i и вершиной i + 1 (mod n ) используются только метки i и i + 1. Тогда существует по крайней мере n – 2 подтреугольника, в которых используются три различные метки.

Общее утверждение было высказано Атанасовым в 1996 году, который доказал его для случая d = 2. [ ^6] Доказательство общего случая было впервые дано де Лоэрой, Петерсоном и Су в 2002 году. ^[7] Они приводят два доказательства: первое неконструктивное и использует понятие множеств камешков ; второе конструктивное и основано на аргументах следования путей в графах .

Менье ^[8] распространил теорему с многогранников на многогранные тела, которые не обязаны быть выпуклыми или односвязными. В частности, если P — многогранник, то множество его граней — многогранное тело. В каждой разметке Шпернера многогранного тела с вершинами v ₁ , …, v _n , имеется по крайней мере:

${\displaystyle n-d-1+\left\lceil {\frac {\min _{i=1}^{n}\deg _{B(P)}(v_{i})}{d}}\right\rceil }$

полностью помеченные симплексы, такие, что любая пара этих симплексов получает две разные маркировки. Степень deg _{B ( P )} ( v _i ) — это количество ребер B ( P ), к которым принадлежит v _i . Поскольку степень не менее d , нижняя граница не менее n – d . Но она может быть больше. Например, для циклического многогранника в 4 измерениях с n вершинами нижняя граница равна:

${\displaystyle n-4-1+\left\lceil {\frac {n-1}{4}}\right\rceil \approx {\frac {5}{4}}n.}$

Мусин ^[9] далее распространил теорему на d -мерные кусочно-линейные многообразия , как с границей, так и без нее.

Асада, Фрик, Пишароди, Полеви, Стоунер, Цанг и Веллнер ^[10] дополнительно расширили теорему на псевдомногообразия с границей и улучшили нижнюю границу числа граней с попарно различными метками.

Кубические варианты

Предположим, что вместо симплекса, триангулированного на подсимплексы, мы имеем n -мерный куб, разделенный на меньшие n -мерные кубы.

Гарольд В. Кун ^[11] доказал следующую лемму. Предположим, что куб [0, M ] ⁿ для некоторого целого числа M разделен на M ⁿ единичных кубов. Предположим, что каждая вершина разбиения помечена меткой из {1, …, n + 1}, так что для каждой вершины v : (1) если v _i = 0 , то метка на v не больше i ; (2) если v _i = M , то метка на v не больше i . Тогда существует единичный куб со всеми метками {1, …, n + 1} (некоторые из них более одного раза). Особый случай n = 2 : предположим, что квадрат разделен на подквадраты, и каждая вершина помечена меткой из {1,2,3}. Левый край помечен 1 (= не больше 1); нижний край помечен 1 или 2 (= не больше 2); верхний край помечен 1 или 3 (= не 2); а правый край помечен 2 или 3 (= не 1). Затем идет квадрат с пометкой 1,2,3.

Другой вариант, связанный с теоремой Пуанкаре–Миранды ^[12] , выглядит следующим образом. Предположим, что куб [0, M ] ⁿ разбит на M ⁿ единичных кубов. Предположим, что каждая вершина помечена двоичным вектором длины n , таким образом, что для каждой вершины v : (1) если v _i = 0 , то координата i метки на v равна 0; (2) если v _i = M , то координата i метки на v равна 1; (3) если две вершины являются соседями, то их метки отличаются не более чем на одну координату. Тогда существует единичный куб, в котором все 2 ⁿ меток различны. В двух измерениях эта теорема может быть сформулирована по-другому: ^[13] в любой маркировке, удовлетворяющей условиям (1) и (2), существует по крайней мере одна ячейка, в которой сумма меток равна 0 [одномерная ячейка с метками (1,1) и (-1,-1) или двумерная ячейка со всеми четырьмя различными метками].

Уолси ^[14] усилил эти два результата, доказав, что число полностью помеченных кубов нечетно.

Мусин ^[13] распространил эти результаты на общие четырехугольники .

Радужные варианты

Предположим, что вместо одной маркировки у нас есть n различных маркировок Шпернера. Мы рассматриваем пары (симплекс, перестановка) такие, что метка каждой вершины симплекса выбирается из другой маркировки (так что для каждого симплекса существует n ! различных пар). Тогда существует по крайней мере n ! полностью маркированных пар. Это было доказано Равиндрой Бапатом ^[15] для любой триангуляции. Более простое доказательство, которое работает только для определенных триангуляций, было представлено позже Су. ^[16]

Другой способ сформулировать эту лемму таков. Предположим, что есть n человек, каждый из которых производит различную маркировку Шпернера одной и той же триангуляции. Тогда существует симплекс и сопоставление людей его вершинам, такое, что каждая вершина помечена ее владельцем по-разному (один человек помечает свою вершину как 1, другой человек помечает свою вершину как 2 и т. д.). Более того, существует по крайней мере n ! таких сопоставлений. Это можно использовать для нахождения разрезания торта без зависти со связанными кусками.

Асада, Фрик, Пишароди, Полеви, Стоунер, Цанг и Веллнер ^[10] распространили эту теорему на псевдомногообразия с краем.

В более общем смысле, предположим, что у нас есть m различных маркировок Шпернера, где m может отличаться от n . Тогда: ^{[17] : Теория 2.1}

1. Для любых положительных целых чисел k ₁ , …, k _{m ,} сумма которых равна m + n – 1 , существует baby-симплекс, на котором для каждого i ∈ {1, …, m } маркировка номера i использует не менее k _i (из n ) различных меток. Более того, каждая метка используется не менее чем одной (из m ) маркировкой.
2. Для любых положительных целых чисел I ₁ , …, I _{m ,} сумма которых равна m + n – 1 , существует младенческий симплекс, на котором для каждого j ∈ {1, …, n } метка j используется по крайней мере l _j (из m ) различных меток.

Обе версии сводятся к лемме Шпернера, когда m = 1 или когда все m маркировок идентичны.

Аналогичные обобщения см . в ^{[18] .}

Ориентированные варианты

Браун и Кейрнс ^[19] усилили лемму Шпернера, рассмотрев ориентацию симплексов. Каждый подсимплекс имеет ориентацию, которая может быть либо +1, либо -1 (если он полностью помечен), либо 0 (если он не полностью помечен). Они доказали, что сумма всех ориентаций симплексов равна +1. В частности, это означает, что существует нечетное число полностью помеченных симплексов.

В качестве примера для n = 3 предположим, что треугольник триангулирован и помечен {1,2,3}. Рассмотрим циклическую последовательность меток на границе треугольника. Определим степень маркировки как количество переключений от 1 до 2 за вычетом количества переключений от 2 до 1. Смотрите примеры в таблице справа. Обратите внимание, что степень будет той же, если мы посчитаем переключения от 2 до 3 за вычетом 3 до 2 или от 3 до 1 за вычетом 1 до 3.

Мусин доказал, что число полностью размеченных треугольников не меньше степени разметки . ^[20] В частности, если степень ненулевая, то существует по крайней мере один полностью размеченный треугольник.

Если разметка удовлетворяет условию Шпернера, то ее степень равна ровно 1: переключения 1-2 и 2-1 есть только в стороне между вершинами 1 и 2, и количество переключений 1-2 должно быть на единицу больше количества переключений 2-1 (при движении от вершины 1 к вершине 2). Поэтому исходная лемма Шпернера следует из теоремы Мусина.

Деревья и циклы

Существует аналогичная лемма о конечных и бесконечных деревьях и циклах . ^[21]

Связанные результаты

Мирзахани и Вондрак ^[22] изучают более слабый вариант разметки Шпернера, в котором единственным требованием является то, чтобы метка i не использовалась на грани, противоположной вершине i . Они называют это допустимой по Шпернеру разметкой . Они показывают, что существуют допустимые по Шпернеру разметки, в которых каждая ячейка содержит не более 4 меток. Они также доказывают оптимальную нижнюю границу числа ячеек, которые должны иметь не менее двух различных меток в каждой допустимой по Шпернеру разметке. Они также доказывают, что для любого допустимого по Шпернеру разбиения правильного симплекса общая площадь границы между частями минимизируется разбиением Вороного .

Приложения

Раскраски Шпернера использовались для эффективного вычисления неподвижных точек . Раскраску Шпернера можно построить таким образом, чтобы полностью помеченные симплексы соответствовали неподвижным точкам заданной функции. Делая триангуляцию все меньше и меньше, можно показать, что предел полностью помеченных симплексов — это в точности неподвижная точка. Следовательно, этот метод дает способ аппроксимировать неподвижные точки. Связанное применение — численное обнаружение периодических орбит и символическая динамика . ^[23] Лемма Шпернера также может использоваться в алгоритмах нахождения корней и алгоритмах справедливого деления ; см. протоколы Симмонса–Су .

Лемма Шпернера является одним из ключевых компонентов доказательства теоремы Монски о том, что квадрат нельзя разрезать на нечетное число равновеликих треугольников . ^[24]

Лемму Шпернера можно использовать для поиска конкурентного равновесия в экономике обмена , хотя существуют более эффективные способы его поиска. ^{[25] : 67}

Спустя пятьдесят лет после первой публикации Шпернер представил обзор развития, влияния и применения своей комбинаторной леммы. ^[26]

Эквивалентные результаты

Существует несколько теорем о неподвижной точке, которые существуют в трех эквивалентных вариантах: алгебраический топологический вариант, комбинаторный вариант и вариант покрытия множеств. Каждый вариант может быть доказан отдельно с использованием совершенно разных аргументов, но каждый вариант также может быть сведен к другим вариантам в его строке. Кроме того, каждый результат в верхней строке может быть выведен из результата под ним в том же столбце. ^[27]

Смотрите также

• Топологическая комбинаторика

Ссылки

1. Флегг, Х. Грэм (1974). От геометрии к топологии . Лондон: English University Press. С. 84–89. ISBN 0-340-05324-0.
2. Анатолий (2010-05-21). "Лемма Шпернера". Блог Math Pages . Получено 2024-07-20 .
3. Макленнан, Эндрю; Турки, Раби (2008). «Использование объема для доказательства леммы Шпернера». Экономическая теория . 35 (3): 593–597. doi :10.1007/s00199-007-0257-0. ISSN  0938-2259. JSTOR  40282878.
4. Чэнь, Си; Дэн, Сяоте (2009-10-17). «О сложности двумерной дискретной задачи с фиксированной точкой». Теоретическая информатика . Автоматы, языки и программирование (ICALP 2006). 410 (44): 4448–4456. doi :10.1016/j.tcs.2009.07.052. ISSN  0304-3975. S2CID  2831759.
5. Шепли, Л. С. (1973-01-01), Ху, Т. К .; Робинсон, Стивен М. (ред.), «О сбалансированных играх без побочных платежей», Математическое программирование , Academic Press, стр. 261–290, ISBN 978-0-12-358350-5, получено 29.06.2020
6. Атанасов, К.Т. (1996), «О лемме Спернера», Studia Scientiarum Mathematicarum Hungarica , 32 (1–2): 71–74, MR  1405126
7. Де Лоэра, Иисус А .; Петерсон, Элиша; Су, Фрэнсис Эдвард (2002), «Политопальное обобщение леммы Шпернера», Журнал комбинаторной теории , Серия A, 100 (1): 1–26, doi : 10.1006/jcta.2002.3274 , MR  1932067
8. Менье, Фредерик (2006-10-01). «Sperner labellings: A combinatorial approach» (Маркировка по Шпернеру: комбинаторный подход). Журнал комбинаторной теории . Серия A. 113 (7): 1462–1475. doi : 10.1016/j.jcta.2006.01.006 . ISSN  0097-3165.
9. Мусин, Олег Р. (2015-05-01). «Расширения леммы Шпернера и Таккера для многообразий». Журнал комбинаторной теории . Серия A. 132 : 172–187. arXiv : 1212.1899 . doi : 10.1016/j.jcta.2014.12.001 . ISSN  0097-3165. S2CID  5699192.
10. Asada, Megumi; Frick, Florian; Pisharody, Vivek; Polevy, Maxwell; Stoner, David; Tsang, Ling Hei; Wellner, Zoe (2018-01-01). «Справедливое разделение и обобщения результатов типа Sperner и KKM». SIAM Journal on Discrete Mathematics . 32 (1): 591–610. arXiv : 1701.04955 . doi : 10.1137/17M1116210. ISSN  0895-4801. S2CID  43932757.
11. Kuhn, HW (1960), «Некоторые комбинаторные леммы в топологии», IBM Journal of Research and Development , 4 (5): 518–524, doi :10.1147/rd.45.0518
12. Михаэль Мюгер (2016), Топология для практикующего математика (PDF) , черновик
13. Мусин, Олег Р. (2015), «Лемма типа Шпернера для четырехангуляций», Московский журнал комбинаторики и теории чисел , 5 (1–2): 26–35, arXiv : 1406.5082 , MR  3476207
14. Wolsey, Laurence A (1 июля 1977 г.). «Кубические леммы Шпернера как приложения обобщенного дополнительного поворота». Журнал комбинаторной теории . Серия A. 23 (1): 78–87. doi : 10.1016/0097-3165(77)90081-4 . ISSN  0097-3165.
15. Бапат, РБ (1989). «Конструктивное доказательство обобщения леммы Шпернера на основе перестановок». Математическое программирование . 44 (1–3): 113–120. doi :10.1007/BF01587081. S2CID  5325605.
16. Su, FE (1999). «Rental Harmony: лемма Спернера в справедливом дележе». The American Mathematical Monthly . 106 (10): 930–942. doi :10.2307/2589747. JSTOR  2589747.
17. Менье, Фредерик; Су, Фрэнсис Эдвард (2019). «Многомаркированные версии лемм Шпернера и Фана и их приложения». Журнал SIAM по прикладной алгебре и геометрии . 3 (3): 391–411. arXiv : 1801.02044 . doi : 10.1137/18M1192548. S2CID  3762597.
18. Асада, Мегуми; Фрик, Флориан; Пишароди, Вивек; Полеви, Максвелл; Стоунер, Дэвид; Цанг, Лин Хей; Веллнер, Зои (2018). «SIAM (Общество промышленной и прикладной математики)». Журнал SIAM по дискретной математике . 32 : 591–610. arXiv : 1701.04955 . doi : 10.1137/17m1116210. S2CID  43932757.
19. Браун, AB; Кэрнс, SS (1961-01-01). «Усиление леммы Шпернера в применении к теории гомологии». Труды Национальной академии наук . 47 (1): 113–114. Bibcode :1961PNAS...47..113B. doi : 10.1073/pnas.47.1.113 . ISSN  0027-8424. PMC 285253 . PMID  16590803. 
20. Олег Р. Мусин (2014). «Вокруг леммы Спернера». arXiv : 1405.7513 [math.CO].
21. Нидермайер, Эндрю; Риццоло, Дуглас; Су, Фрэнсис Эдвард (2014), «Лемма Спернера о дереве», в Барге, Александре; Мусин, Олег Р. (ред.), Дискретная геометрия и алгебраическая комбинаторика , Современная математика, том. 625, Провиденс, Род-Айленд: Американское математическое общество, стр. 77–92, arXiv : 0909.0339 , doi : 10.1090/conm/625/12492, ISBN 9781470409050, MR  3289406, S2CID  115157240
22. Мирзахани, Марьям; Вондрак, Ян (2017), Лебл, Мартин; Нешетржил, Ярослав; Томас, Робин (ред.), «Раскраски Спернера и оптимальное разбиение симплекса», Путешествие по дискретной математике: дань уважения Иржи Матушеку , Чам: Springer International Publishing, стр. 615–631, arXiv : 1611.08339 , doi : 10.1007 /978-3-319-44479-6_25, ISBN 978-3-319-44479-6, S2CID  38668858 , получено 2022-04-25
23. Гидеа, Мариан; Шмало, Ицхак (2018). «Комбинаторный подход к обнаружению неподвижных точек, периодических орбит и символической динамики». Дискретные и непрерывные динамические системы — A. 38 ( 12). Американский институт математических наук (AIMS): 6123–6148. arXiv : 1706.08960 . doi : 10.3934/dcds.2018264 . ISSN  1553-5231. S2CID  119130905.
24. Айгнер, Мартин ; Циглер, Гюнтер М. (2010), «Один квадрат и нечетное число треугольников», Proofs from The Book (4-е изд.), Берлин: Springer-Verlag, стр. 131–138, doi :10.1007/978-3-642-00856-6_20, ISBN 978-3-642-00855-9
25. Скарф, Герберт (1967). «Ядро игры N человек». Econometrica . 35 (1): 50–69. doi :10.2307/1909383. JSTOR  1909383.
26. Sperner, Emanuel (1980), "Пятьдесят лет дальнейшего развития комбинаторной леммы", Численное решение высоконелинейных задач (Sympos. Fixed Point Algorithms and Complementarity Problems, Univ. Southampton, Southampton, 1979) , North-Holland, Amsterdam-New York, стр. 183–197, 199–217, MR  0559121
27. Найман, Кэтрин Л.; Су, Фрэнсис Эдвард (2013), «Эквивалент Борсука–Улама, который напрямую подразумевает лемму Шпернера», The American Mathematical Monthly , 120 (4): 346–354, doi :10.4169/amer.math.monthly.120.04.346, JSTOR  10.4169/amer.math.monthly.120.04.346, MR  3035127

Внешние ссылки

• Доказательство леммы Шпернера в cut-the-knot
• Лемма Шпернера и игра «Треугольник» на сайте с n-богатством.
• Лемма Шпернера в 2D, веб-игра на itch.io.