Парсек

Единица длины, используемая в астрономии.

Парсек (символ: пк ) — единица длины, используемая для измерения больших расстояний до астрономических объектов за пределами Солнечной системы , приблизительно равная 3,26 световым годам или 206 265 астрономическим единицам (а.е.), то есть 30,9  триллиона километров (19,2 триллиона миль ). ^[a] Единица парсек получается с помощью параллакса и тригонометрии и определяется как расстояние, на котором 1 а.е. стягивает угол в одну угловую секунду ^[1] ( ⁠ 1/3600⁠ градуса ). Ближайшая звезда, Проксима Центавра , находится примерно в 1,3 парсека (4,2 световых года) от Солнца : с этого расстояния расстояние между Землей и Солнцем составляет чуть меньше ⁠1/3600⁠ одного градуса зрения. ^[2] Большинство звезд, видимых невооруженным глазом, находятся в пределах нескольких сотен парсеков от Солнца, самые далекие — в нескольких тысячах парсеков, а галактика Андромеды — более чем в 700 000 парсеков. ^[3]

Слово парсек является портманто от «параллакс одной секунды» и было придумано британским астрономом Гербертом Холлом Тернером в 1913 году ^[4] для упрощения астрономических расчетов астрономических расстояний только на основе необработанных данных наблюдений. Отчасти по этой причине эта единица является предпочтительной в астрономии и астрофизике , хотя световой год остается важной единицей в научно-популярных текстах и ​​в общем использовании. Хотя парсеки используются для более коротких расстояний в пределах Млечного Пути , для более крупных масштабов во Вселенной требуются кратные парсекам, включая килопарсеки (кпк) для более удаленных объектов внутри и вокруг Млечного Пути, мегапарсеки (Мпк) для галактик среднего расстояния и гигапарсеки (Гпк) для многих квазаров и самых далеких галактик.

В августе 2015 года Международный астрономический союз (МАС) принял Резолюцию B2, в которой в рамках определения стандартизированной шкалы абсолютной и кажущейся болометрической величины упоминалось существующее явное определение парсека как именно ⁠648 000/π⁠  au, или приблизительно3,085 677 581 491 3673 × 10 ¹⁶  метров (на основе определения астрономической единицы МАС 2012 года). Это соответствует малоугловому определению парсека, встречающемуся во многих астрономических справочниках. ^{[5] [6]}

История и происхождение

Представив себе вытянутый прямоугольный треугольник в космосе, где меньший катет составляет одну а.е. ( астрономическая единица , среднее расстояние от Земли до Солнца ), а противолежащий угол вершины, противоположной этому катету, составляет одну угловую секунду ( 1 ⁄ 3600 градуса), парсек определяется как длина смежного катета. Значение парсека можно вывести с помощью правил тригонометрии . Расстояние от Земли, на котором радиус ее солнечной орбиты составляет одну угловую секунду.

Один из старейших методов, используемых астрономами для вычисления расстояния до звезды , заключается в регистрации разницы в угле между двумя измерениями положения звезды на небе. Первое измерение выполняется с Земли по одну сторону от Солнца, а второе выполняется примерно через полгода, когда Земля находится по другую сторону от Солнца. ^[b] Расстояние между двумя положениями Земли, когда были сделаны два измерения, в два раза больше расстояния между Землей и Солнцем. Разница в угле между двумя измерениями в два раза больше угла параллакса, который образован линиями от Солнца и Земли до звезды в дальней вершине . Тогда расстояние до звезды можно было бы вычислить с помощью тригонометрии. ^[7] Первые успешные опубликованные прямые измерения объекта на межзвездных расстояниях были предприняты немецким астрономом Фридрихом Вильгельмом Бесселем в 1838 году, который использовал этот подход для вычисления расстояния в 3,5 парсека до 61 Лебедя . ^[8]

Параллакс звездного движения из годового параллакса

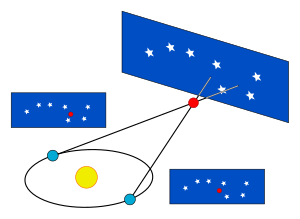
Параллакс звезды определяется как половина углового расстояния , на которое звезда, по-видимому, перемещается относительно небесной сферы, когда Земля вращается вокруг Солнца. Эквивалентно, это противолежащий угол, с точки зрения этой звезды, большой полуоси орбиты Земли. Подставляя параллакс звезды вместо угла в одну угловую секунду в воображаемом прямоугольном треугольнике, длинная сторона треугольника будет измерять расстояние от Солнца до звезды. Парсек можно определить как длину стороны прямоугольного треугольника, смежной с вершиной, занимаемой звездой, угол параллакса которой составляет одну угловую секунду.

Использование парсека в качестве единицы расстояния естественным образом следует из метода Бесселя, поскольку расстояние в парсеках можно вычислить просто как обратную величину угла параллакса в угловых секундах (т. е. если угол параллакса равен 1 угловой секунде, объект находится на расстоянии 1 пк от Солнца; если угол параллакса равен 0,5 угловых секунд, объект находится на расстоянии 2 пк; и т. д.). В этом соотношении не требуются тригонометрические функции , поскольку очень малые углы означают, что можно применить приближенное решение узкого треугольника .

Хотя он мог использоваться и раньше, термин парсек впервые был упомянут в астрономической публикации в 1913 году. Королевский астроном Фрэнк Уотсон Дайсон выразил свою обеспокоенность необходимостью названия для этой единицы расстояния. Он предложил название астрон , но упомянул, что Карл Шарлье предложил сириометр , а Герберт Холл Тернер предложил парсек . ^[4] Именно предложение Тернера закрепилось.

Расчет значения парсека

По определению 2015 года,1 а.е. длины дуги образует угол1″ в центре круга радиуса1 шт . То есть, 1 шт. = 1 а.е./тангенс(1″ ) ≈ 206 264,8 а.е. по определению. ^[9] Преобразование из единиц градус/минута/секунда в радианы ,

${\displaystyle {\frac {1{\text{ pc}}}{1{\text{ au}}}}={\frac {180\times 60\times 60}{\pi }}}$, и

${\displaystyle 1{\text{ au}}=149\,597\,870\,700{\text{ m}}}$(точно по определению AU 2012 года)

Следовательно, (точно по определению 2015 года) $${\displaystyle \pi ~\mathrm {pc} =180\times 60\times 60~\mathrm {au} =180\times 60\times 60\times 149\,597\,870\,700~\mathrm {m} =96\,939\,420\,213\,600\,000~\mathrm {m} }$$

Поэтому,

$${\displaystyle 1~\mathrm {pc} ={\frac {96\,939\,420\,213\,600\,000}{\pi }}~\mathrm {m} =30\,856\,775\,814\,913\,673~\mathrm {m} }$$(с точностью до метра ).

Примерно,

На схеме выше (не в масштабе) S представляет Солнце, а E — Землю в одной точке ее орбиты (например, чтобы образовать прямой угол в точке S ^[b] ). Таким образом, расстояние ES составляет одну астрономическую единицу (а.е.). Угол SDE составляет одну угловую секунду ( ⁠1/3600⁠ градуса ) поэтому по определению D — это точка в пространстве на расстоянии одного парсека от Солнца. С помощью тригонометрии расстояние SD вычисляется следующим образом:

$${\displaystyle {\begin{aligned}\mathrm {SD} &={\frac {\mathrm {ES} }{\tan 1''}}\\&={\frac {\mathrm {ES} }{\tan \left({\frac {1}{60\times 60}}\times {\frac {\pi }{180}}\right)}}\\&\approx {\frac {1\,\mathrm {au} }{{\frac {1}{60\times 60}}\times {\frac {\pi }{180}}}}={\frac {648\,000}{\pi }}\,\mathrm {au} \approx 206\,264.81~\mathrm {au} .\end{aligned}}}$$

Поскольку астрономическая единица определяется как149 597 870 700  м , ^[10] можно рассчитать следующее:

Поэтому, если1  световой год ≈ 9,46 × 10 ¹⁵  м,

Затем1 шт ≈3.261 563 777  св. лет

Следствие гласит, что парсек — это также расстояние, с которого необходимо наблюдать диск диаметром в одну а.е., чтобы его угловой диаметр составлял одну угловую секунду (при размещении наблюдателя в точке D и диска, охватывающего ES ).

Математически для расчета расстояния с учетом полученных угловых измерений с помощью инструментов в угловых секундах формула будет выглядеть так:

$${\displaystyle {\text{Distance}}_{\text{star}}={\frac {{\text{Distance}}_{\text{earth-sun}}}{\tan {\frac {\theta }{3600}}}}}$$

где θ — измеренный угол в угловых секундах, Расстояние _{Земля-Солнце} — константа (1 а.е. или 1,5813 × 10−5 световых ^лет  ). Рассчитанное звездное расстояние будет в той же единице измерения, что и расстояние _{Земля-Солнце} (например, если расстояние _{Земля-Солнце} =¹ а.е. , единица измерения расстояния до _звезды — астрономические единицы; если расстояние _{от Земли до Солнца} = 1,5813 × 10−5  световых лет, единица измерения расстояния до _звезды — световые годы).

Длина парсека, используемая в резолюции B2 МАС 2015 года ^[11] (точно ⁠648 000/π⁠ астрономические единицы) точно соответствует тому, что получено с использованием расчета малых углов. Это отличается от классического определения арктангенса примерно на200 км , т.е. только после 11-й значащей цифры . Поскольку астрономическая единица была определена МАС (2012) как точная длина в метрах, то теперь парсек соответствует точной длине в метрах. С точностью до метра малоугловой парсек соответствует30 856 775 814 913 673  м .

Использование и измерение

Метод параллакса является основным этапом калибровки для определения расстояния в астрофизике ; однако точность измерений угла параллакса с помощью наземного телескопа ограничена примерно0,01″ , и таким образом к звездам не более100 пк . ^[12] Это связано с тем, что атмосфера Земли ограничивает резкость изображения звезды. ^{[ требуется ссылка ]} Космические телескопы не ограничены этим эффектом и могут точно измерять расстояния до объектов, находящихся за пределами наземных наблюдений. В период с 1989 по 1993 год спутник Hipparcos , запущенный Европейским космическим агентством (ESA), измерил параллаксы для примерно100 000 звезд с астрометрической точностью около0,97  мсд и получены точные измерения расстояний до звезд1000 шт. прочь. ^{[13] [14]}

Спутник Gaia Европейского космического агентства , запущенный 19 декабря 2013 года, предназначен для измерения расстояний до одного миллиарда звезд с точностью до20 микросекунд дуги, что приводит к ошибкам в 10% в измерениях до Галактического центра , около8000 пк от нас в созвездии Стрельца . ^[15]

Расстояния в парсеках

Расстояния меньше парсека

Расстояния, выраженные в долях парсека, обычно включают объекты в пределах одной звездной системы. Так, например:

• Одна астрономическая единица (а.е.), расстояние от Солнца до Земли, составляет чуть меньше5 × 10 ⁻⁶  шт .
• Самый дальний космический зонд « Вояджер-1» был0,000 7897  пк от Земли по состоянию на февраль 2024 ^{[обновлять]}г. Вояджер-1 принял46 лет потребовалось, чтобы преодолеть это расстояние.
• Облако Оорта оценивается примерно в0,6 шт в диаметре

Согласно наблюдениям космического телескопа Хаббл , астрофизическая струя , вырывающаяся из активного галактического ядра M87 , образует 20″ и, как полагают, имеет длину 1,5 килопарсека (4892  световых лет ) (струя несколько укорочена с точки зрения Земли).

Парсеки и килопарсеки

Расстояния, выраженные в парсеках (пк), включают расстояния между близлежащими звездами, например, в одном спиральном рукаве или шаровом скоплении . Расстояние в 1000 парсеков (3262 световых лет) обозначается килопарсеком (кпк). Астрономы обычно используют килопарсеки для выражения расстояний между частями галактики или внутри групп галактик . Так, например:

• Проксима Центавра , ближайшая к Земле известная звезда, помимо Солнца, находится на расстоянии около 1,3 парсека (4,24 светового года) по данным прямого измерения параллакса.
• Расстояние до рассеянного скопления Плеяды составляет130 ± 10 шт (420 ± 30 световых лет ) от нас согласно измерению параллакса Hipparcos .
• Центр Млечного Пути находится на расстоянии более 8 килопарсеков (26 000 световых лет) от Земли, а диаметр Млечного Пути составляет примерно 34 килопарсека (110 000 световых лет).
• ESO 383-76 , одна из крупнейших известных галактик , имеет диаметр 540,9 кпк (1,8 миллиона световых лет).
• Галактика Андромеды ( M31 ) находится на расстоянии около 780 килопарсеков (2,5 миллиона световых лет) от Земли.

Мегапарсеки и гигапарсеки

Астрономы обычно выражают расстояния между соседними галактиками и скоплениями галактик в мегапарсеках (МПк). Мегапарсек равен одному миллиону парсеков, или около 3 260 000 световых лет. ^[16] Иногда галактические расстояния указываются в единицах Мпк/ ч (например, «50/ ч  Мпк», также пишется « 50 Мпк ч ⁻¹ »). h — константа (« безразмерная постоянная Хаббла ») в диапазоне 0,5 < h < 0,75, отражающая неопределенность значения постоянной Хаббла H для скорости расширения Вселенной: h = ⁠ЧАС/100 (км/с)/Мпк⁠ . Постоянная Хаббла становится значимой при преобразовании наблюдаемого красного смещения z в расстояние d с использованием формулы d ≈ ⁠с/ЧАС⁠ × z . ^[17]

Один гигапарсек (Гпк) равен одному миллиарду парсеков — одной из самых больших единиц длины, которые обычно используются. Один гигапарсек равен примерно 3,26 миллиарда световых лет, или примерно ⁠1/14⁠ расстояния до горизонта наблюдаемой Вселенной (определяемого космическим микроволновым фоновым излучением ). Астрономы обычно используют гигапарсеки для выражения размеров крупномасштабных структур, таких как размер и расстояние до Великой Китайской стены CfA2 ; расстояния между скоплениями галактик; и расстояния до квазаров .

Например:

• Галактика Андромеды находится на расстоянии около 0,78 Мпк (2,5 миллиона световых лет) от Земли.
• Ближайшее крупное скопление галактик , скопление Девы , находится на расстоянии около 16,5 Мпк (54 миллиона световых лет) от Земли. ^[18]
• Галактика RXJ1242-11 , в которой обнаружено сверхмассивное ядро ​​черной дыры , похожее на ядро ​​Млечного Пути , находится на расстоянии около 200 Мпк (650 миллионов световых лет) от Земли.
• Галактическая нить Геркулеса – Великой Стены Северной Короны , в настоящее время являющаяся крупнейшей известной структурой во Вселенной, имеет диаметр около 3 Гпк (9,8 млрд световых лет).
• Горизонт частиц (граница наблюдаемой Вселенной ) имеет радиус около 14 Гпк (46 миллиардов световых лет). ^[19]

Единицы измерения объема

Для определения количества звезд в Млечном Пути выбираются объемы в кубических килопарсеках ^[c] (кпк ³ ) в различных направлениях. Все звезды в этих объемах подсчитываются, и общее количество звезд определяется статистически. Количество шаровых скоплений, пылевых облаков и межзвездного газа определяется аналогичным образом. Для определения количества галактик в сверхскоплениях выбираются объемы в кубических мегапарсеках ^[c] (Мпк ³ ). Все галактики в этих объемах классифицируются и подсчитываются. Затем общее количество галактик может быть определено статистически. Огромная пустота Волопаса измеряется в кубических мегапарсеках. ^[20]

В физической космологии объемы кубических гигапарсеков ^[c] (Гпк ³ ) выбираются для определения распределения материи в видимой Вселенной и для определения числа галактик и квазаров. Солнце в настоящее время является единственной звездой в своем кубическом парсеке, ^[c] (пк ³ ), но в шаровых скоплениях звездная плотность может быть от100–1000 пк ⁻³ .

Объем наблюдений гравитационно-волновых интерферометров (например, LIGO , Virgo ) выражается в кубических мегапарсеках ^[c] (Мпк ³ ) и по сути представляет собой значение эффективного расстояния в кубе.

Смотрите также

• Аттопарсек
• Измерение расстояния

Примечания

1. Один триллион здесь — это короткая шкала , т. е. 10 ¹² (один миллион миллионов или миллиард в длинной шкале).
2. Наземные наблюдения положения звезды следует проводить, когда Земля находится в самых дальних точках своей орбиты от линии, соединяющей Солнце и звезду, чтобы образовать прямой угол с Солнцем и полную а.е. разделения при наблюдении со стороны звезды.

Ссылки

1. "Космические шкалы расстояний – Млечный Путь" . Получено 24 сентября 2014 г.
2. Бенедикт, Г. Ф.; и др. «Астрометрическая стабильность и точность датчика точного наведения № 3: параллакс и собственное движение Проксимы Центавра» (PDF) . Труды семинара по калибровке телескопа HST . стр. 380–384 . Получено 11 июля 2007 г.
3. "Farthest Stars". StarDate . Техасский университет в Остине . 15 мая 2021 г. . Получено 5 сентября 2021 г. .
4. Dyson, F. W. (март 1913 г.). "Распределение в пространстве звезд в циркумполярном каталоге Кэррингтона". Monthly Notices of the Royal Astronomical Society . 73 (5): 342. Bibcode :1913MNRAS..73..334D. doi : 10.1093/mnras/73.5.334 . [ абзац 14, страница 342 ] Принимая за единицу расстояния R* то, что соответствует параллаксу 1″·0 [… Сноска:] * Для этой единицы расстояния необходимо название. Г-н Шарлье предложил Siriometer , но если можно проигнорировать насилие над греческим языком, можно было бы принять слово Astron . Профессор Тернер предлагает Parsec , что можно принять как сокращенную форму "расстояния, соответствующего параллаксу в одну секунду".
   
5. Кокс, Артур Н., ред. (2000). Астрофизические величины Аллена (4-е изд.). Нью-Йорк: AIP Press / Springer. Bibcode :2000asqu.book.....C. ISBN 978-0387987460.
6. Бинни, Джеймс; Тремейн, Скотт (2008). Galactic Dynamics (2-е изд.). Принстон, Нью-Джерси: Princeton University Press. Bibcode : 2008gady.book.....B. ISBN 978-0-691-13026-2.
7. Научно-исследовательский центр архива астрофизики высоких энергий (HEASARC). "Вывод формулы параллакса". NASA's Imagine the Universe!. Отделение астрофизической науки (ASD) в Центре космических полетов имени Годдарда NASA . Получено 26 ноября 2011 г.
8. Бессель, FW (1838). «Bestimmung der Entfernung des 61sten Sterns des Schwans» [Определение расстояния до 61-й звезды Лебедя]. Астрономические Нахрихтен . 16 (5): 65–96. Бибкод : 1838AN.....16...65B. дои : 10.1002/asna.18390160502.
9. B. Luque; FJ Ballesteros (2019). «Название: К Солнцу и дальше». Nature Physics . 15 (12): 1302. Bibcode : 2019NatPh..15.1302L. doi : 10.1038/s41567-019-0685-3 .
10. Международный астрономический союз, ред. (31 августа 2012 г.), «РЕЗОЛЮЦИЯ B2 о переопределении астрономической единицы длины» (PDF) , РЕЗОЛЮЦИЯ B2 , Пекин: Международный астрономический союз , XXVIII Генеральная ассамблея Международного астрономического союза рекомендует [принято], чтобы астрономическая единица была переопределена в условную единицу длины, равную точно149 597 870 700  м , что соответствует значению, принятому в резолюции B2 МАС 2009 г.
11. Международный астрономический союз, ред. (13 августа 2015 г.), «РЕЗОЛЮЦИЯ B2 о рекомендуемых нулевых точках для шкал абсолютной и видимой болометрической величины» (PDF) , РЕЗОЛЮЦИЯ B2 , Гонолулу: Международный астрономический союз , XXIX Генеральная ассамблея Международного астрономического союза отмечает [4], что парсек определяется как точно (648 000/ ) а.е. согласно определению а.е. в резолюции B2 МАС 2012 г. ${\displaystyle \pi }$
12. Погге, Ричард. «Астрономия 162». Университет штата Огайо.
13. "Миссия космической астрометрии Hipparcos" . Получено 28 августа 2007 г.
14. Турон, Кэтрин. «От Гиппарха к Гиппарку».
15. "GAIA". Европейское космическое агентство .
16. «Почему парсек равен 3,26 световых лет?». Astronomy.com . 1 февраля 2020 г. Получено 20 июля 2021 г.
17. "Структуры галактик: крупномасштабная структура близлежащей вселенной". Архивировано из оригинала 5 марта 2007 года . Получено 22 мая 2007 года .
18. Mei, S.; Blakeslee, J. P.; Côté, P.; et al. (2007). "Обзор скоплений ACS Virgo. XIII. Каталог расстояний SBF и трехмерная структура скопления Virgo". The Astrophysical Journal . 655 (1): 144–162. arXiv : astro-ph/0702510 . Bibcode :2007ApJ...655..144M. doi :10.1086/509598. S2CID  16483538.
19. Lineweaver, Charles H.; Davis, Tamara M. (1 марта 2005 г.). «Заблуждения о Большом взрыве». Scientific American . 292 (3): 36–45. Bibcode :2005SciAm.292c..36L. doi :10.1038/scientificamerican0305-36. Архивировано из оригинала 10 августа 2011 г. Получено 4 февраля 2016 г.
20. Киршнер, Р. П.; Оемлер, А. младший; Шехтер, П. Л.; Шектман, С. А. (1981). "Миллион кубических мегапарсеков пустоты в Волопасе". The Astrophysical Journal . 248 : L57. Bibcode : 1981ApJ...248L..57K. doi : 10.1086/183623. ISSN  0004-637X.

Внешние ссылки

• Guidry, Michael. "Astronomical Distance Scales". Astronomy 162: Stars, Galaxies, and Cosmology . University of Tennessee, Knoxville. Архивировано из оригинала 12 декабря 2012 года . Получено 26 марта 2010 года .
• Меррифилд, Майкл. "pc Parsec". Шестьдесят символов . Брэди Харан для Ноттингемского университета .