Полуэмпирическая формула массы

Формула для приблизительного определения массы ядра на основе количества нуклонов

В ядерной физике полуэмпирическая формула массы ( SEMF ) (иногда также называемая формулой Вайцзеккера , формулой Бете–Вайцзеккера или формулой массы Бете–Вайцзеккера , чтобы отличать ее от процесса Бете–Вайцзеккера ) используется для аппроксимации массы атомного ядра по числу его протонов и нейтронов . Как следует из названия, она основана частично на теории и частично на эмпирических измерениях . Формула представляет собой модель жидкой капли , предложенную Георгием Гамовым ^[1], которая может объяснить большинство членов в формуле и дает грубые оценки значений коэффициентов. Впервые она была сформулирована в 1935 году немецким физиком Карлом Фридрихом фон Вайцзеккером ^[2] , и хотя за прошедшие годы коэффициенты были уточнены, структура формулы остается прежней и сегодня.

Формула дает хорошее приближение для атомных масс и, следовательно, других эффектов. Однако она не может объяснить существование линий большей энергии связи при определенных числах протонов и нейтронов. Эти числа, известные как магические числа , являются основой модели ядерной оболочки .

Модель капли жидкости

Иллюстрация членов полуэмпирической формулы массы в жидкокапельной модели атомного ядра

Модель жидкой капли была впервые предложена Джорджем Гамовым и далее развита Нильсом Бором , Джоном Арчибальдом Уилером и Лизой Мейтнер . ^[3] Она рассматривает ядро ​​как каплю несжимаемой жидкости очень высокой плотности, удерживаемую вместе ядерной силой (остаточный эффект сильной силы ), есть сходство со структурой сферической жидкой капли. Хотя модель жидкой капли является грубой, она учитывает сферическую форму большинства ядер и делает грубый прогноз энергии связи.

Соответствующая формула массы определяется исключительно через число протонов и нейтронов, которые она содержит. Исходная формула Вайцзеккера определяет пять членов:

• Объемная энергия , когда совокупность нуклонов одинакового размера упакована в наименьший объем, каждый внутренний нуклон имеет определенное количество других нуклонов в контакте с ним. Таким образом, эта ядерная энергия пропорциональна объему.
• Поверхностная энергия корректирует предыдущее предположение, что каждый нуклон взаимодействует с тем же числом других нуклонов. Этот член отрицателен и пропорционален площади поверхности, и поэтому примерно эквивалентен поверхностному натяжению жидкости .
• Кулоновская энергия , потенциальная энергия каждой пары протонов. Поскольку это отталкивающая сила, энергия связи уменьшается.
• Энергия асимметрии (также называемая энергией Паули ), которая учитывает принцип исключения Паули . Неравное количество нейтронов и протонов подразумевает заполнение более высоких уровней энергии для одного типа частиц, в то время как более низкие уровни энергии остаются вакантными для другого типа.
• Энергия спаривания , которая объясняет тенденцию возникновения пар протонов и пар нейтронов . Четное число частиц более стабильно, чем нечетное, из-за спиновой связи .

Формула

Энергия связи на нуклон (в МэВ ) показана как функция числа нейтронов N и атомного числа Z , как дано полуэмпирической формулой массы. Пунктирная линия включена для обозначения нуклидов, которые были обнаружены экспериментально.

Разница между предсказанными энергиями и известными энергиями связи, указанными в килоэлектронвольтах. Присутствующие явления можно объяснить дополнительными тонкими терминами, но формула массы не может объяснить наличие линий, четко идентифицируемых по острым пикам в контурах.

Масса атомного ядра для нейтронов , протонов и, следовательно, нуклонов определяется выражением ${\displaystyle N}$ ${\displaystyle Z}$ ${\displaystyle A=N+Z}$

${\displaystyle m=Zm_{\text{p}}+Nm_{\text{n}}-{\frac {E_{\text{B}}(N,Z)}{c^{2}}},}$

где и — масса покоя протона и нейтрона соответственно, а — энергия связи ядра. Полуэмпирическая формула массы утверждает, что энергия связи равна ^[4] ${\displaystyle m_{\text{p}}}$ ${\displaystyle m_{\text{n}}}$ ${\displaystyle E_{\text{B}}}$

${\displaystyle E_{\text{B}}=a_{\text{V}}A-a_{\text{S}}A^{2/3}-a_{\text{C}}{\frac {Z(Z-1)}{A^{1/3}}}-a_{\text{A}}{\frac {(N-Z)^{2}}{A}}\pm \delta (N,Z).}$

Член равен либо нулю, либо , в зависимости от четности и , где для некоторого показателя степени . Обратите внимание, что как , числитель члена можно переписать как . ${\displaystyle \delta (N,Z)}$ ${\displaystyle \pm \delta _{0}}$ ${\displaystyle N}$ ${\displaystyle Z}$ ${\displaystyle \delta _{0}={a_{\text{P}}}{A^{k_{\text{P}}}}}$ ${\displaystyle k_{\text{P}}}$ ${\displaystyle A=N+Z}$ ${\displaystyle a_{\text{A}}}$ ${\displaystyle (A-2Z)^{2}}$

Каждый из членов этой формулы имеет теоретическую основу. Коэффициенты , , , , и определяются эмпирически; хотя они могут быть получены из эксперимента, они обычно выводятся из наименьших квадратов, соответствующих современным данным. Хотя обычно выражаются его основными пятью членами, существуют и другие члены, объясняющие дополнительные явления. Подобно тому, как изменение полиномиальной подгонки изменит ее коэффициенты, взаимодействие между этими коэффициентами при введении новых явлений является сложным; некоторые члены влияют друг на друга, тогда как член в значительной степени независим. ^[5] ${\displaystyle a_{\text{V}}}$ ${\displaystyle a_{\text{S}}}$ ${\displaystyle a_{\text{C}}}$ ${\displaystyle a_{\text{A}}}$ ${\displaystyle a_{\text{P}}}$ ${\displaystyle a_{\text{P}}}$

Объем термина

Этот термин известен как объемный термин . Объем ядра пропорционален A , поэтому этот термин пропорционален объему, отсюда и название. ${\displaystyle a_{\text{V}}A}$

Основой этого термина является сильное ядерное взаимодействие . Сильное взаимодействие влияет как на протоны, так и на нейтроны, и, как и ожидалось, этот термин не зависит от Z. Поскольку число пар, которые можно взять из частиц A , равно , можно было бы ожидать термин, пропорциональный . Однако сильное взаимодействие имеет очень ограниченный диапазон, и данный нуклон может сильно взаимодействовать только со своими ближайшими соседями и следующими ближайшими соседями. Следовательно, число пар частиц, которые фактически взаимодействуют, примерно пропорционально A , что придает термину объема его форму. ${\displaystyle A(A-1)/2}$ ${\displaystyle A^{2}}$

Коэффициент меньше энергии связи, которой обладают нуклоны по отношению к своим соседям ( ), которая имеет порядок 40  МэВ . Это происходит потому, что чем больше число нуклонов в ядре, тем больше их кинетическая энергия из-за принципа исключения Паули . Если рассматривать ядро ​​как ферми-шар из нуклонов , с равным числом протонов и нейтронов, то полная кинетическая энергия равна , с энергией Ферми , которая оценивается как 38  МэВ . Таким образом, ожидаемое значение в этой модели не так уж и далеко от измеренного значения. ${\displaystyle a_{\text{V}}}$ ${\displaystyle E_{\text{b}}}$ ${\displaystyle A}$ ${\displaystyle {\tfrac {3}{5}}A\varepsilon _{\text{F}}}$ ${\displaystyle \varepsilon _{\text{F}}}$ ${\displaystyle a_{\text{V}}}$ ${\displaystyle E_{\text{b}}-{\tfrac {3}{5}}\varepsilon _{\text{F}}\sim 17~\mathrm {MeV} ,}$

Поверхностный термин

Этот термин известен как поверхностный термин . Этот термин, также основанный на сильном взаимодействии, является поправкой к объемному термину. ${\displaystyle a_{\text{S}}A^{2/3}}$

Объемный член предполагает, что каждый нуклон взаимодействует с постоянным числом нуклонов, независимо от A. Хотя это почти верно для нуклонов глубоко внутри ядра, те нуклоны на поверхности ядра имеют меньше ближайших соседей, что оправдывает эту поправку. Это также можно рассматривать как термин поверхностного натяжения, и действительно, похожий механизм создает поверхностное натяжение в жидкостях.

Если объем ядра пропорционален A , то радиус должен быть пропорционален , а площадь поверхности . Это объясняет, почему поверхностный член пропорционален . Также можно вывести, что должно иметь аналогичный порядок величины . ${\displaystyle A^{1/3}}$ ${\displaystyle A^{2/3}}$ ${\displaystyle A^{2/3}}$ ${\displaystyle a_{\text{S}}}$ ${\displaystyle a_{\text{V}}}$

Кулоновский член

Термин или известен как кулоновский или электростатический термин . ${\displaystyle a_{\text{C}}{\frac {Z(Z-1)}{A^{1/3}}}}$ ${\displaystyle a_{\text{C}}{\frac {Z^{2}}{A^{1/3}}}}$

Основой этого термина является электростатическое отталкивание между протонами. В очень грубом приближении ядро ​​можно считать сферой с однородной плотностью заряда . Потенциальная энергия такого распределения заряда может быть показана как

${\displaystyle E={\frac {3}{5}}{\frac {1}{4\pi \varepsilon _{0}}}{\frac {Q^{2}}{R}},}$

где Q — полный заряд, а R — радиус сферы. Значение можно приблизительно рассчитать, используя это уравнение для вычисления потенциальной энергии, используя эмпирический ядерный радиус и Q = Ze . Однако , поскольку электростатическое отталкивание будет существовать только для более чем одного протона, становится : ${\displaystyle a_{\text{C}}}$ ${\displaystyle R\approx r_{0}A^{\frac {1}{3}}}$ ${\displaystyle Z^{2}}$ ${\displaystyle Z(Z-1)}$

${\displaystyle E={\frac {3}{5}}{\frac {1}{4\pi \varepsilon _{0}}}{\frac {Q^{2}}{R}}={\frac {3}{5}}{\frac {1}{4\pi \varepsilon _{0}}}{\frac {(Ze)^{2}}{r_{0}A^{1/3}}}={\frac {3e^{2}Z^{2}}{20\pi \varepsilon _{0}r_{0}A^{1/3}}}\approx {\frac {3e^{2}Z(Z-1)}{20\pi \varepsilon _{0}r_{0}A^{1/3}}}=a_{\text{C}}{\frac {Z(Z-1)}{A^{1/3}}},}$

где теперь электростатическая постоянная Кулона равна ${\displaystyle a_{\text{C}}}$

${\displaystyle a_{\text{C}}={\frac {3e^{2}}{20\pi \varepsilon _{0}r_{0}}}.}$

Используя постоянную тонкой структуры , мы можем переписать значение как ${\displaystyle a_{\text{C}}}$

${\displaystyle a_{\text{C}}={\frac {3}{5}}{\frac {\hbar c\alpha }{r_{0}}}={\frac {3}{5}}{\frac {R_{\text{P}}}{r_{0}}}\alpha m_{\text{p}}c^{2},}$

где - постоянная тонкой структуры, а - радиус ядра , что дает приблизительно 1,25  фемтометра . - приведенная комптоновская длина волны протона , а - масса протона. Это дает приблизительное теоретическое значение 0,691  МэВ , что недалеко от измеренного значения. ${\displaystyle \alpha }$ ${\displaystyle r_{0}A^{1/3}}$ ${\displaystyle r_{0}}$ ${\displaystyle R_{\text{P}}}$ ${\displaystyle m_{\text{p}}}$ ${\displaystyle a_{\text{C}}}$

Термин асимметрии

Иллюстрация основы асимметричного термина

Этот термин известен как термин асимметрии (или термин Паули ). ${\displaystyle a_{\text{A}}{\frac {(N-Z)^{2}}{A}}}$

Теоретическое обоснование этого термина более сложное. Принцип исключения Паули гласит, что никакие два идентичных фермиона не могут занимать в атоме совершенно одинаковое квантовое состояние . На данном уровне энергии для частиц доступно лишь конечное число квантовых состояний. В ядре это означает, что по мере «добавления» большего количества частиц эти частицы должны занимать более высокие энергетические уровни, увеличивая общую энергию ядра (и уменьшая энергию связи). Обратите внимание, что этот эффект не основан ни на одной из фундаментальных сил ( гравитационной , электромагнитной и т. д.), а только на принципе исключения Паули.

Протоны и нейтроны, будучи различными типами частиц, занимают различные квантовые состояния. Можно представить себе два различных «пула» состояний — один для протонов и один для нейтронов. Теперь, например, если в ядре значительно больше нейтронов, чем протонов, некоторые из нейтронов будут иметь более высокую энергию, чем доступные состояния в пуле протонов. Если бы мы могли переместить некоторые частицы из пула нейтронов в пул протонов, другими словами, превратить некоторые нейтроны в протоны, мы бы значительно уменьшили энергию. Дисбаланс между числом протонов и нейтронов приводит к тому, что энергия становится выше, чем она должна быть, для данного числа нуклонов . Это основа для термина асимметрии.

Фактическая форма термина асимметрии может быть снова получена путем моделирования ядра как шара Ферми из протонов и нейтронов. Его полная кинетическая энергия равна

${\displaystyle E_{\text{k}}={\frac {3}{5}}(Z\varepsilon _{\text{F,p}}+N\varepsilon _{\text{F,n}}),}$

где и - энергии Ферми протонов и нейтронов. Поскольку они пропорциональны и соответственно, то получаем ${\displaystyle \varepsilon _{\text{F,p}}}$ ${\displaystyle \varepsilon _{\text{F,n}}}$ ${\displaystyle Z^{2/3}}$ ${\displaystyle N^{2/3}}$

${\displaystyle E_{\text{k}}=C(Z^{5/3}+N^{5/3})}$для некоторой константы C.

Тогда ведущие члены в разложении по разности будут ${\displaystyle N-Z}$

${\displaystyle E_{\text{k}}={\frac {C}{2^{2/3}}}\left(A^{5/3}+{\frac {5}{9}}{\frac {(N-Z)^{2}}{A^{1/3}}}\right)+O{\big (}(N-Z)^{4}{\big )}.}$

В нулевом порядке расширения кинетическая энергия — это просто общая энергия Ферми, умноженная на . Таким образом, мы получаем ${\displaystyle \varepsilon _{\text{F}}\equiv \varepsilon _{\text{F,p}}=\varepsilon _{\text{F,n}}}$ ${\displaystyle {\tfrac {3}{5}}A}$

${\displaystyle E_{\text{k}}={\frac {3}{5}}\varepsilon _{\text{F}}A+{\frac {1}{3}}\varepsilon _{\text{F}}{\frac {(N-Z)^{2}}{A}}+O{\big (}(N-Z)^{4}{\big )}.}$

Первый член вносит вклад в объемный член в полуэмпирической формуле массы, а второй член равен минус члену асимметрии (помните, кинетическая энергия вносит вклад в общую энергию связи со знаком минус ).

${\displaystyle \varepsilon _{\text{F}}}$составляет 38 МэВ , поэтому, вычисляя по уравнению выше, мы получаем только половину измеренного значения. Расхождение объясняется тем, что наша модель не точна: нуклоны фактически взаимодействуют друг с другом и не распределены равномерно по ядру. Например, в оболочечной модели протон и нейтрон с перекрывающимися волновыми функциями будут иметь более сильное взаимодействие между собой и более сильную энергию связи. Это делает энергетически выгодным (т.е. имеющим более низкую энергию) для протонов и нейтронов иметь одинаковые квантовые числа (кроме изоспина ), и, таким образом, увеличивать энергетическую стоимость асимметрии между ними. ${\displaystyle a_{\text{A}}}$

Можно также интуитивно понять термин асимметрии следующим образом. Он должен зависеть от абсолютной разности , а форма проста и дифференцируема , что важно для определенных применений формулы. Кроме того, небольшие различия между Z и N не имеют высоких энергетических затрат. A в знаменателе отражает тот факт, что заданная разность менее значительна для больших значений A. ${\displaystyle |N-Z|}$ ${\displaystyle (N-Z)^{2}}$ ${\displaystyle |N-Z|}$

Термин сопряжения

Величина парного члена в полной энергии связи для четно-четных и нечетно-нечетных ядер как функция массового числа. Показаны два соответствия (синяя и красная линии). Парный член (положительный для четно-четных и отрицательный для нечетно-нечетных ядер) был получен из данных по энергии связи. ^[6]

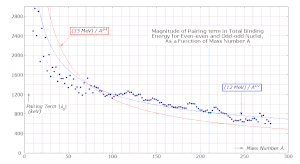
Этот термин известен как термин спаривания (возможно, также известный как парное взаимодействие). Этот термин отражает эффект спиновой связи . Он определяется как ^[7] ${\displaystyle \delta (A,Z)}$

${\displaystyle \delta (A,Z)={\begin{cases}+\delta _{0}&{\text{for even }}Z,N~({\text{even }}A),\\0&{\text{for odd }}A,\\-\delta _{0}&{\text{for odd }}Z,N~({\text{even }}A),\end{cases}}}$

где эмпирически установлено, что имеет значение около 1000 кэВ, медленно уменьшаясь с массовым числом  A. Энергия связи может быть увеличена путем преобразования одного из нечетных протонов или нейтронов в нейтрон или протон, так что нечетный нуклон может образовать пару со своим нечетным соседом, образуя ^{[ необходимо разъяснение ]} и четные Z , N. Пары имеют перекрывающиеся волновые функции и располагаются очень близко друг к другу со связью сильнее, чем любая другая конфигурация. ^[7] Когда член спаривания подставляется в уравнение энергии связи, для четных Z , N член спаривания добавляет энергию связи, а для нечетных Z , N член спаривания удаляет энергию связи. ${\displaystyle \delta _{0}}$

Зависимость от массового числа обычно параметризуется как

${\displaystyle \delta _{0}=a_{\text{P}}A^{k_{\text{P}}}.}$

Значение показателя степени k _P определяется из экспериментальных данных по энергии связи. В прошлом его значение часто принималось равным −3/4, но современные экспериментальные данные показывают, что значение −1/2 ближе к истине:

${\displaystyle \delta _{0}=a_{\text{P}}A^{-1/2}}$или ${\displaystyle \delta _{0}=a_{\text{P}}A^{-3/4}.}$

Из-за принципа исключения Паули ядро ​​имело бы более низкую энергию, если бы число протонов со спином вверх было равно числу протонов со спином вниз. Это также верно для нейтронов. Только если и Z , и N четные, и протоны, и нейтроны могут иметь равное число частиц со спином вверх и спином вниз. Это аналогичный эффект для члена асимметрии.

Фактор нелегко объяснить теоретически. Расчет ферми-шара, который мы использовали выше, основанный на модели жидкой капли, но пренебрегающий взаимодействиями, даст зависимость , как в члене асимметрии. Это означает, что фактический эффект для больших ядер будет больше, чем ожидалось этой моделью. Это должно быть объяснено взаимодействиями между нуклонами. Например, в оболочечной модели два протона с одинаковыми квантовыми числами (кроме спина ) будут иметь полностью перекрывающиеся волновые функции и, таким образом, будут иметь более сильное взаимодействие между собой и более сильную энергию связи. Это делает энергетически выгодным (т. е. имеющим более низкую энергию) для протонов образовывать пары противоположных спинов. То же самое верно и для нейтронов. ${\displaystyle A^{k_{\text{P}}}}$ ${\displaystyle A^{-1}}$

Расчет коэффициентов

Коэффициенты вычисляются путем подгонки под экспериментально измеренные массы ядер. Их значения могут варьироваться в зависимости от того, как они подгоняются под данные и какая единица используется для выражения массы. Несколько примеров показаны ниже.

Формула не учитывает внутреннюю оболочечную структуру ядра.

Таким образом, полуэмпирическая массовая формула хорошо подходит для более тяжелых ядер и плохо подходит для очень легких ядер, особенно 4 He . Для легких ядер обычно лучше использовать модель, которая учитывает эту оболочечную структуру.

Примеры следствий формулы

Максимизируя E _b ( A , Z ) относительно Z , можно найти наилучшее отношение нейтронов и протонов N / Z для заданного атомного веса A . ^[10] Получаем

${\displaystyle N/Z\approx 1+{\frac {a_{\text{C}}}{2a_{\text{A}}}}A^{2/3}.}$

Для легких ядер это отношение составляет примерно 1, но для тяжелых ядер оно растет в хорошем соответствии с экспериментом .

Подставляя вышеуказанное значение Z обратно в E _b , получаем энергию связи как функцию атомного веса, E _b ( A ) . Максимизация E _b ( A )/ A относительно A дает ядро, которое связано наиболее сильно, т.е. наиболее стабильно. Значение, которое мы получаем, равно A = 63 ( медь ), близко к измеренным значениям A = 62 ( никель ) и A = 58 ( железо ) .

Модель жидкой капли также позволяет вычислять барьеры деления для ядер, которые определяют устойчивость ядра к спонтанному делению . Первоначально предполагалось, что элементы с атомным номером выше 104 не могут существовать, поскольку они будут подвергаться делению с очень короткими периодами полураспада, ^[12] хотя эта формула не учитывала стабилизирующие эффекты закрытых ядерных оболочек . Модифицированная формула, учитывающая эффекты оболочек, воспроизводит известные данные и предсказанный остров стабильности (в котором барьеры деления и периоды полураспада, как ожидается, увеличатся, достигнув максимума при замыканиях оболочек), хотя также предполагает возможный предел существования сверхтяжелых ядер за пределами Z  =  120 и N  = 184. ^[12]

Ссылки

1. Гамов, Джордж (1930). «Кривая дефекта массы и ядерное строение». Труды Королевского общества A. 126 ( 803): 632–644. Bibcode : 1930RSPSA.126..632G. doi : 10.1098/rspa.1930.0032 . JSTOR  95297.
2. фон Вайцзеккер, CF (1935). «Zur Theorie der Kernmassen». Zeitschrift für Physik (на немецком языке). 96 (7–8): 431–458. Бибкод : 1935ZPhy...96..431W. дои : 10.1007/BF01337700. S2CID  118231854.
3. Сартори, Э. (2006). Histoire des Femmes Scientifiques de l'Antiquité au XXe siècle (изд. Plon). Париж. стр. 326–328. ISBN 2-259-20288-8.{{cite book}}: CS1 maint: location missing publisher (link)
4. Университет штата Орегон. "Ядерные массы и энергия связи. Урок 3" (PDF) . Архивировано из оригинала (PDF) 30 сентября 2015 г. Получено 30 сентября 2015 г.
5. Кирсон, Майкл В. (2008-01-01). «Взаимное влияние членов в полуэмпирической формуле массы». Nuclear Physics A. 798 ( 1): 29–60. Bibcode : 2008NuPhA.798...29K. doi : 10.1016/j.nuclphysa.2007.10.011. ISSN  0375-9474.
6. G. Audi et al., «Оценка атомной массы AME2012», в Chinese Physics C, 36 (2012/12) стр. 1287–1602.
7. Martin, BR; G. Shaw (2019). Ядерная и элементарная физика: введение (третье изд.). Хобокен, Нью-Джерси. стр. 62. ISBN 978-1-119-34462-9. OCLC  1078954632.{{cite book}}: CS1 maint: location missing publisher (link)
8. Айсберг, Роберт; Резник, Роберт (1985). Квантовая физика атомов, молекул, твердых тел, ядер и частиц (второе издание). John Wiley & Sons. стр. 528. ISBN 0-471-87373-X.
9. Алонсо, Марсело; Финн, Эдвард Дж. (1969). Фундаментальная университетская физика. Том III. Квантовая и статистическая физика . Addison-Wesley Publishing Company . стр. 297.
10. Rohlf, JW (1994). Современная физика от α до Z ⁰ . John Wiley & Sons . ISBN 978-0471572701.
11. Вапстра, АХ (1958). «Атомные массы нуклидов». Во Флюгге, С. (ред.). Внешние свойства атомных ядер / Äussere Eigenschaften der Atomkerne . Энциклопедия физики. Том. 8/38/1. Спрингер . стр. 1–37. Бибкод : 1958HDP....38....1W. дои : 10.1007/978-3-642-45901-6_1. ISBN 978-3-642-45902-3.
12. Möller, P. (2016). «Границы ядерной диаграммы, установленные делением и альфа-распадом» (PDF) . EPJ Web of Conferences . 131 : 03002:1–8. Bibcode :2016EPJWC.13103002M. doi : 10.1051/epjconf/201613103002 .

Источники

• Freedman, R.; Young, H. (2004). Университетская физика Сирса и Земанского с современной физикой (11-е изд.). Pearson Addison Wesley. стр. 1633–1634. ISBN 978-0-8053-8768-1.
• Liverhant, SE (1960). Элементарное введение в физику ядерных реакторов . John Wiley & Sons . стр. 58–62. LCCN  60011725.
• Choppin, G.; Liljenzin, J.-O.; Rydberg, J. (2002). "Ядерная масса и стабильность" (PDF) . Радиохимия и ядерная химия (3-е изд.). Butterworth-Heinemann . стр. 41–57. ISBN 978-0-7506-7463-8.

Внешние ссылки

• Модель капли ядерной жидкости в онлайн-справочнике по гиперфизике в Университете штата Джорджия .
• Модель жидкой капли с параметрами, подобранными из «Первых наблюдений возбужденных состояний в нейтронно-дефицитных ядрах ^160,161 W и ¹⁵⁹ Ta» , Алекс Кинан, докторская диссертация, Ливерпульский университет , 1999 (версия HTML).