stringtranslate.com

теория ВСЭПР

Пример расположения изогнутых электронов (молекула воды). Показывает расположение неспаренных электронов, связанных атомов и углов связи. Угол связи для воды составляет 104,5°.

Теория отталкивания электронных пар валентной оболочки ( VSEPR ) ( / ˈ v ɛ s p ər , v ə ˈ s ɛ p ər / VESP -ər , [ 1] : 410  və- SEP -ər [2] ) — это модель, используемая в химии для предсказания геометрии отдельных молекул по числу электронных пар , окружающих их центральные атомы. [3] Она также называется теорией Джиллеспи-Нихольма в честь двух ее главных разработчиков, Рональда Джиллеспи и Рональда Нихольма .

Предпосылка VSEPR заключается в том, что пары валентных электронов , окружающие атом, имеют тенденцию отталкиваться друг от друга. Чем больше отталкивание, тем выше энергия (менее стабильна) молекулы. Поэтому молекулярная геометрия молекулы, предсказанная VSEPR, — это та, которая имеет как можно меньше этого отталкивания. Джиллеспи подчеркнул, что отталкивание электронов из-за принципа исключения Паули важнее для определения молекулярной геометрии, чем электростатическое отталкивание . [4]

Понимание теории VSEPR вытекает из топологического анализа электронной плотности молекул. Такие методы квантово-химической топологии (QCT) включают функцию локализации электронов (ELF) и квантовую теорию атомов в молекулах (AIM или QTAIM). [4] [5]

История

Идея корреляции между геометрией молекулы и числом пар валентных электронов (как общих, так и неподеленных) была первоначально предложена в 1939 году Рютаро Цучидой в Японии [6] и была независимо представлена ​​в Бейкерианской лекции в 1940 году Невилом Сиджвиком и Гербертом Пауэллом из Оксфордского университета . [7] В 1957 году Рональд Джиллеспи и Рональд Сидней Нихолм из Лондонского университетского колледжа усовершенствовали эту концепцию, превратив ее в более подробную теорию, способную выбирать между различными альтернативными геометриями. [8] [9]

Обзор

Теория VSEPR используется для прогнозирования расположения электронных пар вокруг центральных атомов в молекулах, особенно простых и симметричных молекулах. Центральный атом определяется в этой теории как атом, который связан с двумя или более другими атомами, в то время как конечный атом связан только с одним другим атомом. [1] : 398  Например, в молекуле метилизоцианата (H 3 C-N=C=O) два атома углерода и один азот являются центральными атомами, а три водорода и один кислород являются конечными атомами. [1] : 416  Геометрия центральных атомов и их несвязывающих электронных пар, в свою очередь, определяет геометрию более крупной целой молекулы.

Число электронных пар в валентной оболочке центрального атома определяется после построения структуры Льюиса молекулы и ее расширения для отображения всех связывающих групп и неподеленных пар электронов. [1] : 410–417  В теории VSEPR двойная или тройная связь рассматривается как одинарная связывающая группа. [1] Сумма числа атомов, связанных с центральным атомом, и числа неподеленных пар, образованных его несвязывающими валентными электронами, известна как стерическое число центрального атома.

Предполагается, что электронные пары (или группы, если присутствуют множественные связи) лежат на поверхности сферы с центром на центральном атоме и имеют тенденцию занимать положения, которые минимизируют их взаимное отталкивание за счет максимизации расстояния между ними. [1] : 410–417  [10] Таким образом, количество электронных пар (или групп) определяет общую геометрию, которую они примут. Например, когда есть две электронные пары, окружающие центральный атом, их взаимное отталкивание минимально, когда они лежат на противоположных полюсах сферы. Поэтому центральный атом, как предсказывают, примет линейную геометрию. Если есть 3 электронные пары, окружающие центральный атом, их отталкивание минимизируется путем размещения их в вершинах равностороннего треугольника с центром на атоме. Поэтому предсказываемая геометрия является тригональной . Аналогично, для 4 электронных пар оптимальным расположением является тетраэдрическое . [1] : 410–417 

В качестве инструмента для прогнозирования геометрии, принятой с заданным числом электронных пар, часто используемая физическая демонстрация принципа минимального отталкивания электронных пар использует надутые воздушные шары. При обращении с ними воздушные шары приобретают небольшой поверхностный электростатический заряд, что приводит к принятию примерно тех же геометрий, когда они связаны вместе на своих стеблях, что и соответствующее число электронных пар. Например, пять связанных вместе воздушных шаров принимают тригонально-бипирамидальную геометрию, как и пять связывающих пар молекулы PCl 5 .

Стерическое число

Тетрафторид серы имеет стерическое число 5.

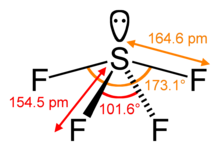
Стерическое число центрального атома в молекуле — это число атомов, связанных с этим центральным атомом, называемое его координационным числом , плюс число неподеленных пар валентных электронов на центральном атоме. [11] Например, в молекуле SF4 центральный атом серы имеет четыре лиганда ; координационное число серы равно четырем. Помимо четырех лигандов , сера также имеет одну неподеленную пару в этой молекуле. Таким образом, стерическое число равно 4 + 1 = 5.

Степень отталкивания

Общая геометрия дополнительно уточняется путем различения связывающих и несвязывающих электронных пар. Связывающая электронная пара, общая в сигма-связи с соседним атомом, находится дальше от центрального атома, чем несвязывающая (неподеленная) пара этого атома, которая удерживается близко к его положительно заряженному ядру. Поэтому теория VSEPR рассматривает отталкивание неподеленной электронной парой как большее, чем отталкивание связывающей парой. Таким образом, когда молекула имеет 2 взаимодействия с разной степенью отталкивания, теория VSEPR предсказывает структуру, в которой неподеленные электронные пары занимают положения, которые позволяют им испытывать меньшее отталкивание. Отталкивания неподеленная пара–неподеленная пара (lp–lp) считаются более сильными, чем отталкивания неподеленная пара–связывающая пара (lp–bp), которые, в свою очередь, считаются более сильными, чем отталкивания связывающая пара–связывающая пара (bp–bp), различия, которые затем определяют решения относительно общей геометрии, когда возможны 2 или более неэквивалентных положения. [1] : 410–417  Например, когда 5 пар валентных электронов окружают центральный атом, они принимают тригонально-бипирамидальную молекулярную геометрию с двумя коллинеарными аксиальными позициями и тремя экваториальными позициями. Электронная пара в аксиальной позиции имеет трех близких экваториальных соседей всего в 90° и четвертого намного дальше в 180°, в то время как экваториальная электронная пара имеет только две соседние пары в 90° и две в 120°. Отталкивание от близких соседей в 90° более важно, так что аксиальные позиции испытывают большее отталкивание, чем экваториальные позиции; следовательно, когда есть неподеленные пары, они имеют тенденцию занимать экваториальные позиции, как показано на диаграммах следующего раздела для стерического числа пять. [10]

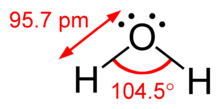
Различие между неподеленными парами и парами связей также может быть использовано для обоснования отклонений от идеализированных геометрий. Например, молекула H 2 O имеет четыре электронные пары в своей валентной оболочке: две неподеленные пары и две пары связей. Четыре электронные пары распределены таким образом, чтобы указывать примерно на вершины тетраэдра. Однако угол связи между двумя связями O–H составляет всего 104,5°, а не 109,5° правильного тетраэдра, поскольку две неподеленные пары (плотность или вероятность которых лежат ближе к ядру кислорода) оказывают большее взаимное отталкивание, чем две пары связей. [1] : 410–417  [10]

Связь более высокого порядка также оказывает большее отталкивание, поскольку электроны пи-связи вносят свой вклад. [10] Например, в изобутилене , (H 3 C) 2 C=CH 2 , угол H 3 C−C=C (124°) больше, чем угол H 3 C−C−CH 3 (111,5°). Однако в карбонат- ионе, CO2−
3, все три связи C−O эквивалентны с углами 120° из-за резонанса .

Метод AX

«Метод AXE» подсчета электронов обычно используется при применении теории VSEPR. Электронные пары вокруг центрального атома представлены формулой AX m E n , где A представляет центральный атом и всегда имеет подразумеваемый нижний индекс один. Каждый X представляет лиганд (атом, связанный с A). Каждый E представляет неподеленную пару электронов на центральном атоме. [1] : 410–417  Общее число X и E известно как стерическое число. Например, в молекуле AX 3 E 2 атом A имеет стерическое число 5.

Когда замещающие атомы (X) не все одинаковы, геометрия все еще приблизительно верна, но углы связи могут немного отличаться от тех, где все внешние атомы одинаковы. Например, углероды двойной связи в алкенах, таких как C 2 H 4, имеют вид AX 3 E 0 , но углы связи не все составляют ровно 120°. Аналогично, SOCl 2 имеет вид AX 3 E 1 , но поскольку заместители X не идентичны, углы X–A–X не все равны.

На основе стерического числа и распределения X и E теория VSEPR делает прогнозы, представленные в следующих таблицах.

Элементы основной группы

Для элементов главной группы существуют стереохимически активные неподеленные пары E , число которых может варьироваться от 0 до 3. Обратите внимание, что геометрии названы только в соответствии с атомными позициями, а не с расположением электронов. Например, описание AX 2 E 1 как изогнутой молекулы означает, что три атома AX 2 не находятся на одной прямой линии, хотя неподеленная пара помогает определить геометрию.

Переходные металлы (модель Кеперта)

Неподеленные пары на атомах переходных металлов обычно стереохимически неактивны, что означает, что их присутствие не изменяет молекулярную геометрию. Например, комплексы гексаакво M(H 2 O) 6 являются все октаэдрическими для M = V 3+ , Mn 3+ , Co 3+ , Ni 2+ и Zn 2+ , несмотря на то, что электронные конфигурации центрального иона металла равны d 2 , d 4 , d 6 , d 8 и d 10 соответственно. [13] : 542  Модель Кеперта игнорирует все неподеленные пары на атомах переходных металлов, так что геометрия вокруг всех таких атомов соответствует геометрии VSEPR для AX n с 0 неподеленными парами E. [15] [13] : 542  Это часто записывается как ML n , где M = металл, а L = лиганд. Модель Киперта предсказывает следующие геометрии для координационных чисел от 2 до 9:

Примеры

Молекула метана (CH 4 ) является тетраэдрической, поскольку имеет четыре пары электронов. Четыре атома водорода расположены в вершинах тетраэдра , а угол связи равен cos −1 (− 1 ⁄ 3 ) ≈ 109° 28′. [16] [17] Это называется типом молекулы AX 4 . Как упоминалось выше, A представляет центральный атом, а X представляет внешний атом. [1] : 410–417 

Молекула аммиака (NH 3 ) имеет три пары электронов, участвующих в связывании, но есть неподеленная пара электронов на атоме азота. [1] : 392–393  Она не связана с другим атомом; однако, она влияет на общую форму посредством отталкивания. Как и в метане выше, есть четыре области электронной плотности. Поэтому общая ориентация областей электронной плотности является тетраэдрической. С другой стороны, есть только три внешних атома. Это называется молекулой типа AX 3 E, потому что неподеленная пара представлена ​​E. [1] : 410–417  По определению, молекулярная форма или геометрия описывает геометрическое расположение только атомных ядер, которое является тригонально-пирамидальным для NH 3 . [1] : 410–417 

Возможны стерические числа 7 или больше, но они встречаются реже. Стерическое число 7 встречается в гептафториде йода (IF 7 ); базовая геометрия для стерического числа 7 — пентагональная бипирамида. [10] Наиболее распространенной геометрией для стерического числа 8 является квадратная антипризматическая геометрия. [18] : 1165  Примерами этого являются октацианомолибдат ( Mo(CN)4−
8) и октафторцирконат ( ZrF4−
8) анионы. [18] : 1165  Ион нонагидридоренат ( ReH2−
9) в нонагидридоренате калия является редким примером соединения со стерическим числом 9, которое имеет трехшапочную тригональную призматическую геометрию. [13] : 254  [18]

Стерические числа выше 9 встречаются очень редко, и неясно, какая геометрия обычно предпочтительна. [19] Возможные геометрии для стерических чисел 10, 11, 12 или 14 — это двушапочная квадратная антипризматическая (или двушапочная додекадельтаэдрическая ), октадекаэдрическая , икосаэдрическая , и двушапочная гексагональная антипризматическая , соответственно. Соединений с такими высокими стерическими числами, включающими монодентатные лиганды, не существует, а те, включающие полидентатные лиганды, часто можно проще анализировать как комплексы с более низкими стерическими числами, когда некоторые полидентатные лиганды рассматриваются как единое целое. [18] : 1165, 1721 

Исключения

Существуют группы соединений, для которых метод VSEPR не может предсказать правильную геометрию.

Некоторые AX2Э0молекулы

Рассчитано, что формы более тяжелых аналогов алкинов элементов 14-й группы (RM≡MR, где M = Si, Ge, Sn или Pb) изогнуты. [20] [21] [22]

Некоторые AX2Э2молекулы

Одним из примеров геометрии AX 2 E 2 является молекулярный оксид лития , Li 2 O, линейная, а не изогнутая структура, которая приписывается его связям, являющимся по существу ионными, и сильному литий-литиевому отталкиванию, которое возникает. [23] Другим примером является O(SiH 3 ) 2 с углом Si–O–Si 144,1°, что сопоставимо с углами в Cl 2 O (110,9°), (CH 3 ) 2 O (111,7°) и N(CH 3 ) 3 (110,9°). [24] Джиллеспи и Робинсон рационализируют угол связи Si–O–Si, основываясь на наблюдаемой способности неподеленной пары лиганда в наибольшей степени отталкивать другие электронные пары, когда электроотрицательность лиганда больше или равна электроотрицательности центрального атома. [24] В O(SiH 3 ) 2 центральный атом более электроотрицателен, а неподеленные пары менее локализованы и более слабо отталкивают. Больший угол связи Si–O–Si является результатом этого и сильного отталкивания лиганд-лиганд относительно большим лигандом -SiH 3 . [24] Берфорд и др. показали с помощью рентгеновской дифракции, что Cl 3 Al–O–PCl 3 имеет линейный угол связи Al–O–P и, следовательно, является не-VSEPR молекулой. [25]

Некоторые AX6Э1и АХ8Э1молекулы

Гексафторид ксенона , имеющий искаженную октаэдрическую геометрию

Некоторые молекулы AX 6 E 1 , например гексафторид ксенона (XeF 6 ) и анионы Te(IV) и Bi(III), TeCl2−
6, ТеБр2−
6, BiCl3−
6, БиБр3−
6и БиИ3−
6, являются октаэдрическими, а не пятиугольными пирамидами, и неподеленная пара не влияет на геометрию в той степени, которая предсказывается VSEPR. [26] Аналогично, ион октафтороксената ( XeF2−
8) в нитрозоний октафтороксенате(VI) [13] : 498  [27] [28] представляет собой квадратную антипризму с минимальным искажением, несмотря на наличие неподеленной пары. Одно из объяснений заключается в том, что стерическое скопление лигандов оставляет мало или совсем не оставляет места для несвязывающей неподеленной пары; [24] другое объяснение заключается в эффекте инертной пары . [13] : 214 

Квадратный плоский ML4комплексы

Модель Кеперта предсказывает, что молекулы переходного металла ML 4 имеют тетраэдрическую форму, и она не может объяснить образование квадратных плоских комплексов. [13] : 542  Большинство таких комплексов демонстрируют конфигурацию ad 8, как и для тетрахлороплатината ( PtCl2−
4) ион. Объяснение формы квадратных плоских комплексов включает электронные эффекты и требует использования теории кристаллического поля . [13] : 562–4 

Комплексы с сильным d-вкладом

Гексаметилвольфрам , комплекс переходного металла, геометрия которого отличается от координации основной группы

Некоторые комплексы переходных металлов с низким числом d-электронов имеют необычную геометрию, которую можно приписать взаимодействию связей подоболочки d. [29] Джиллеспи обнаружил, что это взаимодействие создает связывающие пары, которые также занимают соответствующие антиподальные точки (лиганды, противостоящие друг другу) сферы. [30] [4] Это явление представляет собой электронный эффект, возникающий из-за двудольной формы лежащих в основе гибридных орбиталей sd x . [31] [32] Отталкивание этих связывающих пар приводит к другому набору форм.

Структуры газовой фазы трехатомных галогенидов более тяжелых членов группы 2 (т. е. галогенидов кальция, стронция и бария, MX 2 ), не являются линейными, как предсказывалось, а изогнуты (приблизительные углы X–M–X: CaF 2 , 145°; SrF 2 , 120°; BaF 2 , 108°; SrCl 2 , 130°; BaCl 2 , 115°; BaBr 2 , 115°; BaI 2 , 105°). [36] Джиллеспи предположил , что это также вызвано связывающим взаимодействием лигандов с d-подоболочкой атома металла, что влияет на молекулярную геометрию. [24] [37]

Сверхтяжелые элементы

Релятивистские эффекты на электронных орбиталях сверхтяжелых элементов , как предсказывают, влияют на молекулярную геометрию некоторых соединений. Например, электроны 6d 5/2 в нихонии играют неожиданно сильную роль в связывании, поэтому NhF 3 должен принять Т-образную геометрию вместо тригональной плоской геометрии, как у его более легкого родственника BF 3 . [38] Напротив, дополнительная стабильность электронов 7p 1/2 в теннессине, как предсказывают, делает TsF 3 тригонально-плоским, в отличие от Т-образной геометрии, наблюдаемой для IF 3 и предсказанной для At F 3 ; [39] аналогично, Og F 4 должен иметь тетраэдрическую геометрию, в то время как XeF 4 имеет квадратную плоскую геометрию, а Rn F 4 , как предсказывают, имеет то же самое. [40]

Молекулы с нечетными электронами

Теорию VSEPR можно распространить на молекулы с нечетным числом электронов, рассматривая неспаренный электрон как «полуэлектронную пару» — например, Джиллеспи и Нихольм [8] : 364–365  предположили, что уменьшение угла связи в ряду NO+
2(180°), НЕТ 2 (134°), НЕТ−
2(115°) указывает на то, что данный набор пар связывающих электронов оказывает более слабое отталкивание на один несвязывающий электрон, чем на пару несвязывающих электронов. По сути, они рассматривали диоксид азота как молекулу AX 2 E 0,5 с геометрией, промежуточной между NO+
2и НЕТ−
2. Аналогично, диоксид хлора (ClO 2 ) представляет собой молекулу AX 2 E 1,5 с геометрией, промежуточной между ClO+
2и ClO−
2. [ необходима ссылка ]

Наконец, метильный радикал (CH 3 ) предположительно имеет тригонально-пирамидальную форму, как и метильный анион ( CH−
3), но с большим углом связи (как в тригональном плоском метиловом катионе ( CH+
3)). Однако в этом случае предсказание VSEPR не совсем верно, поскольку CH 3 на самом деле плоский, хотя его искажение до пирамидальной геометрии требует очень мало энергии. [41]

Смотрите также

Ссылки

  1. ^ abcdefghijklmnopqrstu vwxyz aa ab ac ad ae af ag Петруччи, Р. Х.; В. С., Харвуд; Ф. Г., Херринг (2002). Общая химия: принципы и современные приложения (8-е изд.). Prentice-Hall. ISBN 978-0-13-014329-7.
  2. ^ Стокер, Х. Стивен (2009). Общая, органическая и биологическая химия . Cengage Learning. стр. 119. ISBN 978-0-547-15281-3.
  3. ^ abcdefg Джолли, У. Л. (1984). Современная неорганическая химия. McGraw-Hill. С. 77–90. ISBN 978-0-07-032760-3.
  4. ^ abc Gillespie, RJ (2008). «Пятьдесят лет модели VSEPR». Coord. Chem. Rev. 252 ( 12–14): 1315–1327. doi :10.1016/j.ccr.2007.07.007.
  5. ^ Бадер, Ричард Ф.У.; Джиллеспи, Рональд Дж.; Макдугалл, Престон Дж. (1988). «Физическая основа модели VSEPR молекулярной геометрии». J. Am. Chem. Soc . 110 (22): 7329–7336. doi :10.1021/ja00230a009.
  6. ^ Цучида, Рютаро (1939). «Новая простая теория валентности» 新簡易原子價論 [Новая простая теория валентности]. Ниппон Кагаку Кайши (на японском языке). 60 (3): 245–256. дои : 10.1246/nikkashi1921.60.245 .
  7. ^ Сиджвик, Н. В.; Пауэлл, Х. М. (1940). «Бейкеровская лекция. Стереохимические типы и группы валентности». Proc. R. Soc. A. 176 ( 965): 153–180. Bibcode : 1940RSPSA.176..153S. doi : 10.1098/rspa.1940.0084 .
  8. ^ ab Gillespie, RJ ; Nyholm, RS (1957). "Неорганическая стереохимия". Q. Rev. Chem. Soc . 11 (4): 339. doi :10.1039/QR9571100339.
  9. ^ Gillespie, RJ (1970). "Модель отталкивания электронных пар для молекулярной геометрии". J. Chem. Educ . 47 (1): 18. Bibcode :1970JChEd..47...18G. doi :10.1021/ed047p18.
  10. ^ abcdefghijklmn Miessler, GL; Tarr, DA (1999). Неорганическая химия (2-е изд.). Prentice-Hall. стр. 54–62. ISBN 978-0-13-841891-5.
  11. ^ Мисслер, ГЛ; Тарр, Д.А. (1999). Неорганическая химия (2-е изд.). Prentice-Hall. стр. 55. ISBN 978-0-13-841891-5.
  12. ^ Петруччи, Р. Х.; В. С., Харвуд; Ф. Г., Херринг (2002). Общая химия: принципы и современные приложения (8-е изд.). Prentice-Hall. стр. 413–414 (таблица 11.1). ISBN 978-0-13-014329-7.
  13. ^ abcdefghijklmnopqrs Housecroft, CE; Sharpe, AG (2005). Неорганическая химия (2-е изд.). Pearson. ISBN 978-0-130-39913-7.
  14. ^ ab Baran, E. (2000). "Средние амплитуды колебаний пятиугольной пирамиды XeOF−
    5    и ИОФ2−
    5    анионы». J. Fluorine Chem . 101 : 61–63. doi :10.1016/S0022-1139(99)00194-3.
  15. ^ Андерсон, ОП (1983). «Обзоры книг: Неорганическая стереохимия (Дэвид Л. Кеперт)» (PDF) . Acta Crystallographica B . 39 : 527–528. doi : 10.1107/S0108768183002864 . Получено 14 сентября 2020 г. . на основе систематического количественного применения общих идей относительно отталкивания электронных пар
  16. ^ Бриттин, У. Э. (1945). "Валентный угол тетраэдрического атома углерода". J. Chem. Educ . 22 (3): 145. Bibcode : 1945JChEd..22..145B. doi : 10.1021/ed022p145.
  17. ^ «Угол между 2 ножками тетраэдра» Архивировано 2018-10-03 на Wayback Machine – Maze5.net
  18. ^ abcd Wiberg, E.; Holleman, AF (2001). Неорганическая химия . Academic Press. ISBN 978-0-12-352651-9.
  19. ^ Вульфсберг, Гэри (2000). Неорганическая химия . University Science Books. стр. 107. ISBN 9781891389016.
  20. ^ Power, Philip P. (сентябрь 2003 г.). «Кремниевые, германиевые, оловянные и свинцовые аналоги ацетиленов». Chem. Commun. (17): 2091–2101. doi :10.1039/B212224C. PMID  13678155.
  21. ^ Нагасе, Сигеру; Кобаяши, Каору; Такаги, Нозоми (6 октября 2000 г.). «Тройные связи между более тяжелыми элементами 14-й группы. Теоретический подход». J. Organomet. Chem. 11 (1–2): 264–271. doi :10.1016/S0022-328X(00)00489-7.
  22. ^ Секигути, Акира; Киндзё, Рей; Ичинохе, Масааки (сентябрь 2004 г.). «Стабильное соединение, содержащее тройную связь кремний-кремний» (PDF) . Наука . 305 (5691): 1755–1757. Бибкод : 2004Sci...305.1755S. дои : 10.1126/science.1102209. PMID  15375262. S2CID  24416825.[ постоянная мертвая ссылка ]
  23. ^ Беллерт, Д.; Брекенридж, У. Х. (2001). «Спектроскопическое определение длины связи молекулы LiOLi: сильная ионная связь». J. Chem. Phys. 114 (7): 2871. Bibcode : 2001JChPh.114.2871B. doi : 10.1063/1.1349424.
  24. ^ abcde Gillespie, RJ; Robinson, EA (2005). «Модели молекулярной геометрии». Chem. Soc. Rev. 34 (5): 396–407. doi :10.1039/b405359c. PMID  15852152.
  25. ^ Берфорд, Нил; Филлипс, Эндрю; Шурко, Роберт; Василишен, Родерик; Ричардсон, Джон (1997). «Выделение и комплексная характеристика твердого состояния Cl3Al–O–PCl3». Chemical Communications . 1997 (24): 2363–2364 . Получено 3 апреля 2024 г.
  26. ^ Уэллс, А. Ф. (1984). Структурная неорганическая химия (5-е изд.). Oxford Science Publications. ISBN 978-0-19-855370-0.
  27. ^ Peterson, W.; Holloway, H.; Coyle, A.; Williams, M. (сентябрь 1971 г.). «Антипризматическая координация ксенона: структура октафтороксената нитрозония (VI)». Science . 173 (4003): 1238–1239. Bibcode :1971Sci...173.1238P. doi :10.1126/science.173.4003.1238. ISSN  0036-8075. PMID  17775218. S2CID  22384146.
  28. ^ Хансон, Роберт М. (1995). Молекулярное оригами: точные масштабные модели из бумаги . University Science Books. ISBN 978-0-935702-30-9.
  29. ^ ab Kaupp, Martin (2001). ""Non-VSEPR" Structures and Bonding in d0 Systems" (PDF) . Angew. Chem. Int. Ed. Engl. 40 (1): 3534–3565. doi :10.1002/1521-3773(20011001)40:19<3534::AID-ANIE3534>3.0.CO;2-#. PMID  11592184.
  30. ^ Gillespie, Ronald J.; Noury, Stéphane; Pilmé, Julien; Silvi, Bernard (2004). "Исследование функции локализации электронов геометрии молекул d 0 металлов периода 4 от Ca до Mn". Inorg. Chem. 43 (10): 3248–3256. doi :10.1021/ic0354015. PMID  15132634.
  31. ^ Лэндис, CR; Кливленд, T.; Фирман, TK (1995). «Осмысление форм простых гидридов металлов». J. Am. Chem. Soc. 117 (6): 1859–1860. doi :10.1021/ja00111a036.
  32. ^ Landis, CR; Cleveland, T.; Firman, TK (1996). «Структура W(CH3)6». Science . 272 ​​(5259): 179–183. doi : 10.1126/science.272.5259.179f .
  33. ^ Zhai, HJ; Li, S.; Dixon, DA; Wang, LS (2008). «Исследование электронных и структурных свойств кластеров оксида хрома (CrO
    3    )−
    н    и (CrO 3 ) n ( n  = 1–5): Фотоэлектронная спектроскопия и расчеты функционала плотности». Журнал Американского химического общества . 130 (15): 5167–77. doi :10.1021/ja077984d. PMID  18327905.
  34. ^ Кинг, Р. Брюс (2000). «Атомные орбитали, симметрия и координационные полиэдры». Coord. Chem. Rev. 197 : 141–168. doi :10.1016/s0010-8545(99)00226-x.
  35. ^ Хаалан, А.; Хаммель, А.; Райдпал, К.; Волден, Х.В. (1990). «Координационная геометрия газообразного гексаметилвольфрама не является октаэдрической». J. Am. Chem. Soc. 112 (11): 4547–4549. doi :10.1021/ja00167a065.
  36. ^ Гринвуд, Норман Н.; Эрншоу, Алан (1997). Химия элементов (2-е изд.). Баттерворт-Хайнеманн . ISBN 978-0-08-037941-8.
  37. ^ Сейхо, Луис; Барандьяран, Зойла; Хузинага, Сигеру (1991). «Потенциальное исследование с помощью ab initio геометрии равновесной геометрии дигалогенидов щелочноземельных металлов: MX2 (M = Mg, Ca, Sr, Ba; X = F, Cl, Br, I)» (PDF) . Дж. Хим. Физ. 94 (5): 3762. Бибкод : 1991ЖЧФ..94.3762С. дои : 10.1063/1.459748. hdl : 10486/7315 .
  38. ^ Seth, Michael; Schwerdtfeger, Peter; Fægri, Knut (1999). «Химия сверхтяжелых элементов. III. Теоретические исследования соединений элемента 113». Journal of Chemical Physics . 111 (14): 6422–6433. Bibcode : 1999JChPh.111.6422S. doi : 10.1063/1.480168 . hdl : 2292/5178 . S2CID  41854842.
  39. ^ Bae, Ch.; Han, Y.-K.; Lee, Yo. S. (18 января 2003 г.). "Спин-орбитальные и релятивистские эффекты в структурах и стабильности фторидов группы 17 EF 3 (E = I, At и элемент 117): релятивистски-индуцированная стабильность для структуры D 3h (117)F 3 ". Журнал физической химии A . 107 (6): 852–858. Bibcode :2003JPCA..107..852B. doi :10.1021/jp026531m.
  40. ^ Хан, Ён-Кю; Ли, Юн Суп (1999). «Структуры RgFn (Rg = Xe, Rn и элемент 118. n = 2, 4.), рассчитанные двухкомпонентными спин-орбитальными методами. Спин-орбитально-индуцированный изомер (118)F 4 ». Журнал физической химии A . 103 (8): 1104–1108. Bibcode :1999JPCA..103.1104H. doi :10.1021/jp983665k.
  41. ^ Anslyn, EV; Dougherty, DA (2006). Современная физическая органическая химия . University Science Books. стр. 57. ISBN 978-1891389313.

Дальнейшее чтение

Внешние ссылки

В Wikibook A-level Chemistry/OCR (Salters) есть страница на тему: Молекулярная геометрия и неподеленные пары