Монотонная функция

В математике монотонная функция (или монотонная функция ) — это функция между упорядоченными множествами , которая сохраняет или меняет заданный порядок . ^[1]^[2]^[3] Эта концепция впервые возникла в исчислении , а затем была обобщена на более абстрактную теорию теории порядка .

В исчислении и анализе

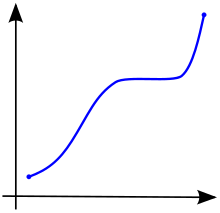
В исчислении функция, определенная на подмножестве действительных чисел с действительными значениями, называется монотонной тогда и только тогда, когда она либо полностью не возрастает, либо совершенно не убывает. ^[2] То есть, согласно рис. 1, функция, которая монотонно возрастает, не обязательно должна только возрастать, она просто не должна убывать. $е$

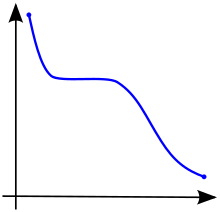
Функция называется монотонно возрастающей (также возрастающей или неубывающей ) ^[3] , если для всех и таких, что имеется , поэтому сохраняется порядок (см. рисунок 1). Аналогично функция называется монотонно убывающей (также убывающей или невозрастающей ) ^[3] , если всякий раз , когда , то , поэтому она меняет порядок на обратный (см. рисунок 2). $х$ $y$ $x\leq y$ ${\ Displaystyle е \! \ влево (х \ вправо) \ leq е \! \ влево (y \ вправо)}$ $е$ $x\leq y$ $f\!\left(x\right)\geq f\!\left(y\right)$

Если порядок в определении монотонности заменить на строгий порядок , то получим более сильное требование. Функция, обладающая этим свойством, называется строго возрастающей (также возрастающей ). ^[3]^[4] Опять же, инвертируя символ порядка, можно найти соответствующее понятие, называемое строго убывающим (также убывающим ). ^[3]^[4] Функция, обладающая любым из этих свойств, называется строго монотонной . Функции, которые являются строго монотонными, являются взаимно однозначными (потому что для не равно , либо или и так, по монотонности, либо или , таким образом .) $\leq$ $<$ $х$ $y$ $x<y$ $x>y$ $f\!\left(x\right)<f\!\left(y\right)$ ${\ Displaystyle е \! \ влево (х \ вправо)> е \! \ влево (у \ вправо)}$ ${\ Displaystyle е \! \ влево (х \ вправо) \ neq е \! \ влево (у \ вправо)}$

Чтобы избежать двусмысленности, термины «слабо монотонно» , «слабо возрастающее » и «слабо убывающее» часто используются для обозначения нестрогой монотонности.

Термины «неубывающий» и «невозрастающий» не следует путать с (гораздо более слабыми) отрицательными определениями «не убывающий» и «не возрастающий». Например, немонотонная функция, показанная на рисунке 3, сначала падает, затем возрастает, затем снова падает. Следовательно, оно не уменьшается и не увеличивается, но оно не является ни неубывающим, ни невозрастающим.

Функция называется абсолютно монотонной на интервале , если производные всех порядков неотрицательны или неположительны во всех точках интервала. $е$ ${\ displaystyle \ left (a, b \ right)}$ $е$

Обратная функция

Все строго монотонные функции обратимы , поскольку они гарантированно имеют взаимно однозначное отображение своего диапазона в свою область определения.

Однако функции, которые являются лишь слабо монотонными, не являются обратимыми, поскольку они постоянны на некотором интервале (и, следовательно, не являются взаимно однозначными).

Функция может быть строго монотонной в ограниченном диапазоне значений и, следовательно, иметь обратную функцию в этом диапазоне, даже если она не является строго монотонной всюду. Например, если строго возрастает в диапазоне , то оно имеет инверсию в диапазоне . ${\ displaystyle y = g (x)}$ $[a,b]$ ${\ displaystyle x = h (y)}$ $[г (а), г (б)]$

Термин «монотонный» иногда используется вместо « строго монотонный» , поэтому источник может утверждать, что все монотонные функции обратимы, хотя на самом деле это означает, что все строго монотонные функции обратимы. ^{[ нужна цитата ]}

Монотонное преобразование

Термин монотонное преобразование (или монотонное преобразование ) также может вызвать путаницу, поскольку он относится к преобразованию с помощью строго возрастающей функции. Так обстоит дело в экономике, когда порядковые свойства функции полезности сохраняются при монотонном преобразовании (см. Также монотонные предпочтения ). ^[5] В этом контексте термин «монотонное преобразование» относится к положительному монотонному преобразованию и предназначен для того, чтобы отличить его от «отрицательного монотонного преобразования», которое меняет порядок чисел. ^[6]

Некоторые основные приложения и результаты

Для монотонной функции справедливы следующие свойства : ${\ displaystyle f \ двоеточие \ mathbb {R} \ to \ mathbb {R} }$

$е$ имеет пределы справа и слева в каждой точке своей области ;
$е$ имеет предел на положительной или отрицательной бесконечности ( ) либо действительного числа, либо . $\pm \infty$ $\infty$ $-\infty$
$е$ может иметь только скачкообразные разрывы ;
$е$ может иметь только счетное число разрывов в своей области. Однако разрывы не обязательно состоят из изолированных точек и могут даже быть плотными на интервале ( a , b ). Например, для любой суммируемой последовательности положительных чисел и любого перечисления рациональных чисел монотонно возрастающая функция $(а_{я})$ ${\ displaystyle (q_ {i})}$ $f(x)=\sum _{q_{i}\leq x}a_{i}$ непрерывен ровно в каждом иррациональном числе (см. рисунок). Это кумулятивная функция распределения дискретной меры рациональных чисел, где – вес . $a_{i}$ $q_{i}$

Эти свойства являются причиной того, почему монотонные функции полезны в технической работе по анализу . Другие важные свойства этих функций включают в себя:

если – монотонная функция, определенная на интервале , то дифференцируема почти всюду на ; т.е. множество чисел в таком, что не дифференцируемо в, имеет нулевую меру Лебега . Кроме того, этот результат невозможно улучшить до счетного: см. функцию Кантора . $е$ $I$ $е$ $I$ $х$ $I$ $е$ $х$
если это множество счетно, то абсолютно непрерывно $е$
если - монотонная функция, определенная на интервале , то она интегрируема по Риману . $е$ $\left[a,b\right]$ $е$

Важным применением монотонных функций является теория вероятностей . Если – случайная величина , ее кумулятивная функция распределения является монотонно возрастающей функцией. $X$ $F_{X}\!\left(x\right)={\text{Prob}}\!\left(X\leq x\right)$

Функция называется унимодальной, если она монотонно возрастает до некоторой точки ( мода ), а затем монотонно убывает.

Когда - строго монотонная функция, то она инъективна в своей области определения, а если - область значений , то существует обратная функция для . Напротив, каждая постоянная функция монотонна, но не инъективна ^[7] и, следовательно, не может иметь обратной. $е$ $е$ $Т$ $е$ $Т$ $е$

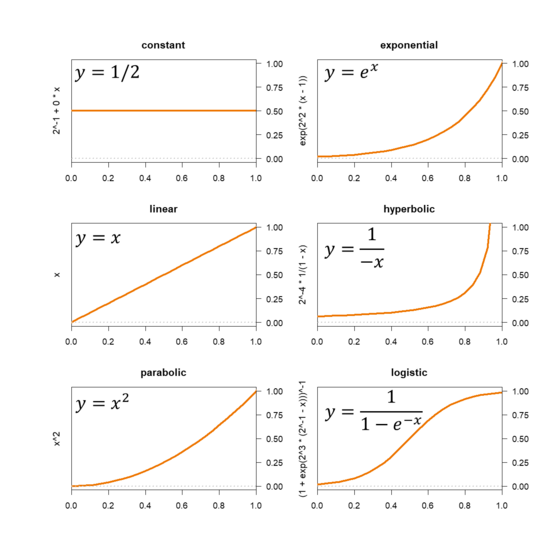
На графике показаны шесть монотонных функций. Их простейшие формы показаны в области графика, а выражения, используемые для их создания, показаны на оси Y.

В топологии

Отображение называется монотонным , если каждый его слой связен ; то есть для каждого элемента множество (возможно, пустое) представляет собой связное подпространство $f:X\to Y$ $y\in Y,$ $f^{-1}(y)$ $X.$

В функциональном анализе

В функциональном анализе топологического векторного пространства оператор (возможно, нелинейный) называется монотонным оператором, если $X$ $T:X\rightarrow X^{*}$

(Tu-Tv,uv)\geq 0\quad \forall u,v\in X.

Теорема Качуровского выпуклые функции банаховых пространствах

Подмножество называется монотонным, если для каждой пары и в , $G$ $X\times X^{*}$ $[u_{1},w_{1}]$ $[u_{2},w_{2}]$ $G$

(w_{1}-w_{2},u_{1}-u_{2})\geq 0.

G

максимальным монотонныммаксимальным монотонныммаксимальное монотонное множество

G(T)

В теории порядка

Теория порядка рассматривает произвольные частично упорядоченные множества и предупорядоченные множества как обобщение действительных чисел. Приведенное выше определение монотонности актуально и в этих случаях. Однако термины «увеличение» и «уменьшение» избегаются, поскольку их обычное графическое представление не применимо к неполным порядкам . Более того, строгие отношения и во многих нетотальных порядках малопригодны, и поэтому для них не вводится дополнительная терминология. $<$ $>$

Обозначаем отношение частичного порядка любого частично упорядоченного множества, монотонную функцию, также называемую изотонной , или $\leq$ сохраняющий порядок , удовлетворяющий свойству

x\leq y\implies f(x)\leq f(y)

для всех $x$ и $y$ в своей области. Композиция двух монотонных отображений также монотонна.

Двойное понятие часто называют антитоном , антимонотонностью или изменением порядка . Следовательно, функция антитона $f$ удовлетворяет свойству

x\leq y\implies f(y)\leq f(x),

для всех $x$ и $y$ в своей области.

Постоянная функция бывает одновременно монотонной и антитонной; и наоборот, если $f$ одновременно монотонна и антитонна и если область определения $f$ представляет собой решетку , то $f$ должно быть постоянным.

Монотонные функции занимают центральное место в теории порядка. Они появляются в большинстве статей на эту тему и в этих местах встречаются примеры из специальных приложений. Некоторые известные специальные монотонные функции являются вложениями порядка (функции, для которых тогда и только тогда и изоморфизмы порядка ( сюръективные вложения порядка). $x\leq y$ $f(x)\leq f(y))$

В контексте поисковых алгоритмов

В контексте поисковых алгоритмов монотонность (также называемая согласованностью) — это условие, применяемое к эвристическим функциям . Эвристика является монотонной, если для каждого узла $n$ и каждого преемника $n'$ из $n$ , сгенерированного любым действием $a$ , предполагаемая стоимость достижения цели из $n$ не превышает стоимость шага достижения $n'$ плюс предполагаемая стоимость достижения цель от $n'$ , $h(n)$

h(n)\leq c\left(n,a,n'\right)+h\left(n'\right).

Это форма неравенства треугольника с $n$ , $n'$ и целью $Gn,$ ближайшей к $n$ . Поскольку любая монотонная эвристика также допустима , монотонность является более строгим требованием, чем допустимость. Некоторые эвристические алгоритмы, такие как A*, могут оказаться оптимальными при условии, что используемая ими эвристика монотонна. ^[8]

В булевых функциях

В булевой алгебре монотонной функцией называется такая функция, что для всех $a i$ и $b i$ из ${0,1}$ , если $a 1 ⩽ b 1$ , $a 2 ⩽ b 2$ , ..., $a n ⩽ b n$ (т. е. Декартово произведение ${0, 1} n$ упорядочено по координатам ), тогда $f(a 1, ..., a n) \leq f(b 1, ..., b n)$ . Другими словами, булева функция является монотонной, если для каждой комбинации входных данных переключение одного из входных данных с ложного на истинное может привести только к переключению вывода с ложного на истинное, а не с истинного на ложное. Графически это означает, что $n$ -арная булева функция является монотонной, когда ее представление в виде $n$ -куба , помеченного значениями истинности, не имеет восходящего края от true до false . (Эта помеченная диаграмма Хассе является двойственной помеченной диаграмме Венна функции , которая является более распространенным представлением для $n \leq 3.$ )

Монотонные логические функции — это именно те, которые можно определить с помощью выражения, объединяющего входные данные (которое может встречаться более одного раза), используя только операторы и и или (в частности, не запрещено). Например, «соблюдаются по крайней мере два из $a$ , $b$ , $c$ » — это монотонная функция от $a$ , $b$ , $c$ , поскольку ее можно записать, например, как (( $a$ и $b$ ) или ( $a$ и $c$ ) или ( $b$ и $c$ )).

Число таких функций от $n$ переменных известно как число Дедекинда $n$ .

Решение SAT , как правило, NP-сложная задача, может быть эффективно достигнуто, когда все задействованные функции и предикаты являются монотонными и логическими. ^[9]

Смотрите также

Примечания

^ Клэпхэм, Кристофер; Николсон, Джеймс (2014). Оксфордский краткий математический словарь (5-е изд.). Издательство Оксфордского университета.
^ аб Стовер, Кристофер. «Монотонная функция». Вольфрам Математический мир . Проверено 29 января 2018 г.
^ abcde «Монотонная функция». Энциклопедия математики . Проверено 29 января 2018 г.
^ аб Спивак, Майкл (1994). Исчисление . Хьюстон, Техас: Publish or Perish, Inc., с. 192. ИСБН 0-914098-89-6.
^ См. раздел «Кардинал против порядковой полезности» в Simon & Blume (1994).
^ Вариан, Хэл Р. (2010). Средний уровень микроэкономики (8-е изд.). WW Нортон и компания. п. 56. ИСБН 9780393934243.
^ если его домен содержит более одного элемента
^ Условия оптимальности: допустимость и непротиворечивость стр. 94–95 (Рассел и Норвиг, 2010).
^ Сэм Бэйлесс, Ной Бэйлесс, Хольгер Х. Хоос и Алан Дж. Ху (2015). SAT Монотонные теории по модулю. Учеб. 29-я конференция AAAI. по искусственному интеллекту. АААИ Пресс. стр. 3702–3709. arXiv : 1406.0043 . дои : 10.1609/aaai.v29i1.9755 .

Библиография

Бартл, Роберт Г. (1976). Элементы реального анализа (второе изд.).
Гретцер, Джордж (1971). Теория решеток: первые понятия и дистрибутивные решетки . ISBN 0-7167-0442-0.
Пембертон, Малькольм; Рау, Николас (2001). Математика для экономистов: Вводный учебник . Издательство Манчестерского университета. ISBN 0-7190-3341-1.
Ренарди, Майкл и Роджерс, Роберт С. (2004). Введение в уравнения в частных производных . Тексты по прикладной математике 13 (Второе изд.). Нью-Йорк: Springer-Verlag. п. 356. ИСБН 0-387-00444-0.
Рисс, Фридьес и Бела Секефальви-Надь (1990). Функциональный анализ . Публикации Courier Dover. ISBN 978-0-486-66289-3.
Рассел, Стюарт Дж.; Норвиг, Питер (2010). Искусственный интеллект: современный подход (3-е изд.). Река Аппер-Сэддл, Нью-Джерси: Прентис-Холл. ISBN 978-0-13-604259-4.
Саймон, Карл П.; Блюм, Лоуренс (апрель 1994 г.). Математика для экономистов (первое изд.). ISBN 978-0-393-95733-4.(Определение 9.31)

Внешние ссылки

«Монотонная функция», Математическая энциклопедия , EMS Press , 2001 [1994]
Сходимость монотонной последовательности Аник Дебнат и Томас Роксло (Школа Харкера), Демонстрационный проект Wolfram .
Вайсштейн, Эрик В. «Монотонная функция». Математический мир .