
В математике знак действительного числа — это его свойство быть либо положительным, либо отрицательным , либо равным 0. В зависимости от местных соглашений ноль может рассматриваться как имеющий свой собственный уникальный знак, не имеющий знака или имеющий как положительный, так и отрицательный знак. В некоторых контекстах имеет смысл различать положительный и отрицательный ноль .
В математике и физике фраза «изменение знака» ассоциируется с заменой объекта на его аддитивную инверсию (умножение на −1 , отрицание), операция, которая не ограничивается действительными числами. Она применяется среди прочих объектов к векторам, матрицам и комплексным числам, которые не предписаны быть только положительными, отрицательными или нулевыми.
Слово «знак» также часто используется для обозначения бинарных аспектов математических или научных объектов, таких как четность и нечетность ( знак перестановки ), направление ориентации или вращения ( по часовой стрелке/против часовой стрелки ), односторонние пределы и другие концепции, описанные в § Другие значения ниже.
Числа из различных числовых систем, такие как целые числа , рациональные числа , комплексные числа , кватернионы , октонионы , ... могут иметь несколько атрибутов, которые фиксируют определенные свойства числа. Числовая система, которая имеет структуру упорядоченного кольца, содержит уникальное число, которое при сложении с любым числом оставляет последнее неизменным. Это уникальное число известно как аддитивный элемент идентичности системы . Например, целые числа имеют структуру упорядоченного кольца. Это число обычно обозначается как 0. Из-за общего порядка в этом кольце существуют числа больше нуля, называемые положительными числами. Другое свойство, необходимое для того, чтобы кольцо было упорядоченным, заключается в том, что для каждого положительного числа существует уникальное соответствующее число меньше 0 , сумма которого с исходным положительным числом равна 0. Эти числа меньше 0 называются отрицательными числами. Числа в каждой такой паре являются их соответствующими аддитивными обратными числами . Этот атрибут числа, который может быть только нулем (0) , положительным (+) или отрицательным (−) , называется его знаком и часто кодируется действительными числами 0 , 1 и −1 соответственно (аналогично тому, как определяется функция знака ). [1] Поскольку рациональные и действительные числа также являются упорядоченными кольцами (фактически упорядоченными полями ), атрибут знака также применяется к этим системам счисления.
Когда знак минус используется между двумя числами, он представляет собой бинарную операцию вычитания. Когда знак минус пишется перед одним числом, он представляет собой унарную операцию получения аддитивной инверсии (иногда называемой отрицанием ) операнда. Абстрактно тогда, разность двух чисел является суммой уменьшаемого с аддитивной инверсией вычитаемого. В то время как 0 является своей собственной аддитивной инверсией ( −0 = 0 ), аддитивная инверсия положительного числа отрицательна, а аддитивная инверсия отрицательного числа положительна. Двойное применение этой операции записывается как −(−3) = 3. Знак плюс в основном используется в алгебре для обозначения бинарной операции сложения и только изредка для подчеркивания положительности выражения.
В общепринятой числовой нотации (используемой в арифметике и других областях) знак числа часто делается явным путем размещения знака плюс или минус перед числом. Например, +3 обозначает «положительные три», а −3 обозначает «отрицательные три» (алгебраически: аддитивное обратное число 3 ). Без определенного контекста (или когда явный знак не указан) число по умолчанию интерпретируется как положительное. Эта нотация устанавливает сильную связь знака минус « − » с отрицательными числами, а знака плюс «+» — с положительными числами.
В рамках соглашения о том, что ноль не является ни положительным, ни отрицательным, определенное знаковое значение 0 может быть присвоено числовому значению 0. Это используется в -функции , как определено для действительных чисел. [1] В арифметике +0 и −0 оба обозначают одно и то же число 0. Обычно нет опасности перепутать значение с его знаком, хотя соглашение о присвоении обоих знаков 0 не позволяет сразу провести такое различие.
В некоторых европейских странах, например, в Бельгии и Франции, 0 считается как положительным, так и отрицательным числом в соответствии с соглашением, изложенным Николя Бурбаки . [2]
В некоторых контекстах, например, при представлении действительных чисел с плавающей точкой в компьютерах, полезно рассматривать знаковые версии нуля, при этом знаковые нули относятся к различным дискретным представлениям чисел ( более подробную информацию см. в разделе Представления чисел со знаком ).
Символы +0 и −0 редко появляются в качестве заменителей 0 + и 0 − , используемых в исчислении и математическом анализе для односторонних пределов (правосторонний предел и левосторонний предел соответственно). Эта нотация относится к поведению функции, когда ее действительная входная переменная приближается к 0 вдоль положительных (соответственно, отрицательных) значений; два предела не обязательно должны существовать или совпадать.
Когда говорят, что 0 не является ни положительным, ни отрицательным, следующие фразы могут относиться к знаку числа:
Когда говорят, что 0 является как положительным, так и отрицательным, для обозначения знака числа используются модифицированные фразы [ требуется ссылка ] :
Например, абсолютное значение действительного числа всегда «неотрицательно», но не обязательно «положительно» в первой интерпретации, тогда как во второй интерпретации оно называется «положительным», хотя и не обязательно «строго положительным».
Та же терминология иногда используется для функций, которые выдают действительные или другие знаковые значения. Например, функция будет называться положительной функцией, если ее значения положительны для всех аргументов ее области определения, или неотрицательной функцией, если все ее значения неотрицательны.
Комплексные числа невозможно упорядочить, поэтому они не могут нести структуру упорядоченного кольца, и, соответственно, не могут быть разделены на положительные и отрицательные комплексные числа. Однако они разделяют атрибут с действительными числами, который называется абсолютным значением или величиной . Величины всегда являются неотрицательными действительными числами, и любому ненулевому числу принадлежит положительное действительное число, его абсолютное значение .
Например, абсолютное значение −3 и абсолютное значение 3 оба равны 3. Это записывается символами как | −3 | = 3 и | 3 | = 3 .
В общем случае любое произвольное действительное значение может быть задано его величиной и знаком. Используя стандартную кодировку, любое действительное значение задается произведением величины и знака в стандартной кодировке. Это отношение можно обобщить для определения знака для комплексных чисел.
Поскольку действительные и комплексные числа образуют поле и содержат положительные действительные числа, они также содержат обратные величины всех ненулевых чисел. Это означает, что любое ненулевое число можно умножить на обратную величину его величины, то есть разделить на его величину. Сразу видно, что частное любого ненулевого действительного числа по его величине дает в точности его знак. По аналогии знак комплексного числа z можно определить как частное z и его величины | z | . Знак комплексного числа является экспонентой произведения его аргумента на мнимую единицу. представляет в некотором смысле его комплексный аргумент. Это следует сравнить со знаком действительных чисел, за исключением Для определения комплексной знаковой функции см. § Комплексная знаковая функция ниже.
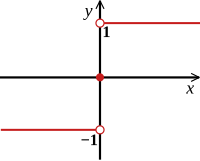
При работе с числами часто бывает удобно иметь их знак в виде числа. Это достигается с помощью функций, которые извлекают знак любого числа и сопоставляют его с предопределенным значением, прежде чем сделать его доступным для дальнейших вычислений. Например, может быть выгодно сформулировать сложный алгоритм только для положительных значений и заботиться о знаке только после этого.
Функция знака или функция знака извлекает знак действительного числа, отображая множество действительных чисел в множество трех действительных чисел. Ее можно определить следующим образом: [1] Таким образом, sgn( x ) равен 1, когда x положителен, и sgn( x ) равен −1, когда x отрицателен. Для ненулевых значений x эта функция также может быть определена формулой, где | x | — абсолютное значение x .
В то время как действительное число имеет одномерное направление, комплексное число имеет двумерное направление. Комплексная функция знака требует величины своего аргумента z = x + iy , который может быть вычислен как
Аналогично предыдущему, функция комплексного знака извлекает комплексный знак комплексного числа, отображая множество ненулевых комплексных чисел в множество унимодулярных комплексных чисел, а 0 в 0 : Ее можно определить следующим образом:
Пусть z также выражается через свою величину и один из своих аргументов φ как z = | z |⋅ e iφ , тогда [3]
Это определение также может быть распознано как нормализованный вектор, то есть вектор, направление которого не меняется, а длина фиксирована на единице . Если исходное значение было R,θ в полярной форме, то sign(R, θ) равно 1 θ. Расширение sign() или signum() на любое количество измерений очевидно, но это уже было определено как нормализация вектора.
В ситуациях, когда для атрибута есть ровно две возможности на равных основаниях, они часто помечаются условно как plus и minus соответственно. В некоторых контекстах выбор этого назначения (то есть, какой диапазон значений считается положительным, а какой отрицательным) является естественным, тогда как в других контекстах выбор произволен, что делает необходимым явное соглашение о знаках, единственным требованием является последовательное использование соглашения.

Во многих контекстах принято ассоциировать знак с мерой угла , в частности, ориентированного угла или угла поворота . В такой ситуации знак указывает, находится ли угол в направлении по часовой стрелке или против часовой стрелки. Хотя могут использоваться различные соглашения, в математике принято считать углы против часовой стрелки положительными, а углы по часовой стрелке — отрицательными. [4]
Также возможно связать знак с углом поворота в трех измерениях, предполагая, что ось поворота ориентирована. В частности, правостороннее вращение вокруг ориентированной оси обычно считается положительным, а левостороннее — отрицательным.
Угол, который является отрицательным по отношению к данному углу, имеет равную дугу, но противоположную ось . [5]
Когда величина x изменяется с течением времени, изменение значения x обычно определяется уравнением
Используя это соглашение, увеличение x считается положительным изменением, а уменьшение x считается отрицательным изменением. В исчислении это же соглашение используется в определении производной . В результате любая возрастающая функция имеет положительную производную, в то время как любая убывающая функция имеет отрицательную производную.
При изучении одномерных перемещений и движений в аналитической геометрии и физике принято обозначать два возможных направления как положительное и отрицательное. Поскольку числовая прямая обычно рисуется с положительными числами справа и отрицательными числами слева, общепринятым соглашением является то, что движениям вправо присваивается положительный знак, а движениям влево — отрицательный знак.
На декартовой плоскости направления вправо и вверх обычно считаются положительными, причем вправо — это положительное направление x , а вверх — положительное направление y . Если вектор смещения разделить на его векторные компоненты , то горизонтальная часть будет положительной для движения вправо и отрицательной для движения влево, тогда как вертикальная часть будет положительной для движения вверх и отрицательной для движения вниз.
Аналогично, отрицательная скорость (скорость изменения смещения) подразумевает скорость в противоположном направлении , т. е. удаление вместо продвижения; особым случаем является радиальная скорость .
В трехмерном пространстве понятия, связанные со знаком, можно обнаружить в двух нормальных ориентациях и ориентируемости в целом.
В вычислениях целочисленное значение может быть как со знаком, так и без знака, в зависимости от того, отслеживает ли компьютер знак числа. Ограничивая целочисленную переменную только неотрицательными значениями, можно использовать еще один бит для хранения значения числа. Из-за способа, которым целочисленная арифметика выполняется в компьютерах, представления знаковых чисел обычно не хранят знак как один независимый бит, вместо этого используя, например, дополнение до двух .
Напротив, действительные числа хранятся и обрабатываются как значения с плавающей точкой . Значения с плавающей точкой представлены с использованием трех отдельных значений: мантиссы, экспоненты и знака. Учитывая этот отдельный бит знака, можно представить как положительный, так и отрицательный ноль. Большинство языков программирования обычно рассматривают положительный ноль и отрицательный ноль как эквивалентные значения, хотя они предоставляют средства, с помощью которых можно обнаружить различие.
Помимо знака действительного числа, слово «знак» также используется в различных связанных с ним значениях в математике и других науках: