В науке процесс , который необратим , называется необратимым . Это понятие часто возникает в термодинамике . Все сложные естественные процессы необратимы, [1] [2] [3] [4] хотя фазовый переход при температуре сосуществования (например, таяние кубиков льда в воде) хорошо аппроксимируется как обратимый.
В термодинамике изменение термодинамического состояния системы и всего ее окружения не может быть точно восстановлено до его начального состояния путем бесконечно малых изменений некоторого свойства системы без затрат энергии. Система, которая подвергается необратимому процессу, все еще может вернуться в свое начальное состояние. Поскольку энтропия является функцией состояния , изменение энтропии системы одинаково, является ли процесс обратимым или необратимым. Однако невозможность возникает при восстановлении среды до ее собственных начальных условий. Необратимый процесс увеличивает общую энтропию системы и ее окружения. Второй закон термодинамики может быть использован для определения того, является ли гипотетический процесс обратимым или нет.
Интуитивно, процесс обратим, если нет диссипации . Например, расширение Джоуля необратимо, потому что изначально система неоднородна. Изначально есть часть системы с газом и часть системы без газа. Для того, чтобы произошло диссипация, должна быть такая неоднородность. Это то же самое, как если бы в системе одна часть газа была горячей, а другая холодной. Тогда произойдет диссипация; распределение температуры станет равномерным без выполнения работы, и это будет необратимо, потому что вы не сможете добавить или удалить тепло или изменить объем, чтобы вернуть систему в исходное состояние. Таким образом, если система всегда однородна, то процесс обратим, то есть вы можете вернуть систему в исходное состояние, либо добавив или убрав тепло, выполнив работу над системой, либо позволив системе выполнить работу. В качестве другого примера, чтобы аппроксимировать расширение в двигателе внутреннего сгорания как обратимое, мы предположим, что температура и давление равномерно изменяются по всему объему после искры. Очевидно, что это не так, и есть фронт пламени , а иногда даже детонация двигателя . Одна из причин, по которой дизельные двигатели способны достигать более высокой эффективности, заключается в том, что сгорание происходит гораздо более равномерно, поэтому меньше энергии теряется на рассеивание, и процесс ближе к обратимому. [ необходима цитата ]
Явление необратимости возникает из-за того, что если термодинамическая система , которая является любой системой достаточной сложности, взаимодействующих молекул, переводится из одного термодинамического состояния в другое, конфигурация или расположение атомов и молекул в системе изменятся непредсказуемым образом. [5] [6] Некоторая «энергия преобразования» будет использоваться, поскольку молекулы «рабочего тела» выполняют работу друг над другом, когда они переходят из одного состояния в другое. Во время этого преобразования будет происходить некоторая потеря или рассеивание тепловой энергии из-за межмолекулярного трения и столкновений. Эта энергия не будет восстановлена, если процесс будет обращен вспять.
Многие биологические процессы, которые когда-то считались обратимыми, на самом деле оказались парой двух необратимых процессов. В то время как когда-то считалось, что один фермент катализирует как прямые, так и обратные химические изменения, исследования показали, что для выполнения того, что приводит к паре термодинамически необратимых процессов, обычно требуются два отдельных фермента схожей структуры. [7]
Термодинамика определяет статистическое поведение большого числа сущностей, точное поведение которых задается более конкретными законами. В то время как все фундаментальные теоретические законы физики обратимы во времени, [8] экспериментально вероятность реальной обратимости низка, и прежнее состояние системы и окружения восстанавливается только в определенной степени (см.: принцип неопределенности ). Обратимость термодинамики должна быть статистической по своей природе; то есть должно быть просто крайне маловероятно, но не невозможно, что система понизит энтропию. Другими словами, обратимость во времени выполняется, если процесс происходит таким же образом, если бы время текло в обратном направлении или порядок состояний в процессе был бы обратным (последнее состояние становится первым и наоборот).
Немецкий физик Рудольф Клаузиус в 1850-х годах был первым, кто математически количественно оценил открытие необратимости в природе, введя понятие энтропии . В своих мемуарах 1854 года «О модифицированной форме второй фундаментальной теоремы в механической теории тепла» Клаузиус утверждает:
Более того, может случиться, что вместо нисходящей передачи тепла, сопровождающей в одном и том же процессе восходящую передачу, может произойти другое постоянное изменение, особенностью которого является то, что оно необратимо, не заменяясь новым постоянным изменением подобного рода или не вызывая нисходящей передачи тепла.
Проще говоря, Клаузиус утверждает, что система не может передавать тепло от более холодного тела к более горячему. Например, чашка горячего кофе, помещенная в область с комнатной температурой (~72 °F), будет передавать тепло в окружающую среду и, таким образом, охлаждаться, при этом температура в комнате немного повышается (до ~72,3 °F ). Однако та же самая начальная чашка кофе никогда не будет поглощать тепло из окружающей среды, заставляя себя становиться еще горячее, при этом температура в комнате понижается (до ~71,7 °F ). Поэтому процесс охлаждения кофе необратим, если в систему не будет добавлена дополнительная энергия.
Однако при попытке примирить микроанализ системы с наблюдениями за ее макросостоянием возник парадокс. Многие процессы математически обратимы в своем микросостоянии при анализе с использованием классической ньютоновской механики. Этот парадокс явно портит микроскопические объяснения макроскопической тенденции к равновесию, такие как аргумент Джеймса Клерка Максвелла 1860 года о том, что молекулярные столкновения влекут за собой выравнивание температур смешанных газов. [9] С 1872 по 1875 год Людвиг Больцман усилил статистическое объяснение этого парадокса в форме формулы энтропии Больцмана , заявив, что увеличение числа возможных микросостояний, в которых может находиться система, увеличит энтропию системы, что сделает менее вероятным возврат системы в более раннее состояние. Его формулы количественно описали анализ, проведенный Уильямом Томсоном, 1-м бароном Кельвином , который утверждал, что: [10] [11]
Уравнения движения в абстрактной динамике совершенно обратимы; любое решение этих уравнений остается справедливым, если заменить переменную времени t на –t. С другой стороны, физические процессы необратимы: например, трение твердых тел, теплопроводность и диффузия. Тем не менее, принцип рассеивания энергии совместим с молекулярной теорией, в которой каждая частица подчиняется законам абстрактной динамики.
Другое объяснение необратимых систем было представлено французским математиком Анри Пуанкаре . В 1890 году он опубликовал свое первое объяснение нелинейной динамики, также называемое теорией хаоса . Применяя теорию хаоса ко второму закону термодинамики , парадокс необратимости можно объяснить ошибками, связанными с масштабированием от микросостояний к макросостояниям и степенями свободы, используемыми при проведении экспериментальных наблюдений. Чувствительность к начальным условиям, относящимся к системе и ее окружению в соединениях микросостояний, в проявление необратимых характеристик в наблюдаемой физической сфере. [12]
В физической сфере присутствует множество необратимых процессов, к которым можно отнести невозможность достижения 100% эффективности в передаче энергии. Ниже приведен список спонтанных событий, которые способствуют необратимости процессов. [13]
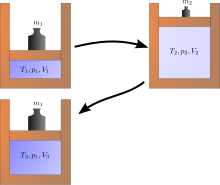
Джоулево расширение является примером классической термодинамики, поскольку легко вычислить результирующее увеличение энтропии. Оно происходит, когда объем газа удерживается в одной стороне термически изолированного контейнера (через небольшую перегородку), а другая сторона контейнера вакуумируется; затем перегородка между двумя частями контейнера открывается, и газ заполняет весь контейнер. Внутренняя энергия газа остается прежней, в то время как объем увеличивается. Исходное состояние не может быть восстановлено простым сжатием газа до его исходного объема, поскольку внутренняя энергия будет увеличена этим сжатием. Исходное состояние может быть восстановлено только путем последующего охлаждения повторно сжатой системы и, таким образом, необратимого нагрева окружающей среды. Диаграмма справа применима только в том случае, если первое расширение является «свободным» (джоулево расширение), т. е. не может быть никакого атмосферного давления снаружи цилиндра и никакого поднятого веса.
Разница между обратимыми и необратимыми событиями имеет особую объяснительную ценность в сложных системах (таких как живые организмы или экосистемы ). По словам биологов Умберто Матураны и Франциско Варелы , живые организмы характеризуются аутопоэзисом , который обеспечивает их дальнейшее существование. Более примитивные формы самоорганизующихся систем были описаны физиком и химиком Ильей Пригожиным . В контексте сложных систем события, которые приводят к завершению определенных процессов самоорганизации , таких как смерть , вымирание вида или крах метеорологической системы, можно считать необратимыми. Даже если бы клон с тем же организационным принципом (например, идентичная структура ДНК) мог бы быть разработан, это не означало бы, что прежняя особая система возвращается к существованию. События, к которым могут адаптироваться самоорганизующиеся способности организмов, видов или других сложных систем, такие как незначительные травмы или изменения в физической среде, являются обратимыми. Однако адаптация зависит от импорта негэнтропии в организм, тем самым увеличивая необратимые процессы в его среде. [17] Экологические принципы, такие как принципы устойчивости и принцип предосторожности, можно определить со ссылкой на концепцию обратимости. [18] [19] [20] [21] [22] [23] [5] [24] [25]