Стабильный коллектор

Формализация идеи аттрактора или репеллера в динамических системах

В математике , и в частности в изучении динамических систем , идея устойчивых и неустойчивых множеств или устойчивых и неустойчивых многообразий дает формальное математическое определение общим понятиям, воплощенным в идее аттрактора или репеллера . В случае гиперболической динамики соответствующим понятием является понятие гиперболического множества .

Пример гиперболического потока, иллюстрирующий устойчивые и неустойчивые многообразия. Уравнение векторного поля: . Устойчивое многообразие — это ось x, а неустойчивое многообразие — это другая асимптотическая кривая, пересекающая ось x. ${\displaystyle (x+\exp(-y),-y)}$

Физический пример

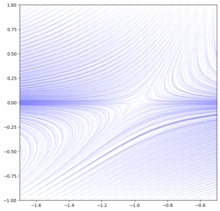
Гравитационные приливные силы, действующие на кольца Сатурна, дают простой для визуализации физический пример. Приливные силы сплющивают кольцо в экваториальной плоскости, даже если они растягивают его в радиальном направлении. Представляя кольца в виде частиц песка или гравия («пыли») на орбите вокруг Сатурна, приливные силы таковы, что любые возмущения, которые толкают частицы выше или ниже экваториальной плоскости, приводят к тому, что эта частица ощущает восстанавливающую силу, толкающую ее обратно в плоскость. Частицы эффективно колеблются в гармоническом колодце, затухающем из-за столкновений. Устойчивое направление перпендикулярно кольцу. Неустойчивое направление — вдоль любого радиуса, где силы растягивают и разъединяют частицы. Две частицы, которые начинают очень близко друг к другу в фазовом пространстве, будут испытывать радиальные силы, заставляющие их расходиться радиально. Эти силы имеют положительный показатель Ляпунова ; траектории лежат на гиперболическом многообразии, а движение частиц по сути хаотично , блуждая по кольцам. Центральный коллектор касается колец, и частицы не испытывают ни сжатия, ни растяжения. Это позволяет гравитационным силам второго порядка доминировать, и поэтому частицы могут увлекаться лунами или луночками в кольцах, синхронизируясь с ними по фазе. Гравитационные силы лун эффективно обеспечивают регулярно повторяющийся небольшой толчок, каждый раз вокруг орбиты, похожий на толчковый ротор , такой как в петле фазовой синхронизации .

Дискретное движение частиц в кольце можно аппроксимировать отображением Пуанкаре . Отображение эффективно предоставляет матрицу переноса системы. Собственный вектор, связанный с наибольшим собственным значением матрицы, — это собственный вектор Фробениуса–Перрона , который также является инвариантной мерой , т.е. фактической плотностью частиц в кольце. Все другие собственные векторы матрицы переноса имеют меньшие собственные значения и соответствуют затухающим модам.

Определение

Ниже приводится определение для случая системы, которая является либо итерационной функцией , либо имеет динамику дискретного времени. Аналогичные понятия применимы к системам, эволюция времени которых задается потоком .

Пусть будет топологическим пространством , а гомеоморфизмом . Если — неподвижная точка для , то устойчивое множество определяется соотношением ${\displaystyle X}$ ${\displaystyle f\colon X\to X}$ ${\displaystyle p}$ ${\displaystyle f}$ ${\displaystyle p}$

${\displaystyle W^{s}(f,p)=\{q\in X:f^{n}(q)\to p{\mbox{ as }}n\to \infty \}}$

и нестабильный набор ${\displaystyle p}$ определяется как

${\displaystyle W^{u}(f,p)=\{q\in X:f^{-n}(q)\to p{\mbox{ as }}n\to \infty \}.}$

Здесь обозначает обратную функцию функции , т.е. , где — тождественное отображение на . ${\displaystyle f^{-1}}$ ${\displaystyle f}$ ${\displaystyle f\circ f^{-1}=f^{-1}\circ f=id_{X}}$ ${\displaystyle id_{X}}$ ${\displaystyle X}$

Если — периодическая точка наименьшего периода , то она является неподвижной точкой , а устойчивые и неустойчивые множества определяются соотношением ${\displaystyle p}$ ${\displaystyle k}$ ${\displaystyle f^{k}}$ ${\displaystyle p}$

${\displaystyle W^{s}(f,p)=W^{s}(f^{k},p)}$

и

${\displaystyle W^{u}(f,p)=W^{u}(f^{k},p).}$

При наличии окрестности локальные устойчивые и неустойчивые множества определяются как ${\displaystyle U}$ ${\displaystyle p}$ ${\displaystyle p}$

${\displaystyle W_{\mathrm {loc} }^{s}(f,p,U)=\{q\in U:f^{n}(q)\in U{\mbox{ for each }}n\geq 0\}}$

и

${\displaystyle W_{\mathrm {loc} }^{u}(f,p,U)=W_{\mathrm {loc} }^{s}(f^{-1},p,U).}$

Если метризуемо , то мы можем определить устойчивые и неустойчивые множества для любой точки с помощью ${\displaystyle X}$

${\displaystyle W^{s}(f,p)=\{q\in X:d(f^{n}(q),f^{n}(p))\to 0{\mbox{ for }}n\to \infty \}}$

и

${\displaystyle W^{u}(f,p)=W^{s}(f^{-1},p),}$

где — метрика для . Это определение, очевидно, совпадает с предыдущим, когда — периодическая точка. ${\displaystyle d}$ ${\displaystyle X}$ ${\displaystyle p}$

Предположим теперь, что — компактное гладкое многообразие , и — диффеоморфизм , . Если — гиперболическая периодическая точка, теорема об устойчивом многообразии гарантирует, что для некоторой окрестности локальные устойчивое и неустойчивое множества являются вложенными дисками, касательными пространствами которых в являются и (устойчивое и неустойчивое пространства ), соответственно; более того, они непрерывно (в определенном смысле) изменяются в окрестности в топологии (пространство всех диффеоморфизмов из в себя). Наконец, устойчивое и неустойчивое множества являются инъективно погруженными дисками. Вот почему их обычно называют устойчивыми и неустойчивыми многообразиями . Этот результат также верен для непериодических точек, пока они лежат в некотором гиперболическом множестве (теорема об устойчивом многообразии для гиперболических множеств). ${\displaystyle X}$ ${\displaystyle f}$ ${\displaystyle {\mathcal {C}}^{k}}$ ${\displaystyle k\geq 1}$ ${\displaystyle p}$ ${\displaystyle U}$ ${\displaystyle p}$ ${\displaystyle {\mathcal {C}}^{k}}$ ${\displaystyle p}$ ${\displaystyle E^{s}}$ ${\displaystyle E^{u}}$ ${\displaystyle Df(p)}$ ${\displaystyle f}$ ${\displaystyle {\mathcal {C}}^{k}}$ ${\displaystyle \mathrm {Diff} ^{k}(X)}$ ${\displaystyle {\mathcal {C}}^{k}}$ ${\displaystyle X}$ ${\displaystyle {\mathcal {C}}^{k}}$

Замечание

Если — (конечномерное) векторное пространство и изоморфизм, то его устойчивое и неустойчивое множества называются устойчивым пространством и неустойчивым пространством соответственно. ${\displaystyle X}$ ${\displaystyle f}$

Смотрите также

• Инвариантное многообразие
• Центральный коллектор
• Установлен предел
• Джулия сет
• Медленный коллектор
• Инерционный коллектор
• Нормально гиперболическое инвариантное многообразие
• Лагранжева когерентная структура

Ссылки

• Авраам, Ральф; Марсден, Джерролд Э. (1978). Основы механики . Reading Mass.: Benjamin/Cummings. ISBN 0-8053-0102-X.
• Ирвин, Майкл С. (2001). «Стабильные многообразия». Гладкие динамические системы . World Scientific. стр. 143–160. ISBN 981-02-4599-8.
• Шритаран, СС (1990). Теория инвариантных многообразий для гидродинамического перехода . Нью-Йорк: John Wiley & Sons. ISBN 0-582-06781-2.

В данной статье использованы материалы из Stable multiple на PlanetMath , лицензированные по лицензии Creative Commons Attribution/Share-Alike License .