Овал Кассини

Класс плоских кривых четвертой степени

Три овала Кассини, различающиеся диапазоном значений параметра e (равного b / a ):

  0 < е < 1

  е = 1

  1 < е < √ 2

Не показано: e ≥ √ 2 (выпуклый).

В геометрии овал Кассини — это плоская кривая четвертой степени, определяемая как геометрическое место точек на плоскости, такое, что произведение расстояний до двух фиксированных точек ( фокусов ) является постоянным. Это можно сравнить с эллипсом , для которого постоянна сумма расстояний, а не произведение. Овалы Кассини являются особым случаем полиномиальных лемнискат , когда используемый полином имеет степень 2.

Овалы Кассини названы в честь астронома Джованни Доменико Кассини, который изучал их в конце 17 века. ^[1] Кассини считал, что планета, вращающаяся вокруг другого тела, движется по одному из этих овалов, при этом тело, вокруг которого она вращается, находится в одном из фокусов овала. ^[2] Другие названия включают овалы Кассини , кривые Кассини и овалы Кассини .

Формальное определение

Овал Кассини: для любого местоположения P на кривой ${\displaystyle |PP_{1}|\!\!\;\times \!\!\;|PP_{2}|=b^{2}}$

Овал Кассини — это набор точек, такой, что для любой точки набора произведение расстояний до двух фиксированных точек является константой, обычно записываемой как : ${\displaystyle P}$ ${\displaystyle |PP_{1}|,\,|PP_{2}|}$ ${\displaystyle P_{1},P_{2}}$ ${\displaystyle b^{2}}$ ${\displaystyle b>0}$

${\displaystyle \{P:|PP_{1}|\!\!\;\times \!\!\;|PP_{2}|=b^{2}\}\ .}$

Как и в случае эллипса, неподвижные точки называются фокусами овала Кассини. ${\displaystyle P_{1},P_{2}}$

Уравнения

Если фокусы равны ( a , 0) и (−a , 0), то уравнение кривой имеет вид

${\displaystyle ((x-a)^{2}+y^{2})((x+a)^{2}+y^{2})=b^{4}.}$

При расширении это становится

${\displaystyle (x^{2}+y^{2})^{2}-2a^{2}(x^{2}-y^{2})+a^{4}=b^{4}.}$

Эквивалентное полярное уравнение имеет вид

${\displaystyle r^{4}-2a^{2}r^{2}\cos 2\theta =b^{4}-a^{4}.\,}$

Форма

Некоторые овалы Кассини. ( b  =  0,6 a , 0,8 a , a , 1,2 a , 1,4 a , 1,6 a )

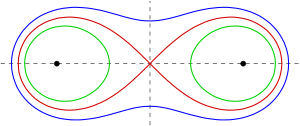
Кривая зависит, с точностью до подобия, от e = b / a . При e < 1 кривая состоит из двух разъединенных петель, каждая из которых содержит фокус. При e = 1 кривая является лемнискатой Бернулли, имеющей форму боковой восьмерки с двойной точкой (в частности, крунодой ) в начале координат. ^{[3] [4]} При e > 1 кривая является одной связанной петлей, охватывающей оба фокуса. Она имеет форму арахиса при и выпукла при ^[5] Предельным случаем a → 0 (следовательно, e → ∞ ), в котором фокусы совпадают друг с другом, является окружность . ${\displaystyle 1<e<{\sqrt {2}}}$ ${\displaystyle e\geq {\sqrt {2}}\,.}$

Кривая всегда имеет x -пересечения в ±  c , где c ² = a ² + b ² . Когда e < 1, есть два дополнительных действительных x -пересечения, а когда e > 1, есть два действительных y -пересечения, все остальные x - и y -пересечения являются мнимыми. ^[6]

Кривая имеет двойные точки в круговых точках на бесконечности , другими словами, кривая является бициркулярной . Эти точки являются бифлекнодами, что означает, что кривая имеет две различные касательные в этих точках, и каждая ветвь кривой имеет там точку перегиба. Из этой информации и формул Плюккера можно вывести числа Плюккера для случая e ≠ 1 : степень = 4, класс = 8, количество узлов = 2, количество точек возврата = 0, количество двойных касательных = 8, количество точек перегиба = 12, род = 1. ^[7]

Касательные в точках окружности задаются как x ± iy = ±  a , которые имеют действительные точки пересечения в (±  a , 0) . Таким образом, фокусы, по сути, являются фокусами в смысле, определенном Плюккером. ^[8] Круговые точки являются точками перегиба, поэтому они являются тройными фокусами. Когда e ≠ 1, кривая имеет класс восемь, что подразумевает, что должно быть всего восемь действительных фокусов. Шесть из них были учтены в двух тройных фокусах, а оставшиеся два находятся в Таким образом, дополнительные фокусы находятся на оси x , когда кривая имеет две петли, и на оси y , когда кривая имеет одну петлю. ^[9] $${\displaystyle {\begin{aligned}\left(\pm a{\sqrt {1-e^{4}}},0\right)&\quad (e<1),\\\left(0,\pm a{\sqrt {e^{4}-1}}\right)&\quad (e>1).\end{aligned}}}$$

Овалы Кассини и ортогональные траектории

Овалы Кассини и их ортогональные траектории (гиперболы)

Ортогональные траектории данного пучка кривых — это кривые, которые пересекают все данные кривые ортогонально. Например, ортогональные траектории пучка софокусных эллипсов — это софокусные гиперболы с теми же фокусами. Для овалов Кассини имеем:

• Ортогональные траектории кривых Кассини с фокусами представляют собой равносторонние гиперболы, содержащие тот же центр, что и овалы Кассини (см. рисунок). ${\displaystyle P_{1},P_{2}}$ ${\displaystyle P_{1},P_{2}}$

Доказательство:
Для простоты выбираем . ${\displaystyle P_{1}=(1,0),\,P_{2}=(-1,0)}$

Овалы Кассини имеют уравнение $${\displaystyle f(x,y)=(x^{2}+y^{2})^{2}-2(x^{2}-y^{2})+1-b^{4}=0.}$$

Равносторонние гиперболы ( их асимптоты прямоугольные), содержащие с центром, можно описать уравнением ${\displaystyle (1,0),(-1,0)}$ ${\displaystyle (0,0)}$ $${\displaystyle x^{2}-y^{2}-\lambda xy-1=0,\ \ \ \lambda \in \mathbb {R} .}$$

Эти конические сечения не имеют общих точек с осью y и пересекают ось x в точке . Их дискриминанты показывают, что эти кривые являются гиперболами. Более детальное исследование показывает, что гиперболы являются прямоугольными. Для получения нормалей, которые не зависят от параметра, более удобным является следующее неявное представление Простой расчет показывает, что для всех . Следовательно, овалы Кассини и гиперболы пересекаются ортогонально. ${\displaystyle (\pm 1,0)}$ ${\displaystyle \lambda }$ $${\displaystyle g(x,y)={\frac {x^{2}-y^{2}-1}{xy}}-\lambda ={\frac {x}{y}}-{\frac {y}{x}}-{\frac {1}{xy}}-\lambda =0\;.}$$ ${\displaystyle \operatorname {grad} f(x,y)\cdot \operatorname {grad} g(x,y)=0}$ ${\displaystyle (x,y),\,x\neq 0\neq y}$

Замечание:
Изображение, изображающее овалы Кассини и гиперболы, выглядит как эквипотенциальные кривые двух равных точечных зарядов вместе с линиями генерируемого электрического поля . Но для потенциала двух равных точечных зарядов имеем . (См. Неявная кривая .) Вместо этого эти кривые на самом деле соответствуют (плоским сечениям) эквипотенциальных множеств двух бесконечных проводов с одинаковой постоянной плотностью линейного заряда или, альтернативно, множествам уровня сумм функций Грина для лапласиана в двух измерениях с центрами в фокусах. ${\displaystyle 1/|PP_{1}|+1/|PP_{2}|={\text{constant}}}$

Однопетлевые и двухпетлевые кривые Кассини можно представить как ортогональные траектории друг друга, когда каждое семейство является коаксиальным, но не конфокальным. Если однопетлевые описываются , то фокусы являются переменными на оси , если , если ; если двухпетлевые описываются , то оси, соответственно, и . Каждая кривая, с точностью до подобия, появляется дважды на изображении, которое теперь напоминает линии поля и потенциальные кривые для четырех равных точечных зарядов, расположенных в и . Кроме того, часть этого изображения в верхней полуплоскости изображает следующую ситуацию: Двойные петли представляют собой сокращенный набор классов конгруэнтности для центральных коник Штейнера в гиперболической плоскости, полученных прямыми коллинеациями; ^[10] и каждая однопетлевая является геометрическим местом точек, таким образом, что угол постоянен, где и является основанием перпендикуляра, проходящего через линию, описанную . ${\displaystyle (x^{2}+y^{2})-1=axy}$ ${\displaystyle y=x}$ ${\displaystyle a>0}$ ${\displaystyle y=-x}$ ${\displaystyle a<0}$ ${\displaystyle (x^{2}+y^{2})+1=b(x^{2}-y^{2})}$ ${\displaystyle y=0}$ ${\displaystyle x=0}$ ${\displaystyle (\pm 1,0)}$ ${\displaystyle (0,\pm 1)}$ ${\displaystyle P}$ ${\displaystyle OPQ}$ ${\displaystyle O=(0,1)}$ ${\displaystyle Q}$ ${\displaystyle P}$ ${\displaystyle x^{2}+y^{2}=1}$

Примеры

Вторая лемниската множества Мандельброта представляет собой овал Кассини, определяемый уравнением Его фокусы находятся в точках c на комплексной плоскости , имеющих орбиты, где каждое второе значение z равно нулю, т.е. значениям 0 и −1. ${\displaystyle L_{2}=\{c:\operatorname {abs} (c^{2}+c)=ER\}.}$

Овалы Кассини на торах

Овалы Кассини как плоские сечения тора (тор справа — веретенообразный тор )

Овалы Кассини выглядят как плоские сечения торов , но только тогда, когда секущая плоскость параллельна оси тора, а ее расстояние до оси равно радиусу образующей окружности (см. рисунок).

Пересечение тора с уравнением

${\displaystyle \left(x^{2}+y^{2}+z^{2}+R^{2}-r^{2}\right)^{2}=4R^{2}\!\left(x^{2}+y^{2}\right)}$

и самолет дает ${\displaystyle y=r}$

${\displaystyle \left(x^{2}+z^{2}+R^{2}\right)^{2}=4R^{2}\!\left(x^{2}+r^{2}\right).}$

После частичного решения первой скобки получаем уравнение

${\displaystyle \left(x^{2}+z^{2}\right)^{2}-2R^{2}(x^{2}-z^{2})=4R^{2}r^{2}-R^{4},}$

которое представляет собой уравнение овала Кассини с параметрами и . ${\displaystyle b^{2}=2Rr}$ ${\displaystyle a=R}$

Обобщения

Метод Кассини легко обобщить на кривые и поверхности с произвольным числом определяющих точек:

• ${\displaystyle |PP_{1}|\times |PP_{2}|\times \cdots \times |PP_{n}|=b^{n}}$

описывает в плоском случае неявную кривую , а в трехмерном пространстве — неявную поверхность .

• 
  кривая с 3 определяющими точками
• 
  поверхность с 6 определяющими точками

Смотрите также

• Двухцентровые биполярные координаты

Ссылки

1. Кассини
2. Коэн 1962.
3. Бассет стр. 163
4. Лоуден
5. «Овал Кассини — Энциклопедия математики».
6. Бассет стр. 163
7. Бассет стр. 163
8. См. Бассет, стр. 47.
9. Бассет стр. 164
10. Сарли, Джон (апрель 2012 г.). «Конические сечения в гиперболической плоскости, присущие группе коллинеаций». Журнал геометрии . 103 (1): 131–148. doi :10.1007/s00022-012-0115-5. ISSN  0047-2468. S2CID  253597755.

Библиография

• Ж.-Д. Кассини (1693 г.). De l'Origine et du progrès de l'astronomie и сын использования в географии и навигации. L'Imprimerie Royale. стр. 36.
• Коэн, И. Бернар (1962). «Лейбниц об эллиптических орбитах: как видно из его переписки с Королевской академией наук в 1700 году». Журнал истории медицины и смежных наук . 17 (1): 72–82. doi :10.1093/jhmas/xvii.1.72. JSTOR  24620858.
• J. Dennis Lawrence (1972). Каталог специальных плоских кривых . Dover Publications . стр. 5, 153–155. ISBN 0-486-60288-5.
• AB Basset (1901). Элементарный трактат о кубических и четвертых кривых. Лондон: Deighton Bell and Co., стр. 162 и далее.
• Лоуден, Д.Ф., «Семейства овалов и их ортогональные траектории», Mathematical Gazette 83, ноябрь 1999 г., 410–420.

Внешние ссылки

• «Овал Кассини». Энциклопедия математики . EMS Press . 2001 [1994].
• Описание MacTutor
• Вайсштейн, Эрик В. «Овалы Кассини». MathWorld .
• Описание 2Dcurves.com
• «История математики Мактьютора» Знаменитые кривые