Конверт (математика)

Семейство кривых в геометрии

Построение оболочки семейства кривых.

В геометрии оболочка плоского семейства кривых — это кривая , которая касается каждого члена семейства в некоторой точке, и эти точки касания вместе образуют всю оболочку. Классически точку на огибающей можно рассматривать как пересечение двух « бесконечно мало смежных» кривых, что означает предел пересечений соседних кривых. Эту идею можно обобщить на оболочку поверхностей в пространстве и так далее на более высокие измерения.

Чтобы иметь огибающую, необходимо, чтобы отдельные члены семейства кривых были дифференцируемыми кривыми , поскольку в противном случае концепция касания не применяется, и между членами должен происходить плавный переход. Но этих условий недостаточно – у данной семьи может не оказаться конверта. Простой пример этому дает семейство концентрических кругов расширяющегося радиуса.

Конверт семейства кривых

Пусть каждая кривая C _t в семействе задана как решение уравнения f _t ( x ,  y )=0 (см. неявную кривую ), где t — параметр. Запишите F ( t ,  x ,  y ) = ft ( x ,  y ) и предположим, _что F дифференцируемо.

Тогда оболочка семейства Ct определяется как набор точек ( x, y ₎ , для которых одновременно ${\displaystyle {\mathcal {D}}}$

${\displaystyle F(t,x,y)=0~~{\mathsf {and}}~~{\partial F \over \partial t}(t,x,y)=0}$

для некоторого значения t , где – частная производная F по t . ^[1] ${\displaystyle \partial F/\partial t}$

Если t и u , t ≠ u — два значения параметра, то пересечение кривых C _t и C _u определяется выражением

${\displaystyle F(t,x,y)=F(u,x,y)=0\,}$

или, что то же самое,

${\displaystyle F(t,x,y)=0~~{\mathsf {and}}~~{\frac {F(u,x,y)-F(t,x,y)}{u-t}}=0.}$

Полагая, что u → t, получим определение, приведенное выше.

Важный частный случай — когда F ( t ,  x ,  y ) является многочленом от t . Это включает в себя, путем очистки знаменателей , случай, когда F ( t ,  x ,  y ) является рациональной функцией от t . В этом случае определение сводится к тому, что t является двойным корнем из F ( t ,  x ,  y ), поэтому уравнение огибающей можно найти, установив дискриминант F равным 0 (поскольку определение требует F = 0 в некоторой точке) . t и первая производная = 0, т. е. ее значение 0 и это мин/макс при этом t).

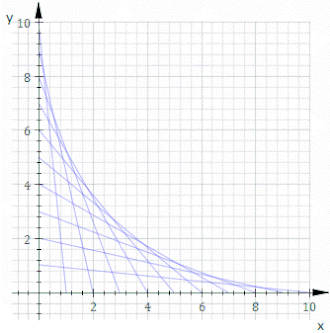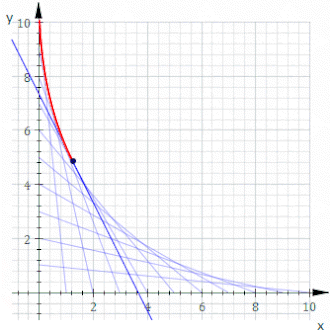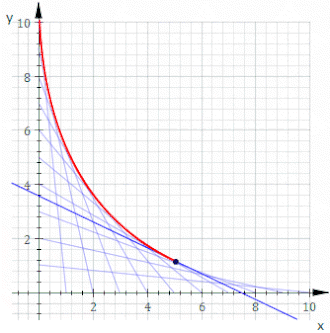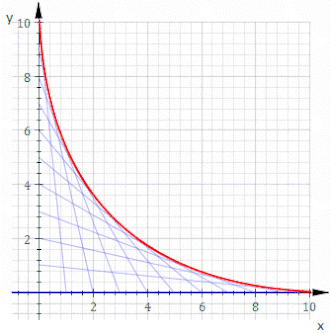
Например, пусть C _t будет линией, точки пересечения x и y равны t и 11− t , это показано на анимации выше. Уравнение C _t имеет вид

${\displaystyle {\frac {x}{t}}+{\frac {y}{11-t}}=1}$

или, очищая дроби,

${\displaystyle x(11-t)+yt-t(11-t)=t^{2}+(-x+y-11)t+11x=0.\,}$

Тогда уравнение оболочки имеет вид

${\displaystyle (-x+y-11)^{2}-44x=(x-y)^{2}-22(x+y)+121=0.\,}$

Часто, когда F не является рациональной функцией параметра, его можно свести к этому случаю соответствующей заменой. Например, если семейство задано C _θ с уравнением вида u ( x ,  y )cos θ+ v ( x ,  y )sin θ = w ( x ,  y ), то полагая t = e ^{i θ} , cos θ=( t +1/ t )/2, sin θ=( t -1/ t )/2 я меняю уравнение кривой на

${\displaystyle u{1 \over 2}(t+{1 \over t})+v{1 \over 2i}(t-{1 \over t})=w}$

или

${\displaystyle (u-iv)t^{2}-2wt+(u+iv)=0.\,}$

Уравнение огибающей затем задается путем установки дискриминанта на 0:

${\displaystyle (u-iv)(u+iv)-w^{2}=0\,}$

или

${\displaystyle u^{2}+v^{2}=w^{2}.\,}$

Альтернативные определения

1. Огибающая E ₁ является пределом пересечений соседних кривых C _t .
2. Огибающая E ₂ представляет собой кривую, касающуюся всех C _t .
3. Огибающая E ₃ является границей области, заполненной кривыми C _t .

Затем , и , где — набор точек, определенный в начале родительского раздела этого подраздела. ${\displaystyle E_{1}\subseteq {\mathcal {D}}}$ ${\displaystyle E_{2}\subseteq {\mathcal {D}}}$ ${\displaystyle E_{3}\subseteq {\mathcal {D}}}$ ${\displaystyle {\mathcal {D}}}$

Примеры

Пример 1

Эти определения E ₁ , E ₂ и E ₃ оболочки могут представлять собой разные наборы. Рассмотрим, например, кривую y = x ³ , параметризованную γ: R → R ² , где γ( t ) = ( t , t ³ ) . Однопараметрическое семейство кривых будет задано касательными к γ.

Сначала вычислим дискриминант . Производящая функция ${\displaystyle {\mathcal {D}}}$

${\displaystyle F(t,(x,y))=3t^{2}x-y-2t^{3}.}$

Вычисление частной производной F _t знак равно 6 t ( x – t ) . Отсюда следует, что либо x = t , либо t = 0 . Сначала предположим, что x = t и t ≠ 0 . Подставляя в F: и так, предполагая, что t ≠ 0, следует, что F = F _t = 0 тогда и только тогда, когда ( x , y ) = ( t , t ³ ) . Далее, предполагая, что t = 0 , и подстановка в F дает F (0,( x , y )) = − y . Итак, предполагая t = 0 , отсюда следует, что F = F _t = 0 тогда и только тогда, когда y = 0 . Таким образом, дискриминант — это исходная кривая и ее касательная в точке γ(0): ${\displaystyle F(t,(t,y))=t^{3}-y\,}$

${\displaystyle {\mathcal {D}}=\{(x,y)\in \mathbb {R} ^{2}:y=x^{3}\}\cup \{(x,y)\in \mathbb {R} ^{2}:y=0\}\ .}$

Далее мы вычисляем E ₁ . Одна кривая задается как F ( t ,( x , y )) = 0 , а соседняя кривая задается F ( t + ε,( x , y )) , где ε — некоторое очень маленькое число. Точка пересечения возникает в результате рассмотрения предела F ( t ,( x , y )) =  F ( t + ε,( x , y )) , когда ε стремится к нулю. Обратите внимание, что F ( t ,( x , y )) =  F ( t + ε,( x , y )) тогда и только тогда, когда

${\displaystyle L:=F(t,(x,y))-F(t+\varepsilon ,(x,y))=2\varepsilon ^{3}+6\varepsilon t^{2}+6\varepsilon ^{2}t-(3\varepsilon ^{2}+6\varepsilon t)x=0.}$

Если t ≠ 0 , то L имеет только один множитель ε. Если предположить, что t ≠ 0 , то пересечение определяется выражением

${\displaystyle \lim _{\varepsilon \to 0}{\frac {1}{\varepsilon }}L=6t(t-x)\ .}$

Поскольку t ≠ 0, отсюда следует, что x = t . Значение y вычисляется, зная, что эта точка должна лежать на касательной к исходной кривой γ: F ( t ,( x , y )) = 0 . Подстановка и решение дает y = t ³ . Когда t = 0 , L делится на ε ² . Предполагая, что t = 0 , тогда пересечение определяется выражением

${\displaystyle \lim _{\varepsilon \to 0}{\frac {1}{\varepsilon ^{2}}}L=3x\ .}$

Отсюда следует, что x = 0 , и зная, что F ( t ,( x , y )) = 0 , получаем y = 0 . Следует, что

${\displaystyle E_{1}=\{(x,y)\in \mathbb {R} ^{2}:y=x^{3}\}\ .}$

Далее мы вычисляем E ₂ . Сама кривая — это кривая, касающаяся всех своих касательных линий. Следует, что

${\displaystyle E_{2}=\{(x,y)\in \mathbb {R} ^{2}:y=x^{3}\}\ .}$

Наконец, мы вычисляем E ₃ . Через каждую точку плоскости проходит хотя бы одна касательная к γ, поэтому область, заполненная касательными линиями, представляет собой всю плоскость. Поэтому граница E ₃ представляет собой пустое множество. Действительно, рассмотрим точку на плоскости, скажем ( x ₀ , y ₀ ). Эта точка лежит на касательной тогда и только тогда, когда существует t такое , что

${\displaystyle F(t,(x_{0},y_{0}))=3t^{2}x_{0}-y_{0}-2t^{3}=0\ .}$

Это кубика по t и поэтому имеет хотя бы одно вещественное решение. Отсюда следует, что хотя бы одна касательная к γ должна проходить через любую данную точку плоскости. Если y > x ³ и y > 0 , то каждая точка ( x , y ) имеет ровно одну касательную к γ, проходящую через нее. То же самое верно, если y < x ³ y < 0 . Если y < x ³ и y > 0 , то каждая точка ( x , y ) имеет ровно три различные касательные к γ, проходящие через нее. То же самое верно, если y > x ³ и y < 0 . Если y = x ³ и y ≠ 0 , то каждая точка ( x , y ) имеет ровно две касательные к γ, проходящие через нее (это соответствует кубике, имеющей один обычный корень и один повторяющийся корень). То же самое верно, если y ≠ x ³ и y = 0 . Если y = x ³ и x = 0 , т. е. x = y = 0 , то через эту точку проходит единственная касательная к γ (это соответствует кубике, имеющей один действительный корень кратности 3). Следует, что

${\displaystyle E_{3}=\varnothing .}$

Пример 2

Этот график дает огибающую семейства линий, соединяющих точки ( t ,0), (0, k - t ), в которых k принимает значение 1.

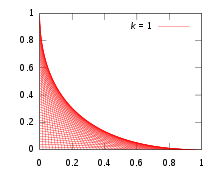
В струнном искусстве принято перекрестно соединять две линии штифтов, расположенных на одинаковом расстоянии друг от друга. Какая кривая образуется?

Для простоты установите штифты по осям x и y ; неортогональный макет — это вращение и масштабирование . Общая прямая нить соединяет две точки (0, k - t ) и ( t , 0), где k — произвольная константа масштабирования, а семейство линий генерируется путем изменения параметра t . Из простой геометрии уравнение этой прямой линии имеет вид y = −( k  −  t ) x / t + k  −  t . Перестановка и приведение в форме F ( x , y , t ) = 0 дает:

Теперь продифференцируйте F ( x , y , t ) по t и приравняйте результат к нулю, чтобы получить

Эти два уравнения совместно определяют уравнение оболочки. Из (2) имеем:

${\displaystyle t={\sqrt {kx}}\,}$

Подстановка этого значения t в (1) и упрощение дает уравнение для конверта:

Или, преобразуя его в более элегантную форму, показывающую симметрию между x и y:

Мы можем выполнить поворот осей, где ось b — это линия y=x, ориентированная на северо-восток, а ось a — это линия y =− x , ориентированная на юго-восток. Эти новые оси связаны с исходными осями xy соотношениями x =( b + a )/ √ 2 и y = ( b − a )/ √ 2 . После подстановки в (4) и разложения и упрощения получим:

что, по-видимому, является уравнением параболы с осью вдоль a = 0 или y = x .

Пример 3

Пусть I ⊂ R — открытый интервал и γ: I → R ² — гладкая плоская кривая, параметризованная длиной дуги . Рассмотрим однопараметрическое семейство нормалей к γ( I ). Линия нормальна к γ в точке γ( t ), если она проходит через γ( t ) и перпендикулярна вектору касательной к γ в точке γ( t ). Пусть T обозначает единичный касательный вектор к γ, а N обозначает единичный вектор нормали . Используя точку для обозначения скалярного произведения , порождающее семейство для однопараметрического семейства нормальных линий задается формулой F  : I × R ² → R , где

${\displaystyle F(t,{\mathbf {x} })=({\mathbf {x} }-\gamma (t))\cdot {\mathbf {T} }(t)\ .}$

Ясно, что ( x − γ)· T = 0 тогда и только тогда, когда x − γ перпендикулярен T или, что то же самое, тогда и только тогда, когда x − γ параллелен N , или, что то же самое, тогда и только тогда, когда x = γ + λ N для некоторого λ ∈ R . Следует, что

${\displaystyle L_{t_{0}}:=\{{\mathbf {x} }\in \mathbb {R} ^{2}:F(t_{0},{\mathbf {x} })=0\}}$

это в точности нормальная линия к γ в точке γ( t ₀ ). Чтобы найти дискриминант F, нам нужно вычислить его частную производную по t :

${\displaystyle {\frac {\partial F}{\partial t}}(t,{\mathbf {x} })=\kappa (t)({\mathbf {x} }-\gamma (t))\cdot {\mathbf {N} }(t)-1\ ,}$

где κ — кривизна плоской кривой γ. Было замечено, что F = 0 тогда и только тогда, когда x - γ = λ N для некоторого λ ∈ R . Предполагая, что F = 0, получим

${\displaystyle {\frac {\partial F}{\partial t}}=\lambda \kappa (t)-1\ .}$

Предполагая, что κ ≠ 0, отсюда следует, что λ = 1/κ и, следовательно,

${\displaystyle {\mathcal {D}}=\gamma (t)+{\frac {1}{\kappa (t)}}{\mathbf {N} }(t)\ .}$

Это и есть эволюта кривой γ.

Пример 4

Астроида как оболочка семейства линий, соединяющих точки ( s ^, 0), ​​(0, t ) с s2  +  t2  = ¹

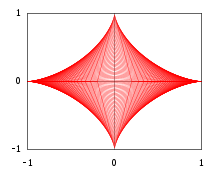
Следующий пример показывает, что в некоторых случаях оболочку семейства кривых можно рассматривать как топологическую границу объединения множеств, границами которых являются кривые оболочки. Для и рассмотрим (разомкнутый) прямоугольный треугольник в декартовой плоскости с вершинами , и ${\displaystyle s>0}$ ${\displaystyle t>0}$ ${\displaystyle (0,0)}$ ${\displaystyle (s,0)}$ ${\displaystyle (0,t)}$

${\displaystyle T_{s,t}:=\left\{(x,y)\in \mathbb {R} _{+}^{2}:\ {\frac {x}{s}}+{\frac {y}{t}}<1\right\}.}$

Зафиксируйте показатель степени и рассмотрите объединение всех треугольников, на которые наложено ограничение , то есть открытое множество. ${\displaystyle \alpha >0}$ ${\displaystyle T_{s,t}}$ ${\displaystyle \textstyle s^{\alpha }+t^{\alpha }=1}$

${\displaystyle \Delta _{\alpha }:=\bigcup _{s^{\alpha }+t^{\alpha }=1}T_{s,t}.}$

Чтобы написать декартово представление для , начните с любого , удовлетворяющего и любого . Неравенство Гёльдера относительно сопряженных показателей дает : ${\displaystyle \textstyle \Delta _{\alpha }}$ ${\displaystyle \textstyle s>0}$ ${\displaystyle \textstyle t>0}$ ${\displaystyle \textstyle s^{\alpha }+t^{\alpha }=1}$ ${\displaystyle \textstyle (x,y)\in \mathbb {R} _{+}^{2}}$ ${\displaystyle \textstyle \mathbb {R} ^{2}}$ ${\displaystyle p:=1+{\frac {1}{\alpha }}}$ ${\displaystyle \textstyle q:={1+\alpha }}$

${\displaystyle x^{\frac {\alpha }{\alpha +1}}+y^{\frac {\alpha }{\alpha +1}}\leq \left({\frac {x}{s}}+{\frac {y}{t}}\right)^{\frac {\alpha }{\alpha +1}}{\Big (}s^{\alpha }+t^{\alpha }{\Big )}^{\frac {1}{\alpha +1}}=\left({\frac {x}{s}}+{\frac {y}{t}}\right)^{\frac {\alpha }{\alpha +1}}}$,

с равенством тогда и только тогда, когда . В терминах объединения множеств последнее неравенство гласит: точка принадлежит множеству , то есть она принадлежит некоторому с тогда и только тогда, когда она удовлетворяет ${\displaystyle \textstyle s:\,t=x^{\frac {1}{1+\alpha }}:\,y^{\frac {1}{1+\alpha }}}$ ${\displaystyle (x,y)\in \mathbb {R} _{+}^{2}}$ ${\displaystyle \textstyle \Delta _{\alpha }}$ ${\displaystyle \textstyle T_{s,t}}$ ${\displaystyle \textstyle s^{\alpha }+t^{\alpha }=1}$

${\displaystyle x^{\frac {\alpha }{\alpha +1}}+y^{\frac {\alpha }{\alpha +1}}<1.}$

При этом граница множества является огибающей соответствующего семейства отрезков ${\displaystyle \mathbb {R} _{+}^{2}}$ ${\displaystyle \textstyle \Delta _{\alpha }}$

${\displaystyle \left\{(x,y)\in \mathbb {R} _{+}^{2}:\ {\frac {x}{s}}+{\frac {y}{t}}=1\right\}\ ,\qquad s^{\alpha }+t^{\alpha }=1}$

(то есть гипотенузы треугольников) и имеет декартово уравнение

${\displaystyle x^{\frac {\alpha }{\alpha +1}}+y^{\frac {\alpha }{\alpha +1}}=1.}$

Обратите внимание, что, в частности, значение дает дугу параболы из примера 2, а значение (означающее, что все гипотенузы являются сегментами единичной длины) дает астроиду . ${\displaystyle \alpha =1}$ ${\displaystyle \alpha =2}$

Пример 5

Огибающая орбит снарядов (с постоянной начальной скоростью) представляет собой вогнутую параболу. Начальная скорость 10 м/с. Примем g = 10 м/с ² .

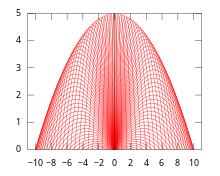
Мы рассмотрим следующий пример конверта в движении. Предположим, что на начальной высоте 0 в воздух бросается снаряд с постоянной начальной скоростью v , но с разными углами возвышения θ. Пусть x — горизонтальная ось поверхности движения, а y — вертикальная ось. Тогда движение дает следующую дифференциальную динамическую систему :

${\displaystyle {\frac {d^{2}y}{dt^{2}}}=-g,\;{\frac {d^{2}x}{dt^{2}}}=0,}$

который удовлетворяет четырем начальным условиям :

${\displaystyle {\frac {dx}{dt}}{\bigg |}_{t=0}=v\cos \theta ,\;{\frac {dy}{dt}}{\bigg |}_{t=0}=v\sin \theta ,\;x{\bigg |}_{t=0}=y{\bigg |}_{t=0}=0.}$

Здесь t обозначает время движения, θ — угол места, g — ускорение свободного падения , а v — постоянная начальная скорость (не скорость ). Решение приведенной выше системы может принять неявную форму :

${\displaystyle F(x,y,\theta )=x\tan \theta -{\frac {gx^{2}}{2v^{2}\cos ^{2}\theta }}-y=0.}$

Чтобы найти его уравнение огибающей, можно вычислить искомую производную:

${\displaystyle {\frac {\partial F}{\partial \theta }}={\frac {x}{\cos ^{2}\theta }}-{\frac {gx^{2}\tan \theta }{v^{2}\cos ^{2}\theta }}=0.}$

Исключив θ, можно получить следующее уравнение огибающей:

${\displaystyle y={\frac {v^{2}}{2g}}-{\frac {g}{2v^{2}}}x^{2}.}$

Очевидно, что полученная оболочка также является вогнутой параболой .

Конверт семейства поверхностей

Однопараметрическое семейство поверхностей в трехмерном евклидовом пространстве задается системой уравнений

${\displaystyle F(x,y,z,a)=0}$

в зависимости от реального параметра a . ^[2] Например, такое семейство образуют касательные плоскости к поверхности вдоль кривой на поверхности.

Две поверхности, соответствующие разным значениям a и a', пересекаются по общей кривой, определяемой формулой

${\displaystyle F(x,y,z,a)=0,\,\,{F(x,y,z,a^{\prime })-F(x,y,z,a) \over a^{\prime }-a}=0.}$

В пределе, когда а' приближается к а , эта кривая стремится к кривой, содержащейся на поверхности в точке а.

${\displaystyle F(x,y,z,a)=0,\,\,{\partial F \over \partial a}(x,y,z,a)=0.}$

Эта кривая называется характеристикой семейства при а . При изменении а геометрическое положение этих характеристических кривых определяет поверхность, называемую оболочкой семейства поверхностей.

Огибающая семейства поверхностей касается каждой поверхности в семействе вдоль характеристической кривой этой поверхности.

Обобщения

Идея оболочки семейства гладких подмногообразий вытекает естественным образом. В общем, если у нас есть семейство подмногообразий с коразмерностью c , то нам нужно иметь хотя бы семейство таких подмногообразий с параметром c . Например: однопараметрическое семейство кривых в трехмерном пространстве ( c = 2) вообще не имеет огибающей.

Приложения

Обыкновенные дифференциальные уравнения

Конверты связаны с изучением обыкновенных дифференциальных уравнений (ОДУ) и, в частности, сингулярных решений ОДУ. ^[3] Рассмотрим, например, однопараметрическое семейство касательных к параболе y = x ² . Они задаются порождающим семейством F ( t ,( x , y )) = t ² – 2 tx + y . Множество нулевого уровня F ( t ₀ ,( x , y )) = 0 дает уравнение касательной к параболе в точке ( t ₀ , t ₀ ² ). Уравнение t ² – 2 tx + y = 0 всегда можно решить относительно y как функции x , поэтому рассмотрим

${\displaystyle t^{2}-2tx+y(x)=0.\ }$

Замена

${\displaystyle t=\left({\frac {dy}{dx}}\right)/2}$

дает ОДУ

${\displaystyle \left({\frac {dy}{dx}}\right)^{2}\!\!-4x{\frac {dy}{dx}}+4y=0.}$

Неудивительно, что все y  = 2 tx  −  t ² являются решениями этого ОДУ. Однако огибающая этого однопараметрического семейства линий, которая представляет собой параболу y  =  x ² , также является решением этого ОДУ. Другой известный пример — уравнение Клеро .

Уравнения в частных производных

Конверты можно использовать для построения более сложных решений уравнений в частных производных (ЧДУ) первого порядка из более простых. ^[4] Пусть F ( x , u ,D u ) = 0 — УЧП первого порядка, где x — переменная со значениями в открытом множестве Ω ⊂  ^Rn , u — неизвестная вещественная функция, D u — градиент u , а F — непрерывно дифференцируемая функция, регулярная в D u . Предположим, что u ( x ; a ) — m -параметрическое семейство решений: то есть для каждого фиксированного a  ∈  A  ⊂  R ^m , u ( x ; a ) является решением дифференциального уравнения. Новое решение дифференциального уравнения можно построить, сначала решив (если возможно)

${\displaystyle D_{a}u(x;a)=0\,}$

для a  = φ( x ) как функции x . Огибающая семейства функций { u (·, a )} _{a ∈ A} определяется формулой

${\displaystyle v(x)=u(x;\varphi (x)),\quad x\in \Omega ,}$

а также решает дифференциальное уравнение (при условии, что оно существует как непрерывно дифференцируемая функция).

Геометрически график v ( x ) всюду касается графика некоторого члена семейства u ( x ; a ). Поскольку дифференциальное уравнение имеет первый порядок, оно ставит условие только на касательную плоскость к графику, так что любая функция, касающаяся решения везде, также должна быть решением. Эта же идея лежит в основе решения уравнения первого порядка как интеграла от конуса Монжа . ^[5] Конус Монжа — это поле конуса в R ^{n +1} переменных ( x , u ), вырезанное огибающей касательных пространств к УЧП первого порядка в каждой точке. Тогда решением УЧП является огибающая конусного поля.

В римановой геометрии , если гладкое семейство геодезических , проходящих через точку P в римановом многообразии, имеет огибающую, то P имеет сопряженную точку , в которой любая геодезическая семейства пересекает оболочку. То же самое верно и в более общем плане для вариационного исчисления : если семейство экстремалей функционала, проходящего через данную точку P , имеет огибающую, то точка, в которой экстремаль пересекает огибающую, является точкой, сопряженной с P.

Каустика

Светоотражающая каустика, созданная из круга и параллельных лучей

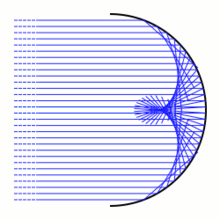
В геометрической оптике каустика — оболочка семейства световых лучей . На этой картинке изображена дуга круга. Лучи света (показаны синим цветом) исходят от источника, находящегося на бесконечности , и поэтому приходят параллельно. При попадании на дугу окружности лучи света рассеиваются в разные стороны по закону отражения . Когда луч света попадает на дугу в определенной точке, свет будет отражаться так, как если бы он был отражен касательной линией дуги в этой точке. Отраженные световые лучи дают на плоскости однопараметрическое семейство линий. Огибающая этих линий — отражающая каустика . Отражающая каустика обычно состоит из гладких точек и обычных точек возврата.

С точки зрения вариационного исчисления принцип Ферма (в его современной форме) означает, что световые лучи являются экстремалями функционала длины

${\displaystyle L[\gamma ]=\int _{a}^{b}|\gamma '(t)|\,dt}$

среди гладких кривых γ на [ a , b ] с фиксированными концами γ( a ) и γ( b ). Каустика, определяемая данной точкой P (на изображении точка находится на бесконечности), представляет собой множество точек, сопряженных с P . ^[6]

Принцип Гюйгенса

Свет может проходить через анизотропные неоднородные среды с разной скоростью в зависимости от направления и начального положения светового луча. Граница множества точек, в которые свет может пройти из данной точки q через время t , известна как волновой фронт после времени t , обозначенный здесь Φ _q ( t ). Он состоит именно из точек, до которых можно добраться из q за время t , путешествуя со скоростью света. Принцип Гюйгенса утверждает, что множество волновых фронтов Φ _{q 0} ( s + t ) является огибающей семейства волновых фронтов Φ _q ( s ) для q  ∈ Φ _{q 0} ( t ). В более общем смысле точку q ₀ можно заменить любой кривой, поверхностью или замкнутым множеством в пространстве. ^[7]

Смотрите также

• Каустик (математика)
• Теорема о конверте
• Линейчатая поверхность

Рекомендации

1. Брюс, JW; Гиблин, П.Дж. (1984), Кривые и особенности , издательство Кембриджского университета, ISBN 0-521-42999-4
2. Эйзенхарт, Лютер П. (2008), Трактат о дифференциальной геометрии кривых и поверхностей , Schwarz Press, ISBN 1-4437-3160-9
3. Форсайт, Эндрю Рассел (1959), Теория дифференциальных уравнений , Шесть томов в трех переплетах, Нью-Йорк: Dover Publications , MR  0123757, §§100-106.
4. Эванс, Лоуренс К. (1998), Уравнения в частных производных , Провиденс, Род-Айленд: Американское математическое общество , ISBN 978-0-8218-0772-9.
5. Джон, Фриц (1991), Уравнения в частных производных (4-е изд.), Springer, ISBN 978-0-387-90609-6.
6. Борн, Макс (октябрь 1999 г.), Принцип оптики , Cambridge University Press , ISBN 978-0-521-64222-4, Приложение I: Вариационное исчисление.
7. Арнольд, VI (1997), Математические методы классической механики, 2-е изд. , Берлин, Нью-Йорк: Springer-Verlag , ISBN 978-0-387-96890-2, §46.

Внешние ссылки

• Вайсштейн, Эрик В. «Конверт». Математический мир .
• «Конверт семейства плоских кривых» в MathCurve.