проблема джипа

Математическая задача размещения складов горючего

График зависимости количества топлива f от расстояния от начала координат d для исследования (1–3) и пересечения (I–III) версий задачи о джипе для трех единиц топлива – цветные стрелки обозначают склады, диагональные отрезки обозначают перемещение, а вертикальные отрезки обозначают перемещение топлива

Задача джипа ^[1] , задача пересечения пустыни ^[2] или задача исследования ^[3] — это математическая задача, в которой джип должен максимизировать расстояние, которое он может проехать в пустыне с заданным количеством топлива. Джип может перевозить только фиксированное и ограниченное количество топлива, но он может оставлять топливо и собирать его на топливных свалках в любой точке пустыни.

Задача впервые появилась в сборнике Propositiones ad Acuendos Juvenes ( Проблемы для оттачивания ума молодых ), приписываемом Алкуину , в котором речь шла о путешествующем верблюде, поедающем зерно. ^{[4] В труде} Луки Пачоли De viribus quantitatis (около 1500 г.) также обсуждается эта задача. Современное толкование было дано Н. Дж. Файном в 1947 г. ^[1]

Проблема

Постройте в масштабе версии задачи о джипе Exploring (вверху) и Crossing (внизу) для трех единиц топлива. Горизонтальная ось обозначает расстояние, а вертикальная ось обозначает время. Вертикальные цветные отрезки обозначают запасенное топливо, а горизонтальные — перемещение с использованием изъятого топлива. Цветные числа обозначают запасенные в данный момент единицы топлива.

На фиксированной базе хранится n единиц топлива. Джип может перевозить не более 1 единицы топлива в любой момент времени и может проехать 1 единицу расстояния на 1 единице топлива (предполагается, что расход топлива джипа постоянен). В любой момент поездки джип может оставить любое количество топлива, которое он перевозит, на свалке или может забрать любое количество топлива, которое было оставлено на свалке в предыдущей поездке, при условии, что его загрузка топлива никогда не превысит 1 единицы. Есть два варианта задачи:

• Исследование пустыни  — джип должен возвращаться на базу в конце каждой поездки.
• Пересечение пустыни  — джип должен возвращаться на базу в конце каждой поездки, за исключением последней поездки, когда джип проезжает как можно большее расстояние, прежде чем у него закончится топливо.

В любом случае цель состоит в том, чтобы максимизировать расстояние, пройденное джипом в его последней поездке. В качестве альтернативы, цель может заключаться в том, чтобы найти наименьшее количество топлива, требуемое для осуществления последней поездки на заданное расстояние.

Вариации

В классической задаче топливо в джипе и на свалках рассматривается как непрерывное количество. Были предложены более сложные вариации задачи, в которых топливо можно оставлять или собирать только дискретными количествами. ^[5]

Решение

Решение варианта «исследования пустыни» для n  = 3, показывающее запас топлива в джипе и топливные склады в начале каждой поездки и в точке поворота в каждой поездке.

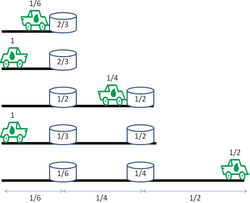
Стратегия, которая максимизирует расстояние, пройденное в последнем путешествии для варианта «исследование пустыни», выглядит следующим образом:

• Джип совершает n поездок. В каждой поездке он стартует с базы с 1 единицей топлива.
• В первой поездке джип проезжает расстояние в 1/(2 n ) единиц и оставляет ( n  − 1)/ n единиц топлива на топливной свалке. У джипа все еще остается 1/(2 n ) единиц топлива — как раз достаточно, чтобы вернуться на базу.
• В каждой из последующих n  − 1 поездок джип собирает 1/(2 n ) единиц топлива из этой первой топливной свалки по пути туда, так что он покидает топливную свалку, неся 1 единицу топлива. Он также собирает 1/(2 n ) единиц топлива из этой первой топливной свалки по пути обратно, что как раз достаточно для возвращения на базу.
• Во время второй поездки джип едет к первой топливной свалке и заправляется. Затем он проезжает расстояние в 1/(2 n  − 2) единиц и оставляет ( n  − 2)/( n  − 1) единиц топлива на второй топливной свалке. У джипа все еще есть 1/(2 n  − 2) единиц топлива, чего как раз достаточно, чтобы вернуться к первой топливной свалке. Здесь он собирает 1/(2 n ) единиц топлива, чего как раз достаточно, чтобы вернуться на базу.
• В каждой из последующих n  − 2 поездок джип собирает 1/(2 n  − 2) единиц топлива из этой второй топливной свалки по пути туда, так что он покидает топливную свалку, имея 1 единицу топлива. Он также собирает 1/(2 n  − 2) единиц топлива из второй топливной свалки по пути обратно, что как раз достаточно для возвращения к первой топливной свалке.
• Джип продолжает движение таким образом, так что в поездке k он устанавливает новую k -ю топливную свалку на расстоянии 1/(2 n  − 2 k  + 2) единиц от предыдущей топливной свалки и оставляет там ( n  −  k )/( n  −  k  + 1) единиц топлива. В каждой из последующих n  −  k поездок он собирает 1/(2 n  − 2 k  + 2) единиц топлива с k -й свалки по пути туда и еще 1/(2 n  − 2 k  + 2) единиц топлива по пути обратно.

Когда джип отправляется в последний рейс, есть n  − 1 топливных свалок. Самая дальняя содержит 1/2 единицы топлива, следующая дальняя содержит 1/3 единицы топлива и так далее, а ближайшая топливная свалка имеет всего 1/ n единиц топлива. Вместе с 1 единицей топлива, с которой он отправляется с базы, это означает, что джип может проехать общее расстояние туда и обратно

${\displaystyle 1+{\frac {1}{2}}+{\frac {1}{3}}+\cdots +{\frac {1}{n}}=\sum _{k=1}^{n}{\frac {1}{k}}\equiv 2\times \mathrm {explore} (n)}$

единиц в его последнем путешествии (максимальное расстояние, пройденное в пустыне, составляет половину этого). ^[3] Он собирает половину оставшегося топлива на каждой свалке по пути обратно, что заполняет его бак. Покинув самую дальнюю свалку, он проходит на 1/2 единицы дальше в пустыню, а затем возвращается к самой дальней свалке. Он собирает оставшееся топливо с каждой свалки по пути обратно, чего как раз достаточно, чтобы добраться до следующей свалки или, на последнем этапе, вернуться на базу.

Решение варианта «пересечения пустыни» для n  = 3, показывающее запас топлива в джипе и топливные склады в начале каждой поездки, в точке поворота в первых двух поездках и в конце последней поездки.

Расстояние, пройденное в последнем путешествии, — это n- ое гармоническое число , H _n . Поскольку гармонические числа не ограничены, можно превысить любое заданное расстояние в последнем путешествии, если на базе достаточно топлива. Однако количество требуемого топлива и количество сбросов топлива увеличиваются экспоненциально с расстоянием, которое необходимо преодолеть.

Вариант «пересечения пустыни» можно решить с помощью похожей стратегии, за исключением того, что теперь нет необходимости собирать топливо на обратном пути в последнем путешествии. Таким образом, в путешествии k джип устанавливает новый k -й топливный склад на расстоянии 1/(2 n  − 2 k  + 1) единиц от предыдущего топливного склада и оставляет там (2 n  − 2 k  − 1)/(2 n  − 2 k  + 1) единиц топлива. В каждой из следующих n  −  k  − 1 поездок он собирает 1/(2 n  − 2 k  + 1) единиц топлива с k -го склада по пути туда и еще 1/(2 n  − 2 k  + 1) единиц топлива по пути обратно.

Теперь, когда джип начинает свою последнюю поездку, есть n  − 1 топливных свалок. Самая дальняя содержит 1/3 единицы топлива, следующая дальняя содержит 1/5 единицы топлива и так далее, а ближайшая топливная свалка имеет всего 1/(2 n  − 1) единиц топлива. Вместе с 1 единицей топлива, с которой он стартует с базы, это означает, что джип может проехать общее расстояние

${\displaystyle 1+{\frac {1}{3}}+{\frac {1}{5}}+\cdots +{\frac {1}{2n-1}}=\sum _{k=1}^{n}{\frac {1}{2k-1}}=H_{2n-1}-{\frac {1}{2}}H_{n-1}\equiv \mathrm {cross} (n)}$

единиц в своем последнем путешествии. ^{[1] [3]} Он собирает все оставшееся топливо на каждой свалке по пути, заполняя свой бак. После того, как он покинул самую дальнюю свалку, он проезжает еще 1 единицу.

С

${\displaystyle \mathrm {cross} (n)=\sum _{k=1}^{n}{\frac {1}{2k-1}}>\sum _{k=1}^{n}{\frac {1}{2k}}={\frac {1}{2}}H_{n}=\mathrm {explore} (n)}$,

теоретически возможно пересечь пустыню любого размера, имея достаточно топлива на базе. Как и прежде, количество требуемого топлива и количество топливных свалок увеличиваются экспоненциально с расстоянием, которое необходимо преодолеть.

Подводя итог, можно сказать, что максимальное расстояние, которое может преодолеть джип (с запасом топлива на 1 единицу расстояния в любой момент времени) за n поездок (с n-1 заправками на полпути и общим потреблением n единиц топлива), составляет

• ${\displaystyle \mathrm {explore} (n)={\frac {1}{2}}H_{n}={\frac {1}{2}}+{\frac {1}{4}}+{\frac {1}{6}}+\cdots +{\frac {1}{2n}}}$, для исследования пустыни, где джип должен возвращаться на базу в конце каждой поездки;
• ${\displaystyle \mathrm {cross} (n)=H_{2n-1}-{\frac {1}{2}}H_{n-1}=1+{\frac {1}{3}}+{\frac {1}{5}}+\cdots +{\frac {1}{2n-1}}}$, для пересечения пустыни, где джип должен возвращаться на базу в конце каждой поездки, за исключением последней поездки, когда джип проезжает столько, сколько может, прежде чем у него закончится топливо.

Здесь находится номер n-й гармоники . ${\displaystyle H_{n}=1+{\frac {1}{2}}+{\frac {1}{3}}+\cdots +{\frac {1}{n}}}$

Постоянное количество топлива

Количество единиц топлива, доступных на базе, не обязательно должно быть целым числом. В общем случае максимальное расстояние, достижимое для задачи «исследовать пустыню» с n единицами топлива, равно

${\displaystyle \mathrm {explore} (n)=\int _{0}^{n}{\frac {\mathrm {d} f}{2\lceil n-f\rceil }}}$

причем первый топливный склад расположен на расстоянии единиц от стартовой базы, второй — на расстоянии единиц от первого топливного склада, третий — на расстоянии единиц от второго топливного склада и т. д. Здесь — дробная часть n . ${\displaystyle \{n\}/(2\lceil n\rceil )}$ ${\displaystyle 1/(2\lceil n\rceil -2)}$ ${\displaystyle 1/(2\lceil n\rceil -4)}$ ${\displaystyle \{n\}=n-\lfloor n\rfloor }$

Максимальное расстояние, которое можно преодолеть в задаче «пересечь пустыню» с n единицами топлива, равно

${\displaystyle \mathrm {cross} (n)=\int _{0}^{n}{\frac {\mathrm {d} f}{2\lceil n-f\rceil -1}}}$

причем первый топливный склад расположен на расстоянии единиц от стартовой базы, второй — на расстоянии единиц от первого топливного склада, третий — на расстоянии единиц от второго топливного склада и т. д. Здесь — дробная часть n . ${\displaystyle \{n\}/(2\lceil n\rceil -1)}$ ${\displaystyle 1/(2\lceil n\rceil -3)}$ ${\displaystyle 1/(2\lceil n\rceil -5)}$ ${\displaystyle \{n\}=n-\lfloor n\rfloor }$

независимость порядка

Порядок поездок джипа не фиксирован. Например, в версии задачи «исследование пустыни» джип может сделать n − 1 круговых поездок между базой и первым топливным складом, оставляя ( n − 1) / n единиц топлива на топливном складе каждый раз, а затем совершить n -ную поездку в одну сторону к первому топливному складу, таким образом прибыв туда с общим запасом ( n − 1) + 1/(2 n ) единиц топлива. 1/(2 n ) единиц сохраняются для обратного пути на базу в самом конце, а остальные n − 1 единиц топлива используются для перемещения топлива между первым и вторым топливными складами, используя n − 2 круговых поездок, а затем ( n −1) -ную поездку в одну сторону ко второму топливному складу. И так далее.

Практические применения

В ходе операции Black Buck One атакующий Vulcan дозаправлялся семь раз на пути туда и один раз на обратном пути. Серые линии обозначают резервные самолеты для замены потерь.

Проблема может иметь практическое применение в военных ситуациях, особенно в отношении эффективности использования топлива . В контексте бомбардировки Японии во Второй мировой войне бомбардировщиками B-29 Роберт Макнамара в фильме «Туман войны» говорит , что понимание проблемы эффективности использования топлива, вызванной необходимостью транспортировки топлива на передовые базы, было главной причиной, по которой стратегия бомбардировок с материкового Китая была отвергнута в пользу стратегии « прыжков с острова на остров» :

«Нам пришлось переправить эти самолеты с баз в Канзасе в Индию. Затем нам пришлось переправить топливо через горб в Китай. [...] Мы должны были взять эти B-29 — там не было самолетов-заправщиков . Мы должны были заправить их топливом, вылететь из Индии в Чэнду , выгрузить топливо, вернуться в Индию, выполнить достаточно миссий, чтобы накопить топливо в Чэнду, вылететь в Явату , Япония , разбомбить сталелитейные заводы и вернуться в Индию. У нас было так мало подготовки по этой проблеме максимизации [топливной] эффективности, что мы фактически обнаружили, что вместо того, чтобы выгружать топливо, им пришлось его забрать. Короче говоря, это не стоило ни гроша. И именно Лемей пришел к такому выводу и заставил Чифов перенести все это на Марианские острова , что опустошило Японию». ^[6]

( В конце Второй мировой войны операции по атомной бомбардировке осуществлялись с использованием бомбардировщиков B-29 Superfortress с тихоокеанского острова Тиниан в составе Северных Марианских островов .)

Смотрите также

• Прочитайте Operation Black Buck , чтобы лучше понять применение этих идей. В этих миссиях, проведенных во время Фолклендской войны , Королевские ВВС использовали дозаправку в воздухе, размещая танкеры, чтобы бомбардировщики Vulcan, базирующиеся на острове Вознесения, могли бомбить цели на Фолклендских островах .
• Гармонический ряд (математика)
• Оптимизация (математика)

Ссылки

1. Weisstein, Eric W. «Проблема джипа». MathWorld .
2. Гарднер, Мартин (1994). Мои лучшие математические и логические головоломки . Дувр. стр. 53. ISBN 0-486-28152-3.
3. " Проблемы исследования. Другой распространенный вопрос касается максимального расстояния в пустыне, на которое может проникнуть из пограничного поселения исследователь, способный нести провизию, которой ему хватит на несколько дней". WW Rouse Ball и HSM Coxeter (1987). Mathematical Recreations and Essays , тринадцатое издание, Дувр, стр. 32. ISBN 0-486-25357-0 . 
4. Задачи для оттачивания мастерства молодых, Джон Хэдли и Дэвид Сингмастер, The Mathematical Gazette , 76 , № 475 (март 1992 г.), стр. 102–126.
5. Оптимальная логистика для экспедиций: проблема джипа с полной заправкой, Гюнтер Роте и Гочуань Чжан, июнь 1996 г.
6. Стенограмма «Тумана войны», www.errolmorris.com