Парадокс Гиббса

Мысленный эксперимент по статистической физике

В статистической механике полуклассический вывод энтропии , не учитывающий неразличимость частиц, дает выражение для энтропии, которое не является экстенсивным (не пропорционально количеству рассматриваемого вещества). Это приводит к парадоксу , известному как парадокс Гиббса , в честь Джозайи Уилларда Гиббса , который предложил этот мысленный эксперимент в 1874–1875 годах. ^{[1] [2]} Парадокс позволяет энтропии закрытых систем уменьшаться, нарушая второй закон термодинамики . Связанный с этим парадокс - это «парадокс смешивания». Если принять точку зрения, что определение энтропии необходимо изменить, чтобы игнорировать перестановку частиц, в термодинамическом пределе парадокс можно избежать.

Иллюстрация проблемы

Сам Гиббс рассматривал следующую проблему, которая возникает, если энтропия идеального газа не является экстенсивной. ^[1] Два одинаковых контейнера с идеальным газом стоят рядом. Газ в контейнере №1 во всех отношениях идентичен газу в контейнере №2 (т.е. по объему, массе, температуре, давлению и т.д.). С каждым контейнером связана определенная энтропия S , которая зависит от объема каждого контейнера. Теперь дверь в стенке контейнера открывается, чтобы позволить частицам газа смешиваться между контейнерами. Никаких макроскопических изменений не происходит, поскольку система находится в равновесии. Энтропию газа в системе с двумя контейнерами можно легко вычислить, но если уравнение не является расширенным, энтропия не будет равна 2 S . Фактически, неэкстенсивная величина энтропии, определенная и изученная Гиббсом, могла бы предсказать дополнительную энтропию. Затем закрытие двери снова снижает энтропию до S на коробку, что является предполагаемым нарушением Второго закона термодинамики .

Как это понял Гиббс ^[2] и недавно вновь подчеркнул ^{[3] [4]} , это неправильное применение неэкстенсивной величины энтропии Гиббса. Если частицы газа различимы, закрытие дверей не вернет систему в исходное состояние – у многих частиц окажутся переключенные контейнеры. В том, что определяется как упорядоченное, существует свобода, и было бы ошибкой заключить, что энтропия не увеличилась. В частности, неэкстенсивная величина энтропии Гиббса для идеального газа не предназначалась для изменения числа частиц.

Парадокс можно предотвратить, сделав вывод о неразличимости (по крайней мере, эффективной неразличимости) частиц в объеме. В результате получается обширное уравнение Сакура – ​​Тетрода для энтропии, полученное следующим образом.

Вычислить энтропию идеального газа и сделать ее обширной

В классической механике состояние идеального газа с энергией U , объемом V и с N частицами, каждая частица имеет массу m , представляется путем указания вектора импульса p и вектора положения x для каждой частицы. Это можно рассматривать как указание точки в 6 N -мерном фазовом пространстве , где каждая из осей соответствует одной из координат импульса или положения одной из частиц. Набор точек в фазовом пространстве, которые может занимать газ, определяется ограничением того, что газ будет иметь определенную энергию:

${\displaystyle U={\frac {1}{2m}}\sum _{i=1}^{N}(p_{ix}^{2}+p_{iy}^{2}+p_{iz}^{2})}$

и содержаться внутри объема V (скажем, V — куб со стороной X, так что V = X ³ ):

${\displaystyle 0\leq x_{ij}\leq X}$

для и ${\displaystyle i=1...N}$ ${\displaystyle j=1,2,3}$

Первое ограничение определяет поверхность 3N-мерной гиперсферы радиуса (2 mU ) ^{1/2, а} второе представляет собой 3N - мерный гиперкуб объемом VN . Они объединяются, образуя 6N - мерный гиперцилиндр. Подобно тому, как площадь стенки цилиндра равна произведению окружности основания на высоту, так и площадь стенки φ этого гиперцилиндра равна:

${\displaystyle \phi (U,V,N)=V^{N}\left({\frac {2\pi ^{\frac {3N}{2}}(2mU)^{\frac {3N-1}{2}}}{\Gamma (3N/2)}}\right)~~~~~~~~~~~(1)}$

Энтропия пропорциональна логарифму числа состояний, которые может иметь газ при соблюдении этих ограничений. В классической физике число состояний бесконечно велико, но согласно квантовой механике оно конечно. До появления квантовой механики эта бесконечность была регуляризована путем дискретизации фазового пространства. Фазовое пространство было разделено на блоки объёмом h ^{3 N} . Таким образом, константа h появилась в результате математического трюка и считалась не имеющей физического значения. Однако, используя квантовую механику, можно восстановить тот же формализм в квазиклассическом пределе, но теперь с h , являющимся постоянной Планка. Качественно это можно увидеть на примере принципа неопределенности Гейзенберга ; объем в фазовом пространстве N меньше h ^{3 N} ( h — постоянная Планка) указать нельзя.

Чтобы вычислить количество состояний, мы должны вычислить объем фазового пространства, в котором может находиться система, и разделить его на h ^{3 N} . Это приводит нас к другой проблеме: кажется, что объем приближается к нулю, поскольку область фазового пространства, в которой может находиться система, представляет собой область нулевой толщины. Эта проблема является результатом задания энергии U с бесконечной точностью. В общей системе без симметрий полная квантовая трактовка привела бы к дискретному невырожденному набору собственных энергетических состояний. Точная спецификация энергии затем зафиксирует точное состояние, в котором находится система, поэтому число состояний, доступных системе, будет равно одному, а энтропия, таким образом, будет равна нулю.

Когда мы определяем внутреннюю энергию как U , мы на самом деле имеем в виду , что полная энергия газа находится где-то в интервале длины вокруг U. Здесь взято очень малое, оказывается, что энтропия не сильно зависит от выбора при больших N . Это означает, что указанная выше «площадь» φ должна быть расширена до оболочки толщиной, равной неопределенности импульса , поэтому энтропия определяется выражением: ${\displaystyle \delta U}$ ${\displaystyle \delta U}$ ${\displaystyle \delta U}$ ${\displaystyle \delta p=\delta \left({\sqrt {2mU}}\right)={\sqrt {\frac {m}{2U}}}\delta U}$

${\displaystyle \left.\right.S=k\,\ln(\phi \delta p/h^{3N})}$

где константа пропорциональности равна k , константе Больцмана . Используя приближение Стирлинга для гамма-функции , в котором отсутствуют члены меньше порядка N , энтропия для больших N становится:

${\displaystyle S=kN\ln \left[V\left({\frac {U}{N}}\right)^{\frac {3}{2}}\right]+{\frac {3}{2}}kN\left(1+\ln {\frac {4\pi m}{3h^{2}}}\right)}$

Эта величина невелика, как можно увидеть, рассматривая два идентичных объема с одинаковым числом частиц и одинаковой энергией. Предположим, что два тома вначале разделены барьером. Удаление или повторная установка стены обратима, но энтропия увеличивается при удалении барьера на величину

${\displaystyle \delta S=k\left[2N\ln(2V)-N\ln V-N\ln V\right]=2kN\ln 2>0}$

что противоречит термодинамике, если вы снова вставите барьер. Это парадокс Гиббса.

Парадокс разрешается постулированием того, что частицы газа на самом деле неразличимы. Это означает, что все состояния, отличающиеся только перестановкой частиц, следует считать одним и тем же состоянием. Например, если у нас есть газ, состоящий из двух частиц, и мы указываем AB как состояние газа, в котором первая частица ( A ) имеет импульс p ₁ , а вторая частица ( B ) имеет импульс p ₂ , то это состояние, а также состояние BA , в котором частица B имеет импульс p ₁ , а частица A имеет импульс p _2, следует считать одним и тем же состоянием.

Для газа N -частиц существует N ! состояния, которые в этом смысле идентичны, если предположить, что каждая частица находится в различном одночастичном состоянии. Можно смело сделать это предположение при условии, что газ не имеет чрезвычайно высокой плотности. Таким образом, в нормальных условиях можно рассчитать объем фазового пространства, занимаемого газом, разделив уравнение 1 на N !. Снова используя приближение Стирлинга для больших N , ln( N !) ≈ N ln( N ) − N , энтропия для больших N равна:

${\displaystyle S=kN\ln \left[\left({\frac {V}{N}}\right)\left({\frac {U}{N}}\right)^{\frac {3}{2}}\right]+kN\left({\frac {5}{2}}+{\frac {3}{2}}\ln {\frac {4\pi m}{3h^{2}}}\right)}$

легко показать, что оно обширно. Это уравнение Сакура–Тетроде .

Парадокс смешивания

Тесно связанным с парадоксом Гиббса парадоксом является парадокс смешивания . Парадокс Гиббса — это частный случай «парадокса смешивания», который содержит все его существенные особенности. Разница в том, что парадокс смешивания имеет дело с произвольными различиями в двух газах, а не только с различиями в порядке частиц, как считал Гиббс. В этом смысле это прямое обобщение аргумента Гиббса. Снова возьмем ящик с перегородкой, в котором с одной стороны находится газ А, с другой стороны — газ Б, причем оба газа имеют одинаковые температуру и давление. Если газы A и B — разные газы, при смешивании газов возникает энтропия. Если газы одинаковые, дополнительная энтропия не рассчитывается. Дополнительная энтропия от смешения не зависит от характера газов; это зависит только от того, что газы разные. Два газа могут быть сколь угодно похожими, но энтропия от смешивания не исчезает, если они не являются одним и тем же газом – парадоксальный разрыв.

Этот «парадокс» можно объяснить, внимательно рассмотрев определение энтропии. В частности, как кратко объяснил Эдвин Томпсон Джейнс ^[2] , определения энтропии произвольны.

Как указывает центральный пример в статье Джейнса, можно разработать теорию, которая рассматривает два газа как одинаковые, даже если на самом деле эти газы можно различить посредством достаточно детальных измерений. Пока мы не проведем эти детальные измерения, теория не будет иметь внутренних противоречий. (Другими словами, не имеет значения, что мы называем газы A и B одним и тем же именем, если мы еще не обнаружили, что они различны.) Если наша теория называет газы A и B одинаковыми, то энтропия не изменится, когда мы смешать их. Если наша теория называет газы A и B разными, то энтропия действительно увеличивается при их смешивании. Это понимание предполагает, что идеи «термодинамического состояния» и «энтропии» несколько субъективны.

Дифференциальное увеличение энтропии ( dS ) в результате смешивания разнородных газов, умноженное на температуру ( T ), равно минимальному количеству работы, которое мы должны совершить, чтобы вернуть газы в исходное разделенное состояние. Предположим, что два газа различны, но мы не можем обнаружить их различия. Если эти газы находятся в ящике, отделенном друг от друга перегородкой, сколько работы потребуется для восстановления исходного состояния системы после того, как мы удалим перегородку и дадим газам перемешаться?

Нет – просто вставьте раздел заново. Несмотря на то, что газы смешались, в системе никогда не наблюдалось заметного изменения состояния, поскольку по гипотезе газы экспериментально неразличимы.

Как только мы сможем различить разницу между газами, работа, необходимая для восстановления макроскопической конфигурации предварительного смешивания из состояния после смешивания, становится ненулевой. Этот объем работы зависит не от того, насколько различны газы, а только от того, различимы ли они.

Эта линия рассуждений особенно информативна при рассмотрении представлений о неразличимых частицах и правильном счете Больцмана . Первоначальное выражение Больцмана для числа состояний, доступных газу, предполагало, что состояние может быть выражено через ряд энергетических «подуровней», каждый из которых содержит определенное количество частиц. В то время как частицы на данном подуровне считались неотличимыми друг от друга, частицы на разных подуровнях считались отличимыми от частиц на любом другом подуровне. Это равносильно утверждению, что обмен двумя частицами на двух разных подуровнях приведет к заметно различному «обменному макросостоянию» газа. Например, если мы рассмотрим простой газ с N частицами, с достаточно низкой плотностью, так что практически наверняка каждый подуровень содержит либо одну частицу, либо ни одной (т. е. газ Максвелла-Больцмана), это означает, что простой контейнер с газом будет в одном из N ! заметно разные «обменные макросостояния», по одному на каждый возможный обмен частицами.

Подобно тому, как парадокс смешивания начинается с двух заметно разных контейнеров, а дополнительная энтропия, возникающая при смешивании, пропорциональна среднему объему работы, необходимой для восстановления этого исходного состояния после смешивания, так и дополнительная энтропия в исходном выводе Больцмана пропорциональна средней величине объем работы, необходимый для восстановления простого газа из некоторого «обменного макросостояния» в исходное «обменное макросостояние». Если мы предположим, что на самом деле не существует экспериментально обнаруживаемой разницы в этих «обменных макросостояниях», то использование энтропии, возникающей в результате предположения о неразличимости частиц, даст непротиворечивую теорию. Это «правильный подсчет Больцмана».

Часто говорят, что разрешение парадокса Гиббса связано с тем фактом, что, согласно квантовой теории, подобные частицы в принципе неразличимы. По рассуждениям Джейнса, если частицы экспериментально неразличимы по какой-либо причине, парадокс Гиббса разрешается, и квантовая механика лишь дает гарантию того, что в квантовой сфере эта неразличимость будет истинной как вопрос принципа, а не обусловлена ​​каким-либо принципом. недостаточно отточенный экспериментальный потенциал.

Нерасширенная энтропия двух идеальных газов и как ее исправить

В этом разделе мы в общих чертах представляем чисто классический вывод неэкстенсивной энтропии для идеального газа, рассмотренный Гиббсом до учета «правильного счета» (неразличимости частиц). Далее следует краткое обсуждение двух стандартных методов увеличения энтропии. Наконец, мы представляем третий метод, предложенный Р. Свендсеном, для обширного (аддитивного) результата для энтропии двух систем, если им разрешено обмениваться частицами друг с другом. ^{[5] [6]}

Настраивать

Приведем упрощенный вариант расчета. Он отличается от полного расчета тремя способами:

1. Идеальный газ состоит из частиц, ограниченных одним пространственным измерением.
2. Мы сохраняем только члены порядка , отбрасывая все члены размера n или меньше, где n — количество частиц. Для наших целей этого достаточно, потому что именно здесь проявляется парадокс Гиббса и именно здесь он должен быть разрешен. Пренебрегаемые члены играют роль, когда число частиц не очень велико, например, в компьютерном моделировании и нанотехнологиях . Также они необходимы при выводе уравнения Сакура–Тетроде . ${\displaystyle n\log(n)}$
3. Деление фазового пространства на единицы постоянной Планка ( h ) опущено. Вместо этого энтропия определяется с помощью интеграла по «доступной» части фазового пространства. Это подчеркивает чисто классический характер расчета.

Начнем с версии энтропии Больцмана , в которой подынтегральная функция представляет собой все доступное фазовое пространство :

${\displaystyle S=k\ln \Omega =k\ln \oint \limits _{H({\vec {p}},{\vec {q}})=E}(d{\vec {p}}\,)^{n}(d{\vec {q}}\,)^{n}}$

Интеграл ограничен контуром доступных областей фазового пространства, при условии сохранения энергии. В отличие от одномерных линейных интегралов, встречающихся в элементарной физике, контур постоянной энергии обладает огромным числом измерений. Обоснование интегрирования по фазовому пространству с использованием канонической меры предполагает предположение о равной вероятности. Это предположение можно сделать, привлекая эргодическую гипотезу , а также теорему Лиувилля о гамильтоновых системах.

(Эргодическая гипотеза лежит в основе способности физической системы достигать теплового равновесия , но это не всегда справедливо для компьютерного моделирования (см. проблему Ферми-Пасты-Улама-Цингу ) или в некоторых реальных системах, таких как нетепловая плазма. .)

Теорема Лиувилля предполагает фиксированное количество измерений, которые «исследует» система. При расчетах энтропии размерность числа пропорциональна количеству частиц в системе, что заставляет фазовое пространство резко менять размерность при добавлении или вычитании частиц. Этим можно объяснить трудности построения наглядного и простого вывода зависимости энтропии от числа частиц.

Для идеального газа доступным фазовым пространством является ( n - 1)-сфера (также называемая гиперсферой) в n -мерном пространстве: ${\displaystyle {\vec {v}}}$

${\displaystyle E=\sum _{j=1}^{n}{\frac {1}{2}}mv_{j}^{2}\,,}$

Чтобы восстановить парадоксальный результат о том, что энтропия не является экстенсивной, мы интегрируем по фазовому пространству газ одноатомных частиц , ограниченных одним пространственным измерением посредством . Поскольку наша единственная цель — пролить свет на парадокс, мы упростим обозначения, приняв массу частицы и постоянную Больцмана равными единице: . Мы представляем точки в фазовом пространстве и его части x и v n и 2 n размерными векторами: ${\displaystyle n}$ ${\displaystyle 0<x<\ell }$ ${\displaystyle m=k=1}$

${\displaystyle {\vec {\xi }}=[x_{1},...,x_{n},v_{1},...,v_{n}]=[{\vec {x}},{\vec {v}}\,]}$   где     и   ${\displaystyle {\vec {x}}=[x_{1},...,x_{n}]}$ ${\displaystyle {\vec {v}}=[v_{1},...,v_{n}]\,.}$

Для расчета энтропии мы используем тот факт, что (n-1)-сфера имеет ( n - 1) -мерный «гиперповерхностный объем» ${\displaystyle \Sigma v_{j}^{2}=R^{2}\,,}$

${\displaystyle {\tilde {A}}_{n}(R)={\frac {n\pi ^{n/2}}{(n/2)!}}R^{n-1}\,.}$

Например, если n = 2, 1-сфера — это круг , «гиперповерхность» на плоскости. Когда сфера четномерная ( n нечетная), необходимо будет использовать гамма-функцию , чтобы придать смысл факториалу; см. ниже. ${\displaystyle {\tilde {A}}_{2}(R)=2\pi R}$

Парадокс Гиббса в одномерном газе

Парадокс Гиббса возникает, когда энтропия рассчитывается с использованием размерного фазового пространства, где также находится число частиц в газе. Эти частицы пространственно ограничены одномерным интервалом . Объем поверхности фиксированной энергии равен ${\displaystyle n}$ ${\displaystyle n}$ ${\displaystyle \ell ^{n}}$

${\displaystyle \Omega _{E,\ell }=\left(\int dx_{1}\int dx_{2}...\int dx_{n}\right)\left(\underbrace {\int dv_{1}\int dv_{2}...\int dv_{n}} _{\Sigma v_{i}^{2}=2E}\right)}$

Нижние индексы используются для определения «переменных состояния» и будут обсуждаться позже, когда будет доказано, что число частиц не имеет полного статуса в качестве переменной состояния в этом расчете. Интеграл по конфигурационному пространству равен . Как указано нижней фигурной скобкой, интеграл по пространству скоростей ограничен «площадью поверхности» n - 1- мерной гиперсферы радиуса и, следовательно, равен «площади» этой гиперповерхности. Таким образом ${\displaystyle \Omega }$ ${\displaystyle n}$ ${\displaystyle \ell ^{n}}$ ${\displaystyle {\sqrt {2E}}}$

${\displaystyle \Omega _{E,\ell }=\ell ^{n}{\frac {n\pi ^{n/2}}{(n/2)!}}(2E)^{\frac {n-1}{2}}}$

После аппроксимации факториала и отбрасывания малых членов получаем

${\displaystyle {\begin{aligned}\ln \Omega _{E,\ell }&\approx n\ln \ell +n\ln {\sqrt {\frac {E}{n}}}+{\text{const.}}\\&=\underbrace {n\ln {\frac {\ell }{n}}+n\ln {\sqrt {\frac {E}{n}}}} _{\text{extensive}}+\,n\ln n+{\text{const.}}\\\end{aligned}}}$

Во втором выражении член вычитали и добавляли, используя тот факт, что . Это было сделано для того, чтобы подчеркнуть, что определенная здесь «энтропия» не может быть обширным свойством материи. Первые два слагаемых обширны: если объем системы увеличивается в два раза, но заполняется одинаковой плотностью частиц с одинаковой энергией, то каждое из этих слагаемых увеличивается вдвое. Но третий термин не является ни экстенсивным, ни интенсивным и поэтому неверен. ${\displaystyle n\ln n}$ ${\displaystyle \ln \ell -\ln n=\ln(\ell /n)}$

Произвольная константа была добавлена ​​потому, что энтропию обычно можно рассматривать как определенную с точностью до произвольной аддитивной константы. Это особенно необходимо, когда энтропия определяется как логарифм объема фазового пространства, измеряемый в единицах импульса-положения. Любое изменение в определении этих единиц приведет к добавлению или вычитанию константы из значения энтропии.

Два стандартных способа сделать классическую энтропию обширной

Как обсуждалось выше, экстенсивная форма энтропии восстанавливается, если мы разделим объем фазового пространства , на n !. Альтернативный подход состоит в том, чтобы утверждать, что зависимости от числа частиц нельзя доверять на том основании, что изменение также меняет размерность фазового пространства. Такие изменения размерности выходят за рамки гамильтоновой механики и теоремы Лиувилля . По этой причине вполне вероятно, что произвольная константа будет функцией . ^[7] Определив функцию как , мы имеем: ${\displaystyle \Omega _{E,\ell }}$ ${\displaystyle n}$ ${\displaystyle n}$ ${\displaystyle f(n)=-{\frac {3}{2}}n\ln n}$

${\displaystyle {\begin{aligned}S=\ln \Omega _{E,\ell }&\approx n\ln \ell +n\ln {\sqrt {E}}+{\text{const.}}\\&=n\ln \ell +n\ln {\sqrt {E}}+f(n)\\\ln \Omega _{E,\ell ,n}&\approx n\ln {\frac {\ell }{n}}+n\ln {\sqrt {\frac {E}{n}}}+{\text{const.}},\\\end{aligned}}}$

который имеет обширное масштабирование:

${\displaystyle S(\alpha E,\alpha \ell ,\alpha n)=\alpha \,S(E,\ell ,n)}$

Подход Свендсена к обмену частицами

Следуя Свендсену ^{[5] [6]} , мы позволяем двум системам обмениваться частицами. По сути, это «освобождает место» в фазовом пространстве для входа или выхода частиц, не требуя изменения количества измерений фазового пространства. Общее количество частиц : ${\displaystyle N}$

• ${\displaystyle n_{A}}$частицы имеют координаты . ${\displaystyle 0<x<\ell _{A}}$

  Полная энергия этих частиц равна ${\displaystyle E_{A}}$

• ${\displaystyle n_{B}}$частицы имеют координаты . ${\displaystyle 0<x<\ell _{B}}$

  Полная энергия этих частиц равна ${\displaystyle E_{B}}$

• Система подвержена ограничениям и ${\displaystyle E_{A}+E_{B}=E}$ ${\displaystyle n_{A}+n_{B}=N}$

Интегрируя по фазовому пространству, имеем:

${\displaystyle {\begin{aligned}\Omega _{E,\ell ,N}&=\left(\underbrace {\int dx_{?}...\int dx_{?}} _{n_{A}\;{\text{terms}}}\underbrace {\int dx_{?}...\int dx_{N}} _{n_{B}\;{\text{terms}}}\right)\left(\underbrace {\int dv_{1}\int dv_{2}...\int dv_{N}} _{\Sigma v^{2}=2E_{A}\;{\text{or}}\;\Sigma v^{2}=2E_{B}}\right)\\&=\left(\ell _{A}\right)^{n_{A}}\left(\ell _{B}\right)^{n_{B}}\left(\underbrace {\frac {N!}{n_{A}!n_{B}!}} _{\text{combination}}\right)\left(\underbrace {{\frac {n_{A}\pi ^{n_{A}/2}}{(n_{A}/2)!}}(2E_{A})^{\frac {n_{A}-1}{2}}} _{n_{A}-{\text{sphere}}}\right)\left(\underbrace {{\frac {n_{B}\pi ^{n_{B}/2}}{(n_{B}/2)!}}(2E_{B})^{\frac {n_{B}-1}{2}}} _{n_{B}-{\text{sphere}}}\right)\end{aligned}}}$

Знаки вопроса (?) служат напоминанием о том, что мы не можем предполагать, что первые n A _частиц (т. е. от 1 до n _A ) находятся в системе A , в то время как другие частицы ( от n _B до N ) находятся в системе B. (Подробнее об этом говорится в следующем разделе.)

Логарифмируя и оставляя только самые большие члены, мы имеем:

$${\displaystyle S=\ln \Omega _{E,\ell ,N}\approx n_{A}\ln \left({\frac {n_{A}}{\ell _{A}}}{\sqrt {\frac {E_{A}}{\ell _{A}}}}\right)+n_{B}\ln \left({\frac {n_{B}}{\ell _{B}}}{\sqrt {\frac {E_{B}}{\ell _{B}}}}\right)+N\ln N+{\text{const.}}}$$

Это можно интерпретировать как сумму энтропии системы A и системы B , обеих экстенсивных. И есть термин, который не является обширным. ${\displaystyle N\ln N}$

Визуализация подхода обмена частицами в трех измерениях

Трехчастичный идеальный газ, разделенный на две части.

Правильные (обширные) формулы для систем A и B были получены благодаря тому, что мы включили все возможные способы обмена частицами между двумя системами. Использование комбинаций (т.е. N частиц выбирают N _A ) использовалось для определения числа способов разделения N частиц на систему A , содержащую n _A частиц, и систему B , содержащую n _B частиц. Этот расчет оправдан не физическими соображениями, а необходимостью интегрирования по фазовому пространству. Как будет показано ниже, фазовое пространство содержит не одну n _A -сферу и одну n _B -сферу, а вместо этого

${\displaystyle {N \choose n_{A}}={\frac {N!}{n_{A}!n_{B}!}}}$

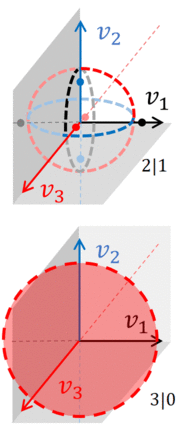
пары n -сфер, расположенных в одном и том же ( N + 1) -мерном пространстве скоростей. Интеграл по доступному фазовому пространству должен включать все эти n -сферы, как видно на рисунке, который показывает фактическое фазовое пространство скоростей, связанное с газом, состоящим из трех частиц. Более того, этот газ разделился на две системы : А и В.

Если пренебречь пространственными переменными, то фазовое пространство газа с тремя частицами является трехмерным, что позволяет нарисовать n -сфер , по которым необходимо взять интеграл по фазовому пространству. Если все три частицы находятся вместе, соотношение между двумя газами составляет 3|0. Доступное фазовое пространство ограничено обычной сферой ( 2-сферой ) с радиусом либо или (в зависимости от того, в какой системе находятся частицы). ${\displaystyle {\sqrt {2E_{1}}}}$ ${\displaystyle {\sqrt {2E_{2}}}}$

Если расщепление равно 2|1, то фазовое пространство состоит из кругов и точек . Каждый круг занимает два измерения, и для каждого круга две точки лежат на третьей оси, равноудаленные от центра круга. Другими словами, если система A имеет 2 частицы, доступное фазовое пространство состоит из 3 пар n -сфер , каждая пара представляет собой 1-сферу и 0-сферу :

${\displaystyle v_{1}^{2}+v_{2}^{2}=2E_{A}\qquad v_{3}^{2}=2E_{B}}$

${\displaystyle v_{2}^{2}+v_{3}^{2}=2E_{A}\qquad v_{1}^{2}=2E_{B}}$

${\displaystyle v_{3}^{2}+v_{1}^{2}=2E_{A}\qquad v_{2}^{2}=2E_{B}}$

Обратите внимание, что

${\displaystyle {3 \choose 2}=3.}$

Рекомендации

1. Гиббс, Дж. Уиллард (1875–1878). О равновесии гетерогенных веществ . Коннектикут Акад. наук. ISBN 0-8493-9685-9.Перепечатано в Gibbs, J. Willard (октябрь 1993 г.). Научные статьи Дж. Уилларда Гиббса (Том 1) . Пресс для лука быка. ISBN 0-918024-77-3. и у Гиббса, Дж. Уилларда (февраль 1994 г.). Научные статьи Дж. Уилларда Гиббса (Том 2) . Пресс для лука быка. ISBN 1-881987-06-Х.
2. Джейнс, Эдвин Т. (1996). «Парадокс Гиббса» (PDF) . Проверено 8 ноября 2005 г.
3. Град, Гарольд (1961). «Многоликая энтропия». Сообщения по чистой и прикладной математике . 14 (3): 323–354. дои : 10.1002/cpa.3160140312.
4. ван Кампен, НГ (1984). «Парадокс Гиббса». В МЫ Пэрри (ред.). Очерки по теоретической физике в честь Дирка тер Хаара . Оксфорд: Пергамон. ISBN 978-0080265230.
5. Свендсен, Роберт (март 2006 г.). «Статистическая механика коллоидов и определение энтропии Больцмана». Американский журнал физики . 74 (3): 187–190. Бибкод : 2006AmJPh..74..187S. дои : 10.1119/1.2174962.
6. Свендсен, Роберт Х. (июнь 2002 г.). «Статистическая механика классических систем с различимыми частицами». Журнал статистической физики . 107 (5/6): 1143–1166. Бибкод : 2002JSP...107.1143S. дои : 10.1023/А: 1015161825292. S2CID  122463989.
7. Джейнс, ET (1992). Парадокс Гиббса в максимальной энтропии и байесовских методах (под редакцией Ч.Р. Смита, Г.Дж. Эриксона и П.О. Нойдорфера) (PDF) . Дордрехт, Голландия: Kluwer Academic Publishers. стр. 1–22. В частности, Гиббс не смог указать, что «константа интегрирования» — это не произвольная константа, а произвольная функция. Но это имеет, как мы увидим, нетривиальные физические последствия. Примечательно не то, что Гиббс не смог подчеркнуть тонкий математический момент почти в последних написанных им словах; но в течение 80 лет после этого все авторы учебников (за исключением, возможно, Паули) не смогли этого увидеть.

дальнейшее чтение

• Чи-Юань Ценг и Ариэль Катича (2001). «Еще одно разрешение парадокса Гиббса: подход теории информации». В Р. Л. Фрае (ред.). Байесовский вывод и методы максимальной энтропии в науке и технике . Материалы конференции AIP. Том. 617. с. 331. arXiv : cond-mat/0109324 . дои : 10.1063/1.1477057.
• Дикс, Деннис (2011). «Возвращение к парадоксу Гиббса». В Деннисе Диксе; Венсеслао Х. Гонсалес; Стефан Хартманн ; Томас Юбель; Марсель Вебер (ред.). Объяснение, предсказание и подтверждение . Философия науки в европейской перспективе. стр. 367–377. arXiv : 1003.0179 . дои : 10.1007/978-94-007-1180-8_25. ISBN 978-94-007-1179-2. S2CID  118395415.

Внешние ссылки

• Парадокс Гиббса и его решения - различные сборники статей.