Константа связи

Параметр, описывающий величину силы

В физике константа связи или параметр калибровочной связи (или, проще говоря, связь ) — это число, определяющее величину силы, действующей при взаимодействии . Первоначально константа связи связывала силу, действующую между двумя статическими телами, с « зарядами » тел (то есть электрическим зарядом для электростатики и массой для ньютоновской гравитации ), деленными на квадрат расстояния, между телами; таким образом: в для ньютоновской гравитации и в для электростатики . Это описание остается справедливым в современной физике для линейных теорий со статическими телами и безмассовыми носителями силы . ^{[ требуется ссылка ]} ${\displaystyle r^{2}}$ ${\displaystyle G}$ ${\displaystyle F=Gm_{1}m_{2}/r^{2}}$ ${\displaystyle k_{\text{e}}}$ ${\displaystyle F=k_{\text{e}}q_{1}q_{2}/r^{2}}$

Современное и более общее определение использует лагранжиан (или, что эквивалентно, гамильтониан ) системы. Обычно, (или ) системы, описывающей взаимодействие, можно разделить на кинетическую часть и часть взаимодействия : (или ). В теории поля всегда содержит 3 или более полевых термина, выражая, например, что начальный электрон (поле 1) взаимодействует с фотоном (поле 2), создавая конечное состояние электрона (поле 3). Напротив, кинетическая часть всегда содержит только два поля, выражая свободное распространение начальной частицы (поле 1) в более позднее состояние (поле 2). Константа связи определяет величину части относительно части (или между двумя секторами части взаимодействия, если присутствуют несколько полей, которые связываются по-разному). Например, электрический заряд частицы является константой связи, которая характеризует взаимодействие с двумя полями, несущими заряд, и одним полем фотона (отсюда общая диаграмма Фейнмана с двумя стрелками и одной волнистой линией). Поскольку фотоны опосредуют электромагнитную силу, эта связь определяет, насколько сильно электроны чувствуют такую ​​силу, и ее значение фиксируется экспериментом. Рассматривая лагранжиан КЭД , можно увидеть, что действительно, связь устанавливает пропорциональность между кинетическим членом и членом взаимодействия . ${\displaystyle {\mathcal {L}}}$ ${\displaystyle {\mathcal {H}}}$ ${\displaystyle {\mathcal {L}}}$ ${\displaystyle {\mathcal {H}}}$ ${\displaystyle T}$ ${\displaystyle V}$ ${\displaystyle {\mathcal {L}}=T-V}$ ${\displaystyle {\mathcal {H}}=T+V}$ ${\displaystyle V}$ ${\displaystyle T}$ ${\displaystyle T}$ ${\displaystyle V}$ ${\displaystyle T={\bar {\psi }}(i\hbar c\gamma ^{\sigma }\partial _{\sigma }-mc^{2})\psi -{1 \over 4\mu _{0}}F_{\mu \nu }F^{\mu \nu }}$ ${\displaystyle V=-e{\bar {\psi }}(\hbar c\gamma ^{\sigma }A_{\sigma })\psi }$

Связь играет важную роль в динамике. Например, часто устанавливают иерархии приближений, основанные на важности различных констант связи. При движении большого куска намагниченного железа магнитные силы могут быть важнее гравитационных сил из-за относительных величин констант связи. Однако в классической механике эти решения обычно принимаются напрямую путем сравнения сил. Другим важным примером центральной роли, которую играют константы связи, является то, что они являются параметрами расширения для первопринципных расчетов, основанных на теории возмущений , которая является основным методом расчета во многих разделах физики.

Постоянная тонкой структуры

Связи возникают естественным образом в квантовой теории поля . Особую роль в релятивистских квантовых теориях играют связи, которые безразмерны ; т.е. являются чистыми числами. Примером такой безразмерной константы является постоянная тонкой структуры ,

${\displaystyle \alpha ={\frac {e^{2}}{4\pi \varepsilon _{0}\hbar c}},}$

где e - заряд электрона , ε ₀ - диэлектрическая проницаемость свободного пространства , ħ - приведенная постоянная Планка , а c - скорость света . Эта константа пропорциональна квадрату силы связи заряда электрона с электромагнитным полем .

Муфта калибра

В неабелевой калибровочной теории параметр калибровочной связи , , появляется в лагранжиане как ${\displaystyle g}$

${\displaystyle {\frac {1}{4g^{2}}}{\rm {Tr}}\,G_{\mu \nu }G^{\mu \nu },}$

(где G — тензор калибровочного поля ) в некоторых соглашениях. В другом широко используемом соглашении G масштабируется так, что коэффициент кинетического члена равен 1/4 и появляется в ковариантной производной . Это следует понимать как нечто похожее на безразмерную версию элементарного заряда, определяемого как ${\displaystyle g}$

${\displaystyle {\frac {e}{\sqrt {\varepsilon _{0}\hbar c}}}={\sqrt {4\pi \alpha }}\approx 0.30282212\ ~~.}$

Слабая и сильная связь

В квантовой теории поля с константой связи g , если g намного меньше 1, говорят, что теория слабосвязанная . В этом случае она хорошо описывается разложением по степеням g , называемым теорией возмущений . Если константа связи имеет порядок один или больше, говорят, что теория сильносвязанная . Примером последнего является адронная теория сильных взаимодействий (именно поэтому она изначально называется сильной). В таком случае для исследования теории необходимо использовать непертурбативные методы.

В квантовой теории поля размерность связи играет важную роль в свойстве перенормируемости теории ^[1] и, следовательно, в применимости теории возмущений. Если связь безразмерна в системе естественных единиц (т. е . , ), как в КЭД, КХД и слабом взаимодействии , теория перенормируема, и все члены ряда разложения конечны (после перенормировки). Если связь размерна, как, например, в гравитации ( ), теории Ферми ( ) или киральной теории возмущений сильного взаимодействия ( ), то теория обычно не перенормируема. Разложения возмущений в связи все еще могут быть осуществимы, хотя и в рамках ограничений ^{[2] [3]} , поскольку большинство членов ряда более высокого порядка будут бесконечными. ${\displaystyle c=1}$ ${\displaystyle \hbar =1}$ ${\displaystyle [G_{N}]={\text{energy}}^{-2}}$ ${\displaystyle [G_{F}]={\text{energy}}^{-2}}$ ${\displaystyle [F]={\text{energy}}}$

Муфта ходовая

Рис. 1 Виртуальные частицы перенормируют связь

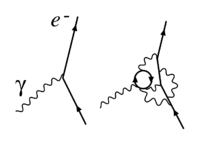
Можно исследовать квантовую теорию поля на коротких временах или расстояниях, изменяя длину волны или импульс, k , используемого зонда. С помощью высокочастотного (т.е. коротковременного) зонда можно увидеть виртуальные частицы, принимающие участие в каждом процессе. Это кажущееся нарушение закона сохранения энергии можно понять эвристически, исследуя соотношение неопределенности

${\displaystyle \Delta E\Delta t\geq {\frac {\hbar }{2}},}$

что фактически допускает такие нарушения на коротких временах. Вышеизложенное замечание относится только к некоторым формулировкам квантовой теории поля, в частности, каноническому квантованию в картине взаимодействия .

В других формулировках то же самое событие описывается «виртуальными» частицами, выходящими за пределы массовой оболочки . Такие процессы перенормируют связь и делают ее зависимой от масштаба энергии μ , на котором исследуется связь. Зависимость связи g ( μ ) от масштаба энергии известна как «прогон связи». Теория прогона связей задается группой перенормировки , хотя следует иметь в виду, что группа перенормировки является более общей концепцией, описывающей любые изменения масштаба в физической системе (подробности см. в полной статье).

Феноменология работы муфты

Группа перенормировки предоставляет формальный способ вывести работу связи, однако феноменологию, лежащую в основе этой работы, можно понять интуитивно. ^[4] Как объяснено во введении, константа связи задает величину силы, которая ведет себя с расстоянием как . Зависимость от - впервые была объяснена Фарадеем как уменьшение потока силы : в точке B , удаленной на от тела A, создающего силу, этот поток пропорционален потоку поля, проходящему через элементарную поверхность S, перпендикулярную линии AB . Поскольку поток равномерно распространяется в пространстве, он уменьшается в соответствии с телесным углом, поддерживающим поверхность S . В современном представлении квантовой теории поля происходит из выражения в пространстве положений пропагатора носителей силы . Для относительно слабо взаимодействующих тел, как это обычно бывает в электромагнетизме или гравитации или ядерных взаимодействиях на коротких расстояниях, обмен одним носителем силы является хорошим первым приближением взаимодействия между телами, и классически взаимодействие будет подчиняться -закону (обратите внимание, что если носитель силы массивен, существует дополнительная зависимость ). Когда взаимодействия более интенсивны (например, заряды или массы больше или меньше) или происходят в течение более коротких промежутков времени (меньше ), вовлекается больше носителей силы или создаются пары частиц , см. рис. 1, что приводит к нарушению поведения. Классический эквивалент заключается в том, что поток поля больше не распространяется свободно в пространстве, а, например, подвергается экранированию от зарядов дополнительных виртуальных частиц или взаимодействий между этими виртуальными частицами. Удобно отделить закон первого порядка от этой дополнительной -зависимости. Эта последняя затем учитывается путем включения в связь, которая затем становится -зависимой (или, что эквивалентно, μ -зависимой). Поскольку дополнительные частицы, вовлеченные за пределами приближения одного носителя силы, всегда являются виртуальными , т.е. представляют собой кратковременные квантовые флуктуации поля, становится понятно, почему протекание взаимодействия является подлинным квантовым и релятивистским явлением, а именно, эффектом диаграмм Фейнмана высокого порядка на величину силы. ${\displaystyle 1/r^{2}}$ ${\displaystyle 1/r^{2}}$ ${\displaystyle r}$ ${\displaystyle 1/r^{2}}$ ${\displaystyle 1/r^{2}}$ ${\displaystyle r}$ ${\displaystyle r}$ ${\displaystyle r}$ ${\displaystyle 1/r^{2}}$ ${\displaystyle 1/r^{2}}$ ${\displaystyle r}$ ${\displaystyle 1/r}$

Поскольку бегущая связь эффективно учитывает микроскопические квантовые эффекты, ее часто называют эффективной связью , в отличие от голой связи (константы), присутствующей в лагранжиане или гамильтониане.

Бета-функции

В квантовой теории поля бета - функция β ( g ) кодирует поведение параметра связи g . Она определяется соотношением

${\displaystyle \beta (g)=\mu {\frac {\partial g}{\partial \mu }}={\frac {\partial g}{\partial \ln \mu }},}$

где μ — масштаб энергии данного физического процесса. Если бета-функции квантовой теории поля равны нулю, то теория масштабно-инвариантна .

Параметры связи квантовой теории поля могут течь, даже если соответствующая классическая теория поля является масштабно-инвариантной . В этом случае ненулевая бета-функция говорит нам, что классическая масштабно-инвариантная является аномальной .

КЭД и полюс Ландау

Если бета-функция положительна, соответствующая связь увеличивается с ростом энергии. Примером является квантовая электродинамика (КЭД), где с помощью теории возмущений можно обнаружить , что бета-функция положительна. В частности, при низких энергиях α ≈ 1/137 , тогда как в масштабе Z-бозона , около 90  ГэВ , измеряется α ≈ 1/127 .

Более того, пертурбативная бета-функция говорит нам, что связь продолжает увеличиваться, и QED становится сильно связанной при высокой энергии. Фактически, связь, по-видимому, становится бесконечной при некоторой конечной энергии. Это явление было впервые отмечено Львом Ландау и называется полюсом Ландау . Однако нельзя ожидать, что пертурбативная бета-функция даст точные результаты при сильной связи, и поэтому вполне вероятно, что полюс Ландау является артефактом применения теории возмущений в ситуации, когда она больше не действительна. Истинное поведение масштабирования при больших энергиях неизвестно. ${\displaystyle \alpha }$

КХД и асимптотическая свобода

Сравнение измерений константы сильной связи в различных экспериментах по состоянию на 2023 год с ATLAS — последним и наиболее точным значением ^{[5] [6]}

В неабелевых калибровочных теориях бета-функция может быть отрицательной, как впервые обнаружили Фрэнк Вильчек , Дэвид Политцер и Дэвид Гросс . Примером этого является бета-функция для квантовой хромодинамики (КХД), и в результате связь КХД уменьшается при высоких энергиях. ^[4]

Более того, связь уменьшается логарифмически, явление, известное как асимптотическая свобода (открытие которой было отмечено Нобелевской премией по физике в 2004 году). Связь уменьшается примерно как

${\displaystyle \alpha _{\text{s}}(k^{2})\ {\stackrel {\mathrm {def} }{=}}\ {\frac {g_{\text{s}}^{2}(k^{2})}{4\pi }}\approx {\frac {1}{\beta _{0}\ln \left({k^{2}}/{\Lambda ^{2}}\right)}},}$

где — энергия процесса, а β ₀ — константа, впервые вычисленная Вильчеком, Гроссом и Политцером. ${\displaystyle k}$

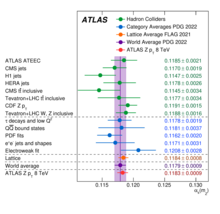
Наоборот, связь увеличивается с уменьшением энергии. Это означает, что связь становится большой при низких энергиях, и больше нельзя полагаться на теорию возмущений . Следовательно, фактическое значение константы связи определяется только в заданном масштабе энергии. В КХД обычно выбирается шкала масс Z-бозона, обеспечивающая значение константы сильной связи α _s (M _Z ² ) = 0,1179 ± 0,0010. ^[7] В 2023 году Atlas измерил α _s (M _Z ² ) = 0,1183 ± 0,0009, что является самым точным на сегодняшний день. ^{[5] [6]} Самые точные измерения получены в результате расчетов решеточной КХД, исследований распада тау-лептона, а также путем переинтерпретации спектра поперечного импульса Z-бозона. ^[8]

шкала КХД

В квантовой хромодинамике (КХД) величина Λ называется шкалой КХД . Значение равно ^[4] для трех «активных» ароматов кварков, а именно, когда энергия-импульс, участвующий в процессе, позволяет производить только верхние, нижние и странные кварки, но не более тяжелые кварки. Это соответствует энергиям ниже 1,275 ГэВ. При более высокой энергии Λ меньше, например, МэВ ^[9] выше массы нижнего кварка около 5  ГэВ . Значение минимальной шкалы схемы вычитания (MS) Λ _MS приведено в статье о размерной трансмутации . Отношение масс протона и электрона в первую очередь определяется шкалой КХД. ${\displaystyle \Lambda _{\rm {MS}}=332\pm 17{\text{ MeV}}}$ ${\displaystyle \Lambda _{\rm {MS}}=210\pm 14}$

Теория струн

Замечательно иная ситуация существует в теории струн, поскольку она включает дилатон . Анализ спектра струн показывает, что это поле должно присутствовать либо в бозонной струне , либо в секторе NS–NS суперструны . Используя вершинные операторы , можно увидеть, что возбуждение этого поля эквивалентно добавлению члена к действию, где скалярное поле связывается со скаляром Риччи . Таким образом, это поле представляет собой целую функцию, стоящую констант связи. Эти константы связи не являются предопределенными, регулируемыми или универсальными параметрами; они зависят от пространства и времени таким образом, который определяется динамически. Источники, которые описывают связь струн так, как если бы она была фиксированной, обычно ссылаются на значение вакуумного ожидания . Оно может иметь любое значение в бозонной теории, где нет суперпотенциала .

Смотрите также

• Каноническое квантование , перенормировка и размерная регуляризация
• Квантовая теория поля , в частности квантовая электродинамика и квантовая хромодинамика
• Глюонное поле , Тензор напряженности глюонного поля

Ссылки

1. Zee, A. (2010). Квантовая теория поля в двух словах (2-е изд.). Принстон, Нью-Джерси: Princeton University Press . ISBN 978-0691140346.
2. Leutwyler, Heinrich (2012). "Киральная теория возмущений". Scholarpedia . 7 (10): 8708. Bibcode :2012SchpJ...7.8708L. doi : 10.4249/scholarpedia.8708 .
3. Донохью, Джон Ф. (1995). «Введение в эффективное описание теории поля гравитации». В Корнете, Фернандо (ред.). Эффективные теории: Труды Высшей школы, Альмуньекар, Испания, 26 июня – 1 июля 1995 г. Сингапур: World Scientific . arXiv : gr-qc/9512024 . Bibcode : 1995gr.qc....12024D. ISBN 978-981-02-2908-5.
4. Deur, Alexandre; Brodsky, Stanley J.; De Téramond, Guy F. (2016). «Бегущая связь КХД». Progress in Particle and Nuclear Physics . 90 : 1–74. arXiv : 1604.08082 . Bibcode :2016PrPNP..90....1D. doi :10.1016/j.ppnp.2016.04.003. S2CID  118854278.
5. Сотрудничество ATLAS (2023). «Точное определение константы сильной связи из отдачи Z-бозонов с помощью эксперимента ATLAS при √ s = 8 ТэВ». arXiv : 2309.12986 [hep-ex].
6. "ATLAS измеряет силу сильного взаимодействия с рекордной точностью". ЦЕРН . 2023-10-11 . Получено 2023-10-24 .
7. Zyla, PA; et al. (Particle Data Group) (14 августа 2020 г.). "Обзор физики элементарных частиц – Глава 9. Квантовая хромодинамика" (PDF) . Progress of Theoretical and Experimental Physics . 2020 (8). doi : 10.1093/ptep/ptaa104 .
8. Камарда, Стефано; Феррера, Джанкарло; Шотт, Маттиас (2024). «Определение константы сильной связи из распределения поперечного импульса Z-бозона». The European Physical Journal C . 84 (1): 39. arXiv : 2203.05394 . Bibcode :2024EPJC...84...39C. doi : 10.1140/epjc/s10052-023-12373-2 .
9. Patrignani, C.; et al. (Particle Data Group) (октябрь 2016 г.). "Обзор физики элементарных частиц – Глава 9. Квантовая хромодинамика" (PDF) . Chinese Physics C . 40 (10): 100001. doi : 10.1088/1674-1137/40/10/100001 .

Внешние ссылки

• Нобелевская премия по физике 2004 года – Информация для общественности
• Факультет физики и астрономии Университета штата Джорджия – Константы связи для фундаментальных сил
• Введение в квантовую теорию поля, М.Е. Пескин и Х.Д. Шредер, ISBN 0-201-50397-2