
Поверхность потенциальной энергии ( ППЭ ) или энергетический ландшафт описывает энергию системы , особенно набора атомов, с точки зрения определенных параметров , обычно положений атомов. Поверхность может определять энергию как функцию одной или нескольких координат; если есть только одна координата, поверхность называется кривой потенциальной энергии или энергетическим профилем . Примером является потенциал Морзе/дальнобойности .
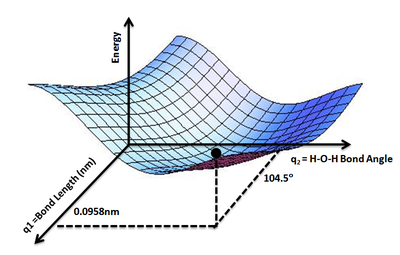
Полезно использовать аналогию с ландшафтом: для системы с двумя степенями свободы (например, двумя длинами связей) значение энергии (аналогия: высота земли) является функцией двух длин связей (аналогия: координаты положения на земле). [1]
Концепция PES находит применение в таких областях, как физика , химия и биохимия , особенно в теоретических подотраслях этих предметов. Она может использоваться для теоретического исследования свойств структур, состоящих из атомов, например, для нахождения минимальной энергетической формы молекулы или вычисления скоростей химической реакции . Она может использоваться для описания всех возможных конформаций молекулярной сущности или пространственных положений взаимодействующих молекул в системе, или параметров и соответствующих им уровней энергии, обычно свободной энергии Гиббса . Геометрически энергетический ландшафт представляет собой график энергетической функции в конфигурационном пространстве системы. Этот термин также используется в более общем смысле в геометрических перспективах математической оптимизации , когда областью определения функции потерь является пространство параметров некоторой системы.
Геометрия набора атомов может быть описана вектором r , элементы которого представляют положения атомов. Вектор r может быть набором декартовых координат атомов или также может быть набором межатомных расстояний и углов.
При заданном r энергия как функция положений, E ( r ) , является значением E ( r ) для всех интересующих r . Используя аналогию с ландшафтом из введения, E дает высоту на «энергетическом ландшафте», так что возникает концепция поверхности потенциальной энергии .
Для изучения химической реакции с использованием ППЭ как функции атомных позиций необходимо рассчитать энергию для каждого интересующего атомного расположения. Методы расчета энергии конкретного атомного расположения атомов хорошо описаны в статье по вычислительной химии , и здесь акцент будет сделан на поиске приближений E ( r ) для получения мелкозернистой информации об энергии и положении.
Для очень простых химических систем или когда делаются упрощающие приближения относительно межатомных взаимодействий, иногда можно использовать аналитически выведенное выражение для энергии как функции атомных положений. Примером является потенциал Лондона - Эйринга - Полани - Сато [2] [3] [4] для системы H + H 2 как функция трех расстояний HH.
Для более сложных систем расчет энергии конкретного расположения атомов часто оказывается слишком затратным в вычислительном отношении для крупномасштабных представлений поверхности, чтобы быть осуществимым. Для таких систем возможным подходом является расчет только сокращенного набора точек на ППЭ, а затем использование вычислительно более дешевого метода интерполяции, например, интерполяции Шепарда , для заполнения пробелов. [5]
ППЭ — это концептуальный инструмент для помощи в анализе молекулярной геометрии и динамики химических реакций . После того, как необходимые точки оценены на ППЭ, точки можно классифицировать в соответствии с первой и второй производными энергии по положению, которые соответственно являются градиентом и кривизной . Стационарные точки (или точки с нулевым градиентом) имеют физическое значение: минимумы энергии соответствуют физически стабильным химическим видам, а седловые точки соответствуют переходным состояниям , точке с самой высокой энергией на координате реакции (которая является путем с самой низкой энергией, соединяющим химический реагент с химическим продуктом).
Термин полезен при изучении сворачивания белка ; в то время как теоретически белок может существовать в почти бесконечном числе конформаций вдоль своего энергетического ландшафта, в реальности белки сворачиваются (или «расслабляются») во вторичные и третичные структуры , которые обладают минимально возможной свободной энергией . Ключевой концепцией подхода энергетического ландшафта к сворачиванию белка является гипотеза воронкообразной структуры .
В катализе при разработке новых катализаторов или усовершенствовании существующих энергетические ландшафты рассматриваются с целью избежания промежуточных продуктов с низкой или высокой энергией, которые могут остановить реакцию или потребовать чрезмерного количества энергии для получения конечных продуктов. [6]
В моделях остекления локальные минимумы энергетического ландшафта соответствуют метастабильным низкотемпературным состояниям термодинамической системы . [7] [8]
В машинном обучении искусственные нейронные сети могут быть проанализированы с использованием аналогичных подходов. [9] Например, нейронная сеть может быть в состоянии идеально соответствовать обучающему набору , соответствующему глобальному минимуму нулевых потерь, но переобучаться модели («изучая шум» или «запоминая обучающий набор»). Понимание того, когда это происходит, можно изучить с помощью геометрии соответствующего энергетического ландшафта. [10]
Потенциальные энергетические поверхности для химических реакций можно классифицировать как притягивающие или отталкивающие, сравнивая удлинения длин связей в активированном комплексе относительно удлинений длин связей в реагентах и продуктах. [11] [12] Для реакции типа A + B—C → A—B + C удлинение длины связи для вновь образованной связи A—B определяется как R* AB = R AB − R 0 AB , где R AB — длина связи A—B в переходном состоянии и R 0 AB в молекуле продукта. Аналогично для связи, которая разрывается в реакции, R* BC = R BC − R 0 BC , где R 0 BC относится к молекуле реагента. [13]
Для экзотермических реакций ППЭ классифицируется как привлекательная (или рано нисходящая ), если R* AB > R* BC , так что переходное состояние достигается, когда реагенты приближаются друг к другу. После переходного состояния длина связи A—B продолжает уменьшаться, так что большая часть высвобождаемой энергии реакции преобразуется в колебательную энергию связи A—B. [13] [14] Примером является реакция гарпуна K + Br 2 → K—Br + Br, в которой начальное дальнодействующее притяжение реагентов приводит к активированному комплексу, напоминающему K + •••Br − •••Br. [13] Колебательно-возбужденные популяции молекул продуктов можно обнаружить с помощью инфракрасной хемилюминесценции . [15] [16]
Напротив, ППЭ для реакции H + Cl 2 → HCl + Cl является отталкивающей (или поздненисходящей ), поскольку R* HCl < R* ClCl , а переходное состояние достигается, когда продукты разделяются. [13] [14] Для этой реакции, в которой атом A (здесь H) легче, чем B и C, энергия реакции выделяется в основном в виде поступательной кинетической энергии продуктов. [13] Для такой реакции, как F + H 2 → HF + H, в которой атом A тяжелее, чем B и C, происходит смешанное выделение энергии, как колебательное, так и поступательное, даже несмотря на то, что ППЭ является отталкивающей. [13]
Для эндотермических реакций тип поверхности определяет тип энергии, наиболее эффективный для осуществления реакции. Трансляционная энергия реагентов наиболее эффективна для инициирования реакций с притягивающей поверхностью, в то время как колебательное возбуждение (до более высокого колебательного квантового числа v) более эффективно для реакций с отталкивающей поверхностью. [13] В качестве примера последнего случая, реакция F + HCl(v=1) → Cl + HF примерно в пять раз быстрее, чем F + HCl(v=0) → Cl + HF для той же полной энергии HCl. [17]
Концепция поверхности потенциальной энергии для химических реакций была впервые предложена французским физиком Рене Марселином в 1913 году. [18] Первый полуэмпирический расчет поверхности потенциальной энергии был предложен для реакции H + H 2 Генри Эйрингом и Майклом Полани в 1931 году. Эйринг использовал поверхности потенциальной энергии для расчета констант скорости реакции в теории переходного состояния в 1935 году.
Поверхности потенциальной энергии обычно изображаются в виде трехмерных графиков, но их также можно представить в виде двумерных графиков, на которых развитие реакции отображается с помощью изоэнергетических линий. Коллинеарная система H + H 2 представляет собой простую реакцию, которая позволяет построить двумерную ППЭ простым и понятным способом. В этой реакции атом водорода (H) реагирует с молекулой дигидрогена (H 2 ), образуя новую связь с одним атомом молекулы, что, в свою очередь, разрывает связь исходной молекулы. Это обозначается как H a + H b –H c → H a –H b + H c . Прогресс реакции от реагентов (H + H₂) до продуктов (HHH), а также энергия видов, которые принимают участие в реакции, хорошо определены на соответствующей поверхности потенциальной энергии. Профили энергии описывают потенциальную энергию как функцию геометрических переменных (ППЭ в любом измерении не зависят от времени и температуры).

В 2-D PES имеются различные соответствующие элементы: